二项式定理
图片预览







文档简介
(共22张PPT)
高二数学课
二 项 式 定 理
问题:
(1)今天是星期一,那么7天后的这一天是星期几呢
(3)如果是 天后的这一天呢?
(2)如果是15天后的这一天呢?
(星期二)
(星期一)
回顾:
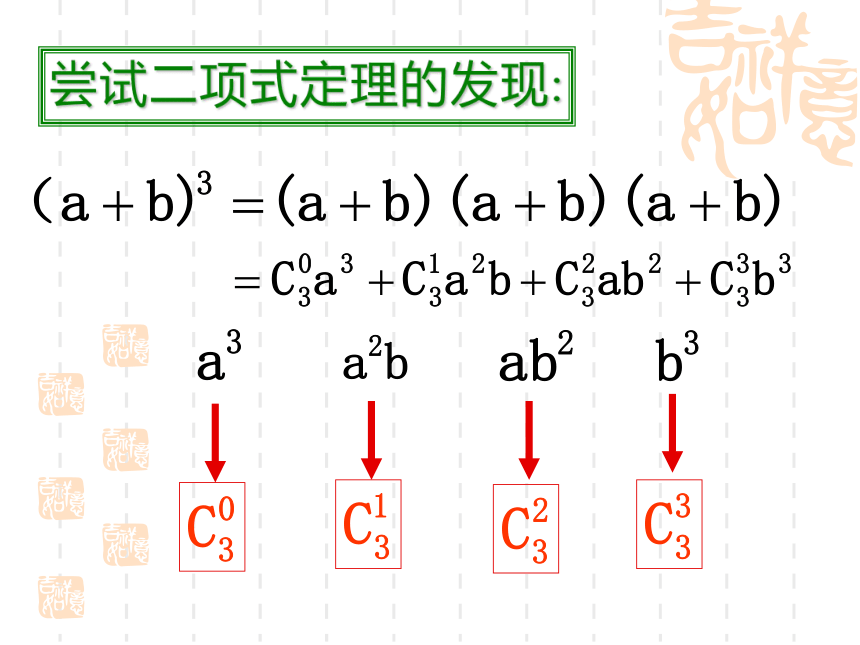
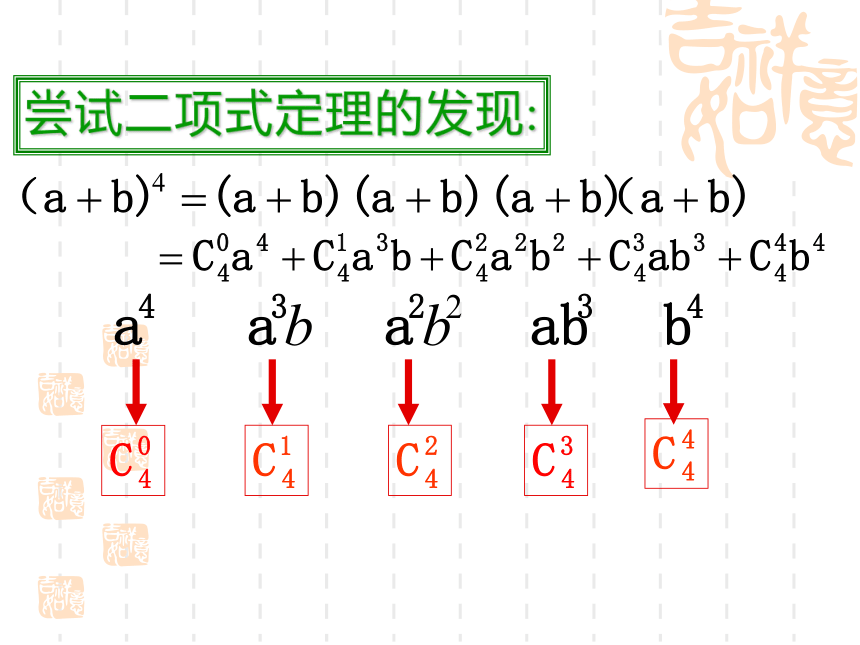
尝试二项式定理的发现:
尝试二项式定理的发现:
尝试二项式定理的发现:
发现规律:
对于(a+b)n=
的展开式中an-rbr的系数是在n个括号中,恰有r个括号中取b(其余括号中取a)的组合数 .那么,我们能不能写出(a+b)n的展开式?
将(a+b)n展开的结果又是怎样呢?
归纳提高
引出定理,总结特征
这个公式表示的定理叫做二项式定理,公式
右边的多项式叫做 (a+b) n的 ,
其中 (r=0,1,2,……,n)叫做 ,
叫做二项展开式的通项,用 Tr+1
表示,该项是指展开式的第 项,展开式共有_____个项.
展开式
二项式系数
r+1
n+1
二项式定理
2.系数规律:
2.指数规律:
(1)各项的次数均为n;即为n次齐次式
(2)a的次数由n逐次降到0,
b的次数由0逐次升到n.
1.项数规律:
展开式共有n+1个项
二项式定理
特别地:
1、把b用-b代替
(a-b)n= Cnan-Cnan-1b+ … +(-1)rCnan-rbr
+ … +(-1)nCnbn
0
1
r
n
对定理的再认识
2、令a=1,b=x
尝试二项式定理的应用:
例1:
尝试二项式定理的应用:
思考:
尝试二项式定理的应用:
练习:
解:(1)
例2. 用二项式定理展开下列各式:
例3、求(x+a)12的展开式中的倒数第4项
解:
二项式定理的应用:
课堂练习
2.求 的展开式的第4项的二项式系数,并求第4项的系数.
解:展开式的第4项的二项式系数
第4项的系数
今天是星期一,那么 天后
的这一天是星期几?
余数是1,所以这一天是星期二
问题探究:
①项数:共n+1项,是关于a与b的齐次多项式
②指数:a的指数从n逐项递减到0,是降幂排列;
b的指数从0逐项递增到n,是升幂排列。
-
小结:
1)注意二项式定理 中二项展开式的特征
2)区别二项式系数,项的系数
3)掌握用通项公式求二项式系数,项的系数及项
10.4 二项式定理
布置作业:
习题10.4 T2 、T3 、T4(1)(2)
A . 必做题
B. 选做题
在
的展开式中,若常数项存在,则n
的最小值.
课后探究:
高二数学课
二 项 式 定 理
问题:
(1)今天是星期一,那么7天后的这一天是星期几呢
(3)如果是 天后的这一天呢?
(2)如果是15天后的这一天呢?
(星期二)
(星期一)
回顾:
尝试二项式定理的发现:
尝试二项式定理的发现:
尝试二项式定理的发现:
发现规律:
对于(a+b)n=
的展开式中an-rbr的系数是在n个括号中,恰有r个括号中取b(其余括号中取a)的组合数 .那么,我们能不能写出(a+b)n的展开式?
将(a+b)n展开的结果又是怎样呢?
归纳提高
引出定理,总结特征
这个公式表示的定理叫做二项式定理,公式
右边的多项式叫做 (a+b) n的 ,
其中 (r=0,1,2,……,n)叫做 ,
叫做二项展开式的通项,用 Tr+1
表示,该项是指展开式的第 项,展开式共有_____个项.
展开式
二项式系数
r+1
n+1
二项式定理
2.系数规律:
2.指数规律:
(1)各项的次数均为n;即为n次齐次式
(2)a的次数由n逐次降到0,
b的次数由0逐次升到n.
1.项数规律:
展开式共有n+1个项
二项式定理
特别地:
1、把b用-b代替
(a-b)n= Cnan-Cnan-1b+ … +(-1)rCnan-rbr
+ … +(-1)nCnbn
0
1
r
n
对定理的再认识
2、令a=1,b=x
尝试二项式定理的应用:
例1:
尝试二项式定理的应用:
思考:
尝试二项式定理的应用:
练习:
解:(1)
例2. 用二项式定理展开下列各式:
例3、求(x+a)12的展开式中的倒数第4项
解:
二项式定理的应用:
课堂练习
2.求 的展开式的第4项的二项式系数,并求第4项的系数.
解:展开式的第4项的二项式系数
第4项的系数
今天是星期一,那么 天后
的这一天是星期几?
余数是1,所以这一天是星期二
问题探究:
①项数:共n+1项,是关于a与b的齐次多项式
②指数:a的指数从n逐项递减到0,是降幂排列;
b的指数从0逐项递增到n,是升幂排列。
-
小结:
1)注意二项式定理 中二项展开式的特征
2)区别二项式系数,项的系数
3)掌握用通项公式求二项式系数,项的系数及项
10.4 二项式定理
布置作业:
习题10.4 T2 、T3 、T4(1)(2)
A . 必做题
B. 选做题
在
的展开式中,若常数项存在,则n
的最小值.
课后探究:
