抛物线及其标准方程
图片预览




文档简介
(共35张PPT)
抛物线及其标准方程(一)
安溪蓝溪中学:龚条枝
生活中存在着各种形式的抛物线
抛物线的生活实例
抛球运动
抛物线的生活实例
探照灯的灯面
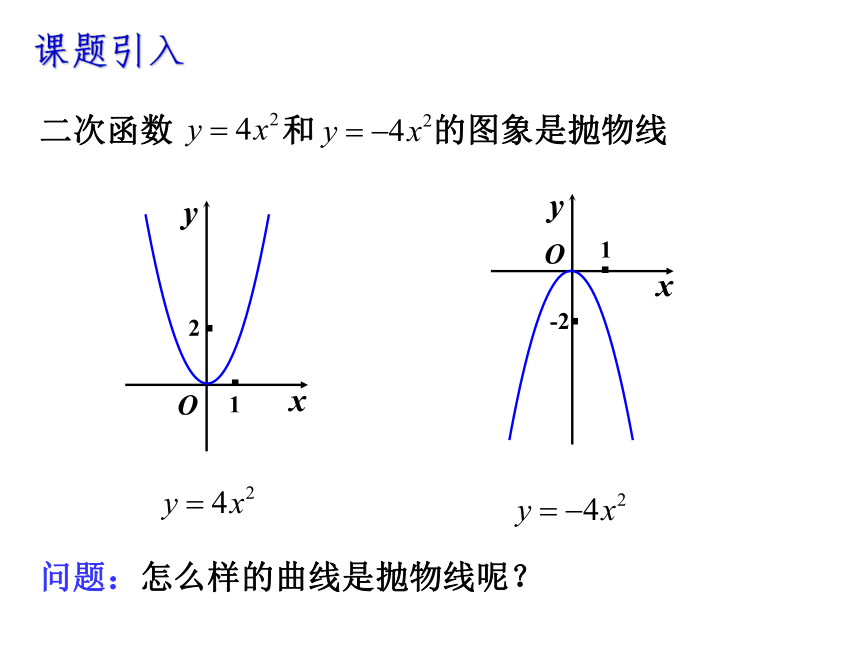
课题引入
问题:怎么样的曲线是抛物线呢?
二次函数 和 的图象是抛物线
.
-2
.
x
y
O
1
.
2
.
x
y
O
1
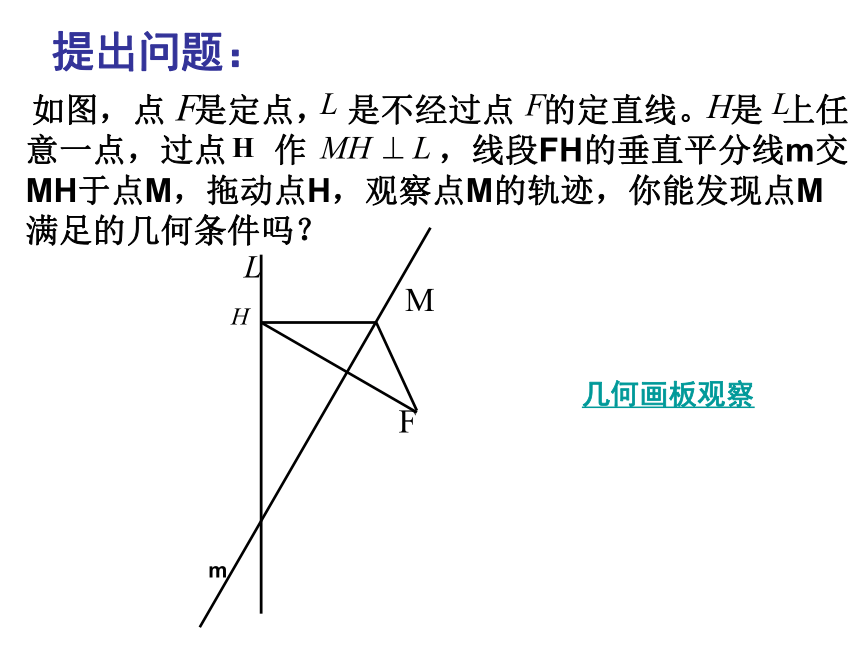
提出问题:
M
F
几何画板观察
如图,点 是定点, 是不经过点 的定直线。 是 上任意一点,过点 作 ,线段FH的垂直平分线m交MH于点M,拖动点H,观察点M的轨迹,你能发现点M满足的几何条件吗?
H
m
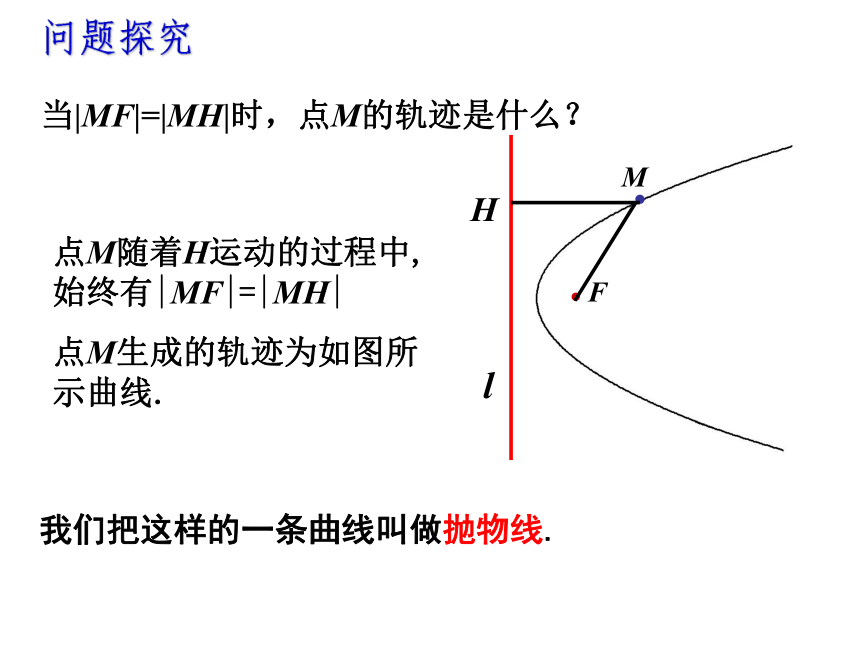
问题探究
点M随着H运动的过程中,始终有|MF|=|MH|
点M生成的轨迹为如图所示曲线.
M
·
F
l
·
我们把这样的一条曲线叫做抛物线.
当|MF|=|MH|时,点M的轨迹是什么?
M
·
F
l
·
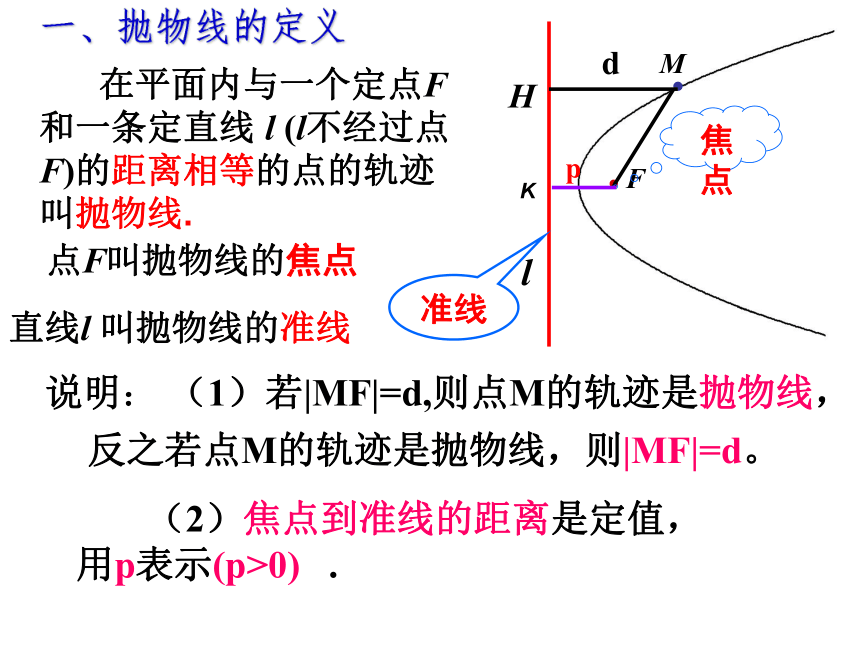
在平面内与一个定点F和一条定直线 l (l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点
准线
焦点
一、抛物线的定义
直线l 叫抛物线的准线
d
说明: (1)若|MF|=d,则点M的轨迹是抛物线,
反之若点M的轨迹是抛物线,则|MF|=d。
(2)焦点到准线的距离是定值,用p表示(p>0) .
p
K
想一想
·
·
F
M
l
d
p
K
H
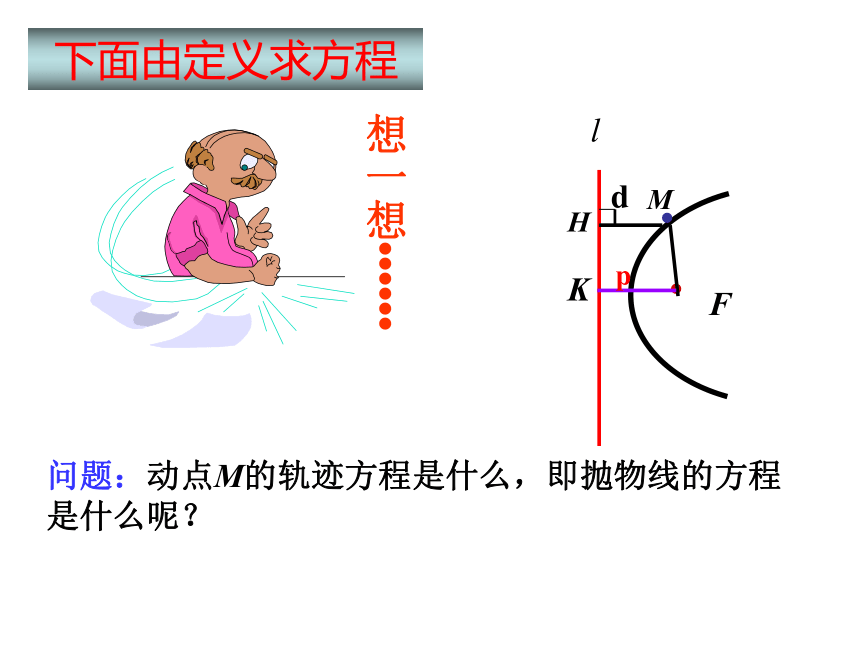
下面由定义求方程
问题:动点M的轨迹方程是什么,即抛物线的方程是什么呢?
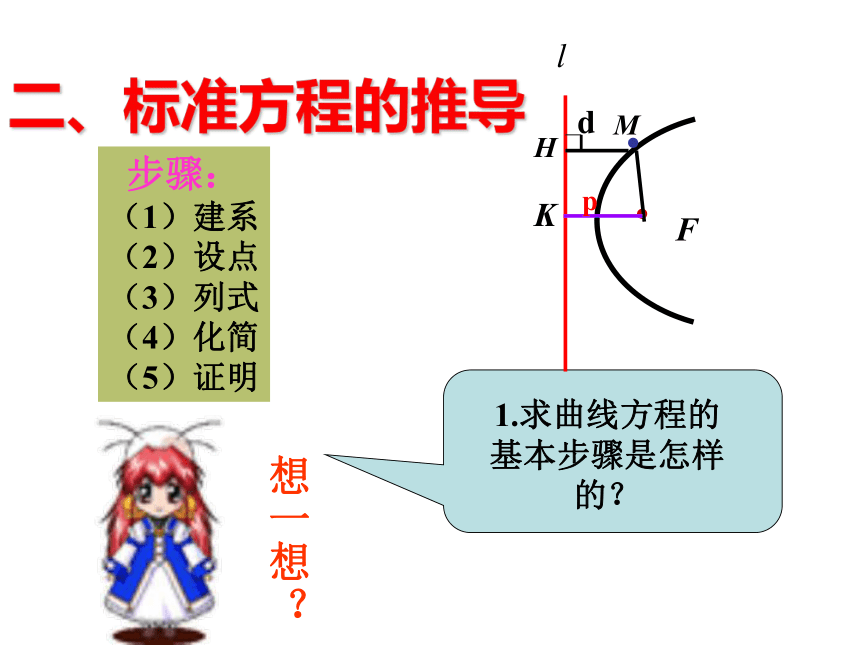
二、标准方程的推导
步骤:(1)建系(2)设点(3)列式(4)化简(5)证明
想一想?
1.求曲线方程的基本步骤是怎样的?
·
·
F
M
l
d
p
K
H
M
·
F
l
·
d
p
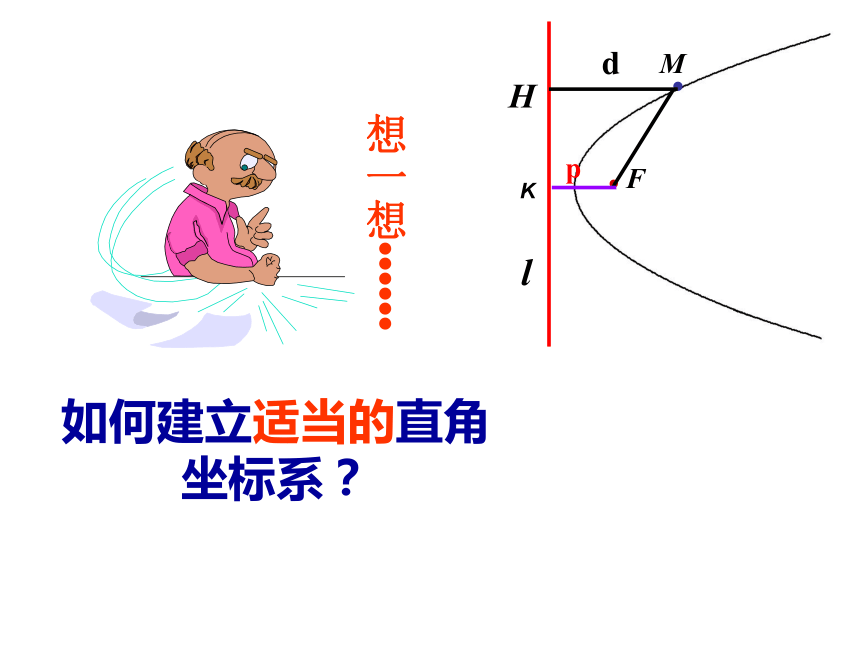
想一想
如何建立适当的直角
坐标系?
K
y
x
o
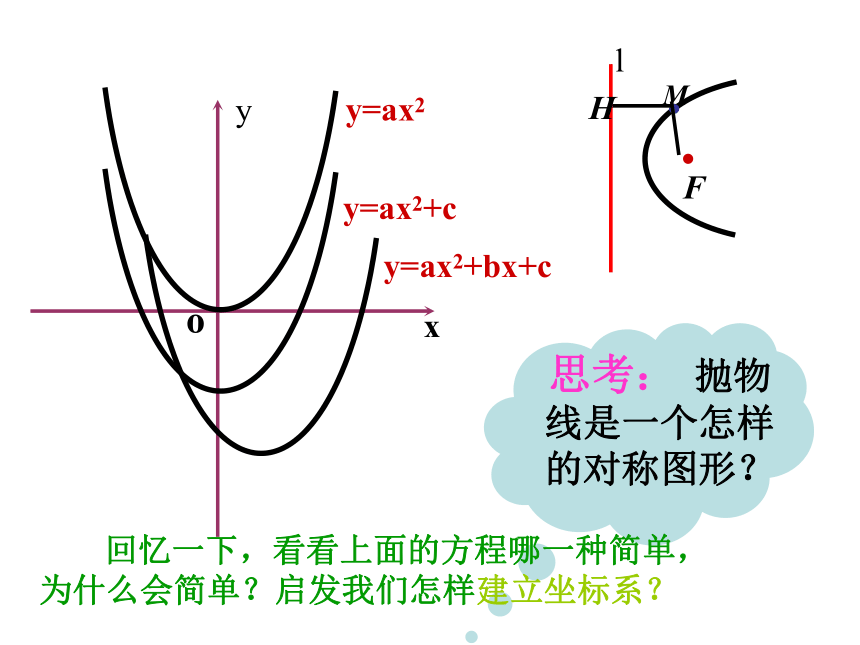
y=ax2+bx+c
y=ax2+c
y=ax2
思考: 抛物线是一个怎样的对称图形?
·
·
F
M
l
H
回忆一下,看看上面的方程哪一种简单,
为什么会简单?启发我们怎样建立坐标系?
作 于点H.
解:以过F且垂直于 l 的直线为x轴,垂足为K.以线段FK的中点O为坐标原点建立直角坐标系xOy.
标准方程的推导
设点 为抛物线上的任意一点 ,
则焦点 ,准线
.
M(x,y)
x
y
O
F
l
K
H
两边平方,整理得
由抛物线的定义得
这就是所求M点的轨迹方程.
因为
所以
.
M(x,y)
x
y
O
F
l
K
H
标准方程的推导
标准方程
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.
.
M(x,y)
x
y
O
F
l
K
H
1、它表示的抛物线焦点在X轴的正半轴上,
焦点F( , 0),准线l:x = -
p
2
p
2
说 明:
2、其中p的几何意义是:
焦点到准线的距离。
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
四种抛物线的对比
四类标准方程及其图形的对应关系
如何判断呢?
想一想:
(1)一次项的变量为抛物线的对称轴,焦点就在对称轴上;
口诀:
(1)一次项的变量如为x(或y),则x轴(或y轴)为抛物线的对称轴,焦点就在x轴(或y轴)上.
(2)一次项系数的正负决定了抛物线的开口方向.
例1、求满足下列条件的抛物线的标准方程:
(1)已知抛物线的焦点坐标是 F(0,-2)
(2)求过点A(-3,2)
x 2 =-8 y
四、 例题讲解
(3)焦点在直线3x-4y-12=0上
(2)求经过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:设抛物线的标准方程为
x2 =2p1y或 y2 = -2p2x ,
把A(-3,2)代入,得
∴抛物线的标准方程为x2 = y或y2 = x 。
抛物线草图
→设标准方程
→求参数P
(1)已知抛物线标准方程是 ,
则它的焦点坐标为 ,准线l 的方程为 。
(2)已知抛物线的焦点坐标是F ,
则它的标准方程是 。
(3)已知抛物线的准线方程是 ,
则它的标准方程是 。
课堂练习:(口答)
y
x
o
﹒
a>0
a<0
(1)已知抛物线的方程为 求它的焦点坐标.
y
x
o
﹒
y
x
o
﹒
你能说出动画演示作抛物线的依据吗
探索内容
例2. 抛物线 上有一点M,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M点的坐标.
应用提高
变式1:已知动点P在抛物线y2 =-4x上,求点P到焦点F与到点M1( -9,5 )的距离之和的最小值.
变式2:已知动点P在抛物线y2 =-4x上, 求点P到其准线与到点M2( -9,7 )的距离之和的最小值.
2、抛物线的四类标准方程与图象之间的对应关系及判断方法
1、抛物线的定义、标准方程及其焦点、准线
六、课堂小结
3、p的几何意义是: 焦点到准线的距离
4、注重数形结合的思想
5、注重分类讨论的思想
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
上下型
七、巩固练习:
1.点M与点F 的距离和它到直线
的距离相等,则点M的轨迹方程是 。
变式:2.点M与点F(4,0)的距离比它到直线 的距离
小1,求点M的轨迹方程。
3.M是抛物线y2 = 2px(P>0)上一点,若点M 的横坐
标为X0,则点M到焦点的距离是——————————.
4. 求顶点在原点,焦点在x轴上的抛物线且截直线2x-y+1=0所得的弦长为 的抛物线的方程.
2011,12、16
变式:2.点M与点F(4,0)的距离比它到直线 的距离
小1,求点M的轨迹方程。
M
F(4,0)
l
x
y
解法二:(直接法)
设M(x,y),
则M点到l的距离为d,
依题意
则
化简为
解法一:
可知原条件 M点到F (4,0)和到 距离相等,
由抛物线的定义,
点M的轨迹是以F (4,0)为焦点, 为准线的抛物线。
,所求方程是
l’
-5
-4
·
·
3.M是抛物线y2 = 2px(P>0)上一点,若点M 的横坐
标为X0,则点M到焦点的距离是——————————.
X0 + —
2
p
O
y
x
.
F
M
.
4、求顶点在原点,焦点在x轴上的抛物线且截直线2x-y+1=0所得的弦长为 的抛物线的方程.
解:设所求的抛物线方程为y2=mx
把y=2x+1代入y2=mx化简得:
4x2+(4-m)x+1=0
所以所求的抛物线方程为y2=12x或y2=-4x.
注意:
7. 在抛物线y2 = 2x上求一点P, 使P到焦点F与到点A ( 3,2 )的距离之和最小.
P
Q
l
A
X
y
O
F
8.抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?
解:抛物线标准方程为:y2= x
1
a
∴2p=
1
a
4a
1
∴焦点坐标是( ,0),准线方程是: x=
4a
1
②当a<0时, , 抛物线的开口向左
p
2
=
1
4a
∴焦点坐标是( ,0),准线方程是: x=
4a
1
1
4a
①当a>0时, , 抛物线的开口向右
p
2
=
1
4a
抛物线及其标准方程(一)
安溪蓝溪中学:龚条枝
生活中存在着各种形式的抛物线
抛物线的生活实例
抛球运动
抛物线的生活实例
探照灯的灯面
课题引入
问题:怎么样的曲线是抛物线呢?
二次函数 和 的图象是抛物线
.
-2
.
x
y
O
1
.
2
.
x
y
O
1
提出问题:
M
F
几何画板观察
如图,点 是定点, 是不经过点 的定直线。 是 上任意一点,过点 作 ,线段FH的垂直平分线m交MH于点M,拖动点H,观察点M的轨迹,你能发现点M满足的几何条件吗?
H
m
问题探究
点M随着H运动的过程中,始终有|MF|=|MH|
点M生成的轨迹为如图所示曲线.
M
·
F
l
·
我们把这样的一条曲线叫做抛物线.
当|MF|=|MH|时,点M的轨迹是什么?
M
·
F
l
·
在平面内与一个定点F和一条定直线 l (l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点
准线
焦点
一、抛物线的定义
直线l 叫抛物线的准线
d
说明: (1)若|MF|=d,则点M的轨迹是抛物线,
反之若点M的轨迹是抛物线,则|MF|=d。
(2)焦点到准线的距离是定值,用p表示(p>0) .
p
K
想一想
·
·
F
M
l
d
p
K
H
下面由定义求方程
问题:动点M的轨迹方程是什么,即抛物线的方程是什么呢?
二、标准方程的推导
步骤:(1)建系(2)设点(3)列式(4)化简(5)证明
想一想?
1.求曲线方程的基本步骤是怎样的?
·
·
F
M
l
d
p
K
H
M
·
F
l
·
d
p
想一想
如何建立适当的直角
坐标系?
K
y
x
o
y=ax2+bx+c
y=ax2+c
y=ax2
思考: 抛物线是一个怎样的对称图形?
·
·
F
M
l
H
回忆一下,看看上面的方程哪一种简单,
为什么会简单?启发我们怎样建立坐标系?
作 于点H.
解:以过F且垂直于 l 的直线为x轴,垂足为K.以线段FK的中点O为坐标原点建立直角坐标系xOy.
标准方程的推导
设点 为抛物线上的任意一点 ,
则焦点 ,准线
.
M(x,y)
x
y
O
F
l
K
H
两边平方,整理得
由抛物线的定义得
这就是所求M点的轨迹方程.
因为
所以
.
M(x,y)
x
y
O
F
l
K
H
标准方程的推导
标准方程
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.
.
M(x,y)
x
y
O
F
l
K
H
1、它表示的抛物线焦点在X轴的正半轴上,
焦点F( , 0),准线l:x = -
p
2
p
2
说 明:
2、其中p的几何意义是:
焦点到准线的距离。
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
四种抛物线的对比
四类标准方程及其图形的对应关系
如何判断呢?
想一想:
(1)一次项的变量为抛物线的对称轴,焦点就在对称轴上;
口诀:
(1)一次项的变量如为x(或y),则x轴(或y轴)为抛物线的对称轴,焦点就在x轴(或y轴)上.
(2)一次项系数的正负决定了抛物线的开口方向.
例1、求满足下列条件的抛物线的标准方程:
(1)已知抛物线的焦点坐标是 F(0,-2)
(2)求过点A(-3,2)
x 2 =-8 y
四、 例题讲解
(3)焦点在直线3x-4y-12=0上
(2)求经过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:设抛物线的标准方程为
x2 =2p1y或 y2 = -2p2x ,
把A(-3,2)代入,得
∴抛物线的标准方程为x2 = y或y2 = x 。
抛物线草图
→设标准方程
→求参数P
(1)已知抛物线标准方程是 ,
则它的焦点坐标为 ,准线l 的方程为 。
(2)已知抛物线的焦点坐标是F ,
则它的标准方程是 。
(3)已知抛物线的准线方程是 ,
则它的标准方程是 。
课堂练习:(口答)
y
x
o
﹒
a>0
a<0
(1)已知抛物线的方程为 求它的焦点坐标.
y
x
o
﹒
y
x
o
﹒
你能说出动画演示作抛物线的依据吗
探索内容
例2. 抛物线 上有一点M,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M点的坐标.
应用提高
变式1:已知动点P在抛物线y2 =-4x上,求点P到焦点F与到点M1( -9,5 )的距离之和的最小值.
变式2:已知动点P在抛物线y2 =-4x上, 求点P到其准线与到点M2( -9,7 )的距离之和的最小值.
2、抛物线的四类标准方程与图象之间的对应关系及判断方法
1、抛物线的定义、标准方程及其焦点、准线
六、课堂小结
3、p的几何意义是: 焦点到准线的距离
4、注重数形结合的思想
5、注重分类讨论的思想
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
上下型
七、巩固练习:
1.点M与点F 的距离和它到直线
的距离相等,则点M的轨迹方程是 。
变式:2.点M与点F(4,0)的距离比它到直线 的距离
小1,求点M的轨迹方程。
3.M是抛物线y2 = 2px(P>0)上一点,若点M 的横坐
标为X0,则点M到焦点的距离是——————————.
4. 求顶点在原点,焦点在x轴上的抛物线且截直线2x-y+1=0所得的弦长为 的抛物线的方程.
2011,12、16
变式:2.点M与点F(4,0)的距离比它到直线 的距离
小1,求点M的轨迹方程。
M
F(4,0)
l
x
y
解法二:(直接法)
设M(x,y),
则M点到l的距离为d,
依题意
则
化简为
解法一:
可知原条件 M点到F (4,0)和到 距离相等,
由抛物线的定义,
点M的轨迹是以F (4,0)为焦点, 为准线的抛物线。
,所求方程是
l’
-5
-4
·
·
3.M是抛物线y2 = 2px(P>0)上一点,若点M 的横坐
标为X0,则点M到焦点的距离是——————————.
X0 + —
2
p
O
y
x
.
F
M
.
4、求顶点在原点,焦点在x轴上的抛物线且截直线2x-y+1=0所得的弦长为 的抛物线的方程.
解:设所求的抛物线方程为y2=mx
把y=2x+1代入y2=mx化简得:
4x2+(4-m)x+1=0
所以所求的抛物线方程为y2=12x或y2=-4x.
注意:
7. 在抛物线y2 = 2x上求一点P, 使P到焦点F与到点A ( 3,2 )的距离之和最小.
P
Q
l
A
X
y
O
F
8.抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?
解:抛物线标准方程为:y2= x
1
a
∴2p=
1
a
4a
1
∴焦点坐标是( ,0),准线方程是: x=
4a
1
②当a<0时, , 抛物线的开口向左
p
2
=
1
4a
∴焦点坐标是( ,0),准线方程是: x=
4a
1
1
4a
①当a>0时, , 抛物线的开口向右
p
2
=
1
4a
