定积分的简单应用
图片预览



文档简介
定积分的简单应用
教材分析
“定积分的简单应用”是人教A版《普通高中课程标准实验教科书数学》选修2-2第一章1.7的内容。从题目中可以看出,这一节教学的要求就是让学生在充分认识导数与积分的概念,计算,几何意义的基础上,掌握用积分手段解决实际问题的基本思想和方法,在学习过程中了解导数与积分的工具性作用,从而进一步认识到数学知识的实用价值以及数学在实际应用中的强大生命力。在整个高中数学体系中,这部分内容也是学生在高等学校进一步学习数学的基础。
教学目标(以教材为背景,根据课标要求,设计了本节课的教学目标)
知识与技能目标:
(1)应用定积分解决平面图形的面积、变速直线运动的路程问题;
(2)学会将实际问题化归为定积分的问题。
过程与方法目标:
通过体验解决问题的过程,体现定积分的使用价值,加强观察能力和归纳能力,强化数形结合和化归思想的思维意识,达到将数学和其他学科进行转化融合的目的。
情感态度与价值观目标:
通过教学过程中的观察、思考、总结,养成自主学习的良好学习习惯,培养数学知识运用于生活的意识。
三、 教学重点与难点
1、重点:应用定积分解决平面图形的面积和变速直线运动的路程问题,在解决问题的过程中体验定积分的价值。
2、难点:将实际问题化归为定积分的问题。
四、教学用具:多媒体
五、教学设计
教学环节 教学设计 师生互动 设计意图
一、创设情境引出新课 1、生活实例:实例1:国家大剧院的主题构造类似半球的构造,如何计算建造时中间玻璃段的使用面积?边缘的玻璃形状属于曲边梯形,要计算使用面积可以通过计算曲边梯形的面积实现。实例2:一辆做变速直线运动的汽车,我们如何计算它行驶的路程?2、复习回顾:如何计算曲边梯形的面积? 3、引入课题:定积分的简单应用 学生:观察。教师:启发,引导学生:思考,回忆。学生:疑惑,思考,感受。教师:启发,引导。学生:复习,回忆老师:引入课题 数学源于生活,又服务于生活。通过对国家大剧院的观察,创设问题情境,体验数学在现实生活中的无处不在,激发学生的学习热情,引导他们积极主动的参与到学习中来。启发学生把物理问题与数学知识联系起来,训练学生对学科间的思维转换和综合思维能力。学生感受定积分的工具性作用与应用价值。在生活实例的启发下,引导学生把所学知识与实际问题联系起来,回忆如何计算曲边梯形面积。这是这节课的知识基础。引入本节课的课题。
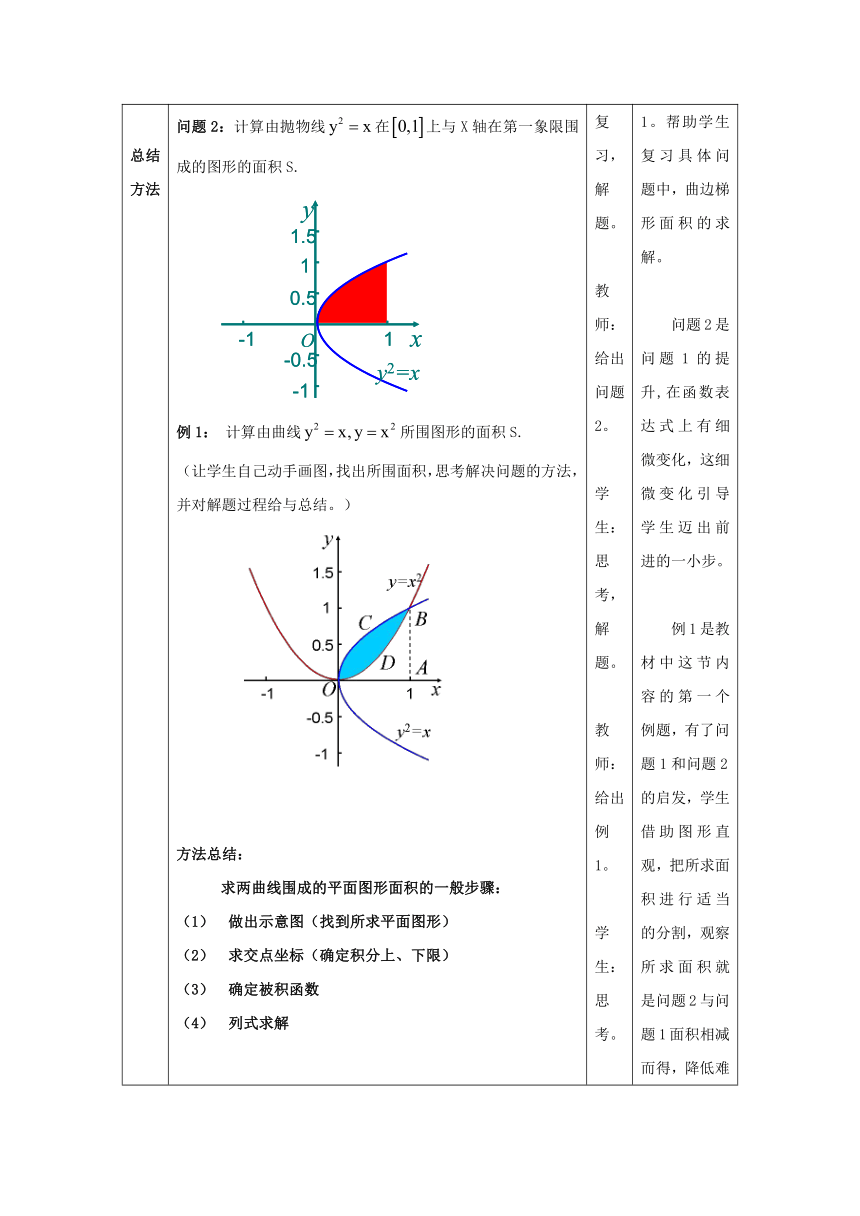
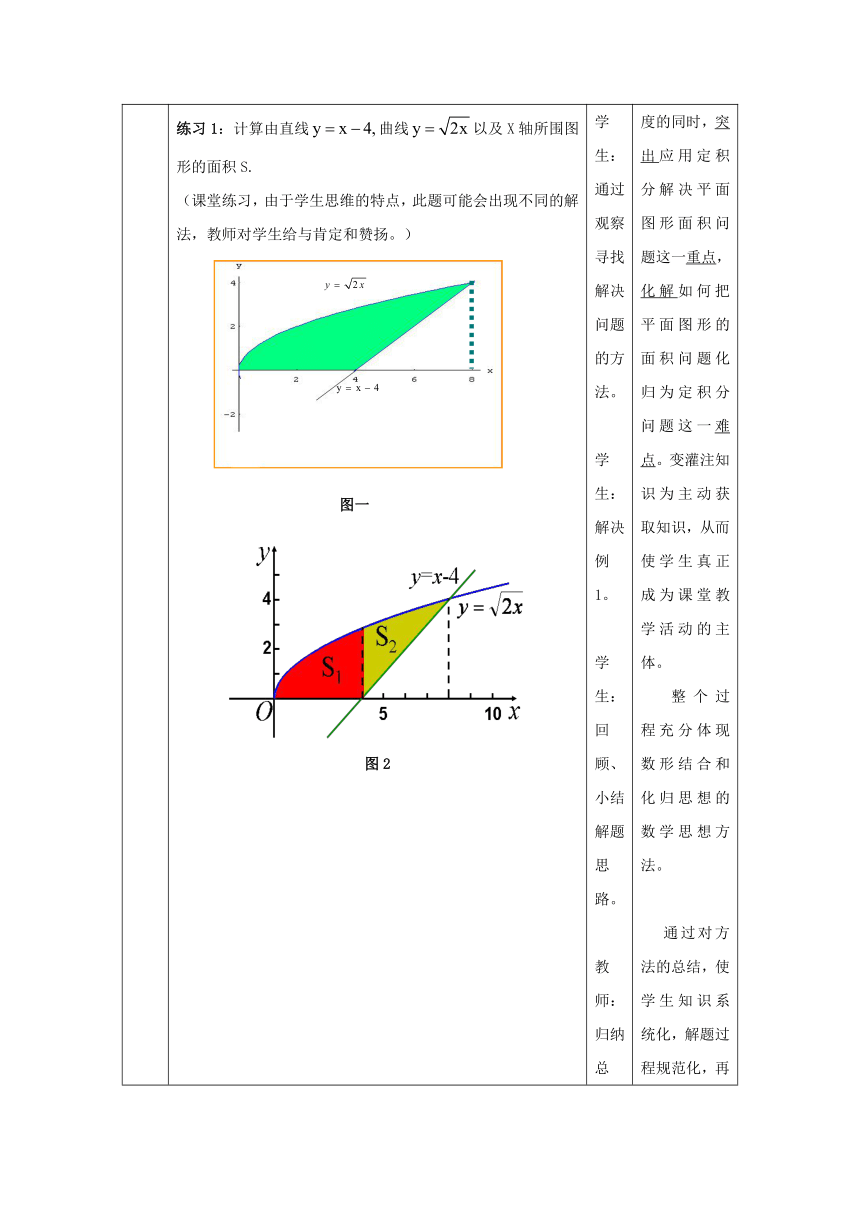
二、例题讲解总结方法 例1: 计算由曲线所围图形的面积S.(降低难度,有利学生理解)问题1:计算由抛物线在上与X轴在第一象限围成图形的面积S.问题2:计算由抛物线在上与X轴在第一象限围成的图形的面积S.例1: 计算由曲线所围图形的面积S.(让学生自己动手画图,找出所围面积,思考解决问题的方法,并对解题过程给与总结。)方法总结:求两曲线围成的平面图形面积的一般步骤:做出示意图(找到所求平面图形)求交点坐标(确定积分上、下限)确定被积函数列式求解练习1:计算由直线曲线以及X轴所围图形的面积S.(课堂练习,由于学生思维的特点,此题可能会出现不同的解法,教师对学生给与肯定和赞扬。) 图一图2 教师:给出问题1。学生:复习,解题。教师:给出问题2。学生:思考,解题。教师:给出例1。学生:思考。学生:通过观察寻找解决问题的方法。学生:解决例1。学生:回顾、小结解题思路。教师:归纳总结。学生:运用所学知识解决问题。老师:展示不同解法,分析,讲解。学生:交流,讨论,体会。 例题讲解,掌握方法。为了有利学生的理解掌握,首先降低难度。把例1分三步进行。第一步,先提出问题1。帮助学生复习具体问题中,曲边梯形面积的求解。问题2是问题1的提升,在函数表达式上有细微变化,这细微变化引导学生迈出前进的一小步。例1是教材中这节内容的第一个例题,有了问题1和问题2的启发,学生借助图形直观,把所求面积进行适当的分割,观察所求面积就是问题2与问题1面积相减而得,降低难度的同时,突出应用定积分解决平面图形面积问题这一重点,化解如何把平面图形的面积问题化归为定积分问题这一难点。变灌注知识为主动获取知识,从而使学生真正成为课堂教学活动的主体。整个过程充分体现数形结合和化归思想的数学思想方法。通过对方法的总结,使学生知识系统化,解题过程规范化,再一次突出重难点,加强学生对这一方法使用的意识。循序渐进,巩固知识。这是一道随堂练习题,是例1的深入和扩展,学生在课堂上给予思考,解决。考虑到学生思维各有特点,所以对问题解决的方法可能会有所不同。有可能直接面积相减而得,也有可能把所求面积分两部分相加而得。教师对学生主要出现的不同解法进行投影分析,并进行比较,学生体会这两种方法的区别及联系,加强对重难点的化解。学生运用新知识解决问题,可以获得极大的成就感,既提高了学习兴趣,又加强学生使用数学知识的意识。突出应用这一主题。
三、学科综合延伸扩展 1、变速直线运动的路程问题:作变速直线运动的物体所经过的路程S,等于其速度函数V=V(t)(V(t)≥0),在时间区间上的定积分. 例2:一辆汽车的速度曲线如图所示,求汽车在这1min行驶的路程。(在物理实际问题中的应用,通过对知识的复习和之前的学习,学生可以自己思考解决问题的方法)练习2:一物体沿直线以v=2t+3(t的单位:s,v的单位:m/s)的速度运动,求该物体在3~5s间行进的路程(学生随堂练习,强化知识) 学生:思考,回忆,说出看法。教师:总结,给出式子。教师:给出例2。学生:思考解决问题的方法。教师:引导学生解决问题。教师:给出练习。 加强学科整合,体现数学知识魅力这节课的核心是对定积分的使用,这种使用不仅可以体现在求平面图形的面积,还可以运用于其他学科。所以,引入物理学中变速直线运动的路程问题,即加强学生对之前所学知识的进一步应用,又能让学生掌握如何将实际问题化归为定积分的问题并加以解决,化解本节课的难点,让他们体验到数学的魅力所在。灵活运用,通过相应的练习,强化对难点的化解,学会运用所学知识解决实际问题,将数学知识运用到生活中来。
四、课堂小结自我评价 1、小结:(1)定积分在几何中的应用(2)定积分在物理中的应用2、求两曲线围成的平面图形面积的步骤?3、定积分在物理应用中的问题。 学生:回顾与思考,并解答。老师:总结。 学生对本节内容回顾与小结,使知识系统化,培养学生的逻辑思维能力,找出自己不清楚的知识点,通过及时的反馈信息为下节课的教学做好准备。
五、布置作业 作业:58页练习 课后作业自主完成 作业是为了巩固知识,应与这节课所学内容紧密相连。
六、板书设计 定积分的简单应用定积分在几何中的应用解题步骤3、变速直线运动的路程问题 清楚明了,简洁有序的板书,有利于知识的回顾与总结。
六、教法与学法
教法:本节课充分体现了“教师为主导,学生为主体”的教学原则,展现获取知识和方法的思维过程。主要体现在以下几个方面
(1)新课引入时,从简单、生动的实例出发,激发学生学习热情,学生以轻松的心态投入学习,突出数学在实际生活中的应用。
(2)例题讲解时,以学生为中心,教师引导,对不同的解法给与肯定和赞扬,用老师鼓励的语言感染学生,学生抱着愉悦的心情投入到数学的学习中来,学习新知识的同时掌握解决问题的方法。
(3)物理应用时,加入数学与其他学科的整合,凸显数学的实用价值,加强学科间的紧密关联。
学法:强化数形结合和化归思想的数学思想方法,形成在生活中使用数学的意识,这种使用不仅仅局限于单纯的数学问题,还可以运用到生活的各个方面。
七、教学评价
教师评价:根据定积分的定义,定积分既有几何背景,又有物理背景,也就是说,定积分与这些知识有着天然的联系。譬如:求几何图形的面积,求路程、电压、功等。而这些实际上也是与现实生活紧密相关的问题,这些问题的解决,从侧面展现了数学思想方法应用的广泛性,学生深切体会到:数学来源于生活,同时服务于生活。
教学过程评价:新课标要求:学习的全过程需要学生的参与,学生是学习的主体和中心。围绕这个宗旨,我在课堂内容编排的思路如下:首先,联系现实生活上,由易到难,结合最基本的、学生所熟知的生活实例和前课知识,由浅入深地对学生加以引导,使他们能够充分思考,发挥学习的主观能动性,自主参与到学习中去。
学生评价:通过课堂反应、练习,课后作业等给予反馈、评价。
哎呀,里程表坏了,你能帮我算算我走了多少路程吗
A
O
10 20 30 40 50 60
40
30
20
10
t/s
v/m/s
电脑投影
例题
教材分析
“定积分的简单应用”是人教A版《普通高中课程标准实验教科书数学》选修2-2第一章1.7的内容。从题目中可以看出,这一节教学的要求就是让学生在充分认识导数与积分的概念,计算,几何意义的基础上,掌握用积分手段解决实际问题的基本思想和方法,在学习过程中了解导数与积分的工具性作用,从而进一步认识到数学知识的实用价值以及数学在实际应用中的强大生命力。在整个高中数学体系中,这部分内容也是学生在高等学校进一步学习数学的基础。
教学目标(以教材为背景,根据课标要求,设计了本节课的教学目标)
知识与技能目标:
(1)应用定积分解决平面图形的面积、变速直线运动的路程问题;
(2)学会将实际问题化归为定积分的问题。
过程与方法目标:
通过体验解决问题的过程,体现定积分的使用价值,加强观察能力和归纳能力,强化数形结合和化归思想的思维意识,达到将数学和其他学科进行转化融合的目的。
情感态度与价值观目标:
通过教学过程中的观察、思考、总结,养成自主学习的良好学习习惯,培养数学知识运用于生活的意识。
三、 教学重点与难点
1、重点:应用定积分解决平面图形的面积和变速直线运动的路程问题,在解决问题的过程中体验定积分的价值。
2、难点:将实际问题化归为定积分的问题。
四、教学用具:多媒体
五、教学设计
教学环节 教学设计 师生互动 设计意图
一、创设情境引出新课 1、生活实例:实例1:国家大剧院的主题构造类似半球的构造,如何计算建造时中间玻璃段的使用面积?边缘的玻璃形状属于曲边梯形,要计算使用面积可以通过计算曲边梯形的面积实现。实例2:一辆做变速直线运动的汽车,我们如何计算它行驶的路程?2、复习回顾:如何计算曲边梯形的面积? 3、引入课题:定积分的简单应用 学生:观察。教师:启发,引导学生:思考,回忆。学生:疑惑,思考,感受。教师:启发,引导。学生:复习,回忆老师:引入课题 数学源于生活,又服务于生活。通过对国家大剧院的观察,创设问题情境,体验数学在现实生活中的无处不在,激发学生的学习热情,引导他们积极主动的参与到学习中来。启发学生把物理问题与数学知识联系起来,训练学生对学科间的思维转换和综合思维能力。学生感受定积分的工具性作用与应用价值。在生活实例的启发下,引导学生把所学知识与实际问题联系起来,回忆如何计算曲边梯形面积。这是这节课的知识基础。引入本节课的课题。
二、例题讲解总结方法 例1: 计算由曲线所围图形的面积S.(降低难度,有利学生理解)问题1:计算由抛物线在上与X轴在第一象限围成图形的面积S.问题2:计算由抛物线在上与X轴在第一象限围成的图形的面积S.例1: 计算由曲线所围图形的面积S.(让学生自己动手画图,找出所围面积,思考解决问题的方法,并对解题过程给与总结。)方法总结:求两曲线围成的平面图形面积的一般步骤:做出示意图(找到所求平面图形)求交点坐标(确定积分上、下限)确定被积函数列式求解练习1:计算由直线曲线以及X轴所围图形的面积S.(课堂练习,由于学生思维的特点,此题可能会出现不同的解法,教师对学生给与肯定和赞扬。) 图一图2 教师:给出问题1。学生:复习,解题。教师:给出问题2。学生:思考,解题。教师:给出例1。学生:思考。学生:通过观察寻找解决问题的方法。学生:解决例1。学生:回顾、小结解题思路。教师:归纳总结。学生:运用所学知识解决问题。老师:展示不同解法,分析,讲解。学生:交流,讨论,体会。 例题讲解,掌握方法。为了有利学生的理解掌握,首先降低难度。把例1分三步进行。第一步,先提出问题1。帮助学生复习具体问题中,曲边梯形面积的求解。问题2是问题1的提升,在函数表达式上有细微变化,这细微变化引导学生迈出前进的一小步。例1是教材中这节内容的第一个例题,有了问题1和问题2的启发,学生借助图形直观,把所求面积进行适当的分割,观察所求面积就是问题2与问题1面积相减而得,降低难度的同时,突出应用定积分解决平面图形面积问题这一重点,化解如何把平面图形的面积问题化归为定积分问题这一难点。变灌注知识为主动获取知识,从而使学生真正成为课堂教学活动的主体。整个过程充分体现数形结合和化归思想的数学思想方法。通过对方法的总结,使学生知识系统化,解题过程规范化,再一次突出重难点,加强学生对这一方法使用的意识。循序渐进,巩固知识。这是一道随堂练习题,是例1的深入和扩展,学生在课堂上给予思考,解决。考虑到学生思维各有特点,所以对问题解决的方法可能会有所不同。有可能直接面积相减而得,也有可能把所求面积分两部分相加而得。教师对学生主要出现的不同解法进行投影分析,并进行比较,学生体会这两种方法的区别及联系,加强对重难点的化解。学生运用新知识解决问题,可以获得极大的成就感,既提高了学习兴趣,又加强学生使用数学知识的意识。突出应用这一主题。
三、学科综合延伸扩展 1、变速直线运动的路程问题:作变速直线运动的物体所经过的路程S,等于其速度函数V=V(t)(V(t)≥0),在时间区间上的定积分. 例2:一辆汽车的速度曲线如图所示,求汽车在这1min行驶的路程。(在物理实际问题中的应用,通过对知识的复习和之前的学习,学生可以自己思考解决问题的方法)练习2:一物体沿直线以v=2t+3(t的单位:s,v的单位:m/s)的速度运动,求该物体在3~5s间行进的路程(学生随堂练习,强化知识) 学生:思考,回忆,说出看法。教师:总结,给出式子。教师:给出例2。学生:思考解决问题的方法。教师:引导学生解决问题。教师:给出练习。 加强学科整合,体现数学知识魅力这节课的核心是对定积分的使用,这种使用不仅可以体现在求平面图形的面积,还可以运用于其他学科。所以,引入物理学中变速直线运动的路程问题,即加强学生对之前所学知识的进一步应用,又能让学生掌握如何将实际问题化归为定积分的问题并加以解决,化解本节课的难点,让他们体验到数学的魅力所在。灵活运用,通过相应的练习,强化对难点的化解,学会运用所学知识解决实际问题,将数学知识运用到生活中来。
四、课堂小结自我评价 1、小结:(1)定积分在几何中的应用(2)定积分在物理中的应用2、求两曲线围成的平面图形面积的步骤?3、定积分在物理应用中的问题。 学生:回顾与思考,并解答。老师:总结。 学生对本节内容回顾与小结,使知识系统化,培养学生的逻辑思维能力,找出自己不清楚的知识点,通过及时的反馈信息为下节课的教学做好准备。
五、布置作业 作业:58页练习 课后作业自主完成 作业是为了巩固知识,应与这节课所学内容紧密相连。
六、板书设计 定积分的简单应用定积分在几何中的应用解题步骤3、变速直线运动的路程问题 清楚明了,简洁有序的板书,有利于知识的回顾与总结。
六、教法与学法
教法:本节课充分体现了“教师为主导,学生为主体”的教学原则,展现获取知识和方法的思维过程。主要体现在以下几个方面
(1)新课引入时,从简单、生动的实例出发,激发学生学习热情,学生以轻松的心态投入学习,突出数学在实际生活中的应用。
(2)例题讲解时,以学生为中心,教师引导,对不同的解法给与肯定和赞扬,用老师鼓励的语言感染学生,学生抱着愉悦的心情投入到数学的学习中来,学习新知识的同时掌握解决问题的方法。
(3)物理应用时,加入数学与其他学科的整合,凸显数学的实用价值,加强学科间的紧密关联。
学法:强化数形结合和化归思想的数学思想方法,形成在生活中使用数学的意识,这种使用不仅仅局限于单纯的数学问题,还可以运用到生活的各个方面。
七、教学评价
教师评价:根据定积分的定义,定积分既有几何背景,又有物理背景,也就是说,定积分与这些知识有着天然的联系。譬如:求几何图形的面积,求路程、电压、功等。而这些实际上也是与现实生活紧密相关的问题,这些问题的解决,从侧面展现了数学思想方法应用的广泛性,学生深切体会到:数学来源于生活,同时服务于生活。
教学过程评价:新课标要求:学习的全过程需要学生的参与,学生是学习的主体和中心。围绕这个宗旨,我在课堂内容编排的思路如下:首先,联系现实生活上,由易到难,结合最基本的、学生所熟知的生活实例和前课知识,由浅入深地对学生加以引导,使他们能够充分思考,发挥学习的主观能动性,自主参与到学习中去。
学生评价:通过课堂反应、练习,课后作业等给予反馈、评价。
哎呀,里程表坏了,你能帮我算算我走了多少路程吗
A
O
10 20 30 40 50 60
40
30
20
10
t/s
v/m/s
电脑投影
例题
