七年级数学多边形的内角和
文档属性
| 名称 | 七年级数学多边形的内角和 |  | |
| 格式 | zip | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-02 14:35:45 | ||
图片预览


文档简介
(共33张PPT)
多边形的内角和
多边形的内角和
七年级人教版下册 第七章 三角形
花园街
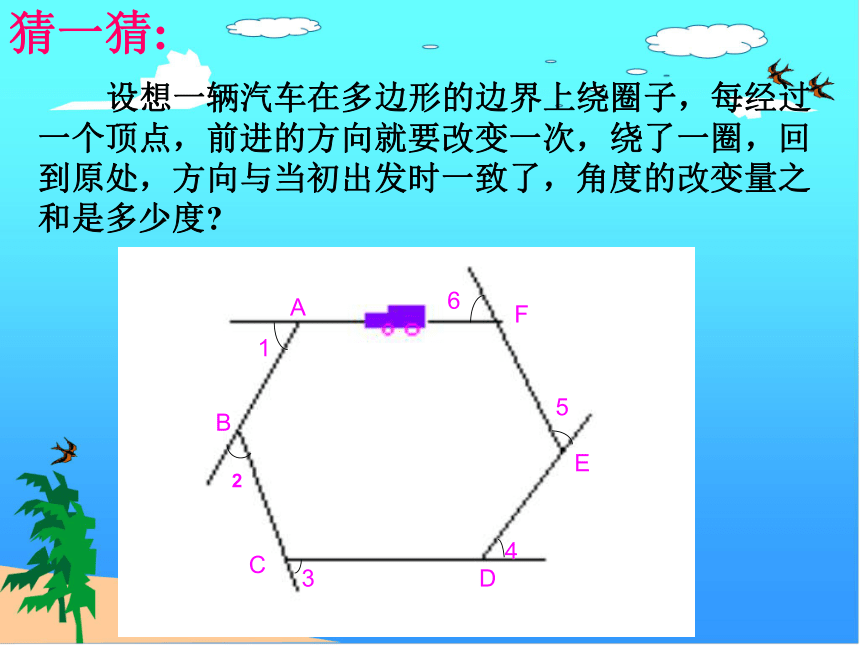
设想一辆汽车在多边形的边界上绕圈子,每经过一个顶点,前进的方向就要改变一次,绕了一圈,回到原处,方向与当初出发时一致了,角度的改变量之和是多少度
猜一猜:
2
1
3
4
5
6
A
B
C
D
E
F
三角形内角和等于180°
长方形、正方形的内角和等于360°
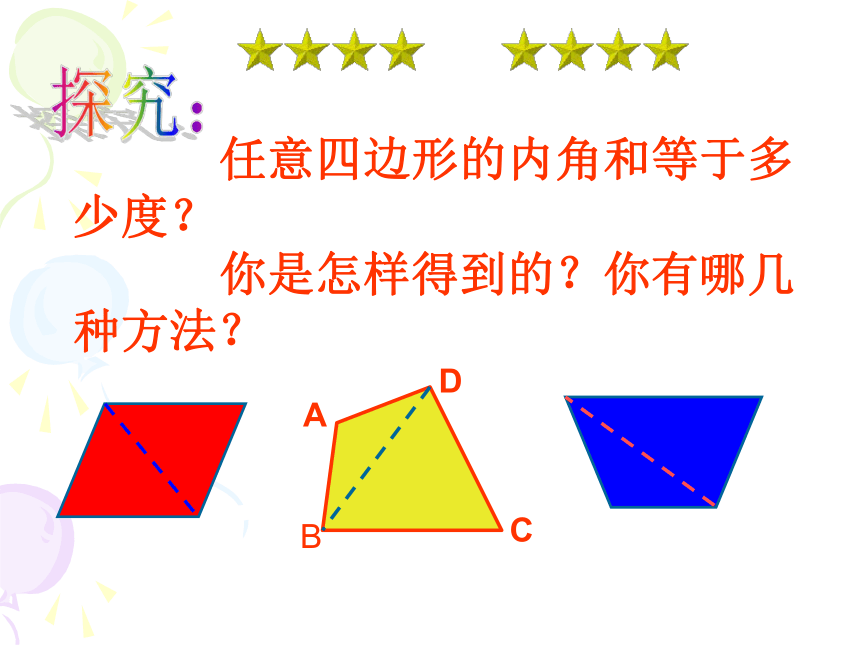
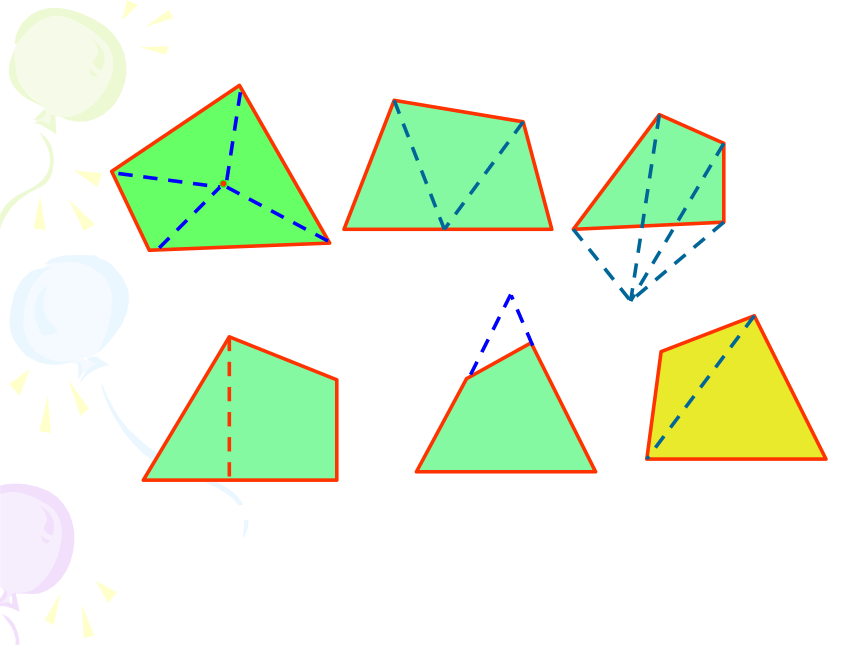
任意四边形的内角和等于多少度?
你是怎样得到的?你有哪几种方法?
A
B
C
D
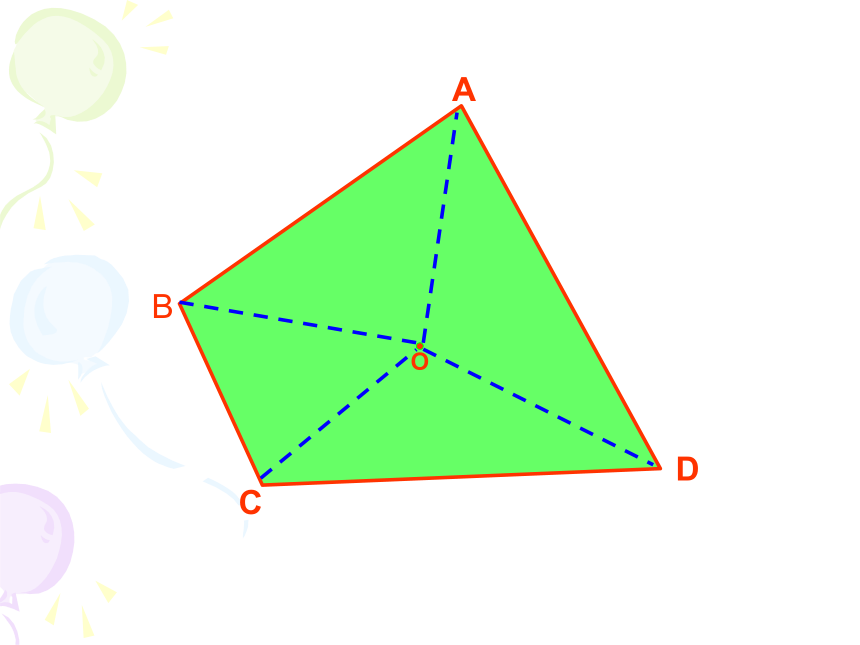
A
B
C
D
O
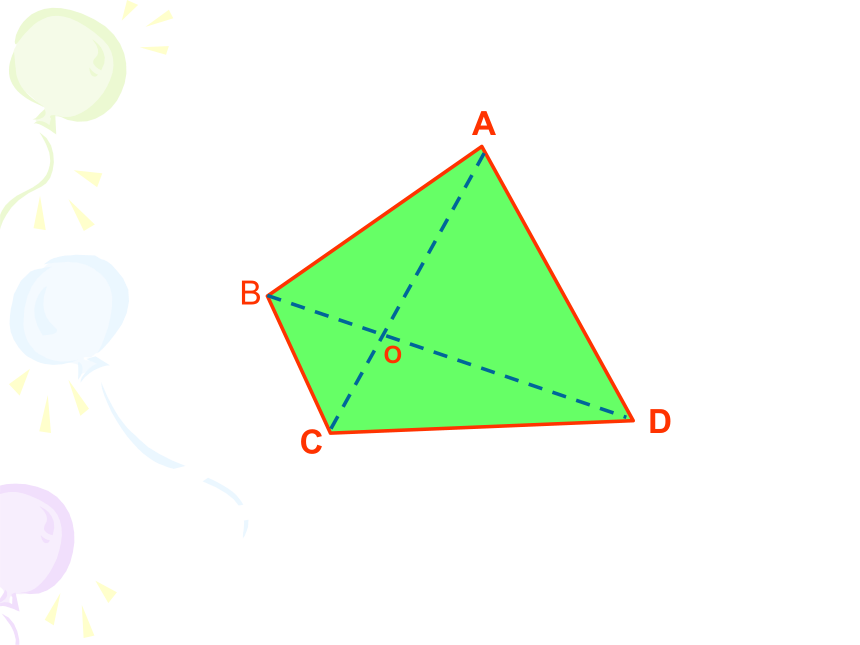
A
B
C
D
O
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
任选一种你喜欢的方法,求五边形的内角和。
D
E
C
A
B
2
1
4
内角和
三角形个数
从一个顶点引出对角线数
边数
5
6
2
3
3×180°=540 °
.
.
.
.
.
.
.
.
.
.
3
4
4×180°=720°
(n-2)×180°
n
n-3
n-2
7
5×180°=900°
4
5
n边形的内角和是多少度?
2×180°=360 °
五边形
六边形
根据以上的探讨,就得出了多边形的内角和公式:
n边形的内角和等于
(n-2)·180°
例1.如果一个四边形的一组对角互补, 那么另一组对角有什么关系?
D
A
B
C
解: 如右图,四边形ABCD中,
∠A+∠C=180°.
∵ ∠A+∠B+∠C+∠D
=(4-2) ×180°=360 °
∴ ∠B+∠D=360°-(∠A+∠C)
=360°-180°=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补.
5个金蛋你可以任选一个,如果出现“恭喜你”的字样,你将直接过关;否则将有考验你的数学问题,当然你可以自己作答,也可以求助你的同学.
七(5)班同学们, 大家好!
快乐之旅
1
2
3
4
5
1
1、十二边形的内角和等于 。
1800°
C
2
2、一个多边形的内角和等于720度,那么这个多边形是 边形.
六
恭喜你,过关了!
3
4
4、多边形的内角和随着边数的增加而 ,边数增加一条时它的内角和增加 。
增加
180°
5
x°
120°
150°
2x°
5.求下列图形中x的值
如果将刚才的六边形换为n边形可以得到同样的结果吗?
(1)各内角与相邻外角互补;
(2)外角和=n个平角-内角和
=n×180°-(n-2) × 180°
=360°
结论:n边形的外角和等于360°
设想一辆汽车在多边形的边界上绕圈子,每经过一个顶点,前进的方向就要改变一次,绕了一圈,回到原处,方向与当初出发时一致了,角度的改变量之和是多少度
猜一猜:
2
1
3
4
5
6
A
B
C
D
E
F
1
2
3
4
A
B
C
D
E
F
5
6
提示:考虑以下问题:
(1)各内角与相邻外角有什么关系?
(2)六边形的6个外角加上与它
们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和、
外角和有什么关系?
六边形的外角和=6个平角-六边 形的内角和
=6×180°-(6-2) × 180°
=360°
一、判断:
(1)多边形边数增加时,它的外角和也随着增加( )
(2)正六边形的每个外角都等于60度( )
(3)所有正多边形的外角和都相等( )
×
二、填空:
1.已知多边形的每个内角都是120度,则这个多边形是_______.
2.如果某个多边形的内角和等于它的外角和,那么这个多边形的边数是________.
六边形
四边形
通过这节课的学习活动你有哪些收获?
你还有什么困惑吗?
多边形的内角和
多边形的内角和
七年级人教版下册 第七章 三角形
花园街
设想一辆汽车在多边形的边界上绕圈子,每经过一个顶点,前进的方向就要改变一次,绕了一圈,回到原处,方向与当初出发时一致了,角度的改变量之和是多少度
猜一猜:
2
1
3
4
5
6
A
B
C
D
E
F
三角形内角和等于180°
长方形、正方形的内角和等于360°
任意四边形的内角和等于多少度?
你是怎样得到的?你有哪几种方法?
A
B
C
D
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
任选一种你喜欢的方法,求五边形的内角和。
D
E
C
A
B
2
1
4
内角和
三角形个数
从一个顶点引出对角线数
边数
5
6
2
3
3×180°=540 °
.
.
.
.
.
.
.
.
.
.
3
4
4×180°=720°
(n-2)×180°
n
n-3
n-2
7
5×180°=900°
4
5
n边形的内角和是多少度?
2×180°=360 °
五边形
六边形
根据以上的探讨,就得出了多边形的内角和公式:
n边形的内角和等于
(n-2)·180°
例1.如果一个四边形的一组对角互补, 那么另一组对角有什么关系?
D
A
B
C
解: 如右图,四边形ABCD中,
∠A+∠C=180°.
∵ ∠A+∠B+∠C+∠D
=(4-2) ×180°=360 °
∴ ∠B+∠D=360°-(∠A+∠C)
=360°-180°=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补.
5个金蛋你可以任选一个,如果出现“恭喜你”的字样,你将直接过关;否则将有考验你的数学问题,当然你可以自己作答,也可以求助你的同学.
七(5)班同学们, 大家好!
快乐之旅
1
2
3
4
5
1
1、十二边形的内角和等于 。
1800°
C
2
2、一个多边形的内角和等于720度,那么这个多边形是 边形.
六
恭喜你,过关了!
3
4
4、多边形的内角和随着边数的增加而 ,边数增加一条时它的内角和增加 。
增加
180°
5
x°
120°
150°
2x°
5.求下列图形中x的值
如果将刚才的六边形换为n边形可以得到同样的结果吗?
(1)各内角与相邻外角互补;
(2)外角和=n个平角-内角和
=n×180°-(n-2) × 180°
=360°
结论:n边形的外角和等于360°
设想一辆汽车在多边形的边界上绕圈子,每经过一个顶点,前进的方向就要改变一次,绕了一圈,回到原处,方向与当初出发时一致了,角度的改变量之和是多少度
猜一猜:
2
1
3
4
5
6
A
B
C
D
E
F
1
2
3
4
A
B
C
D
E
F
5
6
提示:考虑以下问题:
(1)各内角与相邻外角有什么关系?
(2)六边形的6个外角加上与它
们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和、
外角和有什么关系?
六边形的外角和=6个平角-六边 形的内角和
=6×180°-(6-2) × 180°
=360°
一、判断:
(1)多边形边数增加时,它的外角和也随着增加( )
(2)正六边形的每个外角都等于60度( )
(3)所有正多边形的外角和都相等( )
×
二、填空:
1.已知多边形的每个内角都是120度,则这个多边形是_______.
2.如果某个多边形的内角和等于它的外角和,那么这个多边形的边数是________.
六边形
四边形
通过这节课的学习活动你有哪些收获?
你还有什么困惑吗?
