山东省临清市大辛庄办事处中学2011-2012学年八年级下学期期中考试数学试题
文档属性
| 名称 | 山东省临清市大辛庄办事处中学2011-2012学年八年级下学期期中考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 184.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-02 00:00:00 | ||
图片预览



文档简介
(时间120分钟,满分120分)
选择题(本题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项符合题目要求,请把正确选项的序号填在答卷的相应位置)
1.计算的结果是( )
A.3 B. C. D.9
2.三角形在正方形网格纸中的位置如图所示,
则sinα的值是( )
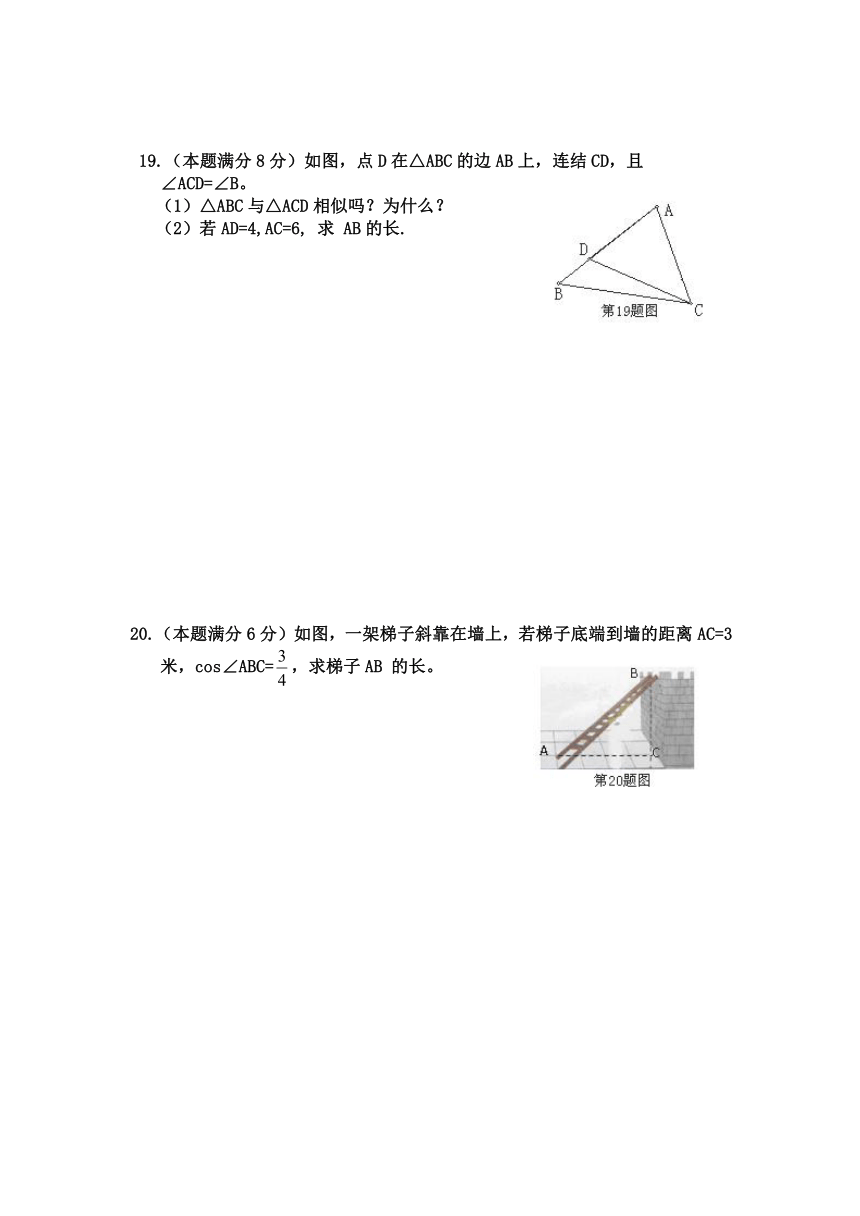
A. B. C. D.
3.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A. 带①去 B.带②去 C.带③去 D.带①和②去
4.若,则的值为( )
A.8 B.2 C.5 D.
5.计算的结果为( )
A.3 B.9 C.1 D.
6.如图,在△ABC和△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )
A.∠B=∠E,BC=EF B.BC=EF,AC=DF
C.∠A=∠D,∠B=∠E D.∠A=∠D, BC=EF
7.在,若将各边长都扩大为原来的2倍,则∠A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.不变
8.如图,选项中的阴影三角形与△ABC相似的为( )
9.下列根式中最简二次根式是( )
A. B. C. D.
10.如图,点D在AB上,点E在AC上,且∠B=∠C,
则在下列条件中,无法判定△ABE≌△ACD的是( )
A.AD=AE B.AB=AC
C.BE=CD D.∠AEB=∠ADC
11.若最简二次根式是同类二次根式,则a的值为( )
A. B. C. D.
12.如图,已知D、E分别是的AB、 AC边上的点,且=1:8,那么等于( )
A.1 : 9 B.1 : 3 C.1 : 8 D.1 : 2
二、填空题(将最后结果填在答卷的相应位置。本题共5个小题,每小题3分,共15分)
13.如果二次根式有意义,则x的范围是 .
14.一个五边形的边长分别是2、3、4、5、6,另一个和它相似的五边形的最短边长为6,则这个五边形的最长边为 。
15.如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从甲走到距路灯乙底部4米处时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.6米,那么路灯甲的高为 米.
16.如图,△ABC中,DE∥FG∥BC,图中有 对三角形相似.
17.如图,Rt△ABC中,斜边BC上的高AD=3,cosB=,则AC= .
2011~2012学年度第二学期八年级数学期中检测答卷
(时间120分钟,满分120分)
题号 一 二 三 总分
18 19 20 21 22 23 24
得分
一、选择题(每小题4分,共48分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(每题3分,共15分)
13. ; 14. ; 15. ;
16. ; 17. 。
三、解答题(本题共8个小题,共57分.解答应写出必要的文字说明、计算过程或推演步骤)
18.(本题满分12分)
(1)-+ ; (2);
(3); (4)。
19.(本题满分8分)如图,点D在△ABC的边AB上,连结CD,且
∠ACD=∠B。
(1)△ABC与△ACD相似吗?为什么?
(2)若AD=4,AC=6, 求 AB的长.
20.(本题满分6分)如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠ABC=,求梯子AB 的长。
21.(本题满分8分)已知,如图,点在同一直线上,,,CE=BF.
(1)△ACB与△DFE全等吗?为什么?
(2) AB与DE平行吗?为什么?
22.(本题满分7分)如图,有一把剪刀,AB=2BC,DB=2BE,剪刀前面有一长方体,宽PQ=12cm,想用剪刀的A、D两点夹住P、Q两点,那么手握的地方CE至少要张开多少?
23.(本题满分8分)先观察下列等式,再回答问题。
①=1+-=1; ②=1+-;
③=1+。
(1)根据上面三个等式提供的信息,请猜想的结果,并进行验证;
(2)按照上面各等式反映的规律,试写出用n(n为正整数)表示的等式.
24.(本题满分8分)如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
(1)ΔASR和ΔABC是否相似?为什么?
(2)试求正方形PQRS的边长。
2011~2012学年度第二学期八年级数学期中检测参考答案
一、选择题(每小题4分,共48分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 A C C A C D D B C D C B
二、填空题(每小题3分,共15分)
13.x≤2,且x≠0;14.18 ; 15.8 ; 16.3 ; 17.。
三、解答题:(本题共8个小题,共57分)
18.(本题满分12分) (1) ;(2);(3);(4)4。(每小题计算对得3分,共12分)
22. (本题满分7分)解:∵AB=2BC,DB=2BE,∴。……2分
∵∠ABD=∠CBE,∴△ABC∽△ACD. ……4分
∴,当AD=PQ=12时,CE=6cm. ……7分
23.(本题满分8分)(1)= 1+。……4分
(2)==1。……8分
选择题(本题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项符合题目要求,请把正确选项的序号填在答卷的相应位置)
1.计算的结果是( )
A.3 B. C. D.9
2.三角形在正方形网格纸中的位置如图所示,
则sinα的值是( )
A. B. C. D.
3.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A. 带①去 B.带②去 C.带③去 D.带①和②去
4.若,则的值为( )
A.8 B.2 C.5 D.
5.计算的结果为( )
A.3 B.9 C.1 D.
6.如图,在△ABC和△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )
A.∠B=∠E,BC=EF B.BC=EF,AC=DF
C.∠A=∠D,∠B=∠E D.∠A=∠D, BC=EF
7.在,若将各边长都扩大为原来的2倍,则∠A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.不变
8.如图,选项中的阴影三角形与△ABC相似的为( )
9.下列根式中最简二次根式是( )
A. B. C. D.
10.如图,点D在AB上,点E在AC上,且∠B=∠C,
则在下列条件中,无法判定△ABE≌△ACD的是( )
A.AD=AE B.AB=AC
C.BE=CD D.∠AEB=∠ADC
11.若最简二次根式是同类二次根式,则a的值为( )
A. B. C. D.
12.如图,已知D、E分别是的AB、 AC边上的点,且=1:8,那么等于( )
A.1 : 9 B.1 : 3 C.1 : 8 D.1 : 2
二、填空题(将最后结果填在答卷的相应位置。本题共5个小题,每小题3分,共15分)
13.如果二次根式有意义,则x的范围是 .
14.一个五边形的边长分别是2、3、4、5、6,另一个和它相似的五边形的最短边长为6,则这个五边形的最长边为 。
15.如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从甲走到距路灯乙底部4米处时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.6米,那么路灯甲的高为 米.
16.如图,△ABC中,DE∥FG∥BC,图中有 对三角形相似.
17.如图,Rt△ABC中,斜边BC上的高AD=3,cosB=,则AC= .
2011~2012学年度第二学期八年级数学期中检测答卷
(时间120分钟,满分120分)
题号 一 二 三 总分
18 19 20 21 22 23 24
得分
一、选择题(每小题4分,共48分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(每题3分,共15分)
13. ; 14. ; 15. ;
16. ; 17. 。
三、解答题(本题共8个小题,共57分.解答应写出必要的文字说明、计算过程或推演步骤)
18.(本题满分12分)
(1)-+ ; (2);
(3); (4)。
19.(本题满分8分)如图,点D在△ABC的边AB上,连结CD,且
∠ACD=∠B。
(1)△ABC与△ACD相似吗?为什么?
(2)若AD=4,AC=6, 求 AB的长.
20.(本题满分6分)如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠ABC=,求梯子AB 的长。
21.(本题满分8分)已知,如图,点在同一直线上,,,CE=BF.
(1)△ACB与△DFE全等吗?为什么?
(2) AB与DE平行吗?为什么?
22.(本题满分7分)如图,有一把剪刀,AB=2BC,DB=2BE,剪刀前面有一长方体,宽PQ=12cm,想用剪刀的A、D两点夹住P、Q两点,那么手握的地方CE至少要张开多少?
23.(本题满分8分)先观察下列等式,再回答问题。
①=1+-=1; ②=1+-;
③=1+。
(1)根据上面三个等式提供的信息,请猜想的结果,并进行验证;
(2)按照上面各等式反映的规律,试写出用n(n为正整数)表示的等式.
24.(本题满分8分)如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,四边形PQRS是正方形.
(1)ΔASR和ΔABC是否相似?为什么?
(2)试求正方形PQRS的边长。
2011~2012学年度第二学期八年级数学期中检测参考答案
一、选择题(每小题4分,共48分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 A C C A C D D B C D C B
二、填空题(每小题3分,共15分)
13.x≤2,且x≠0;14.18 ; 15.8 ; 16.3 ; 17.。
三、解答题:(本题共8个小题,共57分)
18.(本题满分12分) (1) ;(2);(3);(4)4。(每小题计算对得3分,共12分)
22. (本题满分7分)解:∵AB=2BC,DB=2BE,∴。……2分
∵∠ABD=∠CBE,∴△ABC∽△ACD. ……4分
∴,当AD=PQ=12时,CE=6cm. ……7分
23.(本题满分8分)(1)= 1+。……4分
(2)==1。……8分
同课章节目录
