福建省福州市平潭县高中2020-2021学年高一下学期期末考试数学试题 Word版含答案解析
文档属性
| 名称 | 福建省福州市平潭县高中2020-2021学年高一下学期期末考试数学试题 Word版含答案解析 |
|
|
| 格式 | docx | ||
| 文件大小 | 600.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 00:00:00 | ||
图片预览




文档简介
平潭县高中2020-2021学年高一数学下学期期末考试卷
考试时间∶ 120 分钟满分∶ 150 分
一、单选题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案涂在答题卡上。)
1.设集合false,false,则( )
A. M=N B. false C. false D. false
2.己知x>2,那么false的最小值为( )
A.3 B. 4 C.5 D.6
3. 已知m,n是两条不同的直线,a,β是两个不同的平面,给出四个命题∶
①若a∩β=m,false, n⊥m,则a⊥β;
②若m⊥a,m⊥β,则a//β;
③若m⊥a,n⊥β, m⊥n,则a⊥β;
④若m//a, n//β, m//n,则a//β.
其中正确的命题是( )
A.①② B.②③. C.①④ D.②④
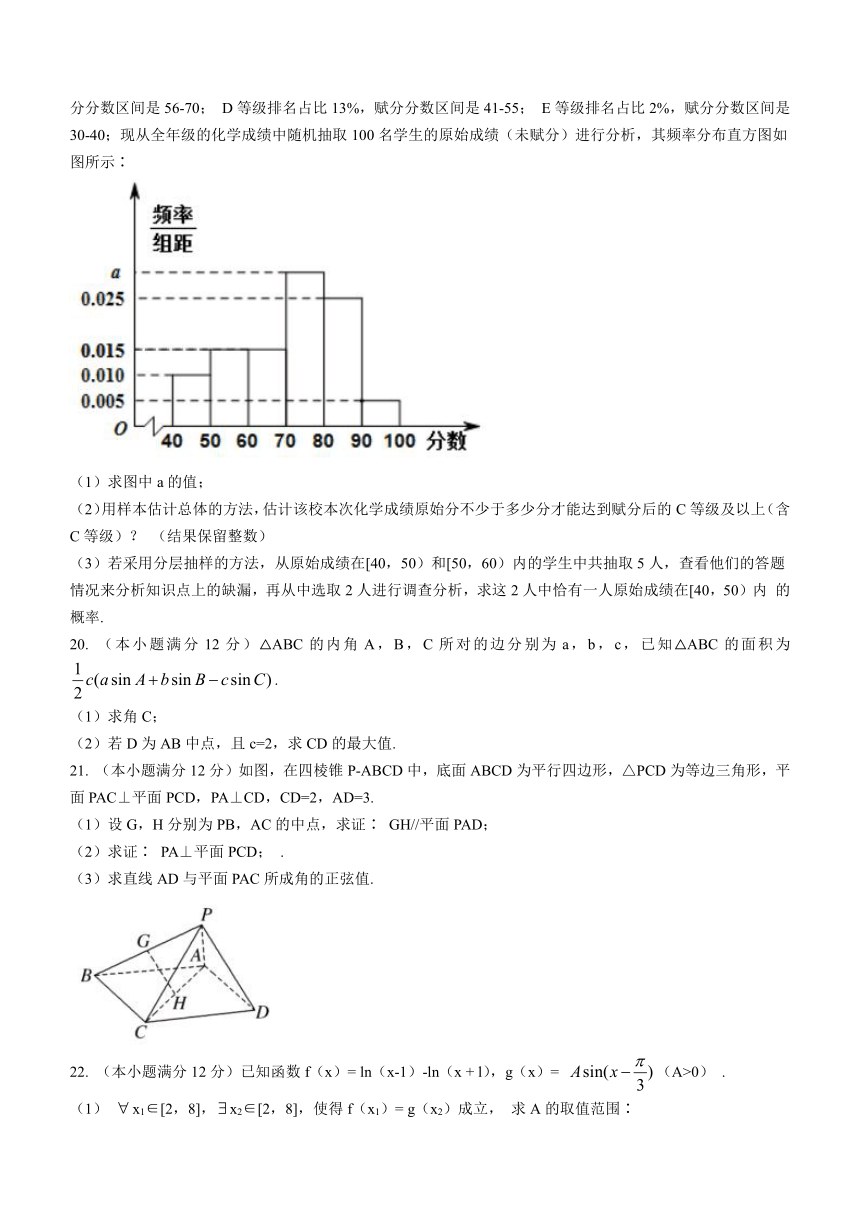
4.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高。如图是2018年9月到2019年2月这半年中,某个关键词的搜索指数变化的走势图.
根据该走势图,下列结论正确的是( )
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
5.在false中,BC=1,false,false,则A= ( )
A. false或false B. false C. false或false D. false
6.欧拉公式false(e为自然底数,i为虚数单位)是瑞士数学家欧拉最早发现的,是数学界最著名、最美丽的公式之一。根据欧拉公式,复数e2i在复平面内对应点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1, 则f(8)+f(9)等于( )
A.-2 B.-1 C. 0 D.1
8.设函数false,若函数g(x)= f(x)- ax恰有两个零点,则a的取值范围为( )
A. (0,2) B. (0,2] C. (2,+∞) D.[2,+∞)
二、多选题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对得3分,选错不得分。请将所选答案涂在答题卡上)
9.已知事件A,B,且P(A)=0.5,P(B)=0.2, 则下列结论正确的是( )
A.如果false,那么P(A∪B)=0.2,P(AB)=0.5
B.如果A与B互斥,那么P(AUB)=0.7,P(AB)=0
C.如果A与B相互独立,那么P(AUB)=0.7,P(AB)=0
D.如果A与B相互独立,那么false,false
10.设z1,z2,z3为复数,z1≠0,下列命题中正确的是( )
A.若|z2|=|z3|, 则z2=z3 B.若false,则z2=z3
C.若false, 则false D.若false,则false
11. 己知函数false,将f (x)图像上每一点的横坐标缩短到原来的false(纵坐标不变),得到函数g (x)的图像,则( )
A.当false时,g (x) 取最小值
B.g(x)在false上单调递减
C.g(x)的图像向左平移false个单位后对应的函数是偶函数
D.直线false与g (x)false图像的所有交点的横坐标之和为false
12.在棱长为2的正方体false中,点E, F分别是棱BC、CC1的中点,则下列结论正确的是( )
A.A1D⊥AF
B.三棱锥A-BCF外接球的表面积为9π
C.点C到平面AEF的距离为false
D.平面AEF截正方体所得的截面面积为false
三、填空题(本大题共4小题,每小题5分,共20分)
13. 设向量a=(1,2), b=(2,3), 若向量false与向量c=(-4,-7)共线,则λ=_ 。
14.计算∶false =_ 。
15.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量变为原来的一半所经历的时间称为它的半衰期,记为false。现测得某种放射性元素的剩余质量A随时间t变化的6次数据如下∶
t(单位时间)
0
2
4
6
8
10
A(t)
320
226
160
115
80
57
从以上记录可知这种元素的半衰期约为_ 个单位时间,剩余质量随时间变化的衰变公式为A(t)=_ 。
16.在三棱锥S- ABC中,△ABC是边长为3的等边三角形,false,false, 二面角S-AB-C的大小为120°,则此三棱锥的外接球的表面积为_ 。
四、解答题(本小题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。)
17. (本小题满分10分)已知向量false与false的夹角false,且false,false.
(1)求false,false在false上的投影向量;
(2)求向量false与false夹角的余弦值.
18. (本小题满分 12分)已知函数false
(1)求f (x)的最小正周期和单调递增区间;
(2)若false,且false,求cosA的值.
19. (本小题满分12分) 2021年起,福建省将实行“3+1+2"高考模式, 为让学生适应新高考的赋分模式某校在一次校考中使用赋分制给高三年级学生的化学成绩进行赋分,具体赋分方案如下∶先按照考生原始分从高到低按比例划定A、B、C、D、E共五个等级,然后在相应赋分区间内利用转换公式进行赋分A等级排名占比15%,赋分分数区间是86-100; B等级排名占比35%,赋分分数区间是71-85; C等级排名占比35%,赋分分数区间是56-70; D等级排名占比13%,赋分分数区间是41-55; E等级排名占比2%,赋分分数区间是30-40;现从全年级的化学成绩中随机抽取100名学生的原始成绩(未赋分)进行分析,其频率分布直方图如图所示∶
(1)求图中a的值;
(2)用样本估计总体的方法,估计该校本次化学成绩原始分不少于多少分才能达到赋分后的C等级及以上(含C等级)? (结果保留整数)
(3)若采用分层抽样的方法,从原始成绩在[40,50)和[50,60)内的学生中共抽取5人,查看他们的答题情况来分析知识点上的缺漏,再从中选取2人进行调查分析,求这2人中恰有一人原始成绩在[40,50)内 的概率.
20. (本小题满分12分)△ABC的内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为false.
(1)求角C;
(2)若D为AB中点,且c=2,求CD的最大值.
21. (本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.
(1)设G,H分别为PB,AC的中点,求证∶ GH//平面PAD;
(2)求证∶ PA⊥平面PCD; .
(3)求直线AD与平面PAC所成角的正弦值.
22. (本小题满分12分)已知函数f(x)= ln(x-1)-ln(x + l),g(x)= false(A>0) .
(1) falsex1∈[2,8],falsex2∈[2,8],使得f(x1)= g(x2)成立, 求A的取值范围∶
(2)若α,β∈(1,+∞),函数f(x)在区间[α,B]上的值域为false,false,且满足g(9m)=0,求m的值.
参考答案∶
1. [答案] C解析∶由x+3>0得x>-3,所以M= {x|x>-3}, 所以false,故选C.
2. [答案] D
3. [答案] B解析∶两个平面斜交时也会出现一个平面内的直线垂直于两个平面的交线的情况,①不正确;垂直于同一条直线的两个平面平行,②正确;当两个平面与两条互相垂直的直线分别垂直时,它们所成的二面角为直二面角,故③正确;当两个平面相交时,分别与两个平面平行的直线也平行,故④不正确.故选B。
4..[答案]D
[详解]
对于A,并无周期变化,故A错,
对于B,并不是不断减弱,中间有增强。故B错,
对于C,10月份的波动大小大于11月份,所以方差要大.故C错,
对于D,由图可知,12月起到1月份有下降的趋势,所以去年12月份的平均值大于今年1月份的平均值、故D正确,
5. [答案] B
[解析]
由正弦定理得false,∴false,
因为0因为BC=1所以A6. [答案] B
[详解]
由题意知∶false,而false,
∴cos2<0,sin2>0, 故false对应点在第二象限.
7.[ 答案] D
8. [答案] A
解析∶如图
9.[答案] BD
[解析] A选项∶如果false,那么false,P(AB)=0.2, 故A选项错误;
B选项∶如果A与B互斥,那么P(A∪B)=0.7,P(AB)=0, 故B选项正确∶
C选项∶如果A与B相互独立,那么P(A∪B)=0.7,P(AB)=0.1, 故C选项错误; .
D选项∶如果A与B相互独立,那么false,false,故D选项正确.
10. [答案] BC
解析∶
设false,false, false, 若false, 则false,此时false不一定成立,故A错误;
若false,则false, 又因false, 所以false,故B正确;
若false,则false,false,
所以false
所以false,故C正确;
当false时,false,此时false不一定成立,故D错误.
11. [答案] ACD
[解析]由条件可知false
当false时,false,此时g(x)=-1,取得最小值,所以A正确;
当false时,false,当false,即false,此时函数单调递减,当false,即false时,函数单调递增,故B不正确;g(x)向左平移false个单位后得到函数false,函数偶函数, 故C正确;
false,解得∶false,k∈Z, 解得∶false ,k∈Z或false,k∈Z,解得∶false,k∈Z,
因为false,所以false或false,
所以交点的横坐标之和为false,故D正确.
12. [ 答案] BCD
[解析]
A.如图,取DD1中点G,连接GF,GA,由于F是CC1中点,∴GF//DC,而DC⊥平面ADD1A1,∴GF⊥平面ADD1A1,A1D false平面ADD1A1, ∴.GF⊥A1D,若AP⊥AF,由于false,∴.A1D⊥平面AFG,又AG false平面AFG,∴A1D⊥AG,
但正方形ADD1A1中,G是DD1中点,不可能有A1D⊥AG, A错;
B.设AC与BD交于点M ,则M是△BC的外心,取AF中点N ,连接NM ,则NM //CF,
∴NM⊥平面ABCD,∴N是三棱锥A-BCF外接球的球心,
false,球表面积为false,B正确;
C. false,false
false中,false,false,AF=3,
则false,false
false,设C到平面AEF的距离为h,
则false得false,false ,C正确;
D.连接FD1,D1A,,易证得AD1 //BC1 // EF,平面AEF截正方体所得的截面即为等腰梯形AD1FE,false,false,false,梯形的高为false ,false, D正确.
13. 解析∶因为a=(1,2), b=(2,3), 所以λa+b=(λ, 2λ)+(2,3)=(n+2,2λ+3).
因为向量λa+b与向量c=(-4,- 7)共线,
所以-7(λ+ 2)+4(2λ+3)=0.所以λ=2.
答案∶ 2
14.解析∶原式=false
false
答案∶false
15.解析∶从题表中数据易知半衰期为4个单位时间,由初始质量为A0= 320, 则经过时间t的剩余质量为false.
答案∶ 4 false
16.解∶如图,因为AB=3,false, false,
所以false.
所以AS⊥BS,
取AB的中点D,BS的中点O1,连结O1D,CD,
则O1为△SAB的外心,O1D⊥AB,false
因为△ABC是边长为3的等边三角形,
所以其外心(记为O2 )在CD上,且O2D⊥AB,false
所以∠O1DO2就是二面角S- AB -C的平面角,
所以∠O1DO2 =120°
设外三棱锥S - ABC接球的球心为O,连结OO1,OO2,
则false,
所以由平面几何知识可知得false
所以false
所以三棱锥S - ABC的外接球表面积为false.
17. [答案](1)false,false,false在false上的投影向量为∶ false; (2)false
[详解]
(1)false,所以false
false, 所以false
false在false上的投影向量为∶false
(2)false
设向量false与false夹角为false,则false
18. [答案] (1) T=π,单调增区间为false, (2)false
[解析](1) false
false
false
所以f(x)的最小正周期为false,
由false,得false(k∈Z),
所以f(x)的单调增区间为false(k∈Z),
(2) 因为false,所以false
因为false,所以false
所以false
所以false
false
false
19. [答案] (1) a=0.030; (2) 54分; (3)false
[详解]
(1) 由题意,(0.010+0.015+0.015+a+0.025+0.005)*10=1, 所以a=0.030;
(2)由已知等级达到C及以上所占排名等级占比为15%+35%+35%=85%,
假设原始分不少于x分可以达到赋分后的C等级及以上,易得50则有(0.005 0.025 0.030 0.015) 10 (60 x) 0.015 0.85, 解 得x≈53.33(分),
所以原始分不少于54分才能达到赋分后的C等级及以上;
(3)由题知得分在[40,50)和[50,60)内的频率分别为0.1和0.15,
则抽取的5人中,得分在[40,50)内的有2人,得分在[50,60)的有3人
记得分在[50,60)内的3位学生为a, b, c,得分在[40,50)内的2位学生为D, E,
则从5人中任选2人,样本空间可记为
{ab, ac, aD, aE, bc, bD, bE,cD, cE,DE},共包含10 个样本
用A表示“这2人中恰有一人得分在[40,50)内”,
则A {aD, aE, bD, bE, cD, cE},A包含6个样本, .
故所求概率false
20.解法一∶ (1)依题意得,false,........... 分
由正弦定理得,false,即false,...............分
由余弦定理得,false
又因为false,所以false
(2)在△ACD中,
false,即false,
在△BCD中,
false,即false .
因为∠ADC+∠BDC=π,所以cos∠ADC=-cos∠BDC,
所以false. .........................分
由(1)及c=2得,false,所以false,
所以false,即false,.......................分
当且仅当a=b=2时,等号成立。....
所以CD的最大值为false. ................................... 分.
解法二∶ (1)同解法一,.................................... 分
(2)因为false,c=2,
所以false..2ab-4,即ab,, 4. ......................分
因为D为AB中点,所以false,
所以false......
false
false
false....10分
当且仅当a=b=2时,等号成立. ........................ 11分
所以CD的最大值为false. ....
21.解∶ (1)证明∶连接BD,易知false, BH=DH.
又由BG=PG,故GH// PD.
又因为false平面PAD,false平面PAD,所以GH//平面PAD.
(2)证明∶取棱PC的中点N,连接DN.依题意,得DN⊥PC.
又因为平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,
所以DN⊥平面PAC.
又false平面PAC,所以DN⊥PA.
又已知PA⊥CD, false,
所以PA⊥平面PCD.
(3)连接AN,由(2)中 DN⊥平面PAC,可知∠DAN为直线AD
与平面PAC所成的角.
因为△PCD为等边三角形,CD=2且N为PC的中点,
所以DN=false
又DN⊥AN,在false中,false.
所以,直线AD与平面PAC所成角的正弦值为false
22. [解答](1)false
其定义域为(1, +∞).
任取false∈(1,+∞),不妨设false,则
false
false’
因为falsex2)<0,
又false
所以false,所以f(x1)- f(x2)=
false,即false,
所以f(x)在(1, +∞)上为增函数.
故当x∈[2,8]时,false
当x∈[2,8]时,false,
所以false
①当A>0时,g(x2)的值域为[- A,A];
②当A<0时,g(x2 )的值域为[A,-A].
由题意知f(x1)的值域是g(x2 )的值域的子集,
则false
解得false
(2)由(1)知f(x)在(1,十∞).上为增函数,函数
f(x)在[a,β]上的值域为false,
false,
所以m>0,且false,
所以false
即a,β是方程false.的两个实数根,
问题等价于方程false在
x∈(1, +∞).上有两个不相等的实数根.
令false,其图像的对称轴为直线false,
则false
即false,
解得false
则false,从而由false
false,得false,则false
考试时间∶ 120 分钟满分∶ 150 分
一、单选题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案涂在答题卡上。)
1.设集合false,false,则( )
A. M=N B. false C. false D. false
2.己知x>2,那么false的最小值为( )
A.3 B. 4 C.5 D.6
3. 已知m,n是两条不同的直线,a,β是两个不同的平面,给出四个命题∶
①若a∩β=m,false, n⊥m,则a⊥β;
②若m⊥a,m⊥β,则a//β;
③若m⊥a,n⊥β, m⊥n,则a⊥β;
④若m//a, n//β, m//n,则a//β.
其中正确的命题是( )
A.①② B.②③. C.①④ D.②④
4.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高。如图是2018年9月到2019年2月这半年中,某个关键词的搜索指数变化的走势图.
根据该走势图,下列结论正确的是( )
A.这半年中,网民对该关键词相关的信息关注度呈周期性变化
B.这半年中,网民对该关键词相关的信息关注度不断减弱
C.从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D.从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
5.在false中,BC=1,false,false,则A= ( )
A. false或false B. false C. false或false D. false
6.欧拉公式false(e为自然底数,i为虚数单位)是瑞士数学家欧拉最早发现的,是数学界最著名、最美丽的公式之一。根据欧拉公式,复数e2i在复平面内对应点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.已知奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1, 则f(8)+f(9)等于( )
A.-2 B.-1 C. 0 D.1
8.设函数false,若函数g(x)= f(x)- ax恰有两个零点,则a的取值范围为( )
A. (0,2) B. (0,2] C. (2,+∞) D.[2,+∞)
二、多选题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对得3分,选错不得分。请将所选答案涂在答题卡上)
9.已知事件A,B,且P(A)=0.5,P(B)=0.2, 则下列结论正确的是( )
A.如果false,那么P(A∪B)=0.2,P(AB)=0.5
B.如果A与B互斥,那么P(AUB)=0.7,P(AB)=0
C.如果A与B相互独立,那么P(AUB)=0.7,P(AB)=0
D.如果A与B相互独立,那么false,false
10.设z1,z2,z3为复数,z1≠0,下列命题中正确的是( )
A.若|z2|=|z3|, 则z2=z3 B.若false,则z2=z3
C.若false, 则false D.若false,则false
11. 己知函数false,将f (x)图像上每一点的横坐标缩短到原来的false(纵坐标不变),得到函数g (x)的图像,则( )
A.当false时,g (x) 取最小值
B.g(x)在false上单调递减
C.g(x)的图像向左平移false个单位后对应的函数是偶函数
D.直线false与g (x)false图像的所有交点的横坐标之和为false
12.在棱长为2的正方体false中,点E, F分别是棱BC、CC1的中点,则下列结论正确的是( )
A.A1D⊥AF
B.三棱锥A-BCF外接球的表面积为9π
C.点C到平面AEF的距离为false
D.平面AEF截正方体所得的截面面积为false
三、填空题(本大题共4小题,每小题5分,共20分)
13. 设向量a=(1,2), b=(2,3), 若向量false与向量c=(-4,-7)共线,则λ=_ 。
14.计算∶false =_ 。
15.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量变为原来的一半所经历的时间称为它的半衰期,记为false。现测得某种放射性元素的剩余质量A随时间t变化的6次数据如下∶
t(单位时间)
0
2
4
6
8
10
A(t)
320
226
160
115
80
57
从以上记录可知这种元素的半衰期约为_ 个单位时间,剩余质量随时间变化的衰变公式为A(t)=_ 。
16.在三棱锥S- ABC中,△ABC是边长为3的等边三角形,false,false, 二面角S-AB-C的大小为120°,则此三棱锥的外接球的表面积为_ 。
四、解答题(本小题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。)
17. (本小题满分10分)已知向量false与false的夹角false,且false,false.
(1)求false,false在false上的投影向量;
(2)求向量false与false夹角的余弦值.
18. (本小题满分 12分)已知函数false
(1)求f (x)的最小正周期和单调递增区间;
(2)若false,且false,求cosA的值.
19. (本小题满分12分) 2021年起,福建省将实行“3+1+2"高考模式, 为让学生适应新高考的赋分模式某校在一次校考中使用赋分制给高三年级学生的化学成绩进行赋分,具体赋分方案如下∶先按照考生原始分从高到低按比例划定A、B、C、D、E共五个等级,然后在相应赋分区间内利用转换公式进行赋分A等级排名占比15%,赋分分数区间是86-100; B等级排名占比35%,赋分分数区间是71-85; C等级排名占比35%,赋分分数区间是56-70; D等级排名占比13%,赋分分数区间是41-55; E等级排名占比2%,赋分分数区间是30-40;现从全年级的化学成绩中随机抽取100名学生的原始成绩(未赋分)进行分析,其频率分布直方图如图所示∶
(1)求图中a的值;
(2)用样本估计总体的方法,估计该校本次化学成绩原始分不少于多少分才能达到赋分后的C等级及以上(含C等级)? (结果保留整数)
(3)若采用分层抽样的方法,从原始成绩在[40,50)和[50,60)内的学生中共抽取5人,查看他们的答题情况来分析知识点上的缺漏,再从中选取2人进行调查分析,求这2人中恰有一人原始成绩在[40,50)内 的概率.
20. (本小题满分12分)△ABC的内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为false.
(1)求角C;
(2)若D为AB中点,且c=2,求CD的最大值.
21. (本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3.
(1)设G,H分别为PB,AC的中点,求证∶ GH//平面PAD;
(2)求证∶ PA⊥平面PCD; .
(3)求直线AD与平面PAC所成角的正弦值.
22. (本小题满分12分)已知函数f(x)= ln(x-1)-ln(x + l),g(x)= false(A>0) .
(1) falsex1∈[2,8],falsex2∈[2,8],使得f(x1)= g(x2)成立, 求A的取值范围∶
(2)若α,β∈(1,+∞),函数f(x)在区间[α,B]上的值域为false,false,且满足g(9m)=0,求m的值.
参考答案∶
1. [答案] C解析∶由x+3>0得x>-3,所以M= {x|x>-3}, 所以false,故选C.
2. [答案] D
3. [答案] B解析∶两个平面斜交时也会出现一个平面内的直线垂直于两个平面的交线的情况,①不正确;垂直于同一条直线的两个平面平行,②正确;当两个平面与两条互相垂直的直线分别垂直时,它们所成的二面角为直二面角,故③正确;当两个平面相交时,分别与两个平面平行的直线也平行,故④不正确.故选B。
4..[答案]D
[详解]
对于A,并无周期变化,故A错,
对于B,并不是不断减弱,中间有增强。故B错,
对于C,10月份的波动大小大于11月份,所以方差要大.故C错,
对于D,由图可知,12月起到1月份有下降的趋势,所以去年12月份的平均值大于今年1月份的平均值、故D正确,
5. [答案] B
[解析]
由正弦定理得false,∴false,
因为0
[详解]
由题意知∶false,而false,
∴cos2<0,sin2>0, 故false对应点在第二象限.
7.[ 答案] D
8. [答案] A
解析∶如图
9.[答案] BD
[解析] A选项∶如果false,那么false,P(AB)=0.2, 故A选项错误;
B选项∶如果A与B互斥,那么P(A∪B)=0.7,P(AB)=0, 故B选项正确∶
C选项∶如果A与B相互独立,那么P(A∪B)=0.7,P(AB)=0.1, 故C选项错误; .
D选项∶如果A与B相互独立,那么false,false,故D选项正确.
10. [答案] BC
解析∶
设false,false, false, 若false, 则false,此时false不一定成立,故A错误;
若false,则false, 又因false, 所以false,故B正确;
若false,则false,false,
所以false
所以false,故C正确;
当false时,false,此时false不一定成立,故D错误.
11. [答案] ACD
[解析]由条件可知false
当false时,false,此时g(x)=-1,取得最小值,所以A正确;
当false时,false,当false,即false,此时函数单调递减,当false,即false时,函数单调递增,故B不正确;g(x)向左平移false个单位后得到函数false,函数偶函数, 故C正确;
false,解得∶false,k∈Z, 解得∶false ,k∈Z或false,k∈Z,解得∶false,k∈Z,
因为false,所以false或false,
所以交点的横坐标之和为false,故D正确.
12. [ 答案] BCD
[解析]
A.如图,取DD1中点G,连接GF,GA,由于F是CC1中点,∴GF//DC,而DC⊥平面ADD1A1,∴GF⊥平面ADD1A1,A1D false平面ADD1A1, ∴.GF⊥A1D,若AP⊥AF,由于false,∴.A1D⊥平面AFG,又AG false平面AFG,∴A1D⊥AG,
但正方形ADD1A1中,G是DD1中点,不可能有A1D⊥AG, A错;
B.设AC与BD交于点M ,则M是△BC的外心,取AF中点N ,连接NM ,则NM //CF,
∴NM⊥平面ABCD,∴N是三棱锥A-BCF外接球的球心,
false,球表面积为false,B正确;
C. false,false
false中,false,false,AF=3,
则false,false
false,设C到平面AEF的距离为h,
则false得false,false ,C正确;
D.连接FD1,D1A,,易证得AD1 //BC1 // EF,平面AEF截正方体所得的截面即为等腰梯形AD1FE,false,false,false,梯形的高为false ,false, D正确.
13. 解析∶因为a=(1,2), b=(2,3), 所以λa+b=(λ, 2λ)+(2,3)=(n+2,2λ+3).
因为向量λa+b与向量c=(-4,- 7)共线,
所以-7(λ+ 2)+4(2λ+3)=0.所以λ=2.
答案∶ 2
14.解析∶原式=false
false
答案∶false
15.解析∶从题表中数据易知半衰期为4个单位时间,由初始质量为A0= 320, 则经过时间t的剩余质量为false.
答案∶ 4 false
16.解∶如图,因为AB=3,false, false,
所以false.
所以AS⊥BS,
取AB的中点D,BS的中点O1,连结O1D,CD,
则O1为△SAB的外心,O1D⊥AB,false
因为△ABC是边长为3的等边三角形,
所以其外心(记为O2 )在CD上,且O2D⊥AB,false
所以∠O1DO2就是二面角S- AB -C的平面角,
所以∠O1DO2 =120°
设外三棱锥S - ABC接球的球心为O,连结OO1,OO2,
则false,
所以由平面几何知识可知得false
所以false
所以三棱锥S - ABC的外接球表面积为false.
17. [答案](1)false,false,false在false上的投影向量为∶ false; (2)false
[详解]
(1)false,所以false
false, 所以false
false在false上的投影向量为∶false
(2)false
设向量false与false夹角为false,则false
18. [答案] (1) T=π,单调增区间为false, (2)false
[解析](1) false
false
false
所以f(x)的最小正周期为false,
由false,得false(k∈Z),
所以f(x)的单调增区间为false(k∈Z),
(2) 因为false,所以false
因为false,所以false
所以false
所以false
false
false
19. [答案] (1) a=0.030; (2) 54分; (3)false
[详解]
(1) 由题意,(0.010+0.015+0.015+a+0.025+0.005)*10=1, 所以a=0.030;
(2)由已知等级达到C及以上所占排名等级占比为15%+35%+35%=85%,
假设原始分不少于x分可以达到赋分后的C等级及以上,易得50
所以原始分不少于54分才能达到赋分后的C等级及以上;
(3)由题知得分在[40,50)和[50,60)内的频率分别为0.1和0.15,
则抽取的5人中,得分在[40,50)内的有2人,得分在[50,60)的有3人
记得分在[50,60)内的3位学生为a, b, c,得分在[40,50)内的2位学生为D, E,
则从5人中任选2人,样本空间可记为
{ab, ac, aD, aE, bc, bD, bE,cD, cE,DE},共包含10 个样本
用A表示“这2人中恰有一人得分在[40,50)内”,
则A {aD, aE, bD, bE, cD, cE},A包含6个样本, .
故所求概率false
20.解法一∶ (1)依题意得,false,........... 分
由正弦定理得,false,即false,...............分
由余弦定理得,false
又因为false,所以false
(2)在△ACD中,
false,即false,
在△BCD中,
false,即false .
因为∠ADC+∠BDC=π,所以cos∠ADC=-cos∠BDC,
所以false. .........................分
由(1)及c=2得,false,所以false,
所以false,即false,.......................分
当且仅当a=b=2时,等号成立。....
所以CD的最大值为false. ................................... 分.
解法二∶ (1)同解法一,.................................... 分
(2)因为false,c=2,
所以false..2ab-4,即ab,, 4. ......................分
因为D为AB中点,所以false,
所以false......
false
false
false....10分
当且仅当a=b=2时,等号成立. ........................ 11分
所以CD的最大值为false. ....
21.解∶ (1)证明∶连接BD,易知false, BH=DH.
又由BG=PG,故GH// PD.
又因为false平面PAD,false平面PAD,所以GH//平面PAD.
(2)证明∶取棱PC的中点N,连接DN.依题意,得DN⊥PC.
又因为平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,
所以DN⊥平面PAC.
又false平面PAC,所以DN⊥PA.
又已知PA⊥CD, false,
所以PA⊥平面PCD.
(3)连接AN,由(2)中 DN⊥平面PAC,可知∠DAN为直线AD
与平面PAC所成的角.
因为△PCD为等边三角形,CD=2且N为PC的中点,
所以DN=false
又DN⊥AN,在false中,false.
所以,直线AD与平面PAC所成角的正弦值为false
22. [解答](1)false
其定义域为(1, +∞).
任取false∈(1,+∞),不妨设false,则
false
false’
因为falsex2)<0,
又false
所以false,所以f(x1)- f(x2)=
false,即false,
所以f(x)在(1, +∞)上为增函数.
故当x∈[2,8]时,false
当x∈[2,8]时,false,
所以false
①当A>0时,g(x2)的值域为[- A,A];
②当A<0时,g(x2 )的值域为[A,-A].
由题意知f(x1)的值域是g(x2 )的值域的子集,
则false
解得false
(2)由(1)知f(x)在(1,十∞).上为增函数,函数
f(x)在[a,β]上的值域为false,
false,
所以m>0,且false,
所以false
即a,β是方程false.的两个实数根,
问题等价于方程false在
x∈(1, +∞).上有两个不相等的实数根.
令false,其图像的对称轴为直线false,
则false
即false,
解得false
则false,从而由false
false,得false,则false
同课章节目录
