11.3.1 多边形 课时达标检测(含解析)
文档属性
| 名称 | 11.3.1 多边形 课时达标检测(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年八年级上册数学同步练习卷
11.3多边形及其内角和
11.3.1 多边形
一、单选题
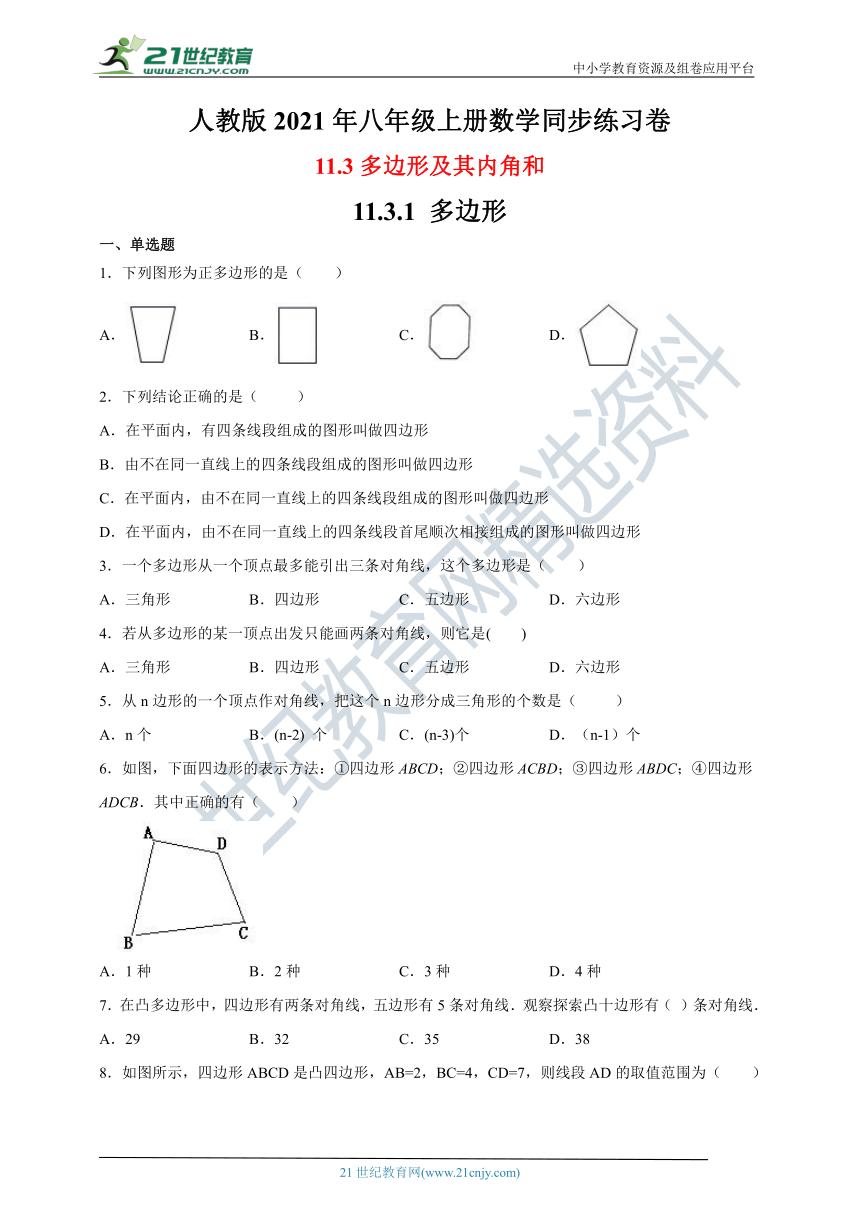
1.下列图形为正多边形的是( )
A. B. C. D.
2.下列结论正确的是( )
A.在平面内,有四条线段组成的图形叫做四边形
B.由不在同一直线上的四条线段组成的图形叫做四边形
C.在平面内,由不在同一直线上的四条线段组成的图形叫做四边形
D.在平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形
3.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.若从多边形的某一顶点出发只能画两条对角线,则它是( )
A.三角形 B.四边形 C.五边形 D.六边形
5.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n个 B.(n-2) 个 C.(n-3)个 D.(n-1)个
6.如图,下面四边形的表示方法:①四边形ABCD;②四边形ACBD;③四边形ABDC;④四边形ADCB.其中正确的有( )
A.1种 B.2种 C.3种 D.4种
7.在凸多边形中,四边形有两条对角线,五边形有5条对角线.观察探索凸十边形有( )条对角线.
A.29 B.32 C.35 D.38
8.如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( )
A.0<AD<7 B.2<AD<7 C.0<AD<13 D.1<AD<13
9.将已知六边形ABCDEF,用对角线将它剖分成互不重叠的4个三角形,那么各种不同的剖分方法种数是( )
A.6 B.8 C.12 D.14
10.下列属于正多边形的特征的有( )
(1)各边相等 (2)各个内角相等 (3)各个外角相等 (4)各条对角线都相等 (5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形
A.2个 B.3个 C.4个 D.5个
11.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A.三角形 B.四边形 C.五边形 D.六边形
12.如果一个多边形的内角和是720°,那么这个多边形的对角线的条数是( )
A.6 B.9 C.14 D.20
二、填空题
13.如果过多边形的一个顶点的所有对角线能将这个多边形分割成6个三角形,那么这个多边形是__________边形.
14.过四边形的一个顶点可以把四边形分成两个三角形;过五边形或六边形的一个顶点的对角线,可以分别把它们分成____________个三角形;过n边形的一个顶点的对角线可以把n边形分成_________个(用含n的代数式表示)三角形.
15.已知从多边形的一个顶点引出的对角线把多边形划分为10个三角形,则此多边形的内角和是____________
16.过四边形的一个顶点可以作________条对角线,可将四边形分割成________个三角形.
17.一个四边形它有_____条边,有_____个内角,有______个外角,从一个顶点出发可以引______条对角线,一共可以画______条对角线.
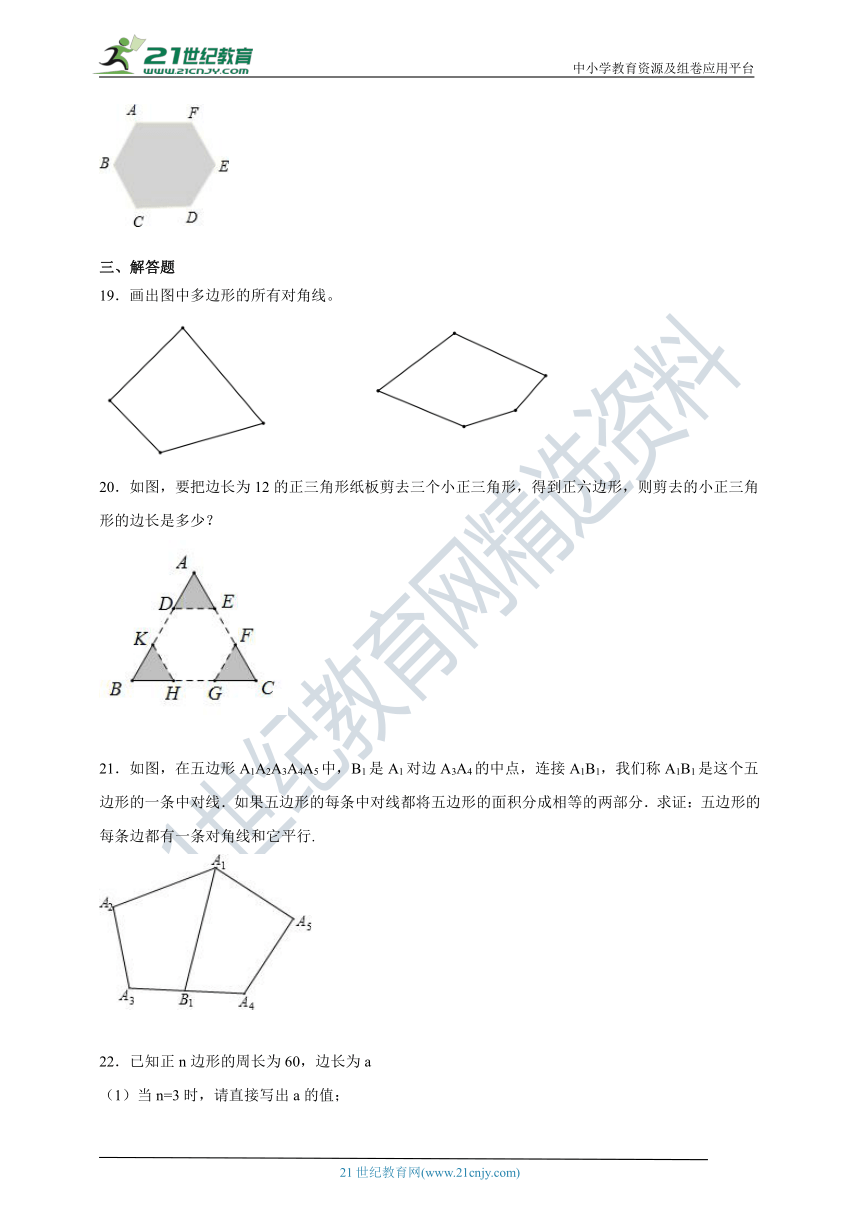
18.如图,在正六边形ABCDEF内放入2008个点,若这2008个点连同正六边形的六个顶点无三点共线,则该正六边形被这些点分成互不重合的三角形共_____个.
三、解答题
19.画出图中多边形的所有对角线。
20.如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长是多少?
21.如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连接A1B1,我们称A1B1是这个五边形的一条中对线.如果五边形的每条中对线都将五边形的面积分成相等的两部分.求证:五边形的每条边都有一条对角线和它平行.
22.已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
(1)如图(1),O为四边形ABCD内一点,连接OA、OB、OC、OC可以得几个三角形?它与边数有何关系?
如图(2),O在五边形ABCDE的AB上,连接OC、OD、OE,可以得到几个三角形?它与边数有何关系?
(3)如图(3),过A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
参考答案
1.D
【详解】
根据正多边形的定义,得到D中图形是正五边形.
2.D
【解析】
根据四边形的定义,由不在同一直线上四条线段依次首尾相接围成的封闭的平面图形叫做四边形,与每个选项一一比较,可知选项D是符合四边形的定义,
3.D
【详解】
试题分析:对于n边形,经过一个顶点能引出(n-3)条对角线,故本题选择D.
4.C
【详解】
解:设多边形有n条边,
则n-3=2,解得n=5.
故多边形的边数为5,即它是五边形.
5.B
【详解】
解:从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是(n-2).
故选B.
6.B
【详解】
根据题意,结合图形,
所给四边形的表示方法正确的有:
①四边形ABCD;④四边形ADCB.
7.C
【详解】
解:当n=10时,
,
即凸十边形的对角线有35条.
8.D
【解析】
连接AC,
∵AB=2,BC=4,
在△ABC中,根据三角形的三边关系,4?2∴?6在△ACD中,根据三角形的三边关系,得CD?AC∴19.D
【解析】
∵六边形ABCDEF有6个顶点,且用对角线将它剖分成互不重叠的4个三角形,
∴只能通过同一个顶点作三条对角线(如图1),这种分法有6种,
也从一个顶点作两条对角线(如图2),这种分法有2种,
如图3,中间是个四边形,两端2个三角形,把四边形加条对角线,这种分法有6种,
故各种不同的剖分方法有14种.
10.B
【解析】
①各边相等是正确的;
②各个内角相等是正确的;
③各个外角相等是正确的;
④各条对角线不一定相等,原来的说法是错误的;
⑤从一个顶点引出的对角线将n边形分成面积不一定相等的(n?2)个三角形,原来的说法是错误的.
故选B.
11.D
【详解】
当剪去一个角后,剩下的部分是一个四边形,
则这张纸片原来的形状可能是四边形或三角形或五边形,不可能是六边形.
故选D.
12.B
【详解】
设多边形的边数为n,则有:(n-2)?180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
13.八
【详解】
设多边形是边形,由对角线公式,得:
.
解得:,
故答案为:八.
14.3或4 n-2
【详解】
过五边形的一个顶点可以把五边形分成3个三角形,过六边形的一个顶点可以把六边形分成4个三角形;以此类推,过n边形的一个顶点的对角线可以把n边形分成(n-2)三角形.
故答案为3或4;n-2.
15.1800°
【详解】
解:10×180°=1800°,
故答案为:1800°.
16.1, 2
【详解】
解:过四边形的一个顶点出发可以引4-3=1条对角线,把四边形分割成4-2=2个三角形,
故答案为:1,2.
17.4 4 4 1 2
【解析】
根据四边形的定义得一个四边形它有4条边,有4个内角,有4个外角,从一个顶点出发可以引4-3=1条对角线,一共可以画=2条对角线.
18.4020
【解析】
∵正六边形ABCDEF内放入2008个点,这2008个点连同正六边形的六个顶点无三点共线,
∴共有2008+6=2014个点。
∵在正六边形内放入1个点时,该正六边形被这个点分成互不重合的三角形共6个;即当n=1时,有6个;然后出现第2个点时,这个点必然存在于开始的6个中的某一个三角形内,然后此点将那个三角形又分成3个三角形,三角形数量便增加2个;又出现第3个点时,同理,必然出现在某个已存在的三角形内,然后又将此三角形1分为3,增加2个…,
∴内部的点每增加1个,三角形个数便增加2个。
于是我们得到一个等差数列:存在n个点时,三角形数目an=a1+(n?1)d=6+2(n?1)=2n+4(n?1).
由题干知,2008个点的总数为a2008=2×2008+4=4020(个).
19.
解:分别将两个图形中的与每个顶点不相邻的顶点连接起来,如图:
20.4
【详解】
小正三角形和正六边形的各边都分别相等,且每个小正三角形与正六边形均有公共边,.
又
,
,
即剪去的小正三角形的边长是4.
21.证明见解析
【解析】
试题分析:此题要能够根据面积相等得到两条直线间的距离相等,从而证明两条直线平行;可以再作五边形的一条中对线,根据它们分割成的两部分的面积相等,都是五边形的面积的一半,导出两个等底的三角形的面积相等,从而得到它们的高相等,则得到五边形的每条边都有一条对角线和它平行.
试题解析:取A1A5中点B3,连接A3B3、A1A3、A1A4、A3A5,
∵A3B1=B1A4,
∴=,
又∵四边形A1A2A3B1与四边形A1B1A4A5的面积相等,
∴=,
同理=,
∴=,
∴△A3A4A5与△A1A4A5边A4A5上的高相等,
∴A1A3∥A4A5,
同理可证A1A2∥A3A5,A2A3∥A1A4,A3A4∥A2A5,A5A1∥A2A4.
点睛:此题主要考查多边形的有关知识,要能够根据面积相等得到两条直线间的距离相等,从而证明两条直线平行.
22.(1)20(2)不正确
【解析】
(1)根据正多边形的每条边相等,可知边长=周长÷边数;
(2)分别表示出a和b的代数式,让其相等,看是否有相应的值.
试题解析:(1)a=60÷3=20;
(2)此说法不正确.
理由如下:尽管当n=3、20、120时,a>b或a<b,
但可令a=b,得,
∴60n+420=67n,
解得n=60,
经检验n=60是方程的根.
∴当n=60时,a=b,即不符合这一说法的n的值为60.
23.(1)连接OA、OB、OC、OD可以得4个三角形,它与边数相等,
(2)连接OC、OD、OE可以得4个三角形,它的个数比边数小1,
(3)过点A作六边形ABCDEF的对角线,可以得到4个三角形,它的个数比边数小2.
【解析】
(1)根据图形可以得4个三角形,它与边数相等,
(2)根据图形可以得4个三角形,它的个数比边数小1,
(3)根据图形可以得到4个三角形,它的个数比边数小2.
_21?????????è?????(www.21cnjy.com)_
人教版2021年八年级上册数学同步练习卷
11.3多边形及其内角和
11.3.1 多边形
一、单选题
1.下列图形为正多边形的是( )
A. B. C. D.
2.下列结论正确的是( )
A.在平面内,有四条线段组成的图形叫做四边形
B.由不在同一直线上的四条线段组成的图形叫做四边形
C.在平面内,由不在同一直线上的四条线段组成的图形叫做四边形
D.在平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形
3.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
4.若从多边形的某一顶点出发只能画两条对角线,则它是( )
A.三角形 B.四边形 C.五边形 D.六边形
5.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n个 B.(n-2) 个 C.(n-3)个 D.(n-1)个
6.如图,下面四边形的表示方法:①四边形ABCD;②四边形ACBD;③四边形ABDC;④四边形ADCB.其中正确的有( )
A.1种 B.2种 C.3种 D.4种
7.在凸多边形中,四边形有两条对角线,五边形有5条对角线.观察探索凸十边形有( )条对角线.
A.29 B.32 C.35 D.38
8.如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( )
A.0<AD<7 B.2<AD<7 C.0<AD<13 D.1<AD<13
9.将已知六边形ABCDEF,用对角线将它剖分成互不重叠的4个三角形,那么各种不同的剖分方法种数是( )
A.6 B.8 C.12 D.14
10.下列属于正多边形的特征的有( )
(1)各边相等 (2)各个内角相等 (3)各个外角相等 (4)各条对角线都相等 (5)从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形
A.2个 B.3个 C.4个 D.5个
11.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A.三角形 B.四边形 C.五边形 D.六边形
12.如果一个多边形的内角和是720°,那么这个多边形的对角线的条数是( )
A.6 B.9 C.14 D.20
二、填空题
13.如果过多边形的一个顶点的所有对角线能将这个多边形分割成6个三角形,那么这个多边形是__________边形.
14.过四边形的一个顶点可以把四边形分成两个三角形;过五边形或六边形的一个顶点的对角线,可以分别把它们分成____________个三角形;过n边形的一个顶点的对角线可以把n边形分成_________个(用含n的代数式表示)三角形.
15.已知从多边形的一个顶点引出的对角线把多边形划分为10个三角形,则此多边形的内角和是____________
16.过四边形的一个顶点可以作________条对角线,可将四边形分割成________个三角形.
17.一个四边形它有_____条边,有_____个内角,有______个外角,从一个顶点出发可以引______条对角线,一共可以画______条对角线.
18.如图,在正六边形ABCDEF内放入2008个点,若这2008个点连同正六边形的六个顶点无三点共线,则该正六边形被这些点分成互不重合的三角形共_____个.
三、解答题
19.画出图中多边形的所有对角线。
20.如图,要把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长是多少?
21.如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连接A1B1,我们称A1B1是这个五边形的一条中对线.如果五边形的每条中对线都将五边形的面积分成相等的两部分.求证:五边形的每条边都有一条对角线和它平行.
22.已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
(1)如图(1),O为四边形ABCD内一点,连接OA、OB、OC、OC可以得几个三角形?它与边数有何关系?
如图(2),O在五边形ABCDE的AB上,连接OC、OD、OE,可以得到几个三角形?它与边数有何关系?
(3)如图(3),过A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
参考答案
1.D
【详解】
根据正多边形的定义,得到D中图形是正五边形.
2.D
【解析】
根据四边形的定义,由不在同一直线上四条线段依次首尾相接围成的封闭的平面图形叫做四边形,与每个选项一一比较,可知选项D是符合四边形的定义,
3.D
【详解】
试题分析:对于n边形,经过一个顶点能引出(n-3)条对角线,故本题选择D.
4.C
【详解】
解:设多边形有n条边,
则n-3=2,解得n=5.
故多边形的边数为5,即它是五边形.
5.B
【详解】
解:从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是(n-2).
故选B.
6.B
【详解】
根据题意,结合图形,
所给四边形的表示方法正确的有:
①四边形ABCD;④四边形ADCB.
7.C
【详解】
解:当n=10时,
,
即凸十边形的对角线有35条.
8.D
【解析】
连接AC,
∵AB=2,BC=4,
在△ABC中,根据三角形的三边关系,4?2
【解析】
∵六边形ABCDEF有6个顶点,且用对角线将它剖分成互不重叠的4个三角形,
∴只能通过同一个顶点作三条对角线(如图1),这种分法有6种,
也从一个顶点作两条对角线(如图2),这种分法有2种,
如图3,中间是个四边形,两端2个三角形,把四边形加条对角线,这种分法有6种,
故各种不同的剖分方法有14种.
10.B
【解析】
①各边相等是正确的;
②各个内角相等是正确的;
③各个外角相等是正确的;
④各条对角线不一定相等,原来的说法是错误的;
⑤从一个顶点引出的对角线将n边形分成面积不一定相等的(n?2)个三角形,原来的说法是错误的.
故选B.
11.D
【详解】
当剪去一个角后,剩下的部分是一个四边形,
则这张纸片原来的形状可能是四边形或三角形或五边形,不可能是六边形.
故选D.
12.B
【详解】
设多边形的边数为n,则有:(n-2)?180°=720°,解得:n=6,
所以这个多边形的对角线的条数是==9,
13.八
【详解】
设多边形是边形,由对角线公式,得:
.
解得:,
故答案为:八.
14.3或4 n-2
【详解】
过五边形的一个顶点可以把五边形分成3个三角形,过六边形的一个顶点可以把六边形分成4个三角形;以此类推,过n边形的一个顶点的对角线可以把n边形分成(n-2)三角形.
故答案为3或4;n-2.
15.1800°
【详解】
解:10×180°=1800°,
故答案为:1800°.
16.1, 2
【详解】
解:过四边形的一个顶点出发可以引4-3=1条对角线,把四边形分割成4-2=2个三角形,
故答案为:1,2.
17.4 4 4 1 2
【解析】
根据四边形的定义得一个四边形它有4条边,有4个内角,有4个外角,从一个顶点出发可以引4-3=1条对角线,一共可以画=2条对角线.
18.4020
【解析】
∵正六边形ABCDEF内放入2008个点,这2008个点连同正六边形的六个顶点无三点共线,
∴共有2008+6=2014个点。
∵在正六边形内放入1个点时,该正六边形被这个点分成互不重合的三角形共6个;即当n=1时,有6个;然后出现第2个点时,这个点必然存在于开始的6个中的某一个三角形内,然后此点将那个三角形又分成3个三角形,三角形数量便增加2个;又出现第3个点时,同理,必然出现在某个已存在的三角形内,然后又将此三角形1分为3,增加2个…,
∴内部的点每增加1个,三角形个数便增加2个。
于是我们得到一个等差数列:存在n个点时,三角形数目an=a1+(n?1)d=6+2(n?1)=2n+4(n?1).
由题干知,2008个点的总数为a2008=2×2008+4=4020(个).
19.
解:分别将两个图形中的与每个顶点不相邻的顶点连接起来,如图:
20.4
【详解】
小正三角形和正六边形的各边都分别相等,且每个小正三角形与正六边形均有公共边,.
又
,
,
即剪去的小正三角形的边长是4.
21.证明见解析
【解析】
试题分析:此题要能够根据面积相等得到两条直线间的距离相等,从而证明两条直线平行;可以再作五边形的一条中对线,根据它们分割成的两部分的面积相等,都是五边形的面积的一半,导出两个等底的三角形的面积相等,从而得到它们的高相等,则得到五边形的每条边都有一条对角线和它平行.
试题解析:取A1A5中点B3,连接A3B3、A1A3、A1A4、A3A5,
∵A3B1=B1A4,
∴=,
又∵四边形A1A2A3B1与四边形A1B1A4A5的面积相等,
∴=,
同理=,
∴=,
∴△A3A4A5与△A1A4A5边A4A5上的高相等,
∴A1A3∥A4A5,
同理可证A1A2∥A3A5,A2A3∥A1A4,A3A4∥A2A5,A5A1∥A2A4.
点睛:此题主要考查多边形的有关知识,要能够根据面积相等得到两条直线间的距离相等,从而证明两条直线平行.
22.(1)20(2)不正确
【解析】
(1)根据正多边形的每条边相等,可知边长=周长÷边数;
(2)分别表示出a和b的代数式,让其相等,看是否有相应的值.
试题解析:(1)a=60÷3=20;
(2)此说法不正确.
理由如下:尽管当n=3、20、120时,a>b或a<b,
但可令a=b,得,
∴60n+420=67n,
解得n=60,
经检验n=60是方程的根.
∴当n=60时,a=b,即不符合这一说法的n的值为60.
23.(1)连接OA、OB、OC、OD可以得4个三角形,它与边数相等,
(2)连接OC、OD、OE可以得4个三角形,它的个数比边数小1,
(3)过点A作六边形ABCDEF的对角线,可以得到4个三角形,它的个数比边数小2.
【解析】
(1)根据图形可以得4个三角形,它与边数相等,
(2)根据图形可以得4个三角形,它的个数比边数小1,
(3)根据图形可以得到4个三角形,它的个数比边数小2.
_21?????????è?????(www.21cnjy.com)_
