11.3.2 多边形内角和 课时达标检测(含解析)
文档属性
| 名称 | 11.3.2 多边形内角和 课时达标检测(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年八年级上册数学同步练习卷
11.3多边形及其内角和
11.3.2 多边形内角和
一、单选题
1.六边形的内角和为( )
A.360° B.540° C.720° D.180°
2.若一个正多边形的一个外角是45°,则这个正多边形的边数是( )
A.6 B.8 C.10 D.12
3.某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°”;乙说:“多边形的边数每增加1,则外角和增加180°”;丙说:“多边形的内角和不小于其外角和”;丁说:“只要是多边形,外角和都是360°”.你认为正确的是( )
A.甲和丁 B.乙和丙 C.丙和丁 D.以上都不对
4.下列说法正确的是( )
A.等腰三角形两边长为4,9,则三角形的周长为17或22
B.三角形的外角和为
C.在三角形,四边形,五边形中,只有三角形具有稳定性
D.四边形共有4条对角线
5.所有内角都相等的18边形,它的每个内角、外角的度数是( )
A.120°,60° B.140°,40° C.160°,20° D.100°,80°
6.设一个凸多边形,除去一个内角以外,其他内角的和为2570°,则该内角为( ).
A.40° B.90° C.120° D.130°
7.将正三角形、正四边形、正五边形按如图所示的位置摆放,如果,那么( )
A. B. C. D.
8.如图,正五边形ABCDE,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G=( )
A.36°
B.54°
C.60°
D.72°
9.如图,在中,,,,,连接BC,CD,则的度数是( )
A.45° B.50° C.55° D.80°
10.马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于,则该多边形的边数是( )
A.7 B.8 C.7或8 D.无法确定
11.如图,一束平行太阳光线FA、GB照射到正五边形ABCDE上,∠ABG=46°,则∠FAE的度数是( )
A.26°. B.44°. C.46°. D.72°
12.如图,小明从点出发,前进到点处后向右转20°,再前进到点处后又向右转20°,…,这样一直走下去,他第一次回到出发点时,一共走了( )
A. B. C. D.
二、填空题
13.如图,设、、是的外角,则____________.
14.一个多边形的内角和是 1440°,则这个多边形是__________边形.
15.如果一个多边形的边数由8变成9,其内角和增加了____________.
16.若一个正多边形的内角和比四边形的内角和多360°,则这个正多边形的每个内角的度数为___.
17.如图,在四边形ABCD中,.将沿MN翻折得到,若,则_____________.
18.四边形有2条对角线,五边形有5条对角线,六边形有9条对角线,……n边形有________条对角线.
三、解答题
19.如果一个多边形的内角和与外角和之比是 13:2,求这个多边形的边数.
已知正多边形的每个内角都是156°,求这个多边形的边数.
如果一个多边形的每一个外角都相等,且比内角小,求这个多边形的边数和内角和.
22.中,,点分别是边上的点,点是一动点,令,,.
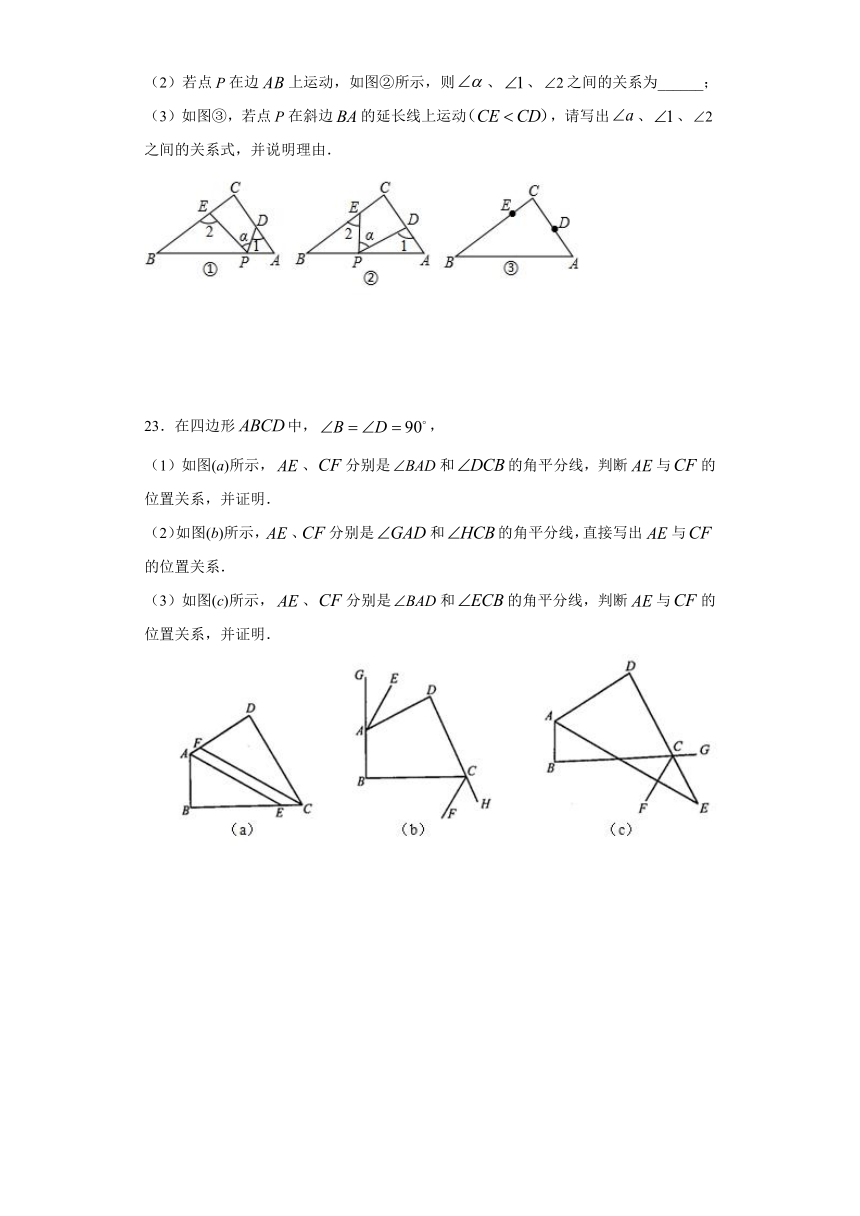
(1)若点在线段上,如图①所示,且,则_____;
(2)若点在边上运动,如图②所示,则、、之间的关系为______;
(3)如图③,若点在斜边的延长线上运动,请写出、、之间的关系式,并说明理由.
23.在四边形中,,
(1)如图(a)所示,、分别是和的角平分线,判断与的位置关系,并证明.
(2)如图(b)所示,、分别是和的角平分线,直接写出与的位置关系.
(3)如图(c)所示,、分别是和的角平分线,判断与的位置关系,并证明.
参考答案
1.C
【详解】
解:根据多边形的内角和可得:
六边形的内角和为(6﹣2)×180°=720°.
故选C.
2.B
【详解】
∵多边形外角和=360°,
∴这个正多边形的边数是360°÷45°=8.
故选:B.
3.A
【详解】
多边形的内角和公式为,n为多边形的边数
当n增加1,则内角和增加,甲说法正确
任意多边形的外角和都等于,则乙说法错误,丁说法正确
当时,多边形的内角和为,外角和为,则丙说法错误
综上,说法正确的是甲和丁
4.C
【详解】
A.等腰三角形两边长为4,9,当4为腰长时,,不满足三角形三边关系定理,三角形的周长为,错误;
B.三角形的外角和为,错误;
C.在三角形,四边形,五边形中,只有三角形具有稳定性,正确;
D.四边形共有2条对角线,错误.
5.C
【详解】
解:∵内角都相等,
∴每个外角也都相等,
∴每个外角为:,
则每个内角为:180°-20°=160°,
故答案为:C.
6.D
【详解】
解:∵2570°÷180°=14…50°,
∴该内角应是180°-50°=130°.
故选:D.
7.C
【详解】
解:如图所示,正三角形、正四边形、正五边形的每个内角的度数分别为,
∴中间阴影部分的三角形的三个外角的度数分别为,
∵三角形的外角和为,
∴.
,
8.B
【详解】
∵正五边形外角和为360°,∴外角,
∴内角,
∵BG平分∠ABC,DG平分正五边形的外角∠EDF
∴,
在四边形BCDG中,
∴
9.B
【详解】
解:连接AC并延长交EF于点M.
,
,
,
,
,
,
,
10.C
【详解】
设少加的2个内角和为x度,边数为n.
则(n-2)×180=830+x,
即(n-2)×180=4×180+110+x,
因此x=70,n=7或x=250,n=8.
故该多边形的边数是7或8.
11.A
【详解】
解:∵图中是正五边形.
∴∠EAB=108°.
∵太阳光线互相平行,∠ABG=46°,
∴∠FAE=180°﹣∠ABG﹣∠EAB=180°﹣46°﹣108°=26°.
12.C
【详解】
∵多边形的外角和等于360°,
∴ =18,
18×5m=90m,
13.360°
【详解】
解:∵三角形的外角和为360°,
∴∠1+∠2+∠3=360°,
故答案为:360°.
14.十
【详解】
∵n边形的内角和为
∴,.
故答案为:十边形.
15.180°
【详解】
解:∵n边形的内角和为
∴边数为8时,它的内角和为6×180°=1080°,边数为9时,它的内角和为7×180°=1260°
∴增加的度数为:1260°-1080°=180°
16.120°
【详解】
解:设这个正多边形为n边形,
根据题意得(n?2)×180°=360°+360°,
解得n=6,
所以正六边形每个内角的度数为120°,
17.
【详解】
解:,
.
沿MN翻折得到,
,.
在中,
.
18.
【详解】
四边形有2条( )对角线,五边形有5条()对角线,六边形有9条()对角线,故n边形有条对角线.
故答案:.
19.15.
【详解】
解:设这个多边形的边数为,依题意得:
,
解得,
这个多边形的边数为15.
20.15
【详解】
解:设这个多边形的边数为n,
由题意得(n-2)×180=156×n,
解得n=15,
即这个多边形的边数为15.
21.5;.
【详解】
解:设多边形的一个外角为x度,则一个内角为(x+36)度,依题意得
x+x+36=180,
解得x=72.
边数=360°÷72°=5.
内角和=(5-2)×180°=540°.
故这个多边形的边数为5,内角和是540°.
22.(1)140°;(2)∠1+∠2=90°+α.(3)如图1,∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠1?∠2=∠α?90°.
【详解】
(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°;
(2)由(1)得出:∠α+∠C=∠1+∠2,∴∠1+∠2=90°+α.
(3)如图,
分三种情况:连接ED交BA的延长线于P点,如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,∴∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠2=∠1?∠α+∠C,∴∠1?∠2=∠α?90°.
23.(1),证明见解析;(2);(3),证明见解析
【详解】
(1).证明过程如下:
如图1,∵
∴
又∵、分别是、的角平分线
∴
∵
∴
∴;
(2).证明过程如下:
如图2,连接AC
由(1)知,
是的角平分线
同理可得:
即
又,即
,即
;
(3).证明过程如下:
如图3,设与相交于点
由(1)知,
∵
∴
∵、分别是和的角平分线
∴,
∴
∵
∴
∴.
_21?????????è?????(www.21cnjy.com)_
人教版2021年八年级上册数学同步练习卷
11.3多边形及其内角和
11.3.2 多边形内角和
一、单选题
1.六边形的内角和为( )
A.360° B.540° C.720° D.180°
2.若一个正多边形的一个外角是45°,则这个正多边形的边数是( )
A.6 B.8 C.10 D.12
3.某校初一数学兴趣小组对教材《多边形的内角和与外角和》的内容进行热烈的讨论,甲说:“多边形的边数每增加1,则内角和增加180°”;乙说:“多边形的边数每增加1,则外角和增加180°”;丙说:“多边形的内角和不小于其外角和”;丁说:“只要是多边形,外角和都是360°”.你认为正确的是( )
A.甲和丁 B.乙和丙 C.丙和丁 D.以上都不对
4.下列说法正确的是( )
A.等腰三角形两边长为4,9,则三角形的周长为17或22
B.三角形的外角和为
C.在三角形,四边形,五边形中,只有三角形具有稳定性
D.四边形共有4条对角线
5.所有内角都相等的18边形,它的每个内角、外角的度数是( )
A.120°,60° B.140°,40° C.160°,20° D.100°,80°
6.设一个凸多边形,除去一个内角以外,其他内角的和为2570°,则该内角为( ).
A.40° B.90° C.120° D.130°
7.将正三角形、正四边形、正五边形按如图所示的位置摆放,如果,那么( )
A. B. C. D.
8.如图,正五边形ABCDE,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G=( )
A.36°
B.54°
C.60°
D.72°
9.如图,在中,,,,,连接BC,CD,则的度数是( )
A.45° B.50° C.55° D.80°
10.马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于,则该多边形的边数是( )
A.7 B.8 C.7或8 D.无法确定
11.如图,一束平行太阳光线FA、GB照射到正五边形ABCDE上,∠ABG=46°,则∠FAE的度数是( )
A.26°. B.44°. C.46°. D.72°
12.如图,小明从点出发,前进到点处后向右转20°,再前进到点处后又向右转20°,…,这样一直走下去,他第一次回到出发点时,一共走了( )
A. B. C. D.
二、填空题
13.如图,设、、是的外角,则____________.
14.一个多边形的内角和是 1440°,则这个多边形是__________边形.
15.如果一个多边形的边数由8变成9,其内角和增加了____________.
16.若一个正多边形的内角和比四边形的内角和多360°,则这个正多边形的每个内角的度数为___.
17.如图,在四边形ABCD中,.将沿MN翻折得到,若,则_____________.
18.四边形有2条对角线,五边形有5条对角线,六边形有9条对角线,……n边形有________条对角线.
三、解答题
19.如果一个多边形的内角和与外角和之比是 13:2,求这个多边形的边数.
已知正多边形的每个内角都是156°,求这个多边形的边数.
如果一个多边形的每一个外角都相等,且比内角小,求这个多边形的边数和内角和.
22.中,,点分别是边上的点,点是一动点,令,,.
(1)若点在线段上,如图①所示,且,则_____;
(2)若点在边上运动,如图②所示,则、、之间的关系为______;
(3)如图③,若点在斜边的延长线上运动,请写出、、之间的关系式,并说明理由.
23.在四边形中,,
(1)如图(a)所示,、分别是和的角平分线,判断与的位置关系,并证明.
(2)如图(b)所示,、分别是和的角平分线,直接写出与的位置关系.
(3)如图(c)所示,、分别是和的角平分线,判断与的位置关系,并证明.
参考答案
1.C
【详解】
解:根据多边形的内角和可得:
六边形的内角和为(6﹣2)×180°=720°.
故选C.
2.B
【详解】
∵多边形外角和=360°,
∴这个正多边形的边数是360°÷45°=8.
故选:B.
3.A
【详解】
多边形的内角和公式为,n为多边形的边数
当n增加1,则内角和增加,甲说法正确
任意多边形的外角和都等于,则乙说法错误,丁说法正确
当时,多边形的内角和为,外角和为,则丙说法错误
综上,说法正确的是甲和丁
4.C
【详解】
A.等腰三角形两边长为4,9,当4为腰长时,,不满足三角形三边关系定理,三角形的周长为,错误;
B.三角形的外角和为,错误;
C.在三角形,四边形,五边形中,只有三角形具有稳定性,正确;
D.四边形共有2条对角线,错误.
5.C
【详解】
解:∵内角都相等,
∴每个外角也都相等,
∴每个外角为:,
则每个内角为:180°-20°=160°,
故答案为:C.
6.D
【详解】
解:∵2570°÷180°=14…50°,
∴该内角应是180°-50°=130°.
故选:D.
7.C
【详解】
解:如图所示,正三角形、正四边形、正五边形的每个内角的度数分别为,
∴中间阴影部分的三角形的三个外角的度数分别为,
∵三角形的外角和为,
∴.
,
8.B
【详解】
∵正五边形外角和为360°,∴外角,
∴内角,
∵BG平分∠ABC,DG平分正五边形的外角∠EDF
∴,
在四边形BCDG中,
∴
9.B
【详解】
解:连接AC并延长交EF于点M.
,
,
,
,
,
,
,
10.C
【详解】
设少加的2个内角和为x度,边数为n.
则(n-2)×180=830+x,
即(n-2)×180=4×180+110+x,
因此x=70,n=7或x=250,n=8.
故该多边形的边数是7或8.
11.A
【详解】
解:∵图中是正五边形.
∴∠EAB=108°.
∵太阳光线互相平行,∠ABG=46°,
∴∠FAE=180°﹣∠ABG﹣∠EAB=180°﹣46°﹣108°=26°.
12.C
【详解】
∵多边形的外角和等于360°,
∴ =18,
18×5m=90m,
13.360°
【详解】
解:∵三角形的外角和为360°,
∴∠1+∠2+∠3=360°,
故答案为:360°.
14.十
【详解】
∵n边形的内角和为
∴,.
故答案为:十边形.
15.180°
【详解】
解:∵n边形的内角和为
∴边数为8时,它的内角和为6×180°=1080°,边数为9时,它的内角和为7×180°=1260°
∴增加的度数为:1260°-1080°=180°
16.120°
【详解】
解:设这个正多边形为n边形,
根据题意得(n?2)×180°=360°+360°,
解得n=6,
所以正六边形每个内角的度数为120°,
17.
【详解】
解:,
.
沿MN翻折得到,
,.
在中,
.
18.
【详解】
四边形有2条( )对角线,五边形有5条()对角线,六边形有9条()对角线,故n边形有条对角线.
故答案:.
19.15.
【详解】
解:设这个多边形的边数为,依题意得:
,
解得,
这个多边形的边数为15.
20.15
【详解】
解:设这个多边形的边数为n,
由题意得(n-2)×180=156×n,
解得n=15,
即这个多边形的边数为15.
21.5;.
【详解】
解:设多边形的一个外角为x度,则一个内角为(x+36)度,依题意得
x+x+36=180,
解得x=72.
边数=360°÷72°=5.
内角和=(5-2)×180°=540°.
故这个多边形的边数为5,内角和是540°.
22.(1)140°;(2)∠1+∠2=90°+α.(3)如图1,∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠1?∠2=∠α?90°.
【详解】
(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°;
(2)由(1)得出:∠α+∠C=∠1+∠2,∴∠1+∠2=90°+α.
(3)如图,
分三种情况:连接ED交BA的延长线于P点,如图1,由三角形的外角性质,∠2=∠C+∠1+∠α,∴∠2?∠1=90°+∠α;如图2,∠α=0°,∠2=∠1+90°;如图3,∠2=∠1?∠α+∠C,∴∠1?∠2=∠α?90°.
23.(1),证明见解析;(2);(3),证明见解析
【详解】
(1).证明过程如下:
如图1,∵
∴
又∵、分别是、的角平分线
∴
∵
∴
∴;
(2).证明过程如下:
如图2,连接AC
由(1)知,
是的角平分线
同理可得:
即
又,即
,即
;
(3).证明过程如下:
如图3,设与相交于点
由(1)知,
∵
∴
∵、分别是和的角平分线
∴,
∴
∵
∴
∴.
_21?????????è?????(www.21cnjy.com)_
