12.3 角的平分线的性质 课时达标检测(含解析)
文档属性
| 名称 | 12.3 角的平分线的性质 课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 15:54:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2021年八年级上册数学同步练习卷
12.3角的平分线的性质
一、单选题
1.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
A.1 B.2 C. D.4
2.如图,OA平分∠BAC,OM⊥AC于点M,ON⊥AB于点N,若ON=8cm,则OM长为( )
A.4cm B.5cm C.8cm D.20cm
3.如图,OP平分∠AOB,PA⊥OA于点A,PB⊥OB于点B.下列结论中,不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
4.如图,点到、、的距离恰好相等,则点的位置:①在的平分线上;②在的平分线上;③在的平分线上;④恰好是、、三条平分线的交点.上述结论中,正确的个数有( )
A.个 B.个 C.个 D.个
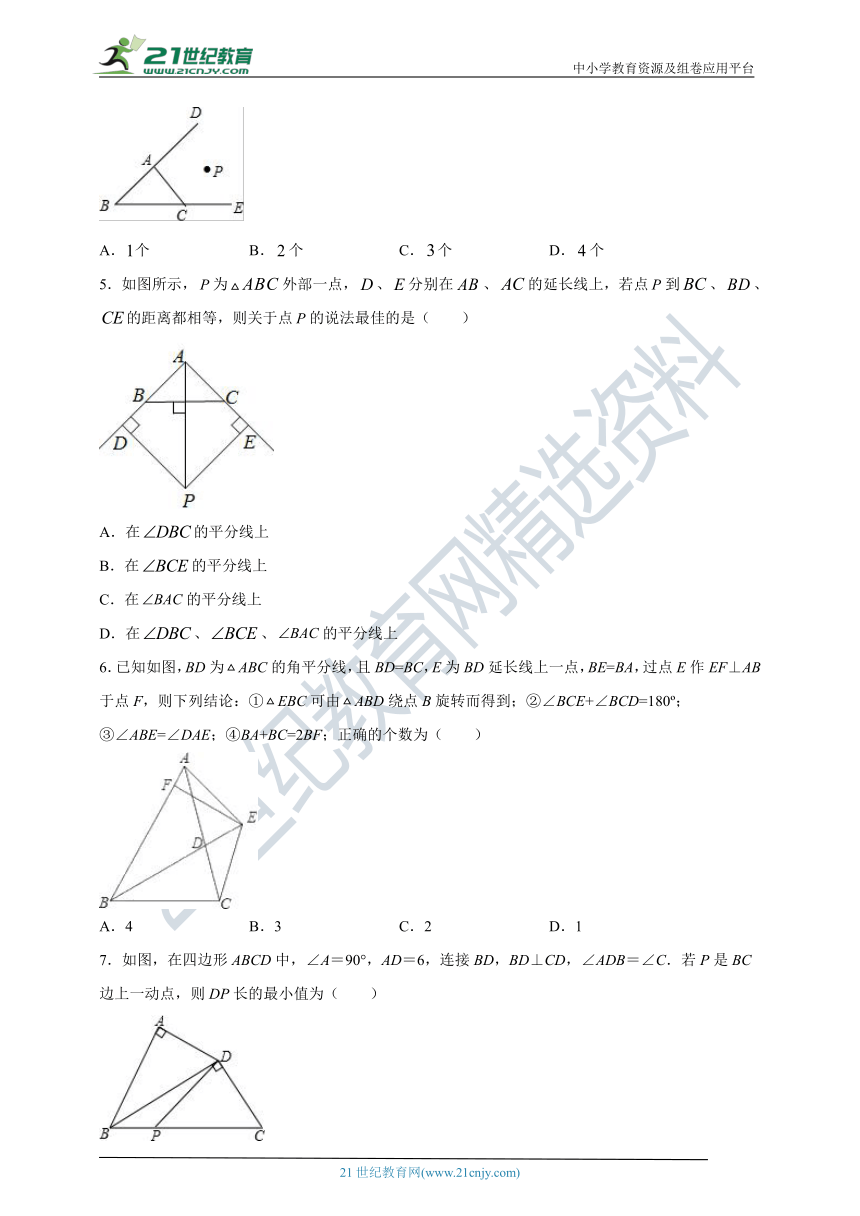
5.如图所示,为外部一点,、分别在、的延长线上,若点到、、的距离都相等,则关于点的说法最佳的是( )
A.在的平分线上
B.在的平分线上
C.在的平分线上
D.在、、的平分线上
6.已知如图,BD为ABC的角平分线,且BD=BC,E为BD延长线上一点,BE=BA,过点E作EF⊥AB于点F,则下列结论:①EBC可由ABD绕点B旋转而得到;②∠BCE+∠BCD=180?;③∠ABE=∠DAE;④BA+BC=2BF;正确的个数为( )
A.4 B.3 C.2 D.1
7.如图,在四边形ABCD中,∠A=90°,AD=6,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.4 B.6 C.3 D.12
8.如图,在中,点D是BC边上一点,已知,,CE平分交AB于点E,连接DE,则的度数为( )
A. B. C. D.
9.△ABC中,∠C=90°,AC=8,BC=6,角平分线AD、BE相交于点O,则四边形OECD的面积为( )
A.5 B. C. D.8
10.如图,在△ABC中,AD⊥BC,CE平分∠ACB,AD交CE于点F,已知△AFC的面积为5,FD=2,则AC长是( )
A.2.5 B.4 C.5 D.6
11.如图,中,,、的平分线交于,是延长线上一点,且.下列结论:①;②;③.其中所有正确结论的序号有( ).
A.①② B.①③ C.②③ D.①②③
12.如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是( )
A.PD=DQ B.DE=AC C.AE=CQ D.PQ⊥AB
二、填空题
13.在三角形中,到三边距离相等的点是____________.
14.角的内部到角两边距离相等的点在_______上.
15.如图,在△ABC中,∠C=90°,AP平分∠CAB,且PC=3,PB=5,则点P到边AB的距离是 ______________
16.我们定义:一个三角形最小内角的角平分线将这个三角形分割得到的两个三角形它们的面积之比称为“最小角割比Ω”(),那么三边长分别为7,24,25的三角形的最小角割比Ω是______.
17.如图,任意画一个∠A=60°的,再分别作的两条角平分线BE和CD,BE和CD交于点P,连接AP.有以下结论:①∠BPC=120°;②AP平分∠BAC;③PD=PE;④BD+CE=BC;⑤.其中正确结论的序号是___.
18.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列结论:①EF=BE+CF;②点O到△ABC各边的距离相等;③∠BOC=90°+∠A;④设OD=m,AE+AF=n,则S△AEF=mn.⑤AD=(AB+AC﹣BC).其中正确的结论是__.
三、解答题
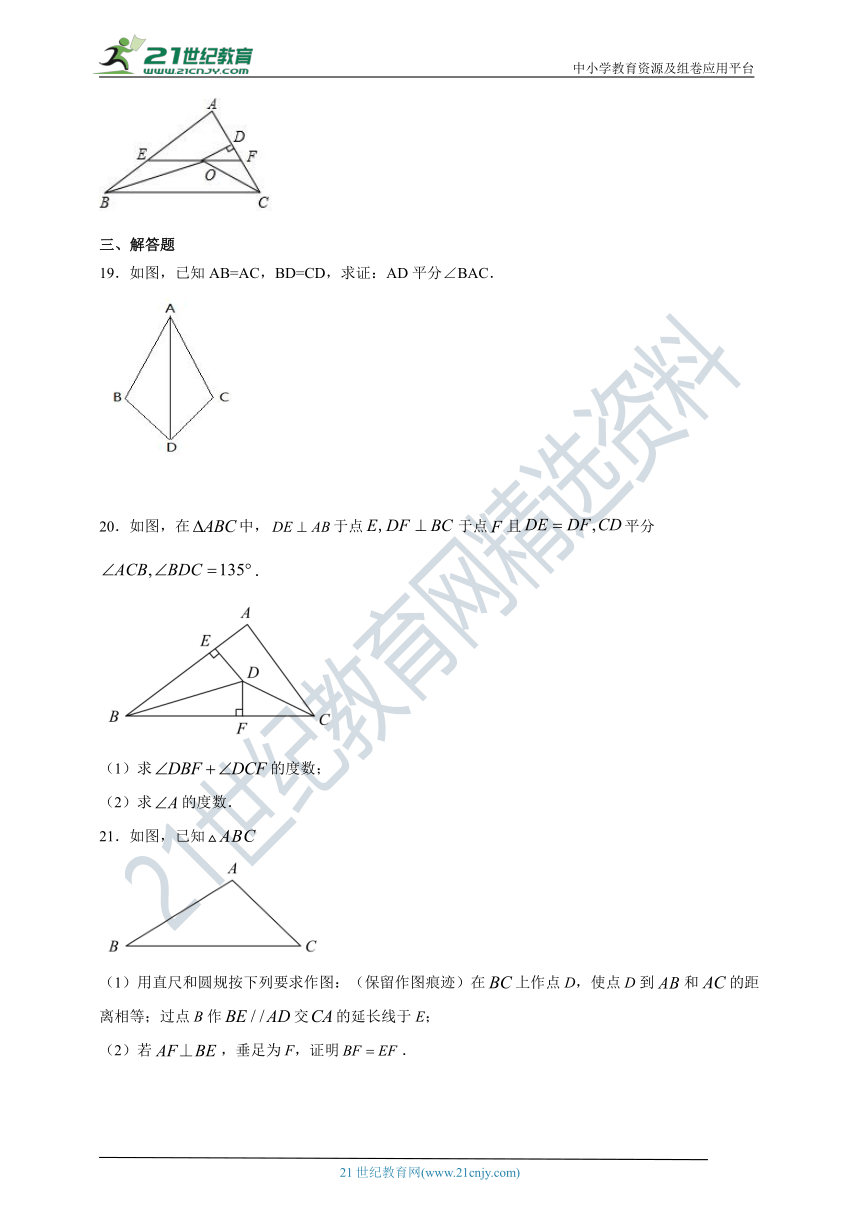
19.如图,已知AB=AC,BD=CD,求证:AD平分∠BAC.
20.如图,在中,于点于点且平分.
(1)求的度数;
(2)求的度数.
21.如图,已知
(1)用直尺和圆规按下列要求作图:(保留作图痕迹)在上作点D,使点D到和的距离相等;过点B作交的延长线于E;
(2)若,垂足为F,证明.
22.如图,中,于点,,点在上,,连接.
(1)求证:;
(2)延长交于点,连接,求的度数;
(3)过点作,,连接交于点,若,,直接写出的面积.
23.如图,在中,已知,动点同时从两点出 发,分别沿方向匀速移动,动点的速度是,动点的速度是,当点到达点时,两点停止运动,连接,设点的运动时间为,试解答下面的问题:
当时,求的面积?
当为何值时,点在线段的垂直平分线上?
是否存在某一时刻,使点在的角平分线上,若存在,请求出的值;若不存 在,请说明理由?
请用含有的代数式表示四边形的面积.
参考答案
1.B
【详解】
如图,过点P作,垂足为点G,根据角平分线上的点到角的两边距离相等可得,.
2.C
【详解】
解:∵OA是∠BAC的平分线,OM⊥AC,ON⊥AB,
∴OM=ON=8cm,
3.D
【详解】
解:∵OP平分∠AOB,PA⊥OA于点A,PB⊥OB于点B,
∴PA=PB,故A成立,不符合题意;
∵OP=OP,
∴Rt△PAO≌Rt△PBO(HL),
∴∠APO=∠BPO,OA=OB,故C选项成立,不符合题意;
∴PO平分∠APB,故B选项成立,不符合题意;
由题目已知条件可知AB垂直平分OP不一定成立,故D选项符合题意;
4.D
【详解】
∵点P到BE,BD的距离相等,∴点P在∠B的平分线上,故①正确;
∵点P到BD、AC的距离相等,∴点P在∠DAC的平分线上,故②正确;
∵点P到BE、AC的距离相等,∴点P在∠ECA的平分线上,故③正确;
∵点P到BE、BD、AC的距离都相等,∴恰好是∠B、∠DAC、∠ECA三条平分线的交点,故④正确;
综上可得①②③④都正确.
5.D
【详解】
由于点P到BC、BD的距离相等,则点P在∠DBC的平分线上,
点P到BD、CE的距离相等,则点P在∠BAC的平分线上,
点P到BC、CE的距离相等,则点P在∠BCE的平分线上,
6.A
【详解】
∵BD为ABC的角平分线,
∴∠ABD=∠EBC,
在△ABD和△EBC中,,
∴△ABD≌△EBC,
∴EBC可由ABD绕点B旋转而得到,故①正确,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∵BC=BD,
∴∠BCD=∠BDC,
∴∠BCE+∠BCD=∠BDA+∠BDC=180?;故②正确,
∵AB=BE,BD=BC,
∴∠BCD==90°-∠EBC,∠AED==90°-∠ABD,
∵∠ABD=∠EBC,
∴∠BCD=∠AED,
∵∠ADE=∠BDC,
∴∠ABE=∠DAE,故③正确,
作EG⊥BC,交BC延长线于点G,
∵BD为∠ABC的角平分线,EF⊥AB,
∴EF=EG,
在Rt△BEF和Rt△BEG中,,
∴Rt△BEF≌Rt△BEG,
∴,
∵△ABD≌△EBC,
∴AD=CE,
∵∠ADE=∠BDC=∠BCD=∠AED,
∴AD=AE,
∴AE=CE,
在Rt△AEF和Rt△CEG中,,
∴Rt△AEF≌Rt△CEG,
∴AF=CG,
∴AB+BC=BF+AF+BG-CG=2BF,故④正确,
综上所述,正确的结论为①②③④,
7.B
【详解】
解:∵BD⊥CD,
∴∠BDC=90°,
∴∠C+∠CBD=90°,
∵∠A=90°
∴∠ABD+∠ADB=90°,
∵∠ADB=∠C,
∴∠ABD=∠CBD,
当DP⊥BC时,DP的长度最小,
∵AD⊥AB,
∴DP=AD,
∵AD=6,
∴DP的最小值是6,
8.B
【详解】
解:过点E作于M,于N,于H,如图,
,,
,
平分,
,
平分,
,
,
平分,
,
由三角形外角可得:,
,
,
而,
,
9.C
【详解】
解:如图,作OM⊥AB于M,OJ⊥BC于J,OK⊥AC于K,DH⊥BC于H,连接OC.
在Rt△ABC中,
∵∠ACB=90°,AC=8,BC=6,
∴AB=10,
∵点O是△ABC的内心,
∴OM=OJ=OK2,
∵∠DCA=∠DHA=90°,AD=AD(公共边),∠DAC=∠DAH,
∴△DAC≌△DAH(AAS),
∴CD=DH,AC=AH=8,
∴BH=10﹣8=2,
设CD=DH=x,
在Rt△BDH中,
∵BD2=BH2+DH2,
∴(6﹣x)2=x2+22,
∴x,
同法可求:EC=3,
∴S四边形CDOE=S△COD+S△COE?CD?OJ?EC?OK23×2.
故选:C.
10.C
【详解】
解:过F作FH⊥AC,
∵AD⊥BC,CE平分∠ACB,
∴FH=DF,
∵FD=2,
∴FH=2,
∵△AFC的面积为5,
∴AC?FH=×2×AC=5,
∴AC=5,
故选:C.
11.D
【解析】
分析:根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠EBC+∠ECB,然后求出∠BEC=120°,判断①正确;过点D作DF⊥AB于F,DG⊥AC的延长线于G,根据角平分线上的点到角的两边的距离相等可得DF=DG,再求出∠BDF=∠CDG,然后利用“角边角”证明△BDF和△CDG全等,根据全等三角形对应边相等可得BD=CD,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB,根据等角对等边可得BD=DE,判断②正确,再求出B,C,E三点在以D为圆心,以BD为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE,判断③正确.
详解:∵,
∴,
∵、分别为、的平分线,
∴,,
∴,
∴,
故①正确.
如图,过点作于,的延长线于,
∵、分别为、的平分线,
∴为的平分线,
∴,
∴,
又∵,
∴,.
∴,
∵在和中,
,
∴≌,
∴,
∴,
∴,
∵平分,平分,
∴,,
根据三角形的外角性质,
,
∴,
∴,故②正确.
∵,
∴、、三点在以为圆心,以为半径的圆上,
∴,故③正确,
综上所述,正确结论有①②③,
12.D
【详解】
过P作PF∥CQ交AC于F,∴∠FPD=∠Q,∵△ABC是等边三角形,
∴∠A=∠ACB=60°,∴∠A=∠AFP=60°,∴AP=PF,∵PA=CQ,∴PF=CQ,在△PFD与△DCQ中,,∴△PFD≌△QCD,∴PD=DQ,DF=CD,∴A选项正确,∵AE=EF,∴DE=AC,∴B选项正确,∵PE⊥AC,∠A=60°,∴AE=AP=CQ,∴C选项正确,故选D.
13.三条角平分线的交点
【详解】
解:∵OG⊥AB,OF⊥AC,OG=OF,
∴O在∠A的平分线上,
同理O在∠B的平分线上,
O在∠C的平分线上,
即O是三条角平分线的交点,
故答案为:三条角平分线的交点.
14.角的平分线
【详解】
∵角平分线性质的逆定理:角的内部到角两边距离相等的点在角的平分线上
∴答案为角的平分线
故答案为角的平分线.
15.3
【详解】
解:作PH⊥AB于H,如图,
∵AP平分∠CAB,且∠C=90°,
∴,即点P到边AB的距离是3.
故答案为3.
16..
【详解】
解:如图示,,,,
则,根据题意,作的角平分线交于点,
过点,作交于点,
过点,作交于点,
则
∵,,
则()
故答案是:.
17.①②③④⑤
【详解】
∵BE,CD分别是∠ABC和∠ACB的平分线,∠A=60°,
∴∠PBC+∠PCB=,
∴∠BPC=180°-(∠PBC+∠PCB)=180°-60°=120°,
故①正确;
∵∠BPC=120°,
∴∠DPE=120°,
过点P作PF⊥AB,PG⊥AC,PH⊥BC,
∵BE,CD分别是∠ABC和∠ACB的平分线,
∴PF=PH=PG,
∴AP平分∠BAC,
故②正确;
由②可知:PF=PH=PG,
∵∠BAC=60°,∠AFP=∠AGP=90°,
∴∠FPG=120°,
∴∠DPF=∠EPG,
∴?PFD??PGE(ASA),
∴PD=PE,
∴③正确;
又∵BP=BP,PF=PH,
∴Rt?BHP?Rt?BFP(HL),
同理:Rt?CHP?Rt?CGP,
∴BH=BD+DF,CH=CE-GE,
两式相加得:BH+ CH =BD+DF+CE-GE,
∵DF=GE,
∴BD+CE=BC,
∴④正确;
∵?PBD,?PCE,?PBC,的高相等,BD+CE=BC,
∴,
故⑤正确.
故答案是:①②③④⑤
18.①②③⑤
【详解】
解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故③正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE?OM+AF?OD=OD?(AE+AF)=mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故②正确.
可证△AMO≌△ADO,△BMO≌BNO,△CDO≌△CNO
∴AM=AD,BM=BN,CD=CN,
∵AM+BM=AB,AD+CD=AC,BN+CN=BC,
∴AD=(AB+AC﹣BC)故⑤正确,
故答案为:①②③⑤.
.
19.见解析
【分析】
利用SSS判定△ABD≌△ACD,再根据全等三角形的对应角相等得到:∠BAD=∠CAD,则AD是∠BAC的平分线.
【详解】
在△ADB和△ADC中,
,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
20.(1)45°;(2)90°
【详解】
解:(1)∵∠BDC=135°,
∴∠DBF+∠DCF=180°-135°=45°;
(2)∵DE⊥AB,DF⊥BC,DE=DF,
∴BD平分∠ABC,即∠ABD=∠CBD,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠A=180°-∠ABC-∠ACB=180°-2(∠DBC+∠DCB)=180°-2×45°=90°.
21.(1)见解析;(2)见解析
【分析】
(1)作∠BAC的平分线,交BC于D,作∠ABE=∠BAD,交CA延长线于E即可;
(2)根据已知条件,利用ASA证明△AFE≌△AFB,可得结果.
【详解】
解:(1)如图所示,AD和BE即为所作;
(2)∵BE∥AD,AF⊥BE,
∴∠DAF=180°-90°=90°,∠EAF+∠CAD=90°,
即∠BAF+∠BAD=90°,
由(1)可知:∠BAD=∠CAD,
∴∠CAD+∠BAF=90°,
∴∠BAF=∠EAF,
∵∠AFE=∠AFB=90°,AF=AF,
∴△AFE≌△AFB(ASA),
∴EF=BF.
22.(1)见解析;(2)∠CFD=135°;(3)△NBC的面积为21.
【分析】
(1)由“SAS”可证△BDE≌△CDA,可得BE=CA;
(2)过点D作DG⊥AC于G,DH⊥BF于H,由全等三角形的性质可得∠DBE=∠ACD,S△BDE=S△ADC,由面积关系可求DH=DG,由角平分线的性质可得∠DFG=∠DFH=45°,即可求解;
(3)在CD上截取DE=AD=5,连接BE,延长BE交AC于F,由△BEN≌△MCN,可得EN=CN,由三角形的面积公式可求解.
【详解】
证明(1)在△BDE和△CDA中,
,
∴△BDE≌△CDA(SAS),
∴BE=CA;
(2)如图2,过点D作DG⊥AC于G,DH⊥BF于H,
∵△BDE≌△CDA,
∴∠DBE=∠DCA,S△BDE=S△ADC,
∵∠DBE+∠A=∠ACD+∠A=90°,
∴∠AFB=∠CFB=90°,
∵S△BDE=S△ADC,
∴,
∴DH=DG,
又∵DG⊥AC,DH⊥BF,
∴∠DFG=∠DFH=45°,
∴∠CFD=135°;
(3)如图3,在CD上截取DE=AD=5,连接BE,延长BE交AC于F,
由(1)、(2)可得BE=AC,BF⊥AC,BD=CD=12,
∵CM⊥CA,
∴BF∥CM,
∴∠M=∠FBN,
∵CM=CA,
∴CM=BE,
在△BEN和△MCN中,
,
∴△BEN≌△MCN(AAS),
∴EN=CN,
∵EC=CD-DE=12-5=7,
∴,
∴△NBC的面积,
故△NBC的面积为21.
23.(1);(2)t=4;(3)不存在,理由见详解;(4).
【详解】
解:(1)∵在中,已知,
∴AB=12cm,BC= cm,
当t=1时,AP=2cm,
∴,,
过P作PM垂直于BC,
则有,
∴.
(2)B在PQ的垂直平分线上即BP=BQ,
设t=m,如下图,
则有BP=12-2m, BQ=m,得出12-2m=m,解得m=4,
∴t=4时,点在线段的垂直平分线上.
(3)Q在的平分线上,如图,
∵
∴,
∴,
设CQ为n,AQ为2n,则有,解得n=或-(舍去),
∴
∴当时,Q在的平分线上,此时,
∵
∴不存在某一时刻,使点在的角平分线上.
(4)连接AQ,如下图,
,
过P作PD垂直于BC,如上图,
则有,
∴
.
_21?????????è?????(www.21cnjy.com)_
人教版2021年八年级上册数学同步练习卷
12.3角的平分线的性质
一、单选题
1.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
A.1 B.2 C. D.4
2.如图,OA平分∠BAC,OM⊥AC于点M,ON⊥AB于点N,若ON=8cm,则OM长为( )
A.4cm B.5cm C.8cm D.20cm
3.如图,OP平分∠AOB,PA⊥OA于点A,PB⊥OB于点B.下列结论中,不一定成立的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
4.如图,点到、、的距离恰好相等,则点的位置:①在的平分线上;②在的平分线上;③在的平分线上;④恰好是、、三条平分线的交点.上述结论中,正确的个数有( )
A.个 B.个 C.个 D.个
5.如图所示,为外部一点,、分别在、的延长线上,若点到、、的距离都相等,则关于点的说法最佳的是( )
A.在的平分线上
B.在的平分线上
C.在的平分线上
D.在、、的平分线上
6.已知如图,BD为ABC的角平分线,且BD=BC,E为BD延长线上一点,BE=BA,过点E作EF⊥AB于点F,则下列结论:①EBC可由ABD绕点B旋转而得到;②∠BCE+∠BCD=180?;③∠ABE=∠DAE;④BA+BC=2BF;正确的个数为( )
A.4 B.3 C.2 D.1
7.如图,在四边形ABCD中,∠A=90°,AD=6,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )
A.4 B.6 C.3 D.12
8.如图,在中,点D是BC边上一点,已知,,CE平分交AB于点E,连接DE,则的度数为( )
A. B. C. D.
9.△ABC中,∠C=90°,AC=8,BC=6,角平分线AD、BE相交于点O,则四边形OECD的面积为( )
A.5 B. C. D.8
10.如图,在△ABC中,AD⊥BC,CE平分∠ACB,AD交CE于点F,已知△AFC的面积为5,FD=2,则AC长是( )
A.2.5 B.4 C.5 D.6
11.如图,中,,、的平分线交于,是延长线上一点,且.下列结论:①;②;③.其中所有正确结论的序号有( ).
A.①② B.①③ C.②③ D.①②③
12.如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论中不一定正确的是( )
A.PD=DQ B.DE=AC C.AE=CQ D.PQ⊥AB
二、填空题
13.在三角形中,到三边距离相等的点是____________.
14.角的内部到角两边距离相等的点在_______上.
15.如图,在△ABC中,∠C=90°,AP平分∠CAB,且PC=3,PB=5,则点P到边AB的距离是 ______________
16.我们定义:一个三角形最小内角的角平分线将这个三角形分割得到的两个三角形它们的面积之比称为“最小角割比Ω”(),那么三边长分别为7,24,25的三角形的最小角割比Ω是______.
17.如图,任意画一个∠A=60°的,再分别作的两条角平分线BE和CD,BE和CD交于点P,连接AP.有以下结论:①∠BPC=120°;②AP平分∠BAC;③PD=PE;④BD+CE=BC;⑤.其中正确结论的序号是___.
18.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列结论:①EF=BE+CF;②点O到△ABC各边的距离相等;③∠BOC=90°+∠A;④设OD=m,AE+AF=n,则S△AEF=mn.⑤AD=(AB+AC﹣BC).其中正确的结论是__.
三、解答题
19.如图,已知AB=AC,BD=CD,求证:AD平分∠BAC.
20.如图,在中,于点于点且平分.
(1)求的度数;
(2)求的度数.
21.如图,已知
(1)用直尺和圆规按下列要求作图:(保留作图痕迹)在上作点D,使点D到和的距离相等;过点B作交的延长线于E;
(2)若,垂足为F,证明.
22.如图,中,于点,,点在上,,连接.
(1)求证:;
(2)延长交于点,连接,求的度数;
(3)过点作,,连接交于点,若,,直接写出的面积.
23.如图,在中,已知,动点同时从两点出 发,分别沿方向匀速移动,动点的速度是,动点的速度是,当点到达点时,两点停止运动,连接,设点的运动时间为,试解答下面的问题:
当时,求的面积?
当为何值时,点在线段的垂直平分线上?
是否存在某一时刻,使点在的角平分线上,若存在,请求出的值;若不存 在,请说明理由?
请用含有的代数式表示四边形的面积.
参考答案
1.B
【详解】
如图,过点P作,垂足为点G,根据角平分线上的点到角的两边距离相等可得,.
2.C
【详解】
解:∵OA是∠BAC的平分线,OM⊥AC,ON⊥AB,
∴OM=ON=8cm,
3.D
【详解】
解:∵OP平分∠AOB,PA⊥OA于点A,PB⊥OB于点B,
∴PA=PB,故A成立,不符合题意;
∵OP=OP,
∴Rt△PAO≌Rt△PBO(HL),
∴∠APO=∠BPO,OA=OB,故C选项成立,不符合题意;
∴PO平分∠APB,故B选项成立,不符合题意;
由题目已知条件可知AB垂直平分OP不一定成立,故D选项符合题意;
4.D
【详解】
∵点P到BE,BD的距离相等,∴点P在∠B的平分线上,故①正确;
∵点P到BD、AC的距离相等,∴点P在∠DAC的平分线上,故②正确;
∵点P到BE、AC的距离相等,∴点P在∠ECA的平分线上,故③正确;
∵点P到BE、BD、AC的距离都相等,∴恰好是∠B、∠DAC、∠ECA三条平分线的交点,故④正确;
综上可得①②③④都正确.
5.D
【详解】
由于点P到BC、BD的距离相等,则点P在∠DBC的平分线上,
点P到BD、CE的距离相等,则点P在∠BAC的平分线上,
点P到BC、CE的距离相等,则点P在∠BCE的平分线上,
6.A
【详解】
∵BD为ABC的角平分线,
∴∠ABD=∠EBC,
在△ABD和△EBC中,,
∴△ABD≌△EBC,
∴EBC可由ABD绕点B旋转而得到,故①正确,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∵BC=BD,
∴∠BCD=∠BDC,
∴∠BCE+∠BCD=∠BDA+∠BDC=180?;故②正确,
∵AB=BE,BD=BC,
∴∠BCD==90°-∠EBC,∠AED==90°-∠ABD,
∵∠ABD=∠EBC,
∴∠BCD=∠AED,
∵∠ADE=∠BDC,
∴∠ABE=∠DAE,故③正确,
作EG⊥BC,交BC延长线于点G,
∵BD为∠ABC的角平分线,EF⊥AB,
∴EF=EG,
在Rt△BEF和Rt△BEG中,,
∴Rt△BEF≌Rt△BEG,
∴,
∵△ABD≌△EBC,
∴AD=CE,
∵∠ADE=∠BDC=∠BCD=∠AED,
∴AD=AE,
∴AE=CE,
在Rt△AEF和Rt△CEG中,,
∴Rt△AEF≌Rt△CEG,
∴AF=CG,
∴AB+BC=BF+AF+BG-CG=2BF,故④正确,
综上所述,正确的结论为①②③④,
7.B
【详解】
解:∵BD⊥CD,
∴∠BDC=90°,
∴∠C+∠CBD=90°,
∵∠A=90°
∴∠ABD+∠ADB=90°,
∵∠ADB=∠C,
∴∠ABD=∠CBD,
当DP⊥BC时,DP的长度最小,
∵AD⊥AB,
∴DP=AD,
∵AD=6,
∴DP的最小值是6,
8.B
【详解】
解:过点E作于M,于N,于H,如图,
,,
,
平分,
,
平分,
,
,
平分,
,
由三角形外角可得:,
,
,
而,
,
9.C
【详解】
解:如图,作OM⊥AB于M,OJ⊥BC于J,OK⊥AC于K,DH⊥BC于H,连接OC.
在Rt△ABC中,
∵∠ACB=90°,AC=8,BC=6,
∴AB=10,
∵点O是△ABC的内心,
∴OM=OJ=OK2,
∵∠DCA=∠DHA=90°,AD=AD(公共边),∠DAC=∠DAH,
∴△DAC≌△DAH(AAS),
∴CD=DH,AC=AH=8,
∴BH=10﹣8=2,
设CD=DH=x,
在Rt△BDH中,
∵BD2=BH2+DH2,
∴(6﹣x)2=x2+22,
∴x,
同法可求:EC=3,
∴S四边形CDOE=S△COD+S△COE?CD?OJ?EC?OK23×2.
故选:C.
10.C
【详解】
解:过F作FH⊥AC,
∵AD⊥BC,CE平分∠ACB,
∴FH=DF,
∵FD=2,
∴FH=2,
∵△AFC的面积为5,
∴AC?FH=×2×AC=5,
∴AC=5,
故选:C.
11.D
【解析】
分析:根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠EBC+∠ECB,然后求出∠BEC=120°,判断①正确;过点D作DF⊥AB于F,DG⊥AC的延长线于G,根据角平分线上的点到角的两边的距离相等可得DF=DG,再求出∠BDF=∠CDG,然后利用“角边角”证明△BDF和△CDG全等,根据全等三角形对应边相等可得BD=CD,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB,根据等角对等边可得BD=DE,判断②正确,再求出B,C,E三点在以D为圆心,以BD为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE,判断③正确.
详解:∵,
∴,
∵、分别为、的平分线,
∴,,
∴,
∴,
故①正确.
如图,过点作于,的延长线于,
∵、分别为、的平分线,
∴为的平分线,
∴,
∴,
又∵,
∴,.
∴,
∵在和中,
,
∴≌,
∴,
∴,
∴,
∵平分,平分,
∴,,
根据三角形的外角性质,
,
∴,
∴,故②正确.
∵,
∴、、三点在以为圆心,以为半径的圆上,
∴,故③正确,
综上所述,正确结论有①②③,
12.D
【详解】
过P作PF∥CQ交AC于F,∴∠FPD=∠Q,∵△ABC是等边三角形,
∴∠A=∠ACB=60°,∴∠A=∠AFP=60°,∴AP=PF,∵PA=CQ,∴PF=CQ,在△PFD与△DCQ中,,∴△PFD≌△QCD,∴PD=DQ,DF=CD,∴A选项正确,∵AE=EF,∴DE=AC,∴B选项正确,∵PE⊥AC,∠A=60°,∴AE=AP=CQ,∴C选项正确,故选D.
13.三条角平分线的交点
【详解】
解:∵OG⊥AB,OF⊥AC,OG=OF,
∴O在∠A的平分线上,
同理O在∠B的平分线上,
O在∠C的平分线上,
即O是三条角平分线的交点,
故答案为:三条角平分线的交点.
14.角的平分线
【详解】
∵角平分线性质的逆定理:角的内部到角两边距离相等的点在角的平分线上
∴答案为角的平分线
故答案为角的平分线.
15.3
【详解】
解:作PH⊥AB于H,如图,
∵AP平分∠CAB,且∠C=90°,
∴,即点P到边AB的距离是3.
故答案为3.
16..
【详解】
解:如图示,,,,
则,根据题意,作的角平分线交于点,
过点,作交于点,
过点,作交于点,
则
∵,,
则()
故答案是:.
17.①②③④⑤
【详解】
∵BE,CD分别是∠ABC和∠ACB的平分线,∠A=60°,
∴∠PBC+∠PCB=,
∴∠BPC=180°-(∠PBC+∠PCB)=180°-60°=120°,
故①正确;
∵∠BPC=120°,
∴∠DPE=120°,
过点P作PF⊥AB,PG⊥AC,PH⊥BC,
∵BE,CD分别是∠ABC和∠ACB的平分线,
∴PF=PH=PG,
∴AP平分∠BAC,
故②正确;
由②可知:PF=PH=PG,
∵∠BAC=60°,∠AFP=∠AGP=90°,
∴∠FPG=120°,
∴∠DPF=∠EPG,
∴?PFD??PGE(ASA),
∴PD=PE,
∴③正确;
又∵BP=BP,PF=PH,
∴Rt?BHP?Rt?BFP(HL),
同理:Rt?CHP?Rt?CGP,
∴BH=BD+DF,CH=CE-GE,
两式相加得:BH+ CH =BD+DF+CE-GE,
∵DF=GE,
∴BD+CE=BC,
∴④正确;
∵?PBD,?PCE,?PBC,的高相等,BD+CE=BC,
∴,
故⑤正确.
故答案是:①②③④⑤
18.①②③⑤
【详解】
解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故③正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE?OM+AF?OD=OD?(AE+AF)=mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故②正确.
可证△AMO≌△ADO,△BMO≌BNO,△CDO≌△CNO
∴AM=AD,BM=BN,CD=CN,
∵AM+BM=AB,AD+CD=AC,BN+CN=BC,
∴AD=(AB+AC﹣BC)故⑤正确,
故答案为:①②③⑤.
.
19.见解析
【分析】
利用SSS判定△ABD≌△ACD,再根据全等三角形的对应角相等得到:∠BAD=∠CAD,则AD是∠BAC的平分线.
【详解】
在△ADB和△ADC中,
,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD,
∴AD是∠BAC的平分线.
20.(1)45°;(2)90°
【详解】
解:(1)∵∠BDC=135°,
∴∠DBF+∠DCF=180°-135°=45°;
(2)∵DE⊥AB,DF⊥BC,DE=DF,
∴BD平分∠ABC,即∠ABD=∠CBD,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠A=180°-∠ABC-∠ACB=180°-2(∠DBC+∠DCB)=180°-2×45°=90°.
21.(1)见解析;(2)见解析
【分析】
(1)作∠BAC的平分线,交BC于D,作∠ABE=∠BAD,交CA延长线于E即可;
(2)根据已知条件,利用ASA证明△AFE≌△AFB,可得结果.
【详解】
解:(1)如图所示,AD和BE即为所作;
(2)∵BE∥AD,AF⊥BE,
∴∠DAF=180°-90°=90°,∠EAF+∠CAD=90°,
即∠BAF+∠BAD=90°,
由(1)可知:∠BAD=∠CAD,
∴∠CAD+∠BAF=90°,
∴∠BAF=∠EAF,
∵∠AFE=∠AFB=90°,AF=AF,
∴△AFE≌△AFB(ASA),
∴EF=BF.
22.(1)见解析;(2)∠CFD=135°;(3)△NBC的面积为21.
【分析】
(1)由“SAS”可证△BDE≌△CDA,可得BE=CA;
(2)过点D作DG⊥AC于G,DH⊥BF于H,由全等三角形的性质可得∠DBE=∠ACD,S△BDE=S△ADC,由面积关系可求DH=DG,由角平分线的性质可得∠DFG=∠DFH=45°,即可求解;
(3)在CD上截取DE=AD=5,连接BE,延长BE交AC于F,由△BEN≌△MCN,可得EN=CN,由三角形的面积公式可求解.
【详解】
证明(1)在△BDE和△CDA中,
,
∴△BDE≌△CDA(SAS),
∴BE=CA;
(2)如图2,过点D作DG⊥AC于G,DH⊥BF于H,
∵△BDE≌△CDA,
∴∠DBE=∠DCA,S△BDE=S△ADC,
∵∠DBE+∠A=∠ACD+∠A=90°,
∴∠AFB=∠CFB=90°,
∵S△BDE=S△ADC,
∴,
∴DH=DG,
又∵DG⊥AC,DH⊥BF,
∴∠DFG=∠DFH=45°,
∴∠CFD=135°;
(3)如图3,在CD上截取DE=AD=5,连接BE,延长BE交AC于F,
由(1)、(2)可得BE=AC,BF⊥AC,BD=CD=12,
∵CM⊥CA,
∴BF∥CM,
∴∠M=∠FBN,
∵CM=CA,
∴CM=BE,
在△BEN和△MCN中,
,
∴△BEN≌△MCN(AAS),
∴EN=CN,
∵EC=CD-DE=12-5=7,
∴,
∴△NBC的面积,
故△NBC的面积为21.
23.(1);(2)t=4;(3)不存在,理由见详解;(4).
【详解】
解:(1)∵在中,已知,
∴AB=12cm,BC= cm,
当t=1时,AP=2cm,
∴,,
过P作PM垂直于BC,
则有,
∴.
(2)B在PQ的垂直平分线上即BP=BQ,
设t=m,如下图,
则有BP=12-2m, BQ=m,得出12-2m=m,解得m=4,
∴t=4时,点在线段的垂直平分线上.
(3)Q在的平分线上,如图,
∵
∴,
∴,
设CQ为n,AQ为2n,则有,解得n=或-(舍去),
∴
∴当时,Q在的平分线上,此时,
∵
∴不存在某一时刻,使点在的角平分线上.
(4)连接AQ,如下图,
,
过P作PD垂直于BC,如上图,
则有,
∴
.
_21?????????è?????(www.21cnjy.com)_
