12.2 三角形全等的判断 课时达标检测(含解析)
文档属性
| 名称 | 12.2 三角形全等的判断 课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 15:54:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021年八年级上册数学同步练习卷
12.2三角形全等的判断
一、单选题
1.不能使两个直角三角形全等的条件是( ).
A.一条直角边及其对角对应相等 B.斜边和两条直角边对应相等
C.斜边和一条直角边对应相等 D.两个锐角对应相等
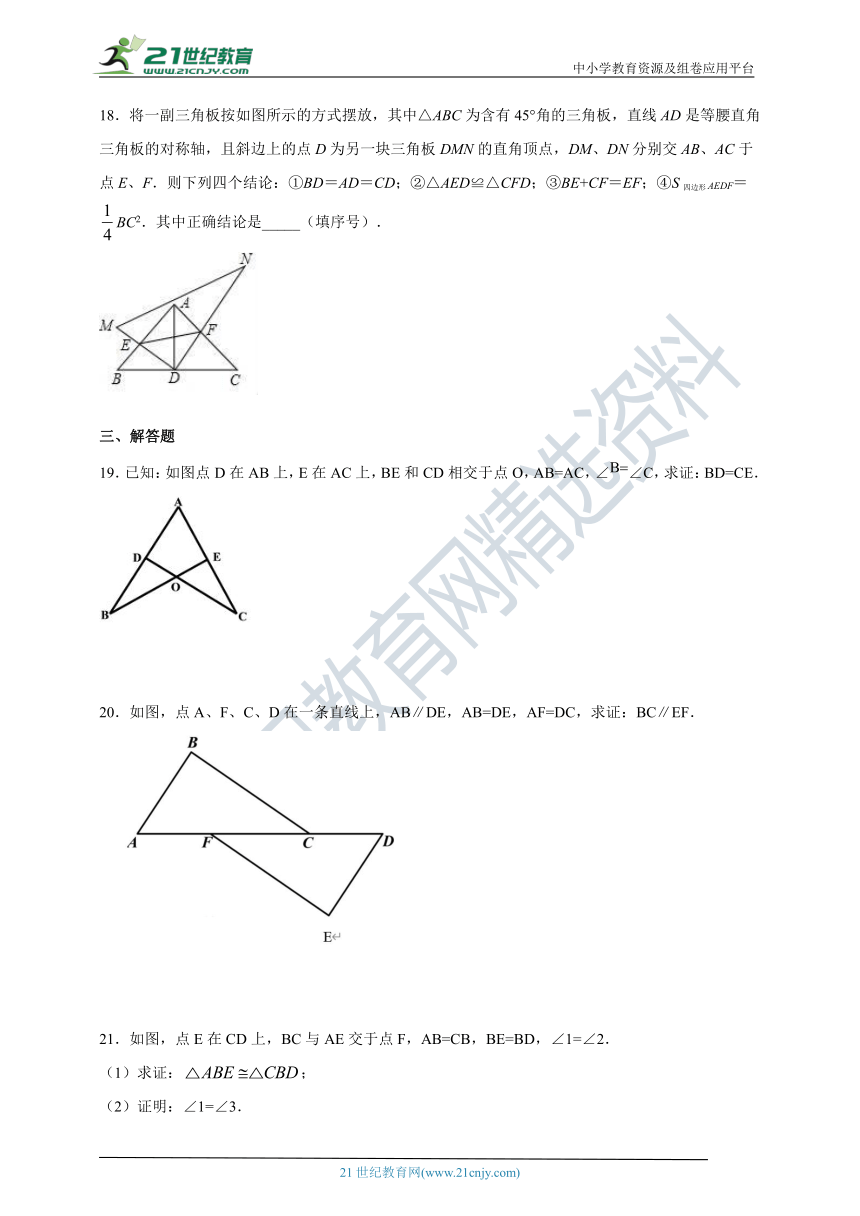
2.如图,OA=OB,OC=OD,AD=BC,则图中全等三角形的对数有( )
A.1对 B.2对 C.3对 D.4对
3.如图,在△ABC中,AB=8,AC=6,AD是BC边上的中线,则AD长的取值范围是( )
A.64.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB= CD
5.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是( )
A.1.5 B.2 ? C.??????????? ? D.
6.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为( )
A.1 B.2 C. D.
7.在和中,,高,则和的关系是( )
A.相等 B.互补
C.相等或互补 D.以上都不对
8.如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( )
A.2种 B.3种 C.4种 D.6种
9.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作 EF∥AD,与AC、DC 分别交于点G,F,H为CG的中点,连结DE、 EH、DH、FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若,则.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
11.已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )
A.6 B.5
C.4.5 D.与AP的长度有关
12.如图,在和中,,连接交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( ).
A.4 B.3 C.2 D.1
二、填空题
13.如图,AB=AD,要证明△ABC与△ADC全等,只需增加的一个条件是______________
14.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在平面直角坐标系中且不与C点重合,若与全等,则点D的坐标是_________.
15.如图,在中,点F在边BC上,于点D,于点E,,,若,则________.
16.如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________
①AD=EC;②BM=BN;③MN∥AC;④EM=MB.
17.如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E, F在射线AC与射线CB上运动,且满足AE=CF,∠EDF=90°;当点E运动到与点C的距离为1时,则△DEF的面积为___________.
18.将一副三角板按如图所示的方式摆放,其中△ABC为含有45°角的三角板,直线AD是等腰直角三角板的对称轴,且斜边上的点D为另一块三角板DMN的直角顶点,DM、DN分别交AB、AC于点E、F.则下列四个结论:①BD=AD=CD;②△AED≌△CFD;③BE+CF=EF;④S四边形AEDF=BC2.其中正确结论是_____(填序号).
三、解答题
19.已知:如图点D在AB上,E在AC上,BE和CD相交于点O,AB=AC,∠∠C,求证:BD=CE.
20.如图,点A、F、C、D在一条直线上,AB∥DE,AB=DE,AF=DC,求证:BC∥EF.
21.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:;
(2)证明:∠1=∠3.
22.如图,在四边形中,,,,,分别是、上的点,且,,,则______.
23.小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?
(1)请你帮他们解答,并说明理由.
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并证明结论.
参考答案
1.D
【详解】
解:A、符合AAS,正确;
B、符合SSS,正确;
C、符合HL,正确;
D、因为判定三角形全等必须有边的参与,错误.
2.C
【详解】
解:∵OA=OB,OC=OD,AD=BC,
∴△DOA≌△COB(SSS);
∵OA=OB,OC=OD,
∴AC=BD,
∵AB=AB,AD=BC,
∴△ABD≌△BAC(SSS);
∵AD=BC,AC=BD,DC=CD
∴△ADC≌△BCD(SSS).
3.C
【详解】
解:延长AD到E,使AD=DE,连接BE,如图所示:
∵AD=DE,∠ADC=∠BDE,BD=DC,
∴△ADC≌△EDB(SAS)
∴BE=AC=6,
在△AEB中,AB-BE<AE<AB+BE,
即8-6<2AD<8+6,
∴1<AD<7,
4.D
【详解】
添加的条件是AB=CD;理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴ (HL).
5.B
【详解】
∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=,
∴∠EBC+∠BCE=,
∵∠BCE+∠ACD=,
∴∠EBC=∠DCA,
在?CEB和?ADC中,∠E=∠ADC,∠EBC=∠DCA,BC=AC,
∴?CEB??ADC(AAS),
∴BE=DC=1,CE=AD=3,
∴DE=EC-CD=3-1=2,
6.B
【详解】
∵AD⊥BC,CE⊥AB,
∴∠BEC=∠ADB=90°,
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BAD=∠BCE,
在△BCE和△HAE中,
,
∴△BCE≌△HAE(AAS),
∴CE=AE=6,
∴CH=CE-HE=6-4=2.
7.C
【解析】
试题解析:当∠C′为锐角时,如图1所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ADC≌Rt△A′D′C′,
∴∠C=∠C′;
当∠C为钝角时,如图3所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ACD≌Rt△A′C′D′,
∴∠C=∠A′C′D′,
∴∠C+∠A′C′B′=180°.
8.C
【详解】
解:有①②,①③,②④,③④,共4种,
①②,
理由是:∵OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠DCO,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形;
①③,
理由是:∵在△EBO和△DCO中 ,
∴△EBO≌△DCO,
∴∠EBO=∠DCO,
∵∠OBC=∠OCB(已证),
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
②④,
理由是:∵在△EBO和△DCO中,
∴△EBO≌△DCO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
③④,
理由是:∵在△EBO和△DCO中,
∴△EBO≌△DCO,
∴∠EBO=∠DCO,OB=OC,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
9.D
【解析】
∵△ABC是等边三角形,PR⊥AB,PS⊥AC,且PR=PS,∴P在∠A的平分线上,故①正确;
由①可知,PB=PC,∠B=∠C,PS=PR,∴△BPR≌△CPS,∴AS=AR,故②正确;
∵AQ=PQ,∴∠PQC=2∠PAC=60°=∠BAC,∴PQ∥AR,故③正确;
由③得,△PQC是等边三角形,∴△PQS≌△PCS,又由②可知,④△BRP≌△QSP,故④也正确,∵①②③④都正确,故选D.
10.D
【详解】
分析:①根据题意可知∠ACD=45°,则GF=FC,则EG=EF-GF=CD-FC=DF;
②由SAS证明△EHF≌△DHC即可;
③根据△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°;
④若=,则AE=2BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=5x,DH=,CD=6x,则S△DHC=×HM×CD=3x2,S△EDH=×DH2=13x2.
详解:①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF?GF,DF=CD?FC,
∴EG=DF,故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=∠GFC=45°=∠HCD,
在△EHF和△DHC中,
EF=CD;∠EFH=∠DCH;FH=CH,
∴△EHF≌△DHC(SAS),故②正确;
③∵△EHF≌△DHC(已证),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF?∠HDC=∠AEF+∠ADF=180°,故③正确;
④∵=,
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,
EG=DF;∠EGH=∠HFD;GH=FH,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
如图,过H点作HM⊥CD于M,
设HM=x,则DM=5x,DH=,CD=6x,
则S△DHC=×HM×CD=3x2,S△EDH=×DH2=13x2,
∴3S△EDH=13S△DHC,故④正确;
11.A
【详解】
解;如图,作DQ⊥AB,交AB的延长线于点F,连接DE,PQ,
又∵PE⊥AB于E,
∴∠BQD=∠AEP=90°,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠DBQ=60°,
在△APE和△BDQ中,
,
∴△APE≌△BDQ(AAS),
∴AE=BQ,PE=QD且PE∥QD,
∴四边形PEDQ是平行四边形,
∴EF=EQ,
∵EB+AE=BE+BQ=AB,
∴EF=AB,
又∵等边△ABC的边长为12,
∴EF=6.
12.B
【详解】
解:∵,
∴,
即,
在和中,,
∴,
∴,①正确;
∴,
由三角形的外角性质得:
∴°,②正确;
作于,于,如图所示:
则°,
在和中,,
∴,
∴,
∴平分,④正确;
正确的个数有3个;
故选B.
13.DC=BC(答案不唯一)
【详解】
解:∵AB=AD,AC=AC
∴要使△ABC≌△ADC可利用SSS判定,
故添加DC=BC(答案不唯一).
故答案为:BC=DC,(答案不唯一).
14.或或
【详解】
解:当D点与C点关于y轴对称时,△ABD与△ABC全等,此时D点坐标为(-4,3);
当点D与点C关于AB的垂直平分线对称时,△ABD与△ABC全等,此时D点坐标为(4,2);
点D点与(4,2)关于y轴对称时,△ABD与△ABC全等,此时D点坐标为(-4,2);
综上所述,D点坐标为(-4,3),(4,2),(-4,2).
故答案为:(-4,3),(4,2),(-4,2).
15.
【详解】
,,
.
在和中,,
,
,
.
16.①②③
【解析】
∵△ABE,△BCD均为等边三角形,
∴AB=BE,BC=BD,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中
∴△ABD≌△EBC(SAS),
∴AD=EC,故①正确;
∴∠DAB=∠BEC,
又由上可知∠ABE=∠CBD=60°,
∴∠EBD=60°,
在△ABM和△EBN中
∴△ABM≌△EBN(ASA),
∴BM=BN,故②正确;
∴△BMN为等边三角形,
∴∠NMB=∠ABM=60°,
∴MN∥AC,故③正确;
若EM=MB,则AM平分∠EAB,
则∠DAB=30°,而由条件无法得出这一条件,
故④不正确;
综上可知正确的有①②③,
17.或
【详解】
解:①E在线段AC上.在△ADE和△CDF中,∵AD=CD,∠A=∠DCF,AE=CF,∴△ADE≌△CDF(SAS),∴同理△CDE≌△BDF,∴四边形CEDF面积是△ABC面积的一半.∵CE=1,∴CF=4﹣1=3,∴△CEF的面积=CE?CF=,∴△DEF的面积=××﹣=.
②E'在AC延长线上.∵AE'=CF',AC=BC=4,∠ACB=90°,∴CE'=BF',∠ACD=∠CBD=45°,CD=AD=BD=,∴∠DCE'=∠DBF'=135°.在△CDE'和△BDF'中,∵CD=BD,∠DCE′=DBF′,CE′=BF′,∴△CDE'≌△BDF'(SAS),∴DE'=DF',∠CDE'=∠BDF'.∵∠CDE'+∠BDE'=90°,∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°.∵DE'2=CE'2+CD2﹣2CD?CE'cos135°=1+8+2××=13,∴S△E'DF'=DE'2=.故答案为或.
18.①②
【解析】
分析:根据等腰直角三角形的性质可得AD=CD=BD,∠CAD=∠B=45°,故①正确;根据同角的余角相等求出∠CDF=∠ADE,然后利用“ASA”证明△ADE≌△CDF,判断出②,根据全等三角形的对应边相等,可得DE=DF=AF=AE,利用三角形的任意两边之和大于第三边,可得BE+CF>EF,判断出③,根据全等三角形的面积相等,可得S△ADF=S△BDE,从而求出四边形AEDF的面积,判断出④.
详解:∵∠B=45°,AB=AC
∴点D为BC的中点,
∴AD=CD=BD
故①正确;
由AD⊥BC,∠BAD=45°
可得∠EAD=∠C
∵∠MDN是直角
∴∠ADF+∠ADE=∠CDF+∠ADF=∠ADC=90°
∴∠ADE=∠CDF
∴△ADE≌△CDF(ASA)
故②正确;
∴DE=DF,AE=CF,
∴AF=BE
∴BE+AE=AF+AE
∴AE+AF>EF
故③不正确;
由△ADE≌△CDF可得S△ADF=S△BDE
∴S四边形AEDF=S△ACD=×AD×CD=×BC×BC=BC2,
故④不正确.
故答案为①②.
19.见解析.
【详解】
在△ABE和△ACD中,
∵
∴△ABE≌△ACD(ASA),
∵AD=AE,
AB=AC,
∴AB-AD=AC-AE,
即:BD=CE.
20.见解析
【详解】
解:证明:,
,
,
.
在与中,
,
,
,
.
21.(1)证明见解析;(2)证明见解析.
【详解】
(1),
,即,
在和中,,
;
(2)由(1)已证:,
,
由对顶角相等得:,
又,
.
22.3
【详解】
解:连接AM,延长FD到M,使DM=BE
∵
∴∠ADM=∠B=90°
在△ABE和△ADM中
AB=AD,∠B=∠ADM,BE=DM
∴△ABE≌△ADM(SAS),
∴AE=AM,∠BAE=∠DAM,
又∵∠BAD=120°,∠EAF=60.
∴∠BAE+∠DAF=60°
∴∠MAF=60°=∠EAF
在AEAF和AMAF中
AF=AF ,∠EAF=∠MAF ,AE=AM
∴△EAF≌△MAF(SAS),
∴EF=FM
∴DF=EF-BE=5-2-3.
23.(1),理由见解析;(2)见解析;(3)见解析
【分析】
(1)根据全等三角形的判定定理证得;
(2)由(1)中的全等三角形的对应角相等证得,则由全等三角形的判定定理证得,则对应边;
(3)同(2),利用全等三角形的对应边相等证得结论.
【详解】
解:(1),理由如下:
如图1,在与中,
,
;
(2)如图2,由(1)知,,则.
在与中,
,
,
;
(3)如图3,.
理由同(2),,则.
_21?????????è?????(www.21cnjy.com)_
人教版2021年八年级上册数学同步练习卷
12.2三角形全等的判断
一、单选题
1.不能使两个直角三角形全等的条件是( ).
A.一条直角边及其对角对应相等 B.斜边和两条直角边对应相等
C.斜边和一条直角边对应相等 D.两个锐角对应相等
2.如图,OA=OB,OC=OD,AD=BC,则图中全等三角形的对数有( )
A.1对 B.2对 C.3对 D.4对
3.如图,在△ABC中,AB=8,AC=6,AD是BC边上的中线,则AD长的取值范围是( )
A.6
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB= CD
5.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是( )
A.1.5 B.2 ? C.??????????? ? D.
6.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为( )
A.1 B.2 C. D.
7.在和中,,高,则和的关系是( )
A.相等 B.互补
C.相等或互补 D.以上都不对
8.如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( )
A.2种 B.3种 C.4种 D.6种
9.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作 EF∥AD,与AC、DC 分别交于点G,F,H为CG的中点,连结DE、 EH、DH、FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若,则.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
11.已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )
A.6 B.5
C.4.5 D.与AP的长度有关
12.如图,在和中,,连接交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( ).
A.4 B.3 C.2 D.1
二、填空题
13.如图,AB=AD,要证明△ABC与△ADC全等,只需增加的一个条件是______________
14.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在平面直角坐标系中且不与C点重合,若与全等,则点D的坐标是_________.
15.如图,在中,点F在边BC上,于点D,于点E,,,若,则________.
16.如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________
①AD=EC;②BM=BN;③MN∥AC;④EM=MB.
17.如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E, F在射线AC与射线CB上运动,且满足AE=CF,∠EDF=90°;当点E运动到与点C的距离为1时,则△DEF的面积为___________.
18.将一副三角板按如图所示的方式摆放,其中△ABC为含有45°角的三角板,直线AD是等腰直角三角板的对称轴,且斜边上的点D为另一块三角板DMN的直角顶点,DM、DN分别交AB、AC于点E、F.则下列四个结论:①BD=AD=CD;②△AED≌△CFD;③BE+CF=EF;④S四边形AEDF=BC2.其中正确结论是_____(填序号).
三、解答题
19.已知:如图点D在AB上,E在AC上,BE和CD相交于点O,AB=AC,∠∠C,求证:BD=CE.
20.如图,点A、F、C、D在一条直线上,AB∥DE,AB=DE,AF=DC,求证:BC∥EF.
21.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:;
(2)证明:∠1=∠3.
22.如图,在四边形中,,,,,分别是、上的点,且,,,则______.
23.小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?
(1)请你帮他们解答,并说明理由.
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并证明结论.
参考答案
1.D
【详解】
解:A、符合AAS,正确;
B、符合SSS,正确;
C、符合HL,正确;
D、因为判定三角形全等必须有边的参与,错误.
2.C
【详解】
解:∵OA=OB,OC=OD,AD=BC,
∴△DOA≌△COB(SSS);
∵OA=OB,OC=OD,
∴AC=BD,
∵AB=AB,AD=BC,
∴△ABD≌△BAC(SSS);
∵AD=BC,AC=BD,DC=CD
∴△ADC≌△BCD(SSS).
3.C
【详解】
解:延长AD到E,使AD=DE,连接BE,如图所示:
∵AD=DE,∠ADC=∠BDE,BD=DC,
∴△ADC≌△EDB(SAS)
∴BE=AC=6,
在△AEB中,AB-BE<AE<AB+BE,
即8-6<2AD<8+6,
∴1<AD<7,
4.D
【详解】
添加的条件是AB=CD;理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴ (HL).
5.B
【详解】
∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=,
∴∠EBC+∠BCE=,
∵∠BCE+∠ACD=,
∴∠EBC=∠DCA,
在?CEB和?ADC中,∠E=∠ADC,∠EBC=∠DCA,BC=AC,
∴?CEB??ADC(AAS),
∴BE=DC=1,CE=AD=3,
∴DE=EC-CD=3-1=2,
6.B
【详解】
∵AD⊥BC,CE⊥AB,
∴∠BEC=∠ADB=90°,
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BAD=∠BCE,
在△BCE和△HAE中,
,
∴△BCE≌△HAE(AAS),
∴CE=AE=6,
∴CH=CE-HE=6-4=2.
7.C
【解析】
试题解析:当∠C′为锐角时,如图1所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ADC≌Rt△A′D′C′,
∴∠C=∠C′;
当∠C为钝角时,如图3所示,
∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,
∴Rt△ACD≌Rt△A′C′D′,
∴∠C=∠A′C′D′,
∴∠C+∠A′C′B′=180°.
8.C
【详解】
解:有①②,①③,②④,③④,共4种,
①②,
理由是:∵OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠DCO,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形;
①③,
理由是:∵在△EBO和△DCO中 ,
∴△EBO≌△DCO,
∴∠EBO=∠DCO,
∵∠OBC=∠OCB(已证),
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
②④,
理由是:∵在△EBO和△DCO中,
∴△EBO≌△DCO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
③④,
理由是:∵在△EBO和△DCO中,
∴△EBO≌△DCO,
∴∠EBO=∠DCO,OB=OC,
∴∠OBC=∠OCB,
∴∠EBO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠ACB,
即AB=AC,
∴△ABC是等腰三角形;
9.D
【解析】
∵△ABC是等边三角形,PR⊥AB,PS⊥AC,且PR=PS,∴P在∠A的平分线上,故①正确;
由①可知,PB=PC,∠B=∠C,PS=PR,∴△BPR≌△CPS,∴AS=AR,故②正确;
∵AQ=PQ,∴∠PQC=2∠PAC=60°=∠BAC,∴PQ∥AR,故③正确;
由③得,△PQC是等边三角形,∴△PQS≌△PCS,又由②可知,④△BRP≌△QSP,故④也正确,∵①②③④都正确,故选D.
10.D
【详解】
分析:①根据题意可知∠ACD=45°,则GF=FC,则EG=EF-GF=CD-FC=DF;
②由SAS证明△EHF≌△DHC即可;
③根据△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°;
④若=,则AE=2BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=5x,DH=,CD=6x,则S△DHC=×HM×CD=3x2,S△EDH=×DH2=13x2.
详解:①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF?GF,DF=CD?FC,
∴EG=DF,故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=∠GFC=45°=∠HCD,
在△EHF和△DHC中,
EF=CD;∠EFH=∠DCH;FH=CH,
∴△EHF≌△DHC(SAS),故②正确;
③∵△EHF≌△DHC(已证),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF?∠HDC=∠AEF+∠ADF=180°,故③正确;
④∵=,
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,
EG=DF;∠EGH=∠HFD;GH=FH,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
如图,过H点作HM⊥CD于M,
设HM=x,则DM=5x,DH=,CD=6x,
则S△DHC=×HM×CD=3x2,S△EDH=×DH2=13x2,
∴3S△EDH=13S△DHC,故④正确;
11.A
【详解】
解;如图,作DQ⊥AB,交AB的延长线于点F,连接DE,PQ,
又∵PE⊥AB于E,
∴∠BQD=∠AEP=90°,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠DBQ=60°,
在△APE和△BDQ中,
,
∴△APE≌△BDQ(AAS),
∴AE=BQ,PE=QD且PE∥QD,
∴四边形PEDQ是平行四边形,
∴EF=EQ,
∵EB+AE=BE+BQ=AB,
∴EF=AB,
又∵等边△ABC的边长为12,
∴EF=6.
12.B
【详解】
解:∵,
∴,
即,
在和中,,
∴,
∴,①正确;
∴,
由三角形的外角性质得:
∴°,②正确;
作于,于,如图所示:
则°,
在和中,,
∴,
∴,
∴平分,④正确;
正确的个数有3个;
故选B.
13.DC=BC(答案不唯一)
【详解】
解:∵AB=AD,AC=AC
∴要使△ABC≌△ADC可利用SSS判定,
故添加DC=BC(答案不唯一).
故答案为:BC=DC,(答案不唯一).
14.或或
【详解】
解:当D点与C点关于y轴对称时,△ABD与△ABC全等,此时D点坐标为(-4,3);
当点D与点C关于AB的垂直平分线对称时,△ABD与△ABC全等,此时D点坐标为(4,2);
点D点与(4,2)关于y轴对称时,△ABD与△ABC全等,此时D点坐标为(-4,2);
综上所述,D点坐标为(-4,3),(4,2),(-4,2).
故答案为:(-4,3),(4,2),(-4,2).
15.
【详解】
,,
.
在和中,,
,
,
.
16.①②③
【解析】
∵△ABE,△BCD均为等边三角形,
∴AB=BE,BC=BD,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中
∴△ABD≌△EBC(SAS),
∴AD=EC,故①正确;
∴∠DAB=∠BEC,
又由上可知∠ABE=∠CBD=60°,
∴∠EBD=60°,
在△ABM和△EBN中
∴△ABM≌△EBN(ASA),
∴BM=BN,故②正确;
∴△BMN为等边三角形,
∴∠NMB=∠ABM=60°,
∴MN∥AC,故③正确;
若EM=MB,则AM平分∠EAB,
则∠DAB=30°,而由条件无法得出这一条件,
故④不正确;
综上可知正确的有①②③,
17.或
【详解】
解:①E在线段AC上.在△ADE和△CDF中,∵AD=CD,∠A=∠DCF,AE=CF,∴△ADE≌△CDF(SAS),∴同理△CDE≌△BDF,∴四边形CEDF面积是△ABC面积的一半.∵CE=1,∴CF=4﹣1=3,∴△CEF的面积=CE?CF=,∴△DEF的面积=××﹣=.
②E'在AC延长线上.∵AE'=CF',AC=BC=4,∠ACB=90°,∴CE'=BF',∠ACD=∠CBD=45°,CD=AD=BD=,∴∠DCE'=∠DBF'=135°.在△CDE'和△BDF'中,∵CD=BD,∠DCE′=DBF′,CE′=BF′,∴△CDE'≌△BDF'(SAS),∴DE'=DF',∠CDE'=∠BDF'.∵∠CDE'+∠BDE'=90°,∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°.∵DE'2=CE'2+CD2﹣2CD?CE'cos135°=1+8+2××=13,∴S△E'DF'=DE'2=.故答案为或.
18.①②
【解析】
分析:根据等腰直角三角形的性质可得AD=CD=BD,∠CAD=∠B=45°,故①正确;根据同角的余角相等求出∠CDF=∠ADE,然后利用“ASA”证明△ADE≌△CDF,判断出②,根据全等三角形的对应边相等,可得DE=DF=AF=AE,利用三角形的任意两边之和大于第三边,可得BE+CF>EF,判断出③,根据全等三角形的面积相等,可得S△ADF=S△BDE,从而求出四边形AEDF的面积,判断出④.
详解:∵∠B=45°,AB=AC
∴点D为BC的中点,
∴AD=CD=BD
故①正确;
由AD⊥BC,∠BAD=45°
可得∠EAD=∠C
∵∠MDN是直角
∴∠ADF+∠ADE=∠CDF+∠ADF=∠ADC=90°
∴∠ADE=∠CDF
∴△ADE≌△CDF(ASA)
故②正确;
∴DE=DF,AE=CF,
∴AF=BE
∴BE+AE=AF+AE
∴AE+AF>EF
故③不正确;
由△ADE≌△CDF可得S△ADF=S△BDE
∴S四边形AEDF=S△ACD=×AD×CD=×BC×BC=BC2,
故④不正确.
故答案为①②.
19.见解析.
【详解】
在△ABE和△ACD中,
∵
∴△ABE≌△ACD(ASA),
∵AD=AE,
AB=AC,
∴AB-AD=AC-AE,
即:BD=CE.
20.见解析
【详解】
解:证明:,
,
,
.
在与中,
,
,
,
.
21.(1)证明见解析;(2)证明见解析.
【详解】
(1),
,即,
在和中,,
;
(2)由(1)已证:,
,
由对顶角相等得:,
又,
.
22.3
【详解】
解:连接AM,延长FD到M,使DM=BE
∵
∴∠ADM=∠B=90°
在△ABE和△ADM中
AB=AD,∠B=∠ADM,BE=DM
∴△ABE≌△ADM(SAS),
∴AE=AM,∠BAE=∠DAM,
又∵∠BAD=120°,∠EAF=60.
∴∠BAE+∠DAF=60°
∴∠MAF=60°=∠EAF
在AEAF和AMAF中
AF=AF ,∠EAF=∠MAF ,AE=AM
∴△EAF≌△MAF(SAS),
∴EF=FM
∴DF=EF-BE=5-2-3.
23.(1),理由见解析;(2)见解析;(3)见解析
【分析】
(1)根据全等三角形的判定定理证得;
(2)由(1)中的全等三角形的对应角相等证得,则由全等三角形的判定定理证得,则对应边;
(3)同(2),利用全等三角形的对应边相等证得结论.
【详解】
解:(1),理由如下:
如图1,在与中,
,
;
(2)如图2,由(1)知,,则.
在与中,
,
,
;
(3)如图3,.
理由同(2),,则.
_21?????????è?????(www.21cnjy.com)_
