11.1.1 三角形的边 课件(共32张PPT)
文档属性
| 名称 | 11.1.1 三角形的边 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 15:39:03 | ||
图片预览









文档简介
11.1.1 三角形的边
第十一章 三角形
2021-2022学年初中数学人教版八年级上册
学习目标
1.结合具体的实例,进一步认识三角形的概念及其基本要素. 2.会用符号、字母表示三角形,并了解按边的相等关系对三角形进行分类. 3.理解三角形任何两边之和大于第三边与任意两边之差小于第三边的性质,并会初步运用这些性质来解决问题.
观察下面几幅图中老师所指的部分有什么共同特点?
看一看
新课导入
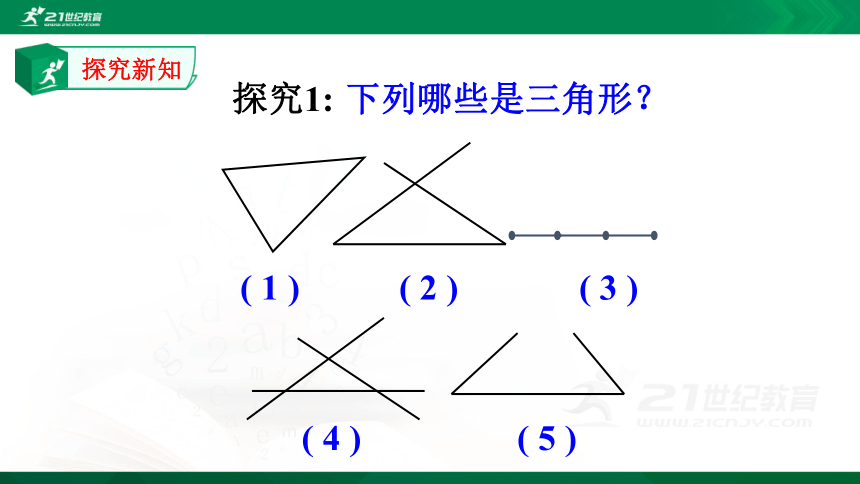
探究1:
下列哪些是三角形?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
探究新知
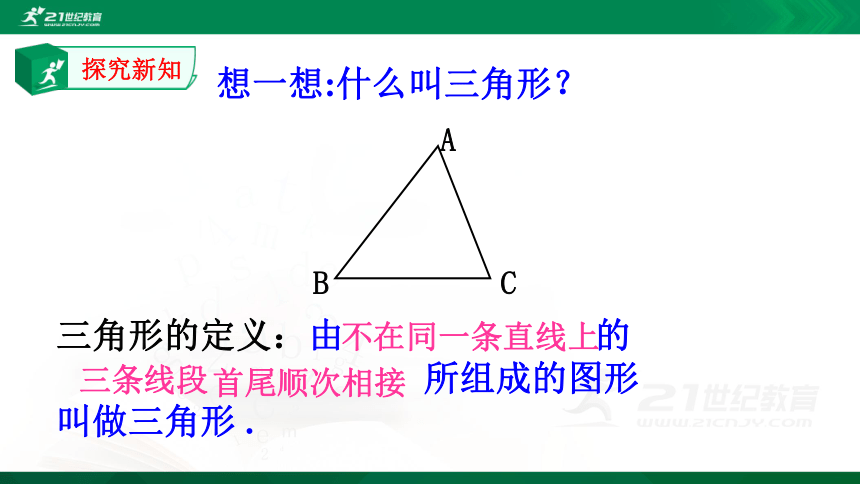
三角形的定义:由 的
所组成的图形
叫做三角形 .
不在同一条直线上
三条线段
首尾顺次相接
A
B
C
想一想:什么叫三角形?
探究新知
A
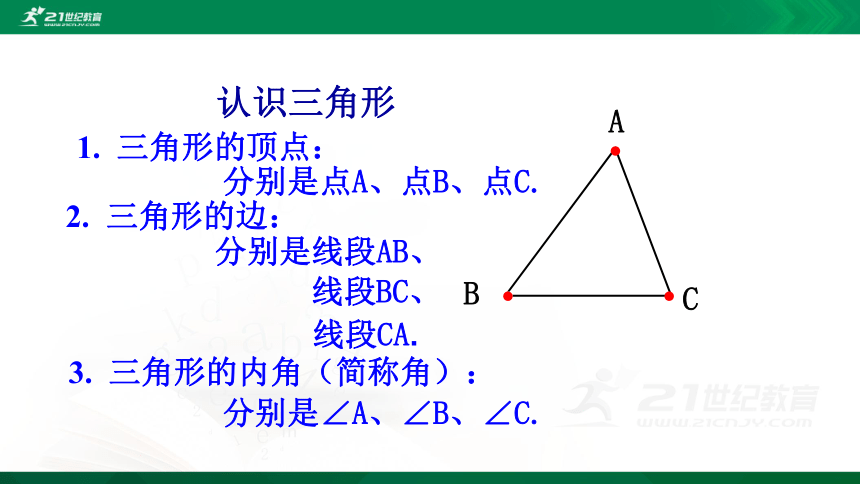
认识三角形
1. 三角形的顶点:
分别是点A、点B、点C.
2. 三角形的边:
分别是线段AB、
3. 三角形的内角(简称角):
分别是∠A、∠B、∠C.
B
C
线段BC、
线段CA.
三 角 形 的 表 示
A
B
C
表示为:
用三个顶点字母表示.
或表示为:△BAC或△ACB.
△ABC
读作:三角形ABC
△ABC的三边,有时也用a,b,c来表示.
一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
三角形边、角的表示
A
B
C
1. 边的表示:
2 角的表示:
c
a
b
∠A,∠B,∠C.
可用一个大写字母、
三个大写字母、希腊字母、数字表示.
线段AB、线段BC、线段CA.
图中的角应表示为:
思考:什么时候用三个大写字母表示?
学以致用:读出图中的各个三角形,并把它们的顶点、边和角表示出来.
A
D
B
E
C
D
B
A
C
1.图中有几个三角形?用符号表示这些三角形.
2.以BD为边的三角形有哪些?
3.以点A为顶点的三角形有哪些?
答:有△ ABD ,△DBC.
分别是:△ ABD ,△ABC,△DBC.
答:有△ ABD ,△ABC.
活学活用:
答:三个.
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形按角分类
旧知回顾
探究2:
观察下列三角形的边,你有什么发现?
不等边三角形
等腰三角形
等边三角形
等腰三角形
探究新知
归纳:
三角形
不等边三角形
等腰三角形
底和腰不相等
的等腰三角形
底和腰相等的
等边三角形
三角形按边分类
巩固
判断下列说法是否正确:
(2)三角形按边分为两类:分别是
等腰三角形和不等边三角形.
(1)三角形按边分为两类:分别是
等腰三角形和等边三角形.
( )
( )
探究3:
蚂蚁要从A点去B点觅食,请你帮
忙选择最佳的路径.
A
B
C
1.从A到B有几条路?
两条.
2.哪条路最近?为什么?
AB
AC
+
BC
>
两点之间线段最短.
BC
AB
+
>
AC
AC
AB
+
>
BC
能用简练的语言说一说这三边的关系吗?
小结:
三角形两边的和大于第三边.
这三个式子同时存在.
路径AB最短.
探究新知
A
C
B
动手试一试:如何填下列空?
小结:三角形两边的差小于第三边.
BC
AB
AC
AC
AB
-
<
BC
AC
-
BC
AB
-
<
<
能用简练的语言说一说三边之间的关系吗?
(1)
(2)
(3)
这三个式子同时存在
归纳
三角形三边关系定理:三角形两边的 和大于第三边.
A
B
C
c
a
b
如:AB+BC>CA
c+a>b
三角形三边关系定理:三角形两边的差小于第三边.
如:AB-BCc-ac-a< b < c + a
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
答:不能.如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以她一步不能走3米多.
做一做!
有三根木棒长分别为3 cm,6 cm,2 cm,它们能否围成三角形?为什么?
你有什么更好的办法吗?
用两条小边之和与大边比较.
用最大边减中边的差与最小边比较.
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3 cm,4 cm,8 cm ( )
(2) 11 ,5,6 ( )
(3) 6,10,5 ( )
不能
不能
能
课堂练习
2.下列长度的三条线段能否组成三角形?为什么?
(1) 3,8,4 ( )
(2) 6,5 ,2 ( )
(3) 5,6,10 ( )
(4) 2,8 ,5 ( )
不能
能
能
不能
课堂练习
4米
3米
别踩我,我怕疼!
5米
A
B
学校草坪弄不好就会走出一条小路来.
其实我们离文明很近!
4
(1米=2步)
他只少走 步.
学以致用
你能不能运用今天所学的知识解释这一现象?
C
能力提升:
在△ABC中,若 a =3,b =7,则第三边 c 的取值范围是 .
既要考虑“两边的和大于第三边”,又要考虑“两边的差小于第三边”.
a - b < c < a + b
在△ABC中,若a =3,b=7,则其周长 l 的取值范围是 .
4 < c < 10
14 < l < 20
三角形
定义
表示方
分类法
三边关
系定理
按边分类
按角分类
a - b < c < a + b
小 结
课堂小结
谢谢聆听
第十一章 三角形
2021-2022学年初中数学人教版八年级上册
学习目标
1.结合具体的实例,进一步认识三角形的概念及其基本要素. 2.会用符号、字母表示三角形,并了解按边的相等关系对三角形进行分类. 3.理解三角形任何两边之和大于第三边与任意两边之差小于第三边的性质,并会初步运用这些性质来解决问题.
观察下面几幅图中老师所指的部分有什么共同特点?
看一看
新课导入
探究1:
下列哪些是三角形?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
探究新知
三角形的定义:由 的
所组成的图形
叫做三角形 .
不在同一条直线上
三条线段
首尾顺次相接
A
B
C
想一想:什么叫三角形?
探究新知
A
认识三角形
1. 三角形的顶点:
分别是点A、点B、点C.
2. 三角形的边:
分别是线段AB、
3. 三角形的内角(简称角):
分别是∠A、∠B、∠C.
B
C
线段BC、
线段CA.
三 角 形 的 表 示
A
B
C
表示为:
用三个顶点字母表示.
或表示为:△BAC或△ACB.
△ABC
读作:三角形ABC
△ABC的三边,有时也用a,b,c来表示.
一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.
三角形边、角的表示
A
B
C
1. 边的表示:
2 角的表示:
c
a
b
∠A,∠B,∠C.
可用一个大写字母、
三个大写字母、希腊字母、数字表示.
线段AB、线段BC、线段CA.
图中的角应表示为:
思考:什么时候用三个大写字母表示?
学以致用:读出图中的各个三角形,并把它们的顶点、边和角表示出来.
A
D
B
E
C
D
B
A
C
1.图中有几个三角形?用符号表示这些三角形.
2.以BD为边的三角形有哪些?
3.以点A为顶点的三角形有哪些?
答:有△ ABD ,△DBC.
分别是:△ ABD ,△ABC,△DBC.
答:有△ ABD ,△ABC.
活学活用:
答:三个.
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形按角分类
旧知回顾
探究2:
观察下列三角形的边,你有什么发现?
不等边三角形
等腰三角形
等边三角形
等腰三角形
探究新知
归纳:
三角形
不等边三角形
等腰三角形
底和腰不相等
的等腰三角形
底和腰相等的
等边三角形
三角形按边分类
巩固
判断下列说法是否正确:
(2)三角形按边分为两类:分别是
等腰三角形和不等边三角形.
(1)三角形按边分为两类:分别是
等腰三角形和等边三角形.
( )
( )
探究3:
蚂蚁要从A点去B点觅食,请你帮
忙选择最佳的路径.
A
B
C
1.从A到B有几条路?
两条.
2.哪条路最近?为什么?
AB
AC
+
BC
>
两点之间线段最短.
BC
AB
+
>
AC
AC
AB
+
>
BC
能用简练的语言说一说这三边的关系吗?
小结:
三角形两边的和大于第三边.
这三个式子同时存在.
路径AB最短.
探究新知
A
C
B
动手试一试:如何填下列空?
小结:三角形两边的差小于第三边.
BC
AB
AC
AC
AB
-
<
BC
AC
-
BC
AB
-
<
<
能用简练的语言说一说三边之间的关系吗?
(1)
(2)
(3)
这三个式子同时存在
归纳
三角形三边关系定理:三角形两边的 和大于第三边.
A
B
C
c
a
b
如:AB+BC>CA
c+a>b
三角形三边关系定理:三角形两边的差小于第三边.
如:AB-BC
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
答:不能.如果此人一步能走3米多,由三角形三边的关系得,此人两腿得长大于3米多,这与实际情况相矛盾,所以她一步不能走3米多.
做一做!
有三根木棒长分别为3 cm,6 cm,2 cm,它们能否围成三角形?为什么?
你有什么更好的办法吗?
用两条小边之和与大边比较.
用最大边减中边的差与最小边比较.
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3 cm,4 cm,8 cm ( )
(2) 11 ,5,6 ( )
(3) 6,10,5 ( )
不能
不能
能
课堂练习
2.下列长度的三条线段能否组成三角形?为什么?
(1) 3,8,4 ( )
(2) 6,5 ,2 ( )
(3) 5,6,10 ( )
(4) 2,8 ,5 ( )
不能
能
能
不能
课堂练习
4米
3米
别踩我,我怕疼!
5米
A
B
学校草坪弄不好就会走出一条小路来.
其实我们离文明很近!
4
(1米=2步)
他只少走 步.
学以致用
你能不能运用今天所学的知识解释这一现象?
C
能力提升:
在△ABC中,若 a =3,b =7,则第三边 c 的取值范围是 .
既要考虑“两边的和大于第三边”,又要考虑“两边的差小于第三边”.
a - b < c < a + b
在△ABC中,若a =3,b=7,则其周长 l 的取值范围是 .
4 < c < 10
14 < l < 20
三角形
定义
表示方
分类法
三边关
系定理
按边分类
按角分类
a - b < c < a + b
小 结
课堂小结
谢谢聆听
