四川省成都市树德协进中学2011-2012学年高二下学期期中考试数学试题
文档属性
| 名称 | 四川省成都市树德协进中学2011-2012学年高二下学期期中考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-02 00:00:00 | ||
图片预览




文档简介
一.选择题(以下各题只有一个正确答案,每小题5分,共60分)
1. 某学校有教师人,其中高级教师人,中级教师人,初级教师人. 现按职称分层抽样选出名教师参加教工代表大会,则选出的高、中、初级教师的人数分别为 ( )
A. B. C. D.
2.命题,,命题,,则下列命题中真命题是 ( )
(A)(B)(C)(D)
3.在极坐标系中,过点且平行于极轴的直线的极坐标方程是( )
(A) (B)
(C) (D)
4.在平面直角坐标系中,点的直角坐标为.若以原点为极点,x轴正半轴为极轴建立极坐标系,则点的极坐标可以是 ( )
(A) (B) (C) (D)
5、某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,那么互斥不对立的两个事件是:( )
A、至少有1名男生与全是女生 B、至少有1名男生与全是男生
C、至少有1名男生与至少有1名女生 D、恰有1名男生与恰有2名女生
6(理科做).甲从正四面体的四个顶点中任意选择两个顶点连成直线,乙从该正四面体四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是 ( )
A. B. C. D.
6、(文科做)从写上0,1,2,…,9 十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片数字各不相同的概率是( )
A. B. C. D. 1
7.要将一根长为60cm的木棒截成两段,有一段小于15cm的概率是:( )
A、 B、 C、 D、
8.(理科做).命题“存在,使<0,为假命题”是命题“”的 ( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
8.(文科做).如果,那么“∥”是“”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
9.(理科做).曲线上的点到直线的最短距离是( )
A. B. C. D. 0
9.(文科做)函数的最大值为( )
A. B. C. D.
10.函数f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0成立,则a的取值为 ( )
A.[2,+∞) B.[4,+∞)
C.{4} D.[2,4]
11(理科做).方程的实根个数是( )
A.3 B.2 C.1 D.0
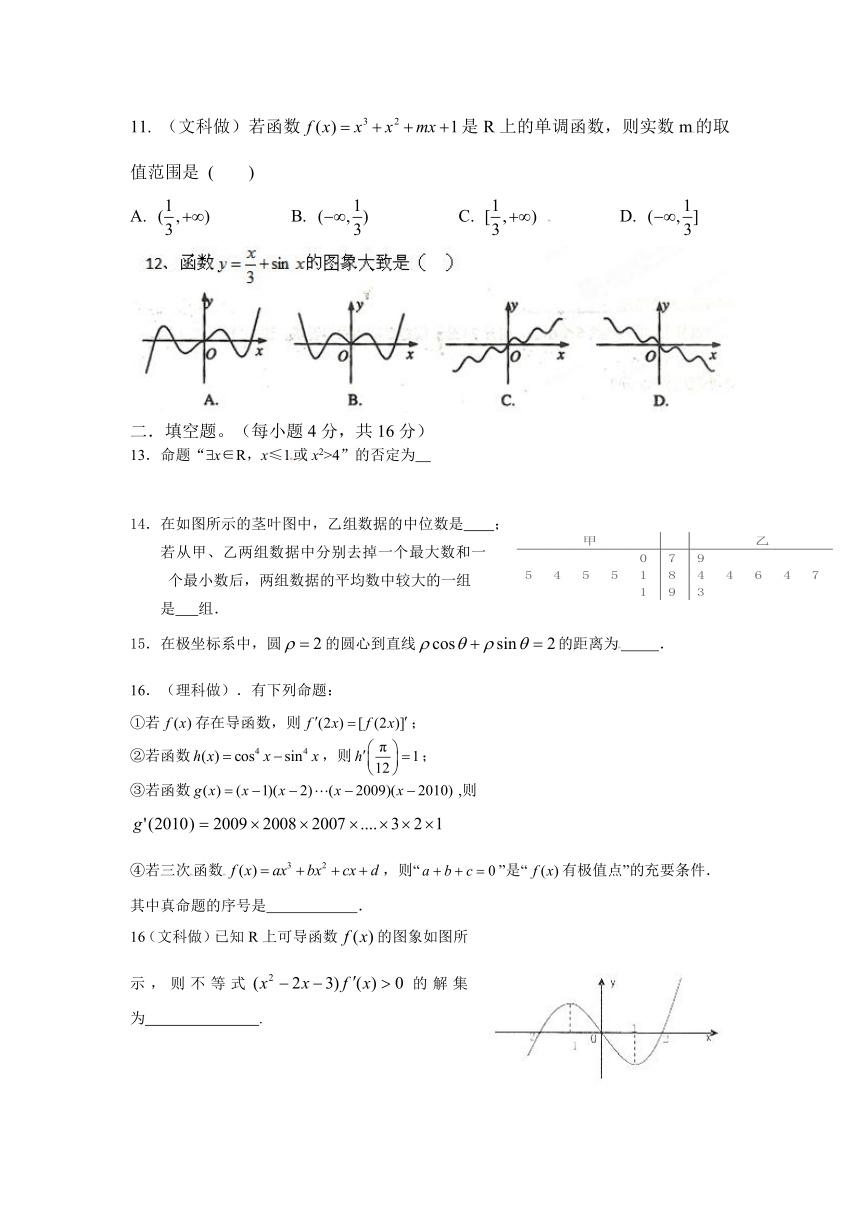
11. (文科做)若函数是R上的单调函数,则实数m的取值范围是 ( )
A. B. C. D.
二.填空题。(每小题4分,共16分)
13.命题“x∈R,x≤1或x2>4”的否定为
14.在如图所示的茎叶图中,乙组数据的中位数是 ;
若从甲、乙两组数据中分别去掉一个最大数和一个最小数后,两组数据的平均数中较大的一组
是 组.
15.在极坐标系中,圆的圆心到直线的距离为 .
16.(理科做).有下列命题:
①若存在导函数,则;
②若函数,则;
③若函数,则
④若三次函数,则“”是“有极值点”的充要条件.
其中真命题的序号是 .
16(文科做)已知R上可导函数的图象如图所示,则不等式的解集为 .
三.解答题(17-20每题12分,21-22每题13分)
17.我区高三期末统一测试中某校的数学成绩分组统计如下表:
分组 频数 频率
合计
(Ⅰ)求出表中、、、的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
(Ⅱ)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩
在分以上的人数;
(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求
被选中2人分数不超过30分的概率
.
18.已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
19(理科做) 已知关于的一元二次函数
(Ⅰ)设集合和,分别从集合和中随机取一个数作为和,求函数在区间[上是增函数的概率;
(Ⅱ)设点是区域内的随机点,记有两个零点,其中一个大于,另一个小于,求事件发生的概率。
.
19(文科做)、口袋中有大小、形状都相同的八个球,其中白球3个,红球5个,
(1)任取一个球投在一个面积为的正方形内,求球落在正方形内切圆内
概率;
(2)若在袋中任取两个,求取到红球的概率。
20.一出租车每小时耗油的费用与其车速的立方成正比,当车速为时,该车耗油
费用为/h,其他费用为12元/h.甲乙两地的公路里程为160km,在不考虑其他因素的
提下,为了使该车开往乙地的总费用最低,该车的车速应当确定为多少公里/小时?
21(理科做)已知函数 .
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行,求a的值;
(Ⅱ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅲ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
21(文科做).已知函数 。
(Ⅰ) 若点(1,)在函数图象上且函数在该点处的切线斜率为-4,求的极大值;
(Ⅱ)若在区间[-1,2]上是单调减函数,求的最小值。
22(理科做)22.已知函数为自然对数的底数)
(1)求的单调区间,若有最值,请求出最值;
(2)是否存在正常数,使的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
高考资源网
22(文科做)已知函数 .(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行,求a的值;
(Ⅱ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅲ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
2013级半期考试数学答案
一.选择题 1b2d3a4a5d6(理)a6(文)a7b8(理)b8(文)b9(理)b9(文)a10b11(理)c11(文)c12c
二.填空题
13.x∈R,x>1且x2≤4
18.若方程x2+mx+1=0有两不等的负根,则解得m>2
即p:m>2
若方程4x2+4(m-2)x+1=0无实根
则Δ=16(m-2)2-16=16(m2-4m+3)<0
解得:1<m<3.即q:1<m<3.
因“p或q”为真,所以p、q至少有一为真,又“p且q”为假,所以p、q至少有一为假,
因此,p、q两命题应一真一假,即p为真,q为假或p为假,q为真.
∴
解得: m≥3或1<m≤2.
19.(理科做)18.解析:(Ⅰ)∵函数的图象的对称轴为
要使在区间上为增函数,
当且仅当且 ………………………………2分
若则,若则若则 ……………………4分
记函数在区间上是增函数
则事件包含基本事件的个数是1+2+2=5,∴……6分
(Ⅱ)依条件可知试验的全部结果所构成的区域为,
其面积 ……………………………………8分
事件构成的区域:
由,得交点坐标为………………………………10分
,∴事件发生的概率为
19(文科做)解:(1)圆面积为,设“落在圆内”为事件则
(2)设“取到红球”为事件则 为“两个都为白球”
实验“在袋中任取两个”共有基本事件28个,“两个都为白球”包含三个基本事件则所以P()=,P()=
答为了使这辆出租车由甲地开往乙地得总费用最低。该车得速度应确定为
21(理科).解:(Ⅰ), ……………………1分
, ……………………2分
因为曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行
所以, ……………………3分
所以. ……………………4分
(Ⅱ)令, ……………………5分
即,所以 或. ……………………6分
因为a>0,所以不在区间(a,a2-3)内,
要使函数在区间(a,a 2-3)上存在极值,只需. ……………………7分
所以. ……………………9分
(Ⅲ)证明:令,所以 或.
因为a>2,所以2a>4, ……………………10分
所以在(0,2)上恒成立,函数f(x)在(0,2)内单调递减.
又因为,, ……………………11分
所以f(x)在(0,2)上恰有一个零点. ……………………13分
21(文科)解:(Ⅰ)∵, 1分
∴ 由题意可知:且,
∴ 得: , 3分
∴,.
令,得,
由此可知:
X (-∞,-1) -1 (-1, 3) 3 (3, +∞)
+ 0 - 0 +
↗ 极大值 ↘ 极小值 ↗
∴ 当x=-1时, f(x)取极大值 6分
(Ⅱ) ∵在区间[-1,2]上是单调减函数,
∴ 在区间[-1,2]上恒成立. 7分
根据二次函数图象可知且,
即:也即 9分
作出不等式组表示的平面区域如图: 11分
当直线经过交点P(-, 2)时,
取得最小值, 13分
∴取得最小值为 14分
(2)方法一,若与的图象有且只有一个公共点,
则方程有且只有一解,所以函数有且只有一个零点…………8分
由(1)的结论可知…………10分
此时,
的图象的唯一公共点坐标为
又的图象在点处有共同的切线,
其方程为,即…………13分
综上所述,存在,使的图象有且只有一个公共点,且在该点处的公切线方程为…………14分
方法二:设图象的公共点坐标为,
根据题意得即
由②得,代入①得 从而…………10分
此时由(1)可知 时,
因此除外,再没有其它,使…………13分
故存在,使的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为,公切线方程为…………14分高考资源网
22(文科).解:(Ⅰ), ……………………1分
, ……………………2分
因为曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行
所以, ……………………3分
所以. ……………………4分
(Ⅱ)令, ……………………5分
即,所以 或. ……………………6分
因为a>0,所以不在区间(a,a2-3)内,
要使函数在区间 (a,a 2-3)上存在极值,只需. ……………………7分
所以. ……………………9分
(Ⅲ)证明:令,所以 或.
因为a>2,所以2a>4, ……………………10分
所以在(0,2)上恒成立,函数f(x)在(0,2)内单调递减.
又因为,, ……………………11分
所以f(x)在(0,2)上恰有一个零点. ……………………13分
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.010
0.011
0.012
0.013
0.014
0.015
0.016
分数
频率/组距
30
60
90
120
150
o
a
b
P(-, 2)
4a-b+4=0
2a+b-1=0
z=a+b
-2
2
4
高考资源网高考高·考¥资%源~网资源网
1. 某学校有教师人,其中高级教师人,中级教师人,初级教师人. 现按职称分层抽样选出名教师参加教工代表大会,则选出的高、中、初级教师的人数分别为 ( )
A. B. C. D.
2.命题,,命题,,则下列命题中真命题是 ( )
(A)(B)(C)(D)
3.在极坐标系中,过点且平行于极轴的直线的极坐标方程是( )
(A) (B)
(C) (D)
4.在平面直角坐标系中,点的直角坐标为.若以原点为极点,x轴正半轴为极轴建立极坐标系,则点的极坐标可以是 ( )
(A) (B) (C) (D)
5、某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,那么互斥不对立的两个事件是:( )
A、至少有1名男生与全是女生 B、至少有1名男生与全是男生
C、至少有1名男生与至少有1名女生 D、恰有1名男生与恰有2名女生
6(理科做).甲从正四面体的四个顶点中任意选择两个顶点连成直线,乙从该正四面体四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是 ( )
A. B. C. D.
6、(文科做)从写上0,1,2,…,9 十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片数字各不相同的概率是( )
A. B. C. D. 1
7.要将一根长为60cm的木棒截成两段,有一段小于15cm的概率是:( )
A、 B、 C、 D、
8.(理科做).命题“存在,使<0,为假命题”是命题“”的 ( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
8.(文科做).如果,那么“∥”是“”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
9.(理科做).曲线上的点到直线的最短距离是( )
A. B. C. D. 0
9.(文科做)函数的最大值为( )
A. B. C. D.
10.函数f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0成立,则a的取值为 ( )
A.[2,+∞) B.[4,+∞)
C.{4} D.[2,4]
11(理科做).方程的实根个数是( )
A.3 B.2 C.1 D.0
11. (文科做)若函数是R上的单调函数,则实数m的取值范围是 ( )
A. B. C. D.
二.填空题。(每小题4分,共16分)
13.命题“x∈R,x≤1或x2>4”的否定为
14.在如图所示的茎叶图中,乙组数据的中位数是 ;
若从甲、乙两组数据中分别去掉一个最大数和一个最小数后,两组数据的平均数中较大的一组
是 组.
15.在极坐标系中,圆的圆心到直线的距离为 .
16.(理科做).有下列命题:
①若存在导函数,则;
②若函数,则;
③若函数,则
④若三次函数,则“”是“有极值点”的充要条件.
其中真命题的序号是 .
16(文科做)已知R上可导函数的图象如图所示,则不等式的解集为 .
三.解答题(17-20每题12分,21-22每题13分)
17.我区高三期末统一测试中某校的数学成绩分组统计如下表:
分组 频数 频率
合计
(Ⅰ)求出表中、、、的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
(Ⅱ)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩
在分以上的人数;
(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求
被选中2人分数不超过30分的概率
.
18.已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
19(理科做) 已知关于的一元二次函数
(Ⅰ)设集合和,分别从集合和中随机取一个数作为和,求函数在区间[上是增函数的概率;
(Ⅱ)设点是区域内的随机点,记有两个零点,其中一个大于,另一个小于,求事件发生的概率。
.
19(文科做)、口袋中有大小、形状都相同的八个球,其中白球3个,红球5个,
(1)任取一个球投在一个面积为的正方形内,求球落在正方形内切圆内
概率;
(2)若在袋中任取两个,求取到红球的概率。
20.一出租车每小时耗油的费用与其车速的立方成正比,当车速为时,该车耗油
费用为/h,其他费用为12元/h.甲乙两地的公路里程为160km,在不考虑其他因素的
提下,为了使该车开往乙地的总费用最低,该车的车速应当确定为多少公里/小时?
21(理科做)已知函数 .
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行,求a的值;
(Ⅱ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅲ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
21(文科做).已知函数 。
(Ⅰ) 若点(1,)在函数图象上且函数在该点处的切线斜率为-4,求的极大值;
(Ⅱ)若在区间[-1,2]上是单调减函数,求的最小值。
22(理科做)22.已知函数为自然对数的底数)
(1)求的单调区间,若有最值,请求出最值;
(2)是否存在正常数,使的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
高考资源网
22(文科做)已知函数 .(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行,求a的值;
(Ⅱ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅲ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
2013级半期考试数学答案
一.选择题 1b2d3a4a5d6(理)a6(文)a7b8(理)b8(文)b9(理)b9(文)a10b11(理)c11(文)c12c
二.填空题
13.x∈R,x>1且x2≤4
18.若方程x2+mx+1=0有两不等的负根,则解得m>2
即p:m>2
若方程4x2+4(m-2)x+1=0无实根
则Δ=16(m-2)2-16=16(m2-4m+3)<0
解得:1<m<3.即q:1<m<3.
因“p或q”为真,所以p、q至少有一为真,又“p且q”为假,所以p、q至少有一为假,
因此,p、q两命题应一真一假,即p为真,q为假或p为假,q为真.
∴
解得: m≥3或1<m≤2.
19.(理科做)18.解析:(Ⅰ)∵函数的图象的对称轴为
要使在区间上为增函数,
当且仅当且 ………………………………2分
若则,若则若则 ……………………4分
记函数在区间上是增函数
则事件包含基本事件的个数是1+2+2=5,∴……6分
(Ⅱ)依条件可知试验的全部结果所构成的区域为,
其面积 ……………………………………8分
事件构成的区域:
由,得交点坐标为………………………………10分
,∴事件发生的概率为
19(文科做)解:(1)圆面积为,设“落在圆内”为事件则
(2)设“取到红球”为事件则 为“两个都为白球”
实验“在袋中任取两个”共有基本事件28个,“两个都为白球”包含三个基本事件则所以P()=,P()=
答为了使这辆出租车由甲地开往乙地得总费用最低。该车得速度应确定为
21(理科).解:(Ⅰ), ……………………1分
, ……………………2分
因为曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行
所以, ……………………3分
所以. ……………………4分
(Ⅱ)令, ……………………5分
即,所以 或. ……………………6分
因为a>0,所以不在区间(a,a2-3)内,
要使函数在区间(a,a 2-3)上存在极值,只需. ……………………7分
所以. ……………………9分
(Ⅲ)证明:令,所以 或.
因为a>2,所以2a>4, ……………………10分
所以在(0,2)上恒成立,函数f(x)在(0,2)内单调递减.
又因为,, ……………………11分
所以f(x)在(0,2)上恰有一个零点. ……………………13分
21(文科)解:(Ⅰ)∵, 1分
∴ 由题意可知:且,
∴ 得: , 3分
∴,.
令,得,
由此可知:
X (-∞,-1) -1 (-1, 3) 3 (3, +∞)
+ 0 - 0 +
↗ 极大值 ↘ 极小值 ↗
∴ 当x=-1时, f(x)取极大值 6分
(Ⅱ) ∵在区间[-1,2]上是单调减函数,
∴ 在区间[-1,2]上恒成立. 7分
根据二次函数图象可知且,
即:也即 9分
作出不等式组表示的平面区域如图: 11分
当直线经过交点P(-, 2)时,
取得最小值, 13分
∴取得最小值为 14分
(2)方法一,若与的图象有且只有一个公共点,
则方程有且只有一解,所以函数有且只有一个零点…………8分
由(1)的结论可知…………10分
此时,
的图象的唯一公共点坐标为
又的图象在点处有共同的切线,
其方程为,即…………13分
综上所述,存在,使的图象有且只有一个公共点,且在该点处的公切线方程为…………14分
方法二:设图象的公共点坐标为,
根据题意得即
由②得,代入①得 从而…………10分
此时由(1)可知 时,
因此除外,再没有其它,使…………13分
故存在,使的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为,公切线方程为…………14分高考资源网
22(文科).解:(Ⅰ), ……………………1分
, ……………………2分
因为曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行
所以, ……………………3分
所以. ……………………4分
(Ⅱ)令, ……………………5分
即,所以 或. ……………………6分
因为a>0,所以不在区间(a,a2-3)内,
要使函数在区间 (a,a 2-3)上存在极值,只需. ……………………7分
所以. ……………………9分
(Ⅲ)证明:令,所以 或.
因为a>2,所以2a>4, ……………………10分
所以在(0,2)上恒成立,函数f(x)在(0,2)内单调递减.
又因为,, ……………………11分
所以f(x)在(0,2)上恰有一个零点. ……………………13分
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.010
0.011
0.012
0.013
0.014
0.015
0.016
分数
频率/组距
30
60
90
120
150
o
a
b
P(-, 2)
4a-b+4=0
2a+b-1=0
z=a+b
-2
2
4
高考资源网高考高·考¥资%源~网资源网
同课章节目录
