3.1重力与弹力第2课时 讲义-2020-2021学年【新教材】人教版(2019)高中物理必修第一册word版含答案
文档属性
| 名称 | 3.1重力与弹力第2课时 讲义-2020-2021学年【新教材】人教版(2019)高中物理必修第一册word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 115.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-07-10 12:00:56 | ||
图片预览


文档简介
第三章相互作用——力
第1节重力与弹力第2课时
【素养目标】
1.了解形变、弹性形变、弹性限度等概念.
2.知道弹力产生的原因和条件
3.知道压力、支持力和绳的拉力都是弹力,会分析弹力的方向
4.理解胡克定律,并能解决有关问题
【必备知识】
知识点一、形变
1.形变
(1)形变:物体在力的作用下形状或体积的变化.
(2)弹性形变:物体形变后撤去作用力时能够恢复原状的形变.
(3)弹性限度
当形变超过一定限度时,撤去作用力后物体不能完全恢复原来的形状,这个限度叫弹性限度.
知识点二、弹力
(1)定义:发生形变的物体,由于要恢复原状,对与它接触的物体产生的力.
(2)方向
①压力和支持力的方向垂直于物体的接触面.
②绳的拉力沿着绳而指向绳收缩的方向.
弹力的方向
类型
方向
图示
接触方式
面与面
垂直公共接触面指向被支持物体
点与面
过点垂直于面指向被支持物体
点与点
垂直于公共切面指向受力物体且力的作用线一定过球(圆)心
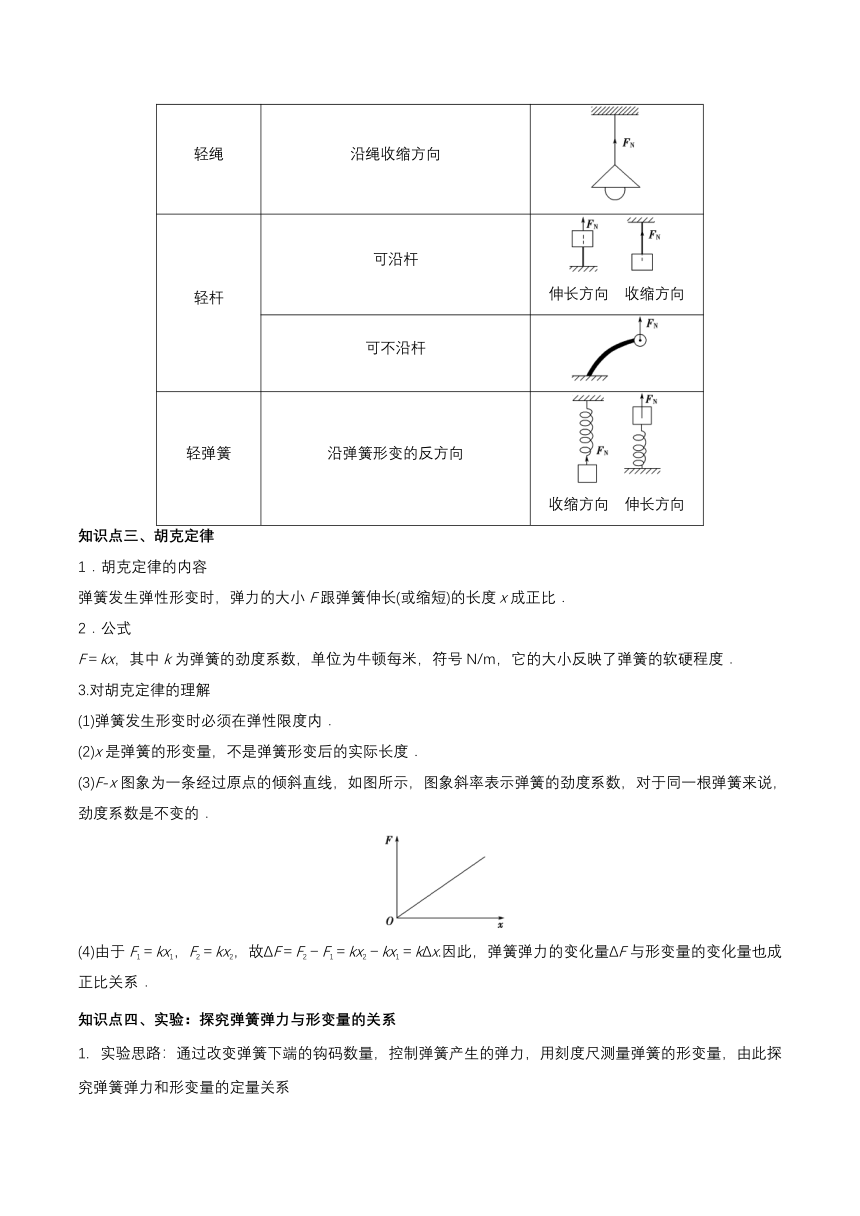
轻绳
沿绳收缩方向
轻杆
可沿杆
伸长方向 收缩方向
可不沿杆
轻弹簧
沿弹簧形变的反方向
收缩方向 伸长方向
知识点三、胡克定律
1.胡克定律的内容
弹簧发生弹性形变时,弹力的大小F跟弹簧伸长(或缩短)的长度x成正比.
2.公式
F=kx,其中k为弹簧的劲度系数,单位为牛顿每米,符号N/m,它的大小反映了弹簧的软硬程度.
3.对胡克定律的理解
(1)弹簧发生形变时必须在弹性限度内.
(2)x是弹簧的形变量,不是弹簧形变后的实际长度.
(3)F?x图象为一条经过原点的倾斜直线,如图所示,图象斜率表示弹簧的劲度系数,对于同一根弹簧来说,劲度系数是不变的.
(4)由于F1=kx1,F2=kx2,故ΔF=F2-F1=kx2-kx1=kΔx.因此,弹簧弹力的变化量ΔF与形变量的变化量也成正比关系.
知识点四、实验:探究弹簧弹力与形变量的关系
实验思路:通过改变弹簧下端的钩码数量,控制弹簧产生的弹力,用刻度尺测量弹簧的形变量,由此探究弹簧弹力和形变量的定量关系
实验过程
将弹簧的一端固定在铁架台的横杆上,让其自由下垂,用刻度尺测出弹簧自然状态的长度,即原长。
将钩码悬挂在弹簧的下端,平衡时测量弹簧的总长度,并计算钩码受到的重力,弹簧的弹力等于钩码的重力。
改变所挂钩码的个数,重复实验过程多次
数据分析
以弹力F为纵轴,以弹力的伸长量x(x=)为横轴,用描点法作图,得出弹力F随弹簧伸长量x变化的图线。
另一种图像
若作F-L图像(L为弹簧总长),由F=kx=k()知,图像的斜率表示劲数系数k,横轴截距表示弹簧原长
【课堂检测】
1.如图所示,重为2N的物体悬挂在弹簧的下端,静止时弹簧伸长了4cm。现换用另一物体悬挂在弹簧的下端,静止时弹簧伸长了6cm(形变仍在弹性限度内),则弹簧的劲度系数和第二种情况下弹力的大小分别是(??
)
A.?50N/m,3N??????????????????B.?100N/m,6N??????????????????C.?50N/m,6N??????????????????D.?100N/m,3N
【答案】
A
【解析】重为2N的物体悬挂在弹簧的下端时,根据物体平衡条件可知,弹簧的弹力F=2N,弹簧伸长的长度x=4cm=4×10?2m。根据胡克定律F=kx
得,
。当弹簧伸长了
时,弹簧的弹力
。
故答案为:A。
【分析】利用物体的平衡方程可以求出弹簧劲度系数的大小;结合弹簧的伸长量及劲度系数的大小可以求出弹簧的弹力大小。
2.如图所示的装置中,A、B两物块的质量分别是
、
,弹簧和绳的质量均不计,绳与滑轮间的摩擦不计,重力加速度
,则下列说法正确的是(??
)
A.?固定物块A,物块B处于静止状态时,弹簧的弹力大小为20N
B.?固定物块B,物块A处于静止状态时,弹簧的弹力大小为30N
C.?先固定物块A,待A,B均静止时再释放A,释放的瞬间弹簧的弹力大小为10N
D.?物块A,B和弹簧一起稳定运动的过程中,弹簧的弹力大小为15N
【答案】
C
【解析】A.固定物块A,B处于平衡状态,根据平衡条件,可知弹簧的弹力大小等于B的重力大小,为10N,A不符合题意;
B.固定物块B,A处于平衡状态,根据平衡条件,可知弹簧的弹力大小等于A的重力大小,为20N,B不符合题意;
C.先固定物块A,由B项分析,可知弹簧的弹力大小为10N,在释放物块A的一瞬间,弹簧的弹力大小不变,仍为10N,C符合题意;
D.物块A、B和弹簧一起稳定运动的过程中,根据牛顿第二定律,对A有:
对B有:
联立解得弹簧的弹力大小
N,D不符合题意。
故答案为:C。
【分析】当绳子剪断后,其中一侧的拉力瞬间消失,但是由于弹簧来不及被压缩,故弹力不变。
【素养作业】
1.东汉时期《考工记·弓人》中记载“假令弓力胜三石,引之中三尺,弛其弦,以绳缓擐之,每加物一石,则张一尺”这表明,在弹性限度内(??
)
A.?弓的弹力与弓的形变量成正比?????????????????????????????B.?弓的弹力与弓的形变量成反比
C.?弓的弹力与弓的形变量的平方成正比??????????????????D.?弓的弹力与弓的形变量的平方成反比
【答案】
A
【解析】根据题意可知:每加物一石,则张一尺,说明每增加一石物体的重力,则形变量改变一尺,故说明在弹性限度内,弓的弹力与弓的形变量成正比,BCD不符合题意,A符合题意。
故答案为:A。
【分析】弹性体在发生弹性形变时,弹性体的弹力F和弹簧的伸长量(或压缩量)x成正比,即F=
kx
,k是物质的弹性系数。
2.某弹簧的劲度系数k=5×103N/m,在弹性限度内,当它伸长2.5cm时,产生的弹力是(?
)
A.?125N????????????????????????????????????B.?50N????????????????????????????????????C.?5N????????????????????????????????????D.?12.5N
【答案】
A
【解析】根据胡克定律:
,A符合题意,BCD不符合题意。
故答案为:A
【分析】结合弹簧的进度系数和形变量,利用胡克定律求解弹力。
3.如图所示,一根劲度系数为k的轻弹簧原长为x0,下端挂上钩码后长度为x1,则弹簧弹力的大小为(??
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
【答案】
D
【解析】由胡克定律F=kx可知,弹簧的弹力F=k(x1-x0),
故答案为:D.
【分析】本题考查胡克定律公式的应用,解题时一定要明确公式中的x为弹簧的形变量,不是原长.
4.图所示,在一张大桌子上放两个平面镜N和M,让一束光依次被两面镜子反射,最后射到墙上,形成一个光点P。用力压桌面时观察墙上光点位置的变化。下列说法中正确的是(??
)
A.?装置中平面镜的作用是通过光的反射把桌面形变放大,便于观察
B.?力F越小,光点P下移越多
C.?力F越小,光点P上移越多
D.?桌面受到的压力,是由于桌面的形变产生的
【答案】
A
【解析】A.
力的作用效果之一就是会使物体发生形变,但硬度越大的物体,其形变越不容易被觉察,为了证实硬度再大的物体在力的作用下也是有发生形变,可采用上图所示的装置进行验证。该装置是一种显示微小形变的装置,它可以把微小形变“放大”到直接看出来,A符合题意;
BC.
若在两镜之间桌面用力F下压,M、N将向中间倾斜,增大压力,则光束的入射角减小,由光的反射定律可知,光点会在刻度尺上从P点向下移动其力越大,移动越明显,力F越小,光点P下移越小。B不符合题意,C不符合题意;
D.
桌面受到的压力,是由施力物体发生形变产生的,而桌面是受力物体,D不符合题意;
故答案为:A。
【分析】物理学中用到的试验方法有很多,质点和点电荷是同一种思想方法,加速度、电场强度、电势都是采取比值法定义的物理量,重心、合力和分力、总电阻都体现了等效替换的思想,结合选项分析即可。
5.一轻弹簧挂20N的重物时,轻弹簧的总长为12cm;挂50N的重物时轻弹簧的总长为15cm。(轻弹簧始终在弹性限度内)则轻弹簧的原长是(??
)
A.?8cm???????????????????????????????????B.?10cm???????????????????????????????????C.?12cm???????????????????????????????????D.?14cm
【答案】
B
【解析】设原长为
,根据胡克定律
代入数据,整理得
故答案为:B。
【分析】已知弹簧测劲度系数和弹力大小,利用胡克定律求解弹簧的形变量。
6.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1;改用大小为F2的力拉弹簧,平衡时长度为l2。弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为(??
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
【答案】
D
【解析】由胡克定律得F=kx,式中x为形变量,设弹簧原长为l0
,
则有F1=k(l0-l1)
F2=k(l2-l0)
联立方程组可以解得
故答案为:D。
【分析】弹簧在发生弹性形变时,弹簧的弹力F和弹簧的伸长量(或压缩量)x成正比,即F=
kx
,k是物质的弹性系数。
7.如图所示的装置中,劲度系数相同的弹簧的原长相等,小球的质量均相同,弹簧和细线的质量均不计,一切摩擦忽略不计。平衡时各弹簧的长度分别为
,其大小关系是(?
?)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
【答案】
A
【解析】由于小球的质量相等,故三种情况下小球对弹簧产生的拉力相等。由胡克定律
可知,各弹簧的形变量相等,由于原长相等,故平衡时各弹簧的长度都相等,A符合题意。
故答案为:A
【分析】分别对两个小球进行受力分析,在重力和弹力的作用下,两个物体处于平衡状态,合力为零,根据该条件列方程分析求解即可。
8.如图所示,轻弹簧的两端各受
拉力作用,弹簧平衡时伸长了
(在弹性限度内),那么下列说法中正确的是(??
)
A.?弹簧的弹力为0
B.?弹簧的劲度系数k为
C.?弹簧的劲度系数k为
D.?根据公式,弹簧的劲度系数k会随弹簧弹力F的增大而增大
【答案】
C
【解析】ABC.弹簧两端同时各受10N拉力时,对其中一端受力分析,由平衡条件可知,弹簧的弹力为10N,根据胡克定律F=kx得弹簧的劲度系数为
AB不符合题意,C符合题意。
D.弹簧的劲度系数k与弹簧弹力F的变化无关,由弹簧本身性质决定,D不符合题意。
故答案为:C。
【分析】由于弹簧受到拉力后平衡,利用拉力的大小可以求出弹簧弹力的大小,利用拉力的大小结合胡克定律可以求出劲度系数的大小。
第1节重力与弹力第2课时
【素养目标】
1.了解形变、弹性形变、弹性限度等概念.
2.知道弹力产生的原因和条件
3.知道压力、支持力和绳的拉力都是弹力,会分析弹力的方向
4.理解胡克定律,并能解决有关问题
【必备知识】
知识点一、形变
1.形变
(1)形变:物体在力的作用下形状或体积的变化.
(2)弹性形变:物体形变后撤去作用力时能够恢复原状的形变.
(3)弹性限度
当形变超过一定限度时,撤去作用力后物体不能完全恢复原来的形状,这个限度叫弹性限度.
知识点二、弹力
(1)定义:发生形变的物体,由于要恢复原状,对与它接触的物体产生的力.
(2)方向
①压力和支持力的方向垂直于物体的接触面.
②绳的拉力沿着绳而指向绳收缩的方向.
弹力的方向
类型
方向
图示
接触方式
面与面
垂直公共接触面指向被支持物体
点与面
过点垂直于面指向被支持物体
点与点
垂直于公共切面指向受力物体且力的作用线一定过球(圆)心
轻绳
沿绳收缩方向
轻杆
可沿杆
伸长方向 收缩方向
可不沿杆
轻弹簧
沿弹簧形变的反方向
收缩方向 伸长方向
知识点三、胡克定律
1.胡克定律的内容
弹簧发生弹性形变时,弹力的大小F跟弹簧伸长(或缩短)的长度x成正比.
2.公式
F=kx,其中k为弹簧的劲度系数,单位为牛顿每米,符号N/m,它的大小反映了弹簧的软硬程度.
3.对胡克定律的理解
(1)弹簧发生形变时必须在弹性限度内.
(2)x是弹簧的形变量,不是弹簧形变后的实际长度.
(3)F?x图象为一条经过原点的倾斜直线,如图所示,图象斜率表示弹簧的劲度系数,对于同一根弹簧来说,劲度系数是不变的.
(4)由于F1=kx1,F2=kx2,故ΔF=F2-F1=kx2-kx1=kΔx.因此,弹簧弹力的变化量ΔF与形变量的变化量也成正比关系.
知识点四、实验:探究弹簧弹力与形变量的关系
实验思路:通过改变弹簧下端的钩码数量,控制弹簧产生的弹力,用刻度尺测量弹簧的形变量,由此探究弹簧弹力和形变量的定量关系
实验过程
将弹簧的一端固定在铁架台的横杆上,让其自由下垂,用刻度尺测出弹簧自然状态的长度,即原长。
将钩码悬挂在弹簧的下端,平衡时测量弹簧的总长度,并计算钩码受到的重力,弹簧的弹力等于钩码的重力。
改变所挂钩码的个数,重复实验过程多次
数据分析
以弹力F为纵轴,以弹力的伸长量x(x=)为横轴,用描点法作图,得出弹力F随弹簧伸长量x变化的图线。
另一种图像
若作F-L图像(L为弹簧总长),由F=kx=k()知,图像的斜率表示劲数系数k,横轴截距表示弹簧原长
【课堂检测】
1.如图所示,重为2N的物体悬挂在弹簧的下端,静止时弹簧伸长了4cm。现换用另一物体悬挂在弹簧的下端,静止时弹簧伸长了6cm(形变仍在弹性限度内),则弹簧的劲度系数和第二种情况下弹力的大小分别是(??
)
A.?50N/m,3N??????????????????B.?100N/m,6N??????????????????C.?50N/m,6N??????????????????D.?100N/m,3N
【答案】
A
【解析】重为2N的物体悬挂在弹簧的下端时,根据物体平衡条件可知,弹簧的弹力F=2N,弹簧伸长的长度x=4cm=4×10?2m。根据胡克定律F=kx
得,
。当弹簧伸长了
时,弹簧的弹力
。
故答案为:A。
【分析】利用物体的平衡方程可以求出弹簧劲度系数的大小;结合弹簧的伸长量及劲度系数的大小可以求出弹簧的弹力大小。
2.如图所示的装置中,A、B两物块的质量分别是
、
,弹簧和绳的质量均不计,绳与滑轮间的摩擦不计,重力加速度
,则下列说法正确的是(??
)
A.?固定物块A,物块B处于静止状态时,弹簧的弹力大小为20N
B.?固定物块B,物块A处于静止状态时,弹簧的弹力大小为30N
C.?先固定物块A,待A,B均静止时再释放A,释放的瞬间弹簧的弹力大小为10N
D.?物块A,B和弹簧一起稳定运动的过程中,弹簧的弹力大小为15N
【答案】
C
【解析】A.固定物块A,B处于平衡状态,根据平衡条件,可知弹簧的弹力大小等于B的重力大小,为10N,A不符合题意;
B.固定物块B,A处于平衡状态,根据平衡条件,可知弹簧的弹力大小等于A的重力大小,为20N,B不符合题意;
C.先固定物块A,由B项分析,可知弹簧的弹力大小为10N,在释放物块A的一瞬间,弹簧的弹力大小不变,仍为10N,C符合题意;
D.物块A、B和弹簧一起稳定运动的过程中,根据牛顿第二定律,对A有:
对B有:
联立解得弹簧的弹力大小
N,D不符合题意。
故答案为:C。
【分析】当绳子剪断后,其中一侧的拉力瞬间消失,但是由于弹簧来不及被压缩,故弹力不变。
【素养作业】
1.东汉时期《考工记·弓人》中记载“假令弓力胜三石,引之中三尺,弛其弦,以绳缓擐之,每加物一石,则张一尺”这表明,在弹性限度内(??
)
A.?弓的弹力与弓的形变量成正比?????????????????????????????B.?弓的弹力与弓的形变量成反比
C.?弓的弹力与弓的形变量的平方成正比??????????????????D.?弓的弹力与弓的形变量的平方成反比
【答案】
A
【解析】根据题意可知:每加物一石,则张一尺,说明每增加一石物体的重力,则形变量改变一尺,故说明在弹性限度内,弓的弹力与弓的形变量成正比,BCD不符合题意,A符合题意。
故答案为:A。
【分析】弹性体在发生弹性形变时,弹性体的弹力F和弹簧的伸长量(或压缩量)x成正比,即F=
kx
,k是物质的弹性系数。
2.某弹簧的劲度系数k=5×103N/m,在弹性限度内,当它伸长2.5cm时,产生的弹力是(?
)
A.?125N????????????????????????????????????B.?50N????????????????????????????????????C.?5N????????????????????????????????????D.?12.5N
【答案】
A
【解析】根据胡克定律:
,A符合题意,BCD不符合题意。
故答案为:A
【分析】结合弹簧的进度系数和形变量,利用胡克定律求解弹力。
3.如图所示,一根劲度系数为k的轻弹簧原长为x0,下端挂上钩码后长度为x1,则弹簧弹力的大小为(??
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
【答案】
D
【解析】由胡克定律F=kx可知,弹簧的弹力F=k(x1-x0),
故答案为:D.
【分析】本题考查胡克定律公式的应用,解题时一定要明确公式中的x为弹簧的形变量,不是原长.
4.图所示,在一张大桌子上放两个平面镜N和M,让一束光依次被两面镜子反射,最后射到墙上,形成一个光点P。用力压桌面时观察墙上光点位置的变化。下列说法中正确的是(??
)
A.?装置中平面镜的作用是通过光的反射把桌面形变放大,便于观察
B.?力F越小,光点P下移越多
C.?力F越小,光点P上移越多
D.?桌面受到的压力,是由于桌面的形变产生的
【答案】
A
【解析】A.
力的作用效果之一就是会使物体发生形变,但硬度越大的物体,其形变越不容易被觉察,为了证实硬度再大的物体在力的作用下也是有发生形变,可采用上图所示的装置进行验证。该装置是一种显示微小形变的装置,它可以把微小形变“放大”到直接看出来,A符合题意;
BC.
若在两镜之间桌面用力F下压,M、N将向中间倾斜,增大压力,则光束的入射角减小,由光的反射定律可知,光点会在刻度尺上从P点向下移动其力越大,移动越明显,力F越小,光点P下移越小。B不符合题意,C不符合题意;
D.
桌面受到的压力,是由施力物体发生形变产生的,而桌面是受力物体,D不符合题意;
故答案为:A。
【分析】物理学中用到的试验方法有很多,质点和点电荷是同一种思想方法,加速度、电场强度、电势都是采取比值法定义的物理量,重心、合力和分力、总电阻都体现了等效替换的思想,结合选项分析即可。
5.一轻弹簧挂20N的重物时,轻弹簧的总长为12cm;挂50N的重物时轻弹簧的总长为15cm。(轻弹簧始终在弹性限度内)则轻弹簧的原长是(??
)
A.?8cm???????????????????????????????????B.?10cm???????????????????????????????????C.?12cm???????????????????????????????????D.?14cm
【答案】
B
【解析】设原长为
,根据胡克定律
代入数据,整理得
故答案为:B。
【分析】已知弹簧测劲度系数和弹力大小,利用胡克定律求解弹簧的形变量。
6.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1;改用大小为F2的力拉弹簧,平衡时长度为l2。弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为(??
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
【答案】
D
【解析】由胡克定律得F=kx,式中x为形变量,设弹簧原长为l0
,
则有F1=k(l0-l1)
F2=k(l2-l0)
联立方程组可以解得
故答案为:D。
【分析】弹簧在发生弹性形变时,弹簧的弹力F和弹簧的伸长量(或压缩量)x成正比,即F=
kx
,k是物质的弹性系数。
7.如图所示的装置中,劲度系数相同的弹簧的原长相等,小球的质量均相同,弹簧和细线的质量均不计,一切摩擦忽略不计。平衡时各弹簧的长度分别为
,其大小关系是(?
?)
A.????????????????????????B.????????????????????????C.????????????????????????D.?
【答案】
A
【解析】由于小球的质量相等,故三种情况下小球对弹簧产生的拉力相等。由胡克定律
可知,各弹簧的形变量相等,由于原长相等,故平衡时各弹簧的长度都相等,A符合题意。
故答案为:A
【分析】分别对两个小球进行受力分析,在重力和弹力的作用下,两个物体处于平衡状态,合力为零,根据该条件列方程分析求解即可。
8.如图所示,轻弹簧的两端各受
拉力作用,弹簧平衡时伸长了
(在弹性限度内),那么下列说法中正确的是(??
)
A.?弹簧的弹力为0
B.?弹簧的劲度系数k为
C.?弹簧的劲度系数k为
D.?根据公式,弹簧的劲度系数k会随弹簧弹力F的增大而增大
【答案】
C
【解析】ABC.弹簧两端同时各受10N拉力时,对其中一端受力分析,由平衡条件可知,弹簧的弹力为10N,根据胡克定律F=kx得弹簧的劲度系数为
AB不符合题意,C符合题意。
D.弹簧的劲度系数k与弹簧弹力F的变化无关,由弹簧本身性质决定,D不符合题意。
故答案为:C。
【分析】由于弹簧受到拉力后平衡,利用拉力的大小可以求出弹簧弹力的大小,利用拉力的大小结合胡克定律可以求出劲度系数的大小。
