6.2.1排列-6.2.2排列数 教学课件-2020-2021学年高二数学人教A版(2019)选择性必修第三册(31张PPT)
文档属性
| 名称 | 6.2.1排列-6.2.2排列数 教学课件-2020-2021学年高二数学人教A版(2019)选择性必修第三册(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 495.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 18:24:57 | ||
图片预览











文档简介
6.2.1排列 + 6.2.2排列数
第六章 计数原理
学习目标
1.理解排列、排列数的概念.
2.能利用计数原理推导排列数公式,并掌握排列数公式及其变形,能运用排列数公式熟练地进行相关计算.
3.能熟练地运用排列知识解决一些有关排列的实际问题.
4.通过实例,体验数学知识的形成与发展,学会分析问题、解决问题的方式,培养解决实际问题的能力.
我们发现,用分步乘法计数原理解决问题时,因做了一些重复性工作而显得烦琐. 能否对这类计数问题给出一种简捷的方法呢?为此,先来分析两个具体的问题.
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
这6种不同的选法如图所示.
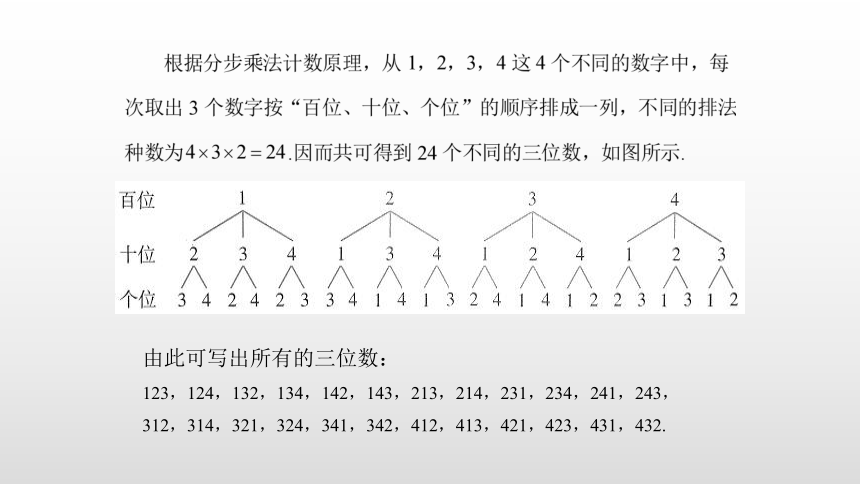
问题2 从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
显然,从4个数字中,每次取出3个,按“百位、十位、个位”的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.可以分三个步骤来解决这个问题:
第1步,确定百位上的数字,从1,2,3,4这4个数字中任取1个,有4种方法;
第2步,确定十位上的数字,当百位上的数字确定后,十位上的数字只能从余下的3个数字中去取,有3种方法;
第3步,确定个位上的数字,当百位、十位上的数字确定后,个位的数字只能从余下的2个数字中去取,有2种方法.
由此可写出所有的三位数:
123,124,132,134,142,143,213,214,231,234,241,243,312,314,321,324,341,342,412,413,421,423,431,432.
上述问题1,2的共同特点是什么?你能将它们推广到一般情形吗?
思考?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
排列
根据排列的定义,两个排列相同的充要条件是:两个排列的元素完全相同,且元素的排列顺序也相同.
排列数
排列数公式
全排列
课堂小练
课堂小结
——你学到了那些新知识呢?
本节课学习了排列、排列数的概念、排列数公式的计算及其应用.
谢谢观看!
第六章 计数原理
学习目标
1.理解排列、排列数的概念.
2.能利用计数原理推导排列数公式,并掌握排列数公式及其变形,能运用排列数公式熟练地进行相关计算.
3.能熟练地运用排列知识解决一些有关排列的实际问题.
4.通过实例,体验数学知识的形成与发展,学会分析问题、解决问题的方式,培养解决实际问题的能力.
我们发现,用分步乘法计数原理解决问题时,因做了一些重复性工作而显得烦琐. 能否对这类计数问题给出一种简捷的方法呢?为此,先来分析两个具体的问题.
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
这6种不同的选法如图所示.
问题2 从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
显然,从4个数字中,每次取出3个,按“百位、十位、个位”的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.可以分三个步骤来解决这个问题:
第1步,确定百位上的数字,从1,2,3,4这4个数字中任取1个,有4种方法;
第2步,确定十位上的数字,当百位上的数字确定后,十位上的数字只能从余下的3个数字中去取,有3种方法;
第3步,确定个位上的数字,当百位、十位上的数字确定后,个位的数字只能从余下的2个数字中去取,有2种方法.
由此可写出所有的三位数:
123,124,132,134,142,143,213,214,231,234,241,243,312,314,321,324,341,342,412,413,421,423,431,432.
上述问题1,2的共同特点是什么?你能将它们推广到一般情形吗?
思考?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
排列
根据排列的定义,两个排列相同的充要条件是:两个排列的元素完全相同,且元素的排列顺序也相同.
排列数
排列数公式
全排列
课堂小练
课堂小结
——你学到了那些新知识呢?
本节课学习了排列、排列数的概念、排列数公式的计算及其应用.
谢谢观看!
