北师大版2021-2022学年七年级数学上册3.1 字母表示数课件(共48张PPT)
文档属性
| 名称 | 北师大版2021-2022学年七年级数学上册3.1 字母表示数课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 815.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览





文档简介
3.1 字母表示数
北师大版 · 数学· 七年级(上)
第三章 整式及其加减
1.能用字母表示以前学过的运算律和计算公式。
2.体会字母表示数的意义,形成初步的符号感。
3.经历实际操作、独立思考、沟通交流的过程,感受从具体到抽象的思想。
学习目标
练习(唱不完的儿歌)
1只青蛙1张嘴,2只眼睛4条腿,1声扑通跳下水;
2只青蛙2张嘴,4只眼睛8条腿,2声扑通跳下水;
3只青蛙3张嘴,6只眼睛12条腿,3声扑通跳下水;
…………
n只青蛙呢?
n只青蛙n张嘴,
2n只眼睛4n条腿,
n声扑通跳下水.
导入新知
十只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
……
a只青蛙_____张嘴,___只眼睛____条腿,_______声扑通跳下水.
a
a
10
20
40
10
100
200
400
100
4a
2a
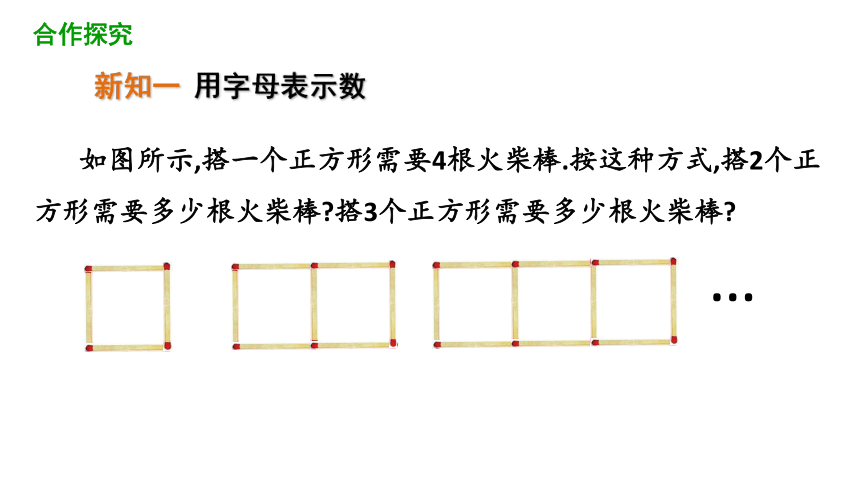
如图所示,搭一个正方形需要4根火柴棒.按这种方式,搭2个正方形需要多少根火柴棒?搭3个正方形需要多少根火柴棒?
新知一 用字母表示数
…
合作探究
(1)按上面的方式,搭2个正方形需要____根火柴棒,搭3个正方形需要____根火柴棒.
(2) 搭7个这样的正方形需要_____根火柴棒.
7
10
22
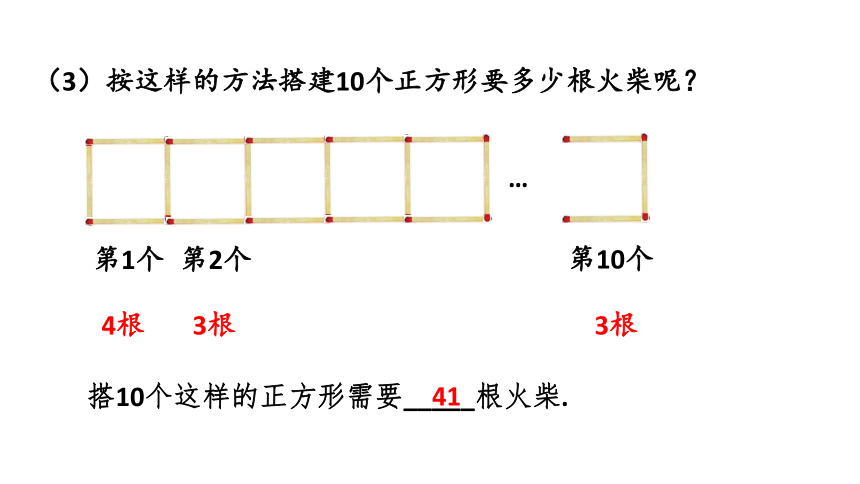
(3)按这样的方法搭建10个正方形要多少根火柴呢?
第1个
4根
第2个
第10个
3根
3根
…
搭10个这样的正方形需要_____根火柴.
41
……
……
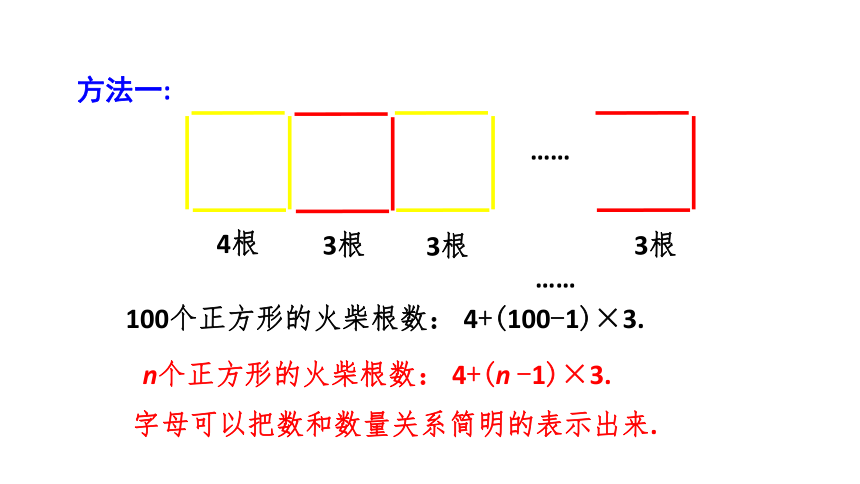
100个正方形的火柴根数: 4+(100-1)×3.
方法一:
n个正方形的火柴根数: 4+(n -1)×3.
字母可以把数和数量关系简明的表示出来.
4根
3根
3根
3根
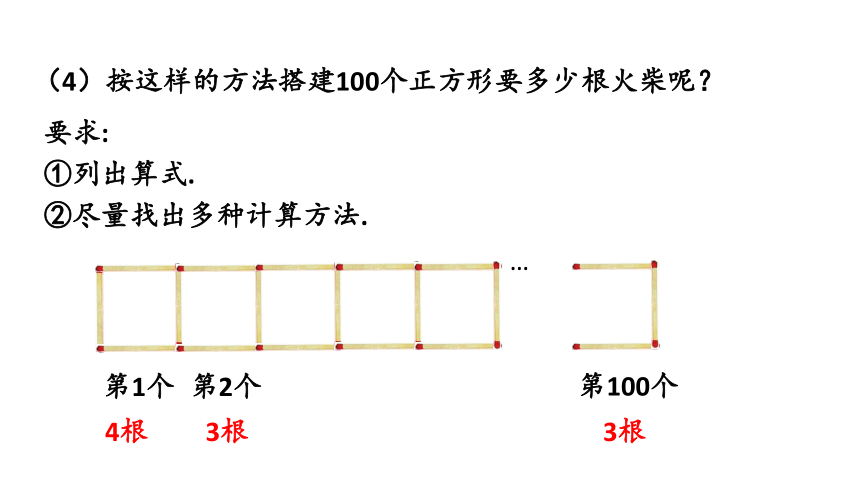
(4)按这样的方法搭建100个正方形要多少根火柴呢?
要求:
①列出算式.
②尽量找出多种计算方法.
第1个
4根
第2个
第100个
3根
3根
…
……
……
100个正方形的火柴根数: 1+3×100.
方法二:
n个正方形的火柴根数: 1+3n.
1根
3根
3根
3根
3根
1根
……
1根
1根
1根
1根
1根
1根
1根
多1根
方法三:
100个正方形的火柴根数: 100+100+(100+1).
n个正方形的火柴根数: n + n +( n+1).
……
4根
4根
4根
4根
少1根
少1根
少1根
100个正方形的火柴根数: 4×100-(100-1).
方法四:
n个正方形的火柴根数: 4n-( n-1).
(5) 按这样的方法搭建2019个正方形要多少根火柴呢?
①4+(n -1)×3
②1+3n
③n + n +( n +1)
④4n-( n-1)
只要把2019代上面任何一式都行
字母可表示任何数,即可表示正数,又可表示负数,也可表示0.
典例精析 用字母表示数
方法点拨:用字母表示数时,若式子是积商的形式,则单位名称写在式子的后面即可;若式子是和或差的形式,则应把整个式子用括号括起来,再将单位名称写在后面.
例 小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为_______米/秒.
3v
3
6
9
12
15
30
100
(2)摆第n个图案需要多少枚棋子?
解:摆第n个图案需要3n枚棋子.
用棋子摆成下列一组图案:
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 图案编号
①
②
③
④
⑤
⑩
火柴棒根数
?
?
?
?
?
?
?
巩固新知
新知二 用字母表示运算律、公式等数学问题
你能否举出一些字母表示数和数量关系的例子?
在上面的活动中,我们借助字母描述了正方形的个数和火柴棒的根数之间的关系.
合作探究
a
a
a
b
a
h
a
h
a
h
b
S = a2
S = ab
S = ah
S = ah÷2
S =(a + b)h÷2
用字母表示面积公式
运算定律
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b)+c = a +(b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac+bc
用字母表示数的运算律
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
字母表示数注意事项
100×t
100t
nm
mn
nn
n2
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
1n
n
n÷3
字母表示数注意事项
????????
?
1????????n
?
????????????
?
判断下列式子书写是否规范,不规范的请改正.
????????????ab
?
xy
-n
3x
????????
?
x×y
2????????ab
?
-1n
x3
m÷3
典例精析 用字母表示数在实际中的应用
方法点拨:用字母表示数,可以把数和数量关系简明地表示出来,给我们研究问题带来很大方便.
解:图中阴影部分的面积为
用字母表示图中阴影部分的面积?
R2- ???????????????? .
?
某商品打七折后的价格为a元,则原价为( )
B
A .a元 B.????????????a元
C.30%a元 D.????????????a元
?
巩固新知
1.若苹果每千克m元,则2千克苹果共( )
A.(m-2)元 B.(m+2)元
C. 元 D.2m元
D
课堂练习
2.苹果原价是每斤a元,现在按八折出售,假如现在要买一斤,那么需要付费( )
A.0.8a元 B.0.2a元
C.1.8a元 D.(a+0.8)元
A
3.七年级(1)班男生有a人,女生人数比男生人数的一半多4人,则女生人数是( )
A. ???????? (a+4) B.????????(a-4)
C. ????????a+4 D. ?????????a-4
?
C
字母表示数
字母可以表示任何数
用字母表示数的运算律和公式法则
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:ab=ba
乘法结合律:(ab) c=a (bc)
分配律:a(b +c)=ab+ac
归纳新知
1.每包书有12册,n包书有____册.
2.底边长为a,高为h的三角形的面积是____.
3.一个长方体的长、宽都是a,高为h,它的体积是____.
4.一个长方形的长是0.9,宽是a,这个长方形的面积是____.
12n
a2h
0.9a
课后练习
5.一辆汽车的速度是v千米/小时,行驶t小时所走的路程是____千米.
6.一台电视机的原价是a元,现按原价的9折出售,则这台电视机现在的售价为 .
vt
90%a
7.“早穿皮袄午穿纱”这句民谣形象地描绘了我们新疆奇妙的气温变化现象.乌鲁木齐市五月的某一天,最低气温是t ℃,温差是15 ℃,则当天的最高气温是 ℃.
8.吉林广播电视塔五一假期第一天接待游客m人,第二天接待游客n人,则这2天平均每天接待游客 人.(用含m,n的代数式表示)
(t+15)
9.买单价为a元的体温计n个,付出b元,应找回的钱数是( )
A.(b-na)元
B.(b-n)元
C.(na-b)元
D.(b-a)元
A
10.假期的一天上午,小明看一本课外书,他从第m页开始看到第n页结束(n>m),他这天上午看的书共有( )
A.(m+n)页
B.(n-m)页
C.(n-m-1)页
D.(n-m+1)页
D
B
C
13.有一个两位数,它的十位数字是a,个位数字是b,则这个两位数是( )
A.a+b
B.a×b
C.10a+b
D.10(a+b)
C
14.某地出租车的收费标准是:3千米以内(包括3千米)为起步价收5元,3千米以后每千米价为1.5元.
(1)若某人乘坐了1.5千米,则应收费____元;
(2)若某人乘坐了6千米,则应收费____元;
(3)若某人乘坐了x千米(x>3)的路程,则应收费 元.(只列式,不计算)
5
9.5
[1.5(x-3)+5]
15.(2019·宁波改编)下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案○,n)需 根火柴棒.
(7n+1)
16.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元.
则代数式500-3a-2b表示的意义为 .
体育委员买了3个足球和2个篮球后剩余的经费
17.用字母表示图中阴影部分的面积.(不计算结果)
B
19.张老板以每颗a元的单价买进水蜜桃100颗,现以每颗比单价多20%的价格卖出80颗后,再以每颗比单价低b元的价格将剩下的20颗卖出,则全部水蜜桃共卖( )
A.[80a+20(a-b)]元
B.[80(1+20%)a+20b]元
C.[100(1+20%)a-20(a-b)]元
D.[80(1+20%)a+20(a-b)]元
D
20.某商店进了一批油,出售时要在进价的基础上加一定的利润,其数量a与售价c的关系如下表:
下列用数量a表示售价c的式子中,正确的是( )
A.c=10a+0.2 B.c=10+0.2a
C.c=(10+0.2)a D.c=10+0.2+a
C
21.(2019·大庆)如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第n个图形中共有三角形的个数为 个.
(4n-3)
24.用棋子摆出下列一组图形:
(1)填写下表:
图形编号
1
2
3
4
5
6
图形中的棋子
6
9
12
15
18
21
(2)照这样的方式摆下去,写出第n个图形棋子的枚数;(用含n的代数式表示)
(3)如果某一个图形共有99枚棋子,你知道它是第几个图形吗?
解:(2)3n+3 (3)由题意得3n+3=99,解得n=32,所以它是第32个图形
25.张老师到体育用品专卖店为学校购买排球,排球单价为a元,买10个以上按7折优惠,用代数式表示:
(1)购买30个排球应付多少钱?
(2)购买b个排球应付多少钱?
解:(1)21a元 (2)分两种情况:当0<b≤10且为整数时,购买b个排球应付ab元;当b>10且为整数时,购买b个排球应付0.7ab元
再
见
北师大版 · 数学· 七年级(上)
第三章 整式及其加减
1.能用字母表示以前学过的运算律和计算公式。
2.体会字母表示数的意义,形成初步的符号感。
3.经历实际操作、独立思考、沟通交流的过程,感受从具体到抽象的思想。
学习目标
练习(唱不完的儿歌)
1只青蛙1张嘴,2只眼睛4条腿,1声扑通跳下水;
2只青蛙2张嘴,4只眼睛8条腿,2声扑通跳下水;
3只青蛙3张嘴,6只眼睛12条腿,3声扑通跳下水;
…………
n只青蛙呢?
n只青蛙n张嘴,
2n只眼睛4n条腿,
n声扑通跳下水.
导入新知
十只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
……
a只青蛙_____张嘴,___只眼睛____条腿,_______声扑通跳下水.
a
a
10
20
40
10
100
200
400
100
4a
2a
如图所示,搭一个正方形需要4根火柴棒.按这种方式,搭2个正方形需要多少根火柴棒?搭3个正方形需要多少根火柴棒?
新知一 用字母表示数
…
合作探究
(1)按上面的方式,搭2个正方形需要____根火柴棒,搭3个正方形需要____根火柴棒.
(2) 搭7个这样的正方形需要_____根火柴棒.
7
10
22
(3)按这样的方法搭建10个正方形要多少根火柴呢?
第1个
4根
第2个
第10个
3根
3根
…
搭10个这样的正方形需要_____根火柴.
41
……
……
100个正方形的火柴根数: 4+(100-1)×3.
方法一:
n个正方形的火柴根数: 4+(n -1)×3.
字母可以把数和数量关系简明的表示出来.
4根
3根
3根
3根
(4)按这样的方法搭建100个正方形要多少根火柴呢?
要求:
①列出算式.
②尽量找出多种计算方法.
第1个
4根
第2个
第100个
3根
3根
…
……
……
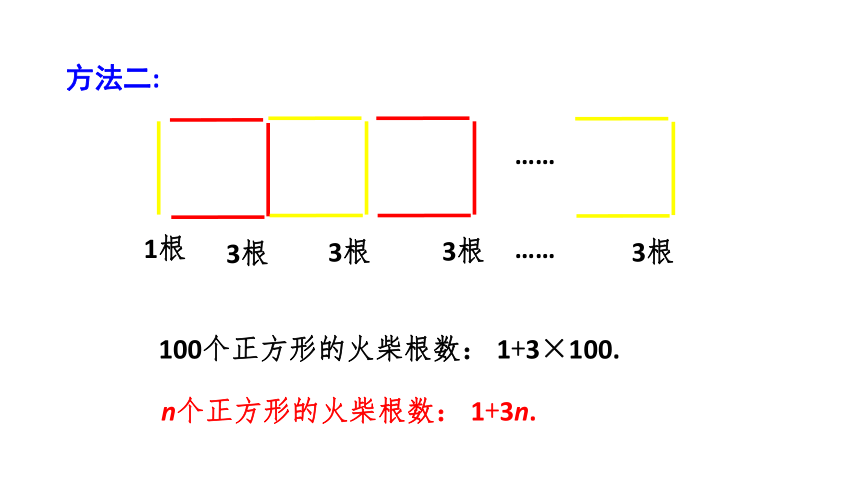
100个正方形的火柴根数: 1+3×100.
方法二:
n个正方形的火柴根数: 1+3n.
1根
3根
3根
3根
3根
1根
……
1根
1根
1根
1根
1根
1根
1根
多1根
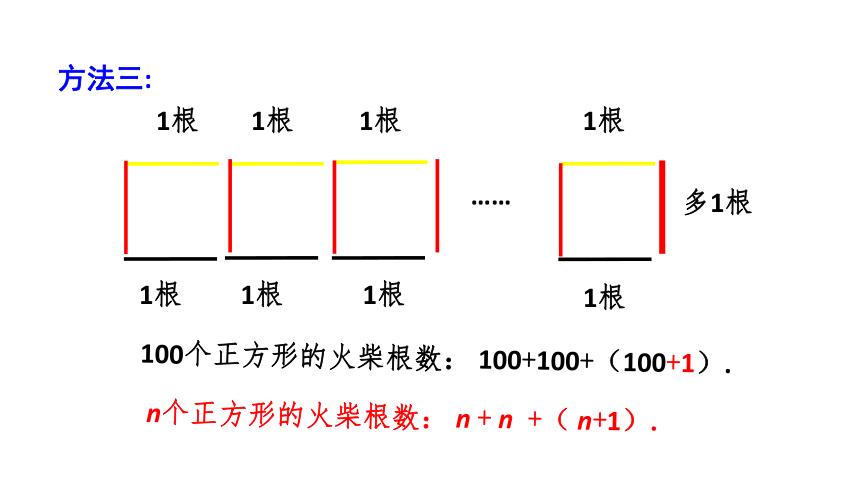
方法三:
100个正方形的火柴根数: 100+100+(100+1).
n个正方形的火柴根数: n + n +( n+1).
……
4根
4根
4根
4根
少1根
少1根
少1根
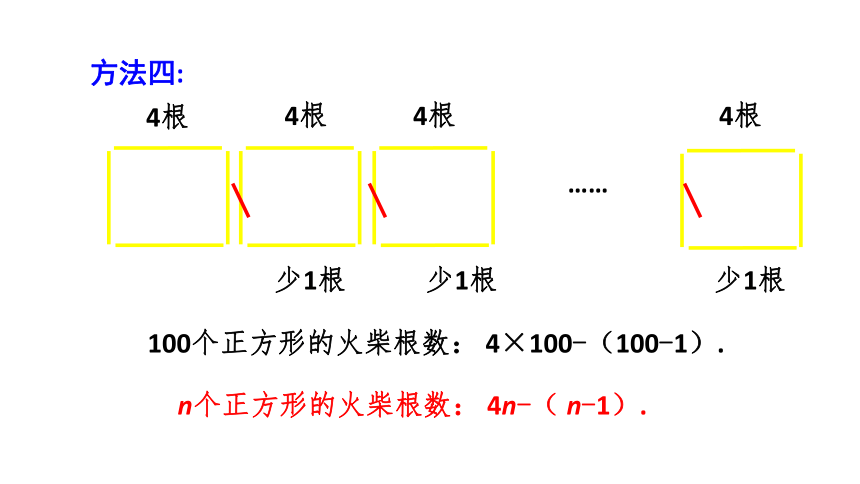
100个正方形的火柴根数: 4×100-(100-1).
方法四:
n个正方形的火柴根数: 4n-( n-1).
(5) 按这样的方法搭建2019个正方形要多少根火柴呢?
①4+(n -1)×3
②1+3n
③n + n +( n +1)
④4n-( n-1)
只要把2019代上面任何一式都行
字母可表示任何数,即可表示正数,又可表示负数,也可表示0.
典例精析 用字母表示数
方法点拨:用字母表示数时,若式子是积商的形式,则单位名称写在式子的后面即可;若式子是和或差的形式,则应把整个式子用括号括起来,再将单位名称写在后面.
例 小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为_______米/秒.
3v
3
6
9
12
15
30
100
(2)摆第n个图案需要多少枚棋子?
解:摆第n个图案需要3n枚棋子.
用棋子摆成下列一组图案:
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 图案编号
①
②
③
④
⑤
⑩
火柴棒根数
?
?
?
?
?
?
?
巩固新知
新知二 用字母表示运算律、公式等数学问题
你能否举出一些字母表示数和数量关系的例子?
在上面的活动中,我们借助字母描述了正方形的个数和火柴棒的根数之间的关系.
合作探究
a
a
a
b
a
h
a
h
a
h
b
S = a2
S = ab
S = ah
S = ah÷2
S =(a + b)h÷2
用字母表示面积公式
运算定律
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b)+c = a +(b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac+bc
用字母表示数的运算律
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
字母表示数注意事项
100×t
100t
nm
mn
nn
n2
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
1n
n
n÷3
字母表示数注意事项
????????
?
1????????n
?
????????????
?
判断下列式子书写是否规范,不规范的请改正.
????????????ab
?
xy
-n
3x
????????
?
x×y
2????????ab
?
-1n
x3
m÷3
典例精析 用字母表示数在实际中的应用
方法点拨:用字母表示数,可以把数和数量关系简明地表示出来,给我们研究问题带来很大方便.
解:图中阴影部分的面积为
用字母表示图中阴影部分的面积?
R2- ???????????????? .
?
某商品打七折后的价格为a元,则原价为( )
B
A .a元 B.????????????a元
C.30%a元 D.????????????a元
?
巩固新知
1.若苹果每千克m元,则2千克苹果共( )
A.(m-2)元 B.(m+2)元
C. 元 D.2m元
D
课堂练习
2.苹果原价是每斤a元,现在按八折出售,假如现在要买一斤,那么需要付费( )
A.0.8a元 B.0.2a元
C.1.8a元 D.(a+0.8)元
A
3.七年级(1)班男生有a人,女生人数比男生人数的一半多4人,则女生人数是( )
A. ???????? (a+4) B.????????(a-4)
C. ????????a+4 D. ?????????a-4
?
C
字母表示数
字母可以表示任何数
用字母表示数的运算律和公式法则
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:ab=ba
乘法结合律:(ab) c=a (bc)
分配律:a(b +c)=ab+ac
归纳新知
1.每包书有12册,n包书有____册.
2.底边长为a,高为h的三角形的面积是____.
3.一个长方体的长、宽都是a,高为h,它的体积是____.
4.一个长方形的长是0.9,宽是a,这个长方形的面积是____.
12n
a2h
0.9a
课后练习
5.一辆汽车的速度是v千米/小时,行驶t小时所走的路程是____千米.
6.一台电视机的原价是a元,现按原价的9折出售,则这台电视机现在的售价为 .
vt
90%a
7.“早穿皮袄午穿纱”这句民谣形象地描绘了我们新疆奇妙的气温变化现象.乌鲁木齐市五月的某一天,最低气温是t ℃,温差是15 ℃,则当天的最高气温是 ℃.
8.吉林广播电视塔五一假期第一天接待游客m人,第二天接待游客n人,则这2天平均每天接待游客 人.(用含m,n的代数式表示)
(t+15)
9.买单价为a元的体温计n个,付出b元,应找回的钱数是( )
A.(b-na)元
B.(b-n)元
C.(na-b)元
D.(b-a)元
A
10.假期的一天上午,小明看一本课外书,他从第m页开始看到第n页结束(n>m),他这天上午看的书共有( )
A.(m+n)页
B.(n-m)页
C.(n-m-1)页
D.(n-m+1)页
D
B
C
13.有一个两位数,它的十位数字是a,个位数字是b,则这个两位数是( )
A.a+b
B.a×b
C.10a+b
D.10(a+b)
C
14.某地出租车的收费标准是:3千米以内(包括3千米)为起步价收5元,3千米以后每千米价为1.5元.
(1)若某人乘坐了1.5千米,则应收费____元;
(2)若某人乘坐了6千米,则应收费____元;
(3)若某人乘坐了x千米(x>3)的路程,则应收费 元.(只列式,不计算)
5
9.5
[1.5(x-3)+5]
15.(2019·宁波改编)下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案○,n)需 根火柴棒.
(7n+1)
16.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元.
则代数式500-3a-2b表示的意义为 .
体育委员买了3个足球和2个篮球后剩余的经费
17.用字母表示图中阴影部分的面积.(不计算结果)
B
19.张老板以每颗a元的单价买进水蜜桃100颗,现以每颗比单价多20%的价格卖出80颗后,再以每颗比单价低b元的价格将剩下的20颗卖出,则全部水蜜桃共卖( )
A.[80a+20(a-b)]元
B.[80(1+20%)a+20b]元
C.[100(1+20%)a-20(a-b)]元
D.[80(1+20%)a+20(a-b)]元
D
20.某商店进了一批油,出售时要在进价的基础上加一定的利润,其数量a与售价c的关系如下表:
下列用数量a表示售价c的式子中,正确的是( )
A.c=10a+0.2 B.c=10+0.2a
C.c=(10+0.2)a D.c=10+0.2+a
C
21.(2019·大庆)如图,①是一个三角形,分别连接这个三角形三边中点得到图②,再连接图②中间小三角形三边的中点得到图③,按这样的方法进行下去,第n个图形中共有三角形的个数为 个.
(4n-3)
24.用棋子摆出下列一组图形:
(1)填写下表:
图形编号
1
2
3
4
5
6
图形中的棋子
6
9
12
15
18
21
(2)照这样的方式摆下去,写出第n个图形棋子的枚数;(用含n的代数式表示)
(3)如果某一个图形共有99枚棋子,你知道它是第几个图形吗?
解:(2)3n+3 (3)由题意得3n+3=99,解得n=32,所以它是第32个图形
25.张老师到体育用品专卖店为学校购买排球,排球单价为a元,买10个以上按7折优惠,用代数式表示:
(1)购买30个排球应付多少钱?
(2)购买b个排球应付多少钱?
解:(1)21a元 (2)分两种情况:当0<b≤10且为整数时,购买b个排球应付ab元;当b>10且为整数时,购买b个排球应付0.7ab元
再
见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
