11.2.2 三角形的外角 课件(共25张PPT)
文档属性
| 名称 | 11.2.2 三角形的外角 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 15:44:56 | ||
图片预览






文档简介
11.2.2 三角形的外角
第十一章 三角形
2021-2022学年初中数学人教版八年级上册
1.理解并掌握三角形的外角的概念.
2.能够在能够复杂图形中找出外角.(难点)
3.掌握三角形的一个外角等于与它不相邻的两个内角
的和及三角形的内角和.(重点)
4.会利用三角形的外角性质解决问题.
学习目标
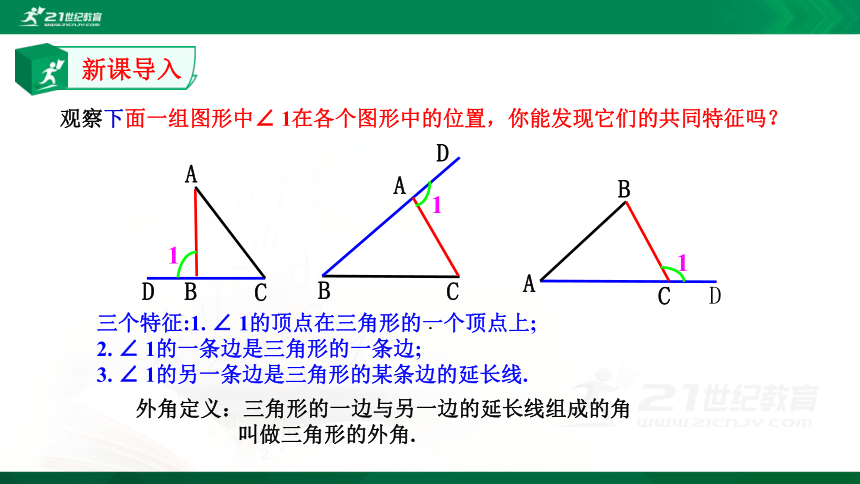
观察下面一组图形中∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
外角定义:
三角形的一边与另一边的延长线组成的角
叫做三角形的外角.
三个特征:1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线.
·
·
·
新课导入
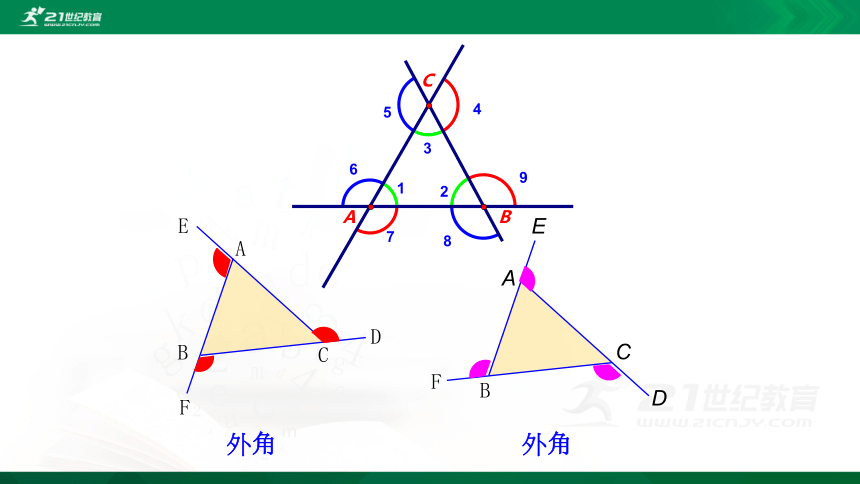
画一个三角形,再画出它所有的外角.
想一想:
1. 每一个三角形有几个外角?
2. 每一个顶点处相对应的外角有几个?
3. 这些外角中有几个外角相等?
4. 三角形的每一个外角与三角形的三个内角有什么位置关系?
探究新知
A
B
D
E
F
C
外角
A
B
D
E
F
C
外角
9
8
7
6
5
4
3
2
1
B
C
A
1. 每一个三角形都有 外角;
2. 每一个顶点相对应的外角都有
4. 一个三角形的每一个外角对应一个
和两个
3. 这6个外角中有 外角相等;
6个
2个;
3对
相邻的内角 不相邻的内角.
归纳小结
你能在下图中填出已知角是哪个三角形的外角或内角吗?
1.∠ BEF是( )的外角,也是( )
的内角.
2.∠ BDC是( )的外角,也是( )
的内角.
3.∠ BFC是( )的外角,也是( ) 的内角.
A
B
F
E
C
D
内外角是相对而言的
△AEC
△BEF、
△BEC
△ABD
△BDC
、 △CDF
△BEF、 △ CDF
△BFC
针对练习
三角形的一个外角与三角形三个内角之间有何关系?
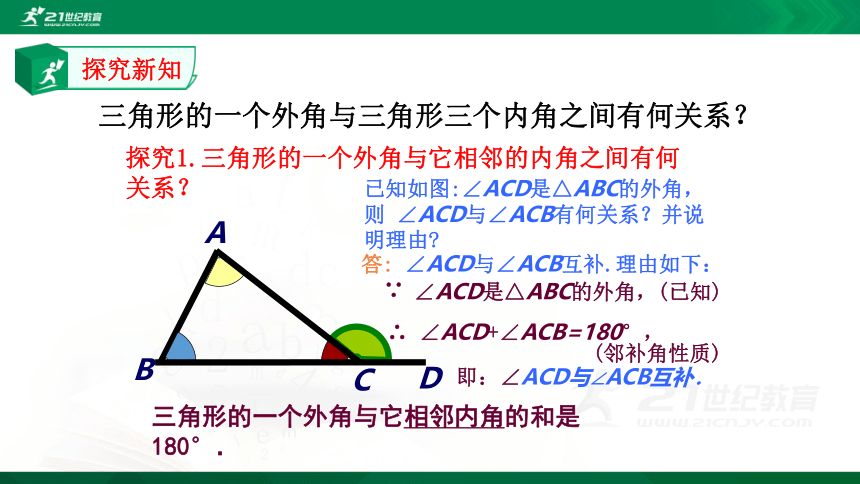
探究1.三角形的一个外角与它相邻的内角之间有何关系?
三角形的一个外角与它相邻内角的和是180°.
答: ∠ACD与∠ACB互补.理由如下:
已知如图:∠ACD是△ABC的外角,则 ∠ACD与∠ACB有何关系?并说明理由?
A
B
C
D
∵
∠ACD是△ABC的外角,(已知)
∴ ∠ACD+∠ACB=180°,
(邻补角性质)
即:∠ACD与∠ACB互补.
探究新知
探究2:三角形的一个外角与它不相邻的两个内角之间有何关系?
想一想:
在一张白纸上任意画一个三角形ABC,如图2,把∠B、∠C剪下拼在一起,放到∠CAD上,看看会出现什么结果?
A
B
C
D
图2
∠CAD=∠B+∠C.
动手长智慧
你能用推理的方法来论证∠ACD= ∠B+ ∠ A吗?你能用几种方法呢?相信你一定能行!
D
A
B
C
探究新知
D
A
B
C
∴∠ACD =180 ° -∠ACB.
∴∠A+ ∠B =180 ° -∠ACB,
∵∠ACD+ ∠ACB=180°
解:
(邻补角的定义),
又∵∠A+ ∠B+ ∠ACB=180°.
(三角形内角和180 ° )
∴∠A+ ∠B = ∠ACD.
(等量代换)
方法一:
方法二:
擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?哪位同学证明一下.
1
(CE//BA)
A
E
C
B
D
三角形的一个外角等于与它不相邻的两个内角的和.
结论
归纳小结
三角形的一个外角大于任何一个与它不相邻的内角.
∵∠ACD= ∠A+ ∠B,
∴∠ACD﹥∠A,
∠ACD﹥∠B.
D
A
C
B
探究3:三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系?
结论
探究新知
三角形外角的性质:
性质 1. 三角形的一个外角等于
与它不相邻的两个内角的和.
∠B+∠C=∠CAD.
性质 2. 三角形的一个外角大于任何一个与它不相邻的内角.
∠CAD > ∠B, ∠CAD > ∠C.
A
B
C
D
归纳小结
例1:一个零件的形状如图所示,按规定∠BAC=90°, ∠B=21°,∠C=20°,检验工人量得∠BDC=130°,就断定这个零件不合格,你能运用所学的知识说出其中的道理吗?
C
A
B
D
提示:可以先计算出合格时∠BDC的度数,但是∠BDC与∠A 、∠B、 ∠C不在同一个三角形内,因而无法找到它们之间的数量关系,因此需要添加辅助线.那如何添加辅助线才能建立这几个角之间的联系呢?
例题讲解
例2 已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的一个外角(已知),
∴ ∠1>∠3(三角形的一个外角大 于任何一个和它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义),
∴∠3>∠2(三角形的一个外角大于任何一个和它不相邻的内角),
∴ ∠1>∠2.
C
A
B
F
1
3
4
5
E
D
2
例题讲解
1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
c
2.如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°
F
E
D
C
B
A
B
课堂练习
3.如图所示,∠1=_______.
140
°
80
°
1
120 °
4.已知等腰三角形的一个外角为150°,
则它的底角为 .
30或75°
5.如图所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.
D
C
B
A
120°
6.把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?
A
B
C
D
E
F
拓广延伸
三角形的三个性质
② 三角形的一个外角等于与它不相邻的两个内角的和.
③三角形的一个外角大于任何一个与它
不相邻的内角.
①三角形的一个外角与它相邻的内角.
小 结
课堂小结
谢谢聆听
第十一章 三角形
2021-2022学年初中数学人教版八年级上册
1.理解并掌握三角形的外角的概念.
2.能够在能够复杂图形中找出外角.(难点)
3.掌握三角形的一个外角等于与它不相邻的两个内角
的和及三角形的内角和.(重点)
4.会利用三角形的外角性质解决问题.
学习目标
观察下面一组图形中∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
外角定义:
三角形的一边与另一边的延长线组成的角
叫做三角形的外角.
三个特征:1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线.
·
·
·
新课导入
画一个三角形,再画出它所有的外角.
想一想:
1. 每一个三角形有几个外角?
2. 每一个顶点处相对应的外角有几个?
3. 这些外角中有几个外角相等?
4. 三角形的每一个外角与三角形的三个内角有什么位置关系?
探究新知
A
B
D
E
F
C
外角
A
B
D
E
F
C
外角
9
8
7
6
5
4
3
2
1
B
C
A
1. 每一个三角形都有 外角;
2. 每一个顶点相对应的外角都有
4. 一个三角形的每一个外角对应一个
和两个
3. 这6个外角中有 外角相等;
6个
2个;
3对
相邻的内角 不相邻的内角.
归纳小结
你能在下图中填出已知角是哪个三角形的外角或内角吗?
1.∠ BEF是( )的外角,也是( )
的内角.
2.∠ BDC是( )的外角,也是( )
的内角.
3.∠ BFC是( )的外角,也是( ) 的内角.
A
B
F
E
C
D
内外角是相对而言的
△AEC
△BEF、
△BEC
△ABD
△BDC
、 △CDF
△BEF、 △ CDF
△BFC
针对练习
三角形的一个外角与三角形三个内角之间有何关系?
探究1.三角形的一个外角与它相邻的内角之间有何关系?
三角形的一个外角与它相邻内角的和是180°.
答: ∠ACD与∠ACB互补.理由如下:
已知如图:∠ACD是△ABC的外角,则 ∠ACD与∠ACB有何关系?并说明理由?
A
B
C
D
∵
∠ACD是△ABC的外角,(已知)
∴ ∠ACD+∠ACB=180°,
(邻补角性质)
即:∠ACD与∠ACB互补.
探究新知
探究2:三角形的一个外角与它不相邻的两个内角之间有何关系?
想一想:
在一张白纸上任意画一个三角形ABC,如图2,把∠B、∠C剪下拼在一起,放到∠CAD上,看看会出现什么结果?
A
B
C
D
图2
∠CAD=∠B+∠C.
动手长智慧
你能用推理的方法来论证∠ACD= ∠B+ ∠ A吗?你能用几种方法呢?相信你一定能行!
D
A
B
C
探究新知
D
A
B
C
∴∠ACD =180 ° -∠ACB.
∴∠A+ ∠B =180 ° -∠ACB,
∵∠ACD+ ∠ACB=180°
解:
(邻补角的定义),
又∵∠A+ ∠B+ ∠ACB=180°.
(三角形内角和180 ° )
∴∠A+ ∠B = ∠ACD.
(等量代换)
方法一:
方法二:
擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?哪位同学证明一下.
1
(CE//BA)
A
E
C
B
D
三角形的一个外角等于与它不相邻的两个内角的和.
结论
归纳小结
三角形的一个外角大于任何一个与它不相邻的内角.
∵∠ACD= ∠A+ ∠B,
∴∠ACD﹥∠A,
∠ACD﹥∠B.
D
A
C
B
探究3:三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系?
结论
探究新知
三角形外角的性质:
性质 1. 三角形的一个外角等于
与它不相邻的两个内角的和.
∠B+∠C=∠CAD.
性质 2. 三角形的一个外角大于任何一个与它不相邻的内角.
∠CAD > ∠B, ∠CAD > ∠C.
A
B
C
D
归纳小结
例1:一个零件的形状如图所示,按规定∠BAC=90°, ∠B=21°,∠C=20°,检验工人量得∠BDC=130°,就断定这个零件不合格,你能运用所学的知识说出其中的道理吗?
C
A
B
D
提示:可以先计算出合格时∠BDC的度数,但是∠BDC与∠A 、∠B、 ∠C不在同一个三角形内,因而无法找到它们之间的数量关系,因此需要添加辅助线.那如何添加辅助线才能建立这几个角之间的联系呢?
例题讲解
例2 已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的一个外角(已知),
∴ ∠1>∠3(三角形的一个外角大 于任何一个和它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义),
∴∠3>∠2(三角形的一个外角大于任何一个和它不相邻的内角),
∴ ∠1>∠2.
C
A
B
F
1
3
4
5
E
D
2
例题讲解
1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
c
2.如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°
F
E
D
C
B
A
B
课堂练习
3.如图所示,∠1=_______.
140
°
80
°
1
120 °
4.已知等腰三角形的一个外角为150°,
则它的底角为 .
30或75°
5.如图所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.
D
C
B
A
120°
6.把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?
A
B
C
D
E
F
拓广延伸
三角形的三个性质
② 三角形的一个外角等于与它不相邻的两个内角的和.
③三角形的一个外角大于任何一个与它
不相邻的内角.
①三角形的一个外角与它相邻的内角.
小 结
课堂小结
谢谢聆听
