二次函数的复习
图片预览



文档简介
(共42张PPT)
退出
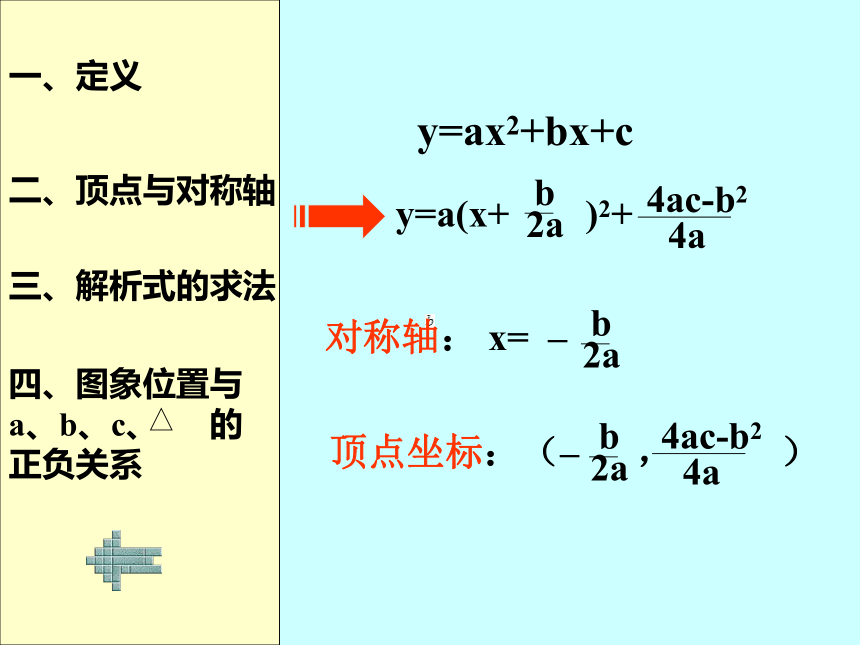
一、定义
二、顶点与对称轴
三、解析式的求法
四、图象位置与
a、b、c、 的
正负关系
一、定义
二、顶点与对称轴
四、图象位置与
a、b、c、 的
正负关系
一般地,如果
y=ax2+bx+c(a,b,c
是常数,a≠0),那么,y
叫做x的二次函数。
三、解析式的求法
一、定义
二、顶点与对称轴
三、解析式的求法
四、图象位置与
a、b、c、 的
正负关系
y=ax2+bx+c
y=a(x+ )2+
b
2a
4ac-b2
4a
对称轴: x= –
b
2a
顶点坐标:(– , )
b
2a
4ac-b2
4a
一、定义
二、顶点与对称轴
三、解析式的求法
四、图象位置与
a、b、c、 的
正负关系
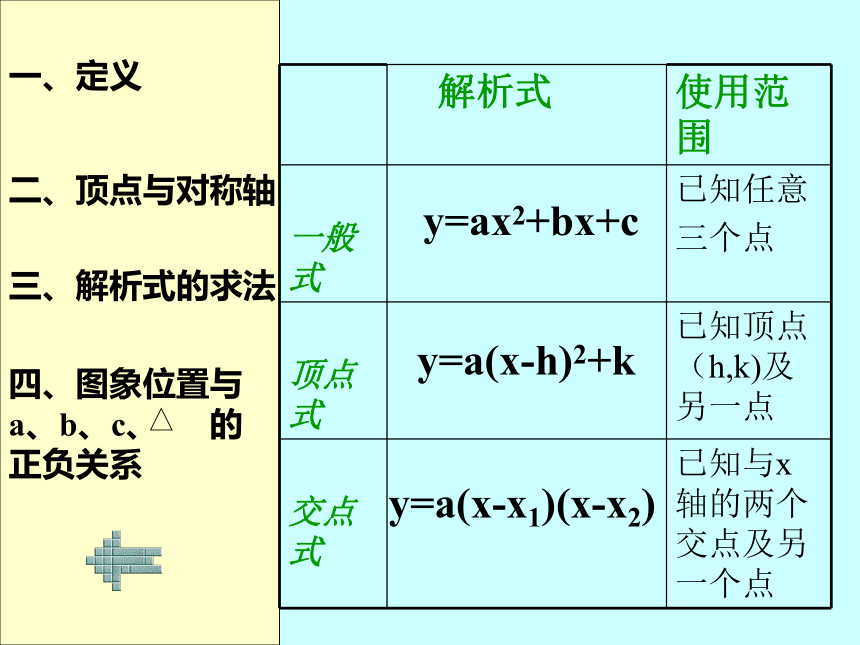
解析式 使用范围
一般式 已知任意
三个点
顶点式 已知顶点(h,k)及另一点
交点式 已知与x轴的两个交点及另一个点
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
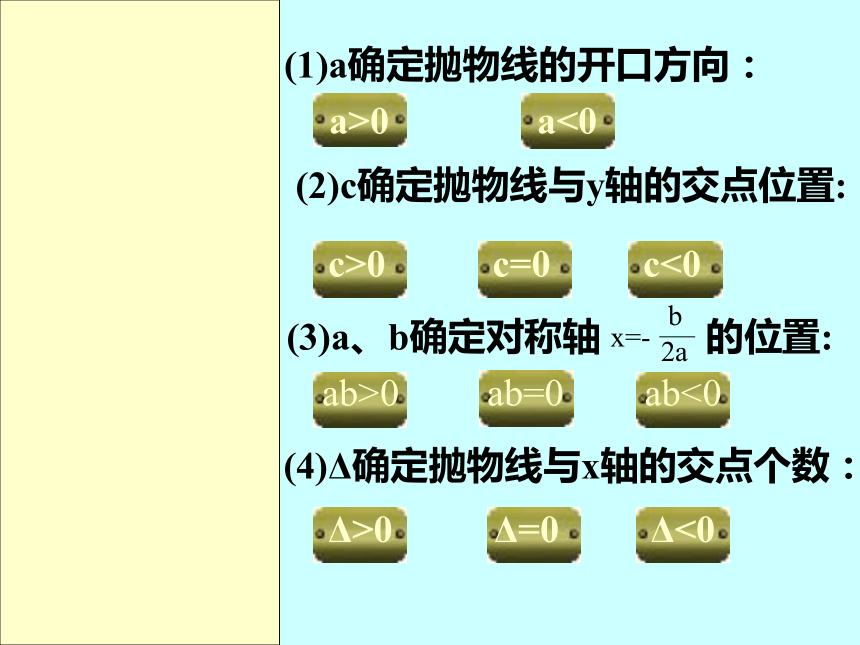
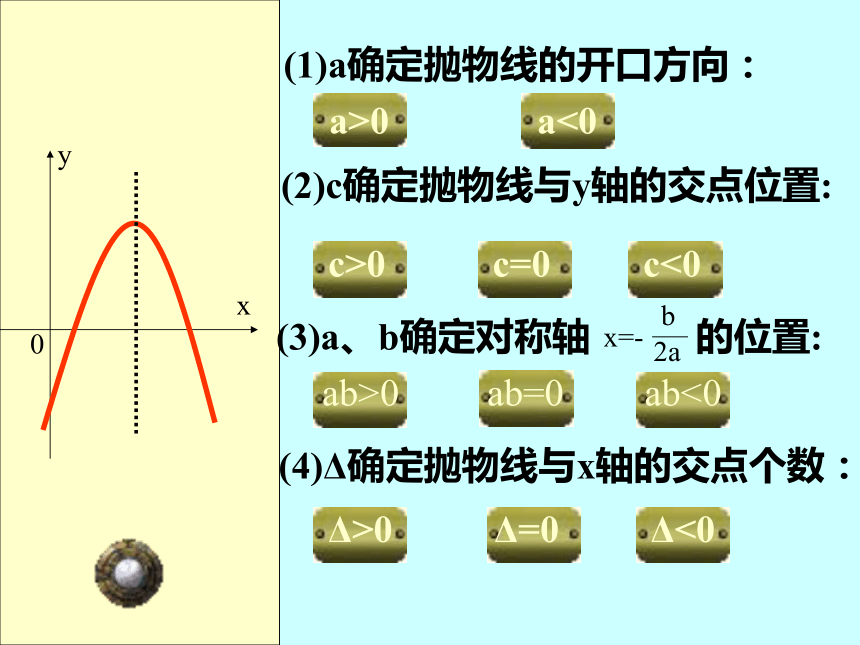
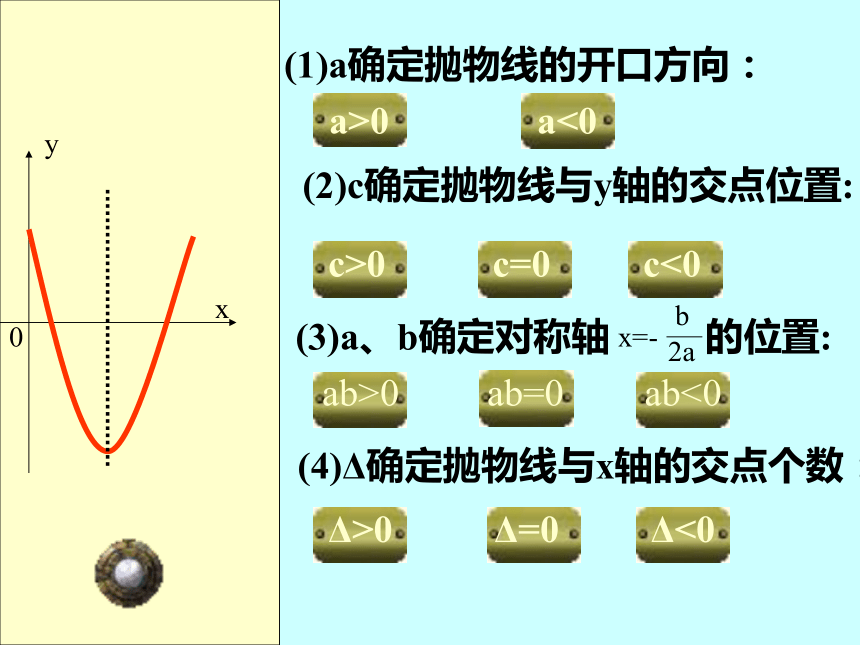
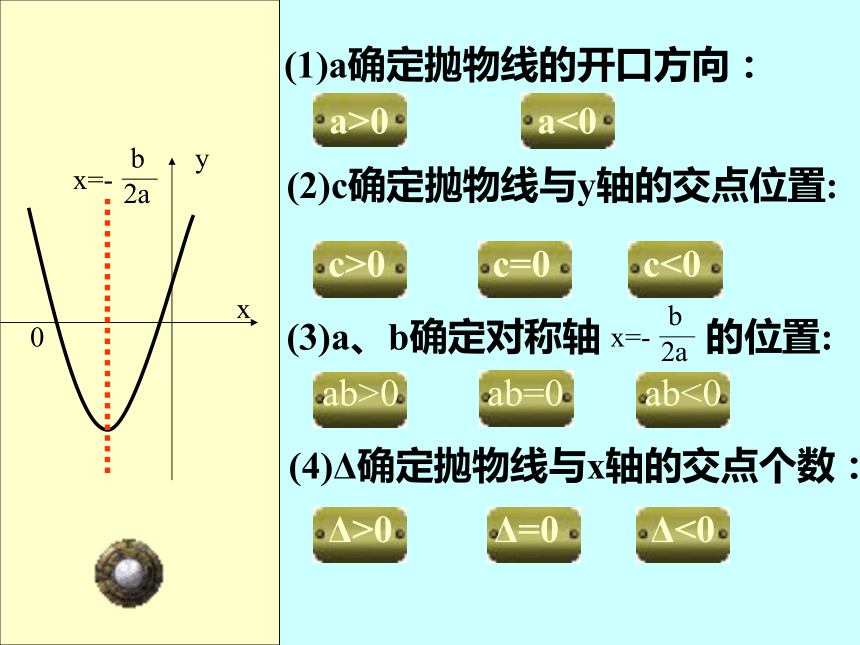
(1)a确定抛物线的开口方向:
a>0
a<0
(2)c确定抛物线与y轴的交点位置:
c>0
c=0
c<0
(3)a、b确定对称轴 的位置:
ab>0
ab=0
ab<0
(4)Δ确定抛物线与x轴的交点个数:
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
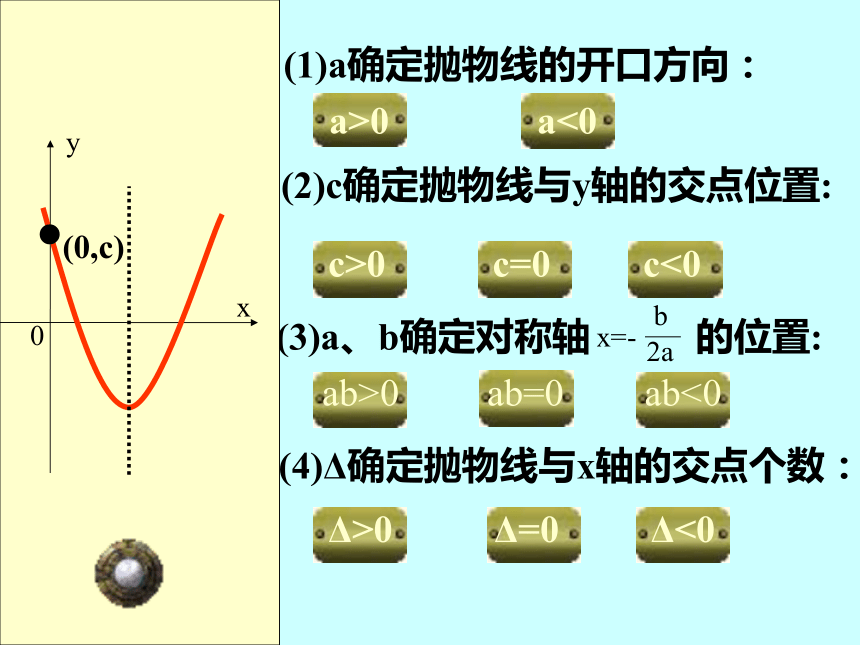
(1)a确定抛物线的开口方向:
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(0,c)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(0,0)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
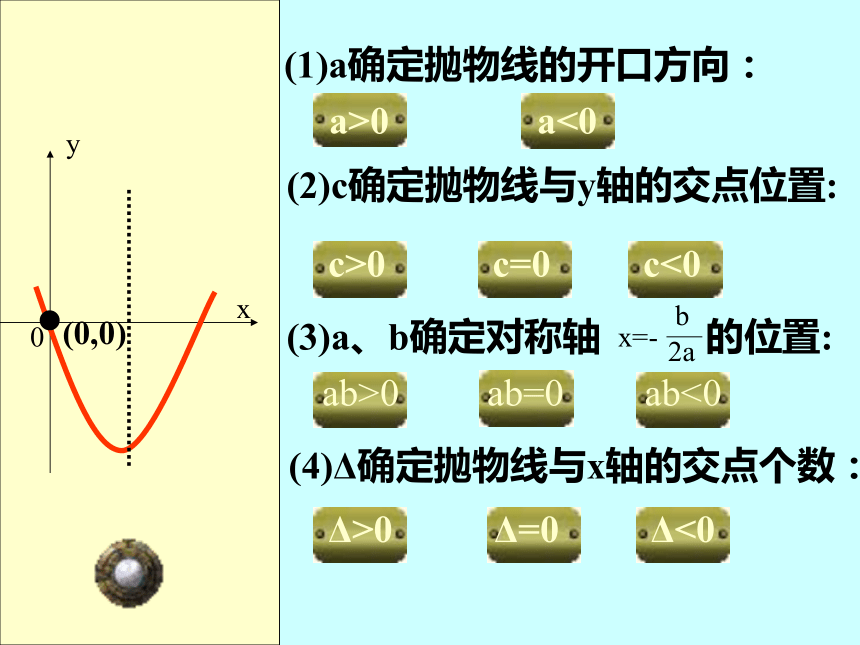
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(0,c)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
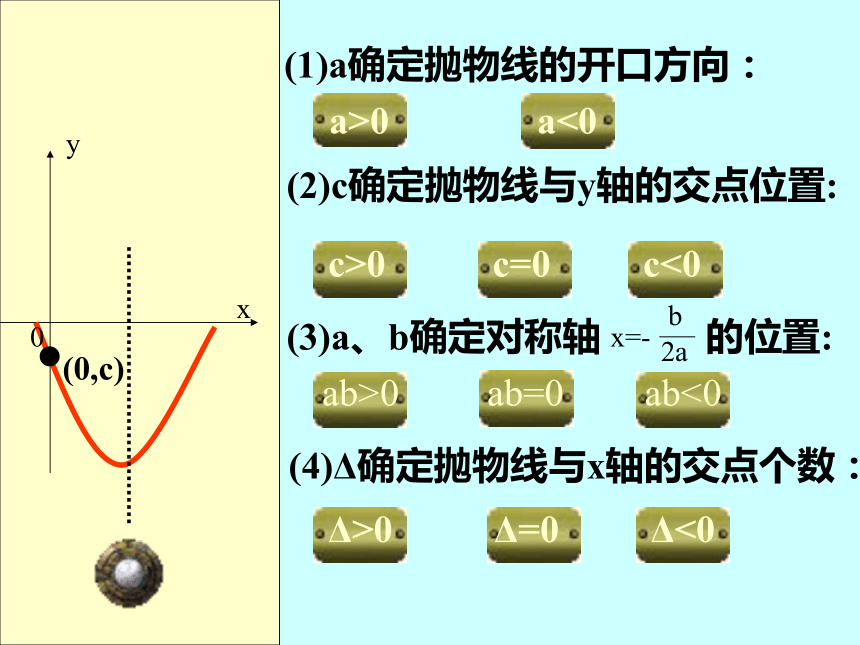
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
x=-
b
2a
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
x=-
b
2a
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
x=-
b
2a
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(x1,0)
(x2,0)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(x,0)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
两根式y=a(x-x1)(x-x2)
对称轴
二次函数图象与x轴的交点为
A(x1,0), B(x2,0);
AB=|x1-x2|=
顶点横坐标=
x
y
o
x2
x1
P
A
B
x1x2>0, 点A,点B在原点同侧
x1x2<0,点A,点B在原点两侧
x
y
o
A
B
x1
x2
A
B
x1
x2
A
B
x1
x2
A
B
x1
x2
根据条件恰当设二次函数解析式:
1.已知顶点在原点:
2.已知顶点在x轴:
3.已知顶点在y轴:
4.已知经过原点,则c值为0
例:已知二次函数
1.关于原点对称:
2.关于x轴对称:
3.关于y轴对称:
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解:(1)∵a= —>0
∴抛物线的开口向上
∵y= — (x2+2x+1)-2=—(x+1)2-2
∴对称轴x=-1,顶点坐标M(-1,-2)
1
2
1
2
1
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解:
(2)由x=0,得y= - -—
抛物线与y轴的交点C(0,- -—)
由y=0,得—x2+x- —=0
x1=-3 x2=1
与x轴交点A(-3,0)B(1,0)
3
2
3
2
3
2
1
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解
0
x
y
(3)
④连线
①画对称轴
x=-1
②确定顶点
(-1,-2)
(0,-–)
③确定与坐标轴的交点
及对称点
(-3,0)
(1,0)
3
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解
0
M(-1,-2)
C(0,-–)
A(-3,0)
B(1,0)
3
2
y
x
D
:(4)由对称性可知
MA=MB=√22+22=2√2
AB=|x1-x2|=4
∴ ΔMAB的周长=2MA+AB
=2 √2×2+4=4 √2+4
ΔMAB的面积=—AB×MD
=—×4×2=4
1
2
1
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解
解
0
x
x=-1
(0,-–)
(-3,0)
(1,0)
3
2
:(5)
(-1,-2)
当x=-1时,y有最小值为
y最小值=-2
当x<-1时,y随x的增大
而减小;
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解:
0
(-1,-2)
(0,-–)
(-3,0)
(1,0)
3
2
y
x
由图象可知
(6)
当x< -3或x>1时,y > 0
当-3 < x < 1时,y < 0
返回
你能否画出适当的函数图象,求方程
的解?
巩固练习
(1)二次函数y=x2-x-6的图象顶点坐标是___________对称轴是_________。
(2)抛物线y=-2x2+4x与x轴的交点坐标是___________
(3)已知函数y=—x2-x-4,当函数值y随x的增大而减小时,x的取值范围是___________
(4)二次函数y=mx2-3x+2m-m2的图象经过原点,则m= ____。
1
2
(—,-—)
1
25
2
4
x=—
1
2
(0,0)(2,0)
x<1
2
返回
例:已知抛物线y=ax2+bx+c与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此抛物线的解析式.
分析:此例题给出了三个条件,但实际上要看到此题还有隐含条件,如利用A点关于对称轴x=-1对称的对称点A′(1,0),因此可以把问题的条件又充实了,又如已知顶点M到x轴的距离为2,对称轴为x=-1,因此又可以找顶点坐标为(-1,±2),故可利用顶点坐标式求出函数的解析式,此题的解法不唯一 。
解法(一):∵抛物线的对称轴是x=-1,顶点M到x轴距离为2,
∴顶点的坐标为M(-1,2)或M′(-1,-2).
故设二次函数式y=a(x+1)2+2
或y=a(x+1)2-2
又∵抛物线经过点A(-3,0)
∴0=a(-3+1)2+2或0=a(-3+1)2-2
所求函数式是
解法(二):根据题意:
设函数解析式为y=ax2+bx+c
∵点A(-3,0)在抛物线上
∴0=9a-3b+c ①
又∵对称轴是x=-1
解法(三):∵抛物线的对称轴是x=-1
又∵图象经过点A(-3,0)
∴点A(-3,0)关于对称轴x=-1对称的对称点A′(1,0)
∴设函数式为y=a(x+3)(x-1)
把抛物线的顶点M的坐标(-1,2)或(-1,-2)分别代入函数式,得
2=a(-1+3)(-1-1)或-2=a(-1+3)(-1-1)
解关于a的方程,得
例.如图是二次函数y=ax2+bx+c的图象,判断以下各式的值是正值还是负值: (1)a;(2)b;
(3)c;(4)b2-4ac;
(5)2a+b;
(6)a+b+c;
(7)a-b+c;
(8)a+2b+4c.
例:已知抛物线y=ax2+bx+c,其顶点在x轴的上方,它与y轴交于点C(0,3),与x轴交于点A及点B(6,0).又知方程:ax2+bx+c=0(a≠0)两根平方和等于40.
(1)求抛物线的解析式;
(2)试问:在此抛物线上是否存在一点P,在x轴上方且使S△PAB=2S△CAB.如果存在,求出点P的坐标;如果不存在,说明理由.
1.如图,有一个二次函数的图象,三位学生分别说出了它的一些特点:
甲:对称轴是直线x=4。
乙:与x轴两个交点A、B点的横坐标
都是整数。
丙:与y轴的交点C点的纵坐标也是整数,
且S⊿ABC= 3。
请你写出满足上述条件的全部特点的所有的
二次函数的解析式为 。
O
C
A
B
x
y
x=4
例:已知:二次函数
y=x2+2ax-2b+1和
y=-x2+(a-3)x+b2-1
的图象都经过x轴上两个不同的点M、N,求 a,b的值.
例.抛物线y=ax2+bx+c与x轴的负半轴、正半轴分别相交于点A、点B,与y轴的正半轴相交于点C,且线段OB=2OC=2OA
① 求代数式abc的值;
② 若直线y=ax+b,经过点C,
求证:对一切实数x,代数式ax2+bx+c的值不大于
例.如果抛物线y= -x2+2(m-1)x+m+1与x轴交于A、B两点,且A点在x轴的正半轴上,B点在x轴的负半轴上,OA的长是a,OB的长是b.
(2)若a∶b=3∶1,求m的值,并写出此时抛物线的解析式;
(3)设(2)中的抛物线与y轴交于点C,抛物线的顶点是M,问:抛物线上是否存在点P,使△PAB的面积等于△BCM面积的8倍?若存在,求出P点坐标;若不存在,请说明理由.
(1)求m的取值范围
退出
一、定义
二、顶点与对称轴
三、解析式的求法
四、图象位置与
a、b、c、 的
正负关系
一、定义
二、顶点与对称轴
四、图象位置与
a、b、c、 的
正负关系
一般地,如果
y=ax2+bx+c(a,b,c
是常数,a≠0),那么,y
叫做x的二次函数。
三、解析式的求法
一、定义
二、顶点与对称轴
三、解析式的求法
四、图象位置与
a、b、c、 的
正负关系
y=ax2+bx+c
y=a(x+ )2+
b
2a
4ac-b2
4a
对称轴: x= –
b
2a
顶点坐标:(– , )
b
2a
4ac-b2
4a
一、定义
二、顶点与对称轴
三、解析式的求法
四、图象位置与
a、b、c、 的
正负关系
解析式 使用范围
一般式 已知任意
三个点
顶点式 已知顶点(h,k)及另一点
交点式 已知与x轴的两个交点及另一个点
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
(1)a确定抛物线的开口方向:
a>0
a<0
(2)c确定抛物线与y轴的交点位置:
c>0
c=0
c<0
(3)a、b确定对称轴 的位置:
ab>0
ab=0
ab<0
(4)Δ确定抛物线与x轴的交点个数:
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
(1)a确定抛物线的开口方向:
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(0,c)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(0,0)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(0,c)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
x=-
b
2a
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
x=-
b
2a
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
x=-
b
2a
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(x1,0)
(x2,0)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
(x,0)
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
(1)a确定抛物线的开口方向:
(2)c确定抛物线与y轴的交点位置:
(3)a、b确定对称轴 的位置:
(4)Δ确定抛物线与x轴的交点个数:
x
y
0
a>0
a<0
c>0
c=0
c<0
ab>0
ab=0
ab<0
Δ>0
Δ=0
Δ<0
x=-
b
2a
两根式y=a(x-x1)(x-x2)
对称轴
二次函数图象与x轴的交点为
A(x1,0), B(x2,0);
AB=|x1-x2|=
顶点横坐标=
x
y
o
x2
x1
P
A
B
x1x2>0, 点A,点B在原点同侧
x1x2<0,点A,点B在原点两侧
x
y
o
A
B
x1
x2
A
B
x1
x2
A
B
x1
x2
A
B
x1
x2
根据条件恰当设二次函数解析式:
1.已知顶点在原点:
2.已知顶点在x轴:
3.已知顶点在y轴:
4.已知经过原点,则c值为0
例:已知二次函数
1.关于原点对称:
2.关于x轴对称:
3.关于y轴对称:
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解:(1)∵a= —>0
∴抛物线的开口向上
∵y= — (x2+2x+1)-2=—(x+1)2-2
∴对称轴x=-1,顶点坐标M(-1,-2)
1
2
1
2
1
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解:
(2)由x=0,得y= - -—
抛物线与y轴的交点C(0,- -—)
由y=0,得—x2+x- —=0
x1=-3 x2=1
与x轴交点A(-3,0)B(1,0)
3
2
3
2
3
2
1
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解
0
x
y
(3)
④连线
①画对称轴
x=-1
②确定顶点
(-1,-2)
(0,-–)
③确定与坐标轴的交点
及对称点
(-3,0)
(1,0)
3
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解
0
M(-1,-2)
C(0,-–)
A(-3,0)
B(1,0)
3
2
y
x
D
:(4)由对称性可知
MA=MB=√22+22=2√2
AB=|x1-x2|=4
∴ ΔMAB的周长=2MA+AB
=2 √2×2+4=4 √2+4
ΔMAB的面积=—AB×MD
=—×4×2=4
1
2
1
2
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解
解
0
x
x=-1
(0,-–)
(-3,0)
(1,0)
3
2
:(5)
(-1,-2)
当x=-1时,y有最小值为
y最小值=-2
当x<-1时,y随x的增大
而减小;
例1:
已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两点,求C,
A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,y有最大
(小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?
1
2
3
2
解:
0
(-1,-2)
(0,-–)
(-3,0)
(1,0)
3
2
y
x
由图象可知
(6)
当x< -3或x>1时,y > 0
当-3 < x < 1时,y < 0
返回
你能否画出适当的函数图象,求方程
的解?
巩固练习
(1)二次函数y=x2-x-6的图象顶点坐标是___________对称轴是_________。
(2)抛物线y=-2x2+4x与x轴的交点坐标是___________
(3)已知函数y=—x2-x-4,当函数值y随x的增大而减小时,x的取值范围是___________
(4)二次函数y=mx2-3x+2m-m2的图象经过原点,则m= ____。
1
2
(—,-—)
1
25
2
4
x=—
1
2
(0,0)(2,0)
x<1
2
返回
例:已知抛物线y=ax2+bx+c与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此抛物线的解析式.
分析:此例题给出了三个条件,但实际上要看到此题还有隐含条件,如利用A点关于对称轴x=-1对称的对称点A′(1,0),因此可以把问题的条件又充实了,又如已知顶点M到x轴的距离为2,对称轴为x=-1,因此又可以找顶点坐标为(-1,±2),故可利用顶点坐标式求出函数的解析式,此题的解法不唯一 。
解法(一):∵抛物线的对称轴是x=-1,顶点M到x轴距离为2,
∴顶点的坐标为M(-1,2)或M′(-1,-2).
故设二次函数式y=a(x+1)2+2
或y=a(x+1)2-2
又∵抛物线经过点A(-3,0)
∴0=a(-3+1)2+2或0=a(-3+1)2-2
所求函数式是
解法(二):根据题意:
设函数解析式为y=ax2+bx+c
∵点A(-3,0)在抛物线上
∴0=9a-3b+c ①
又∵对称轴是x=-1
解法(三):∵抛物线的对称轴是x=-1
又∵图象经过点A(-3,0)
∴点A(-3,0)关于对称轴x=-1对称的对称点A′(1,0)
∴设函数式为y=a(x+3)(x-1)
把抛物线的顶点M的坐标(-1,2)或(-1,-2)分别代入函数式,得
2=a(-1+3)(-1-1)或-2=a(-1+3)(-1-1)
解关于a的方程,得
例.如图是二次函数y=ax2+bx+c的图象,判断以下各式的值是正值还是负值: (1)a;(2)b;
(3)c;(4)b2-4ac;
(5)2a+b;
(6)a+b+c;
(7)a-b+c;
(8)a+2b+4c.
例:已知抛物线y=ax2+bx+c,其顶点在x轴的上方,它与y轴交于点C(0,3),与x轴交于点A及点B(6,0).又知方程:ax2+bx+c=0(a≠0)两根平方和等于40.
(1)求抛物线的解析式;
(2)试问:在此抛物线上是否存在一点P,在x轴上方且使S△PAB=2S△CAB.如果存在,求出点P的坐标;如果不存在,说明理由.
1.如图,有一个二次函数的图象,三位学生分别说出了它的一些特点:
甲:对称轴是直线x=4。
乙:与x轴两个交点A、B点的横坐标
都是整数。
丙:与y轴的交点C点的纵坐标也是整数,
且S⊿ABC= 3。
请你写出满足上述条件的全部特点的所有的
二次函数的解析式为 。
O
C
A
B
x
y
x=4
例:已知:二次函数
y=x2+2ax-2b+1和
y=-x2+(a-3)x+b2-1
的图象都经过x轴上两个不同的点M、N,求 a,b的值.
例.抛物线y=ax2+bx+c与x轴的负半轴、正半轴分别相交于点A、点B,与y轴的正半轴相交于点C,且线段OB=2OC=2OA
① 求代数式abc的值;
② 若直线y=ax+b,经过点C,
求证:对一切实数x,代数式ax2+bx+c的值不大于
例.如果抛物线y= -x2+2(m-1)x+m+1与x轴交于A、B两点,且A点在x轴的正半轴上,B点在x轴的负半轴上,OA的长是a,OB的长是b.
(2)若a∶b=3∶1,求m的值,并写出此时抛物线的解析式;
(3)设(2)中的抛物线与y轴交于点C,抛物线的顶点是M,问:抛物线上是否存在点P,使△PAB的面积等于△BCM面积的8倍?若存在,求出P点坐标;若不存在,请说明理由.
(1)求m的取值范围
