黑龙江省宾县二高2020-2021学年高一下学期6月第三次月考数学试题 Word版含答案
文档属性
| 名称 | 黑龙江省宾县二高2020-2021学年高一下学期6月第三次月考数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 296.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 18:57:06 | ||
图片预览

文档简介
宾县二高2020-2021学年度下学期第三次月考
高一数学试卷
考试时间:120分钟;总分:150分
注意事项:1.答题前填写好自己的姓名、班级、考号等信息;2.请将答案规范填写在答题卡上。
一、选择题:(每题5分共60分。其中1-10为单选题,11,12为不定项选择题)
1.已知复数z满足false(i为虚部单位),则z的共轭复数的虚部为( )
A.2 B.false C.false D.false
2.向量false,且false,则实数false( )
A.3 B.false C.7 D.false
3.某高二年级有文科学生500人,理科学生1500人,为了解学生对数学的喜欢程度,现用分层抽样的方法从该年级抽取一个容量为60的样本,则样本中文科生的人数是( )
A.15 B.18 C.20 D.25
4.已知直线l与不同的平面false,则下列命题正确的是( )
A.若false,则false; B.若false,则false
C.若false,则false D.若false,则false
5.已知false是虚数单位,复数false与复平面内的点false对应,则复数false对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在△ABC中,若false2false2=false,则△ABC是( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等边三角形
7.false( )
A.false B.3 C.4 D.5
8.O为falseABCD的对角线的交点,false,false,则false等于( )
A.false B.false
C.false D.false
9.在false中,若false,则角false的值为( ).
A.30° B.60° C.45° D.90°
44100753048010.如图,已知圆柱的底面直径和高都等于球的直径,圆柱的表面积为false,则球的体积为 ( )
A.false B.false C.false D.false
11.已知false是不重合的直线,false是不重合的平面,则下列命题错误的是( )
A.若false,false,则false B.若false,false,则false
C.若false,false,则false且false D.若false,false,则false
12.对于false,有如下判断,其中正确的判断是( )
A.若false,false是钝角三角形
B.若false,则false
C.若false,则符合条件的false有两个
D.在三角形中,已知两边和一角就能求三角形的面积
填空题:(本大题共4小题,每小题5分,共20分)
13.已知在直四棱柱false,false,false,false,false,则异面直线false与false所成角的大小为___________.
14.在false中,false,则false___________.
15.如图,在棱长为1的正方体false中,点false是边false的中点,则false的体积为___________.
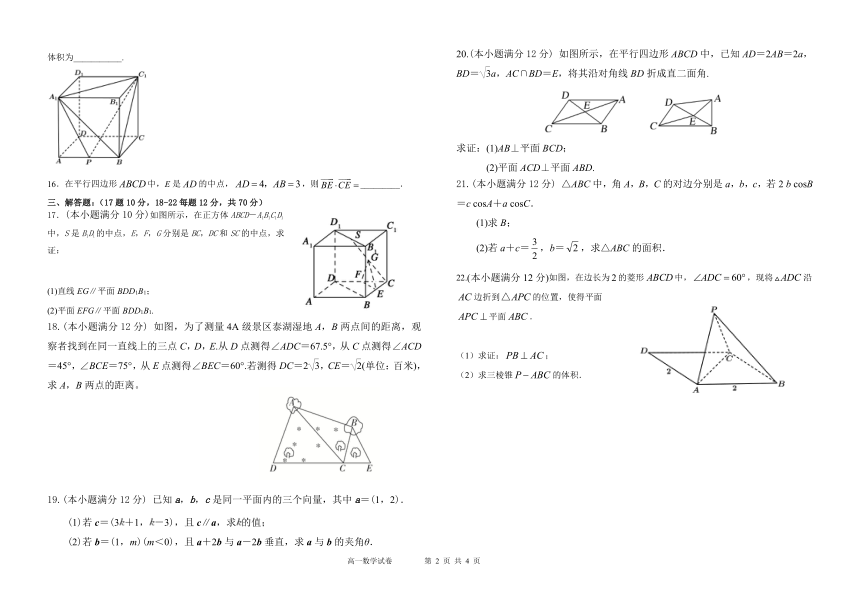
16.在平行四边形false中,E是false的中点,false,则false_________.
三、解答题:(17题10分,18-22每题12分,共70分)
3724275889017.(本小题满分10分)如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点,求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
3230245102616018.(本小题满分12分) 如图,为了测量4A级景区泰湖湿地A,B两点间的距离,观察者找到在同一直线上的三点C,D,E.从D点测得∠ADC=67.5°,从C点测得∠ACD=45°,∠BCE=75°,从E点测得∠BEC=60°.若测得DC=2,CE=(单位:百米),求A,B两点的距离。
19.(本小题满分12分) 已知a,b,c是同一平面内的三个向量,其中a=(1,2).
(1)若c=(3+1,-3),且c∥a,求的值;
(2)若b=(1,m)(m<0),且a+2b与a-2b垂直,求a与b的夹角θ.
20.(本小题满分12分) 如图所示,在平行四边形ABCD中,已知AD=2AB=2a,BD=a,AC∩BD=E,将其沿对角线BD折成直二面角.
求证:(1)AB⊥平面BCD;
(2)平面ACD⊥平面ABD.
21.(本小题满分12分) △ABC中,角A,B,C的对边分别是a,b,c,若2 b cosB=c cosA+a cosC.
(1)求B;
(2)若a+c=false,b=false,求△ABC的面积.
276225052959022.(本小题满分12分)如图,在边长为false的菱形false中,false,现将false沿false边折到false的位置,使得平面false平面false.
(1)求证:false;
(2)求三棱锥false的体积.
宾县二高2020-2021学年度高一下学期第三次月考
高一数学答案
一、单项选择题:
1
2
3
4
5
6
7
8
9
10
11
12
A
D
A
B
D
C
A
B
C
B
ABC
ABD
填空题(本大题共4小题,每小题5分,共20分。)
13、false
14、2
15、false
16、false
三、解答题:
17.试题解析:(1)连结SB,由已知得EG∥SB,由此能证明直线EG∥平面BDD1B1.
(2)连结SD,由已知得FG∥SD,
从而FG∥平面BDD1B1,
又直线EG∥平面BDD1B1,
(2)由此能证明平面EFG∥平面BDD1B1.
18.(本小题满分12分)
解析 根据题意,在△ADC中,∠ACD=45°,∠ADC=67.5°,DC=2,则∠DAC=180°-45°-67.5°=67.5°, ………1分
则AC=DC=2, ………3分
在△BCE中,∠BCE=75°,∠BEC=60°,CE=,则∠EBC=180°-75°-60°=45°,则=, ………6分
变形得BC===, ………8分
在△ABC中,AC=2,BC=,∠ACB=180°-∠ACD-∠BCE=60°,则AB2=AC2+BC2-2AC·BC·cos∠ACB=9,则AB=3. ………12分
19. 解:(1)因为c=(3+1,-3),且c∥a,所以
(3+1)×2-(-3)×1=0, ………2分
解得=-1; ………4分
(2)由题意,可知false ………6分
因为a+2b与a-2b垂直,所以(a+2b)·(a-2b)=0, ………7分
即(2+2m)(2-2m)=3,m<0解得m=-false,则b=(1,-false), ………9分
所以a·b=0,于是θ=false. ………10分
20.证明 (1)在△ABD中,AB=a,AD=2a,BD=a,
∴AB2+BD2=AD2,∴∠ABD=90°,AB⊥BD.
又∵平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,AB?平面ABD,
∴AB⊥平面BCD.
(2)∵折叠前四边形ABCD是平行四边形,且AB⊥BD,
∴CD⊥BD.∵AB⊥平面BCD,CD?平面BCD,∴AB⊥CD.
∵AB∩BD=B,AB,BD?平面ABD,
∴CD⊥平面ABD.
又∵CD?平面ACD,
∴平面ACD⊥平面ABD.
21.解 (1)由正弦定理得
2sinBcosB=sinCcosA+sinAcosC, ………2分
即2sinBcosB=sin(A+C), ………3分
又A+C=π-B,∴2sinBcosB=sin(π-B),
即2sinBcosB=sinB. ………4分
而sinB≠0,∴cosB=,由0 (2)∵cosB==, ………7分
∴=,又a+c=false,b=false, ………9分
∴false-2ac-2=ac,即ac=false, ………10分
∴S△ABC=acsinB=×false×=false. ………12分
22.证明:(1)如图所示,取false的中点为false,连接false、false,因为四边形false为菱形,由false,得false,由false,得false,
又false,false平面false,
而false平面false,所以false;
(2)由(1)知,false,又平面false平面false,
且平面false平面false,false平面false,
由已知可得,false,false,
false.
高一数学试卷
考试时间:120分钟;总分:150分
注意事项:1.答题前填写好自己的姓名、班级、考号等信息;2.请将答案规范填写在答题卡上。
一、选择题:(每题5分共60分。其中1-10为单选题,11,12为不定项选择题)
1.已知复数z满足false(i为虚部单位),则z的共轭复数的虚部为( )
A.2 B.false C.false D.false
2.向量false,且false,则实数false( )
A.3 B.false C.7 D.false
3.某高二年级有文科学生500人,理科学生1500人,为了解学生对数学的喜欢程度,现用分层抽样的方法从该年级抽取一个容量为60的样本,则样本中文科生的人数是( )
A.15 B.18 C.20 D.25
4.已知直线l与不同的平面false,则下列命题正确的是( )
A.若false,则false; B.若false,则false
C.若false,则false D.若false,则false
5.已知false是虚数单位,复数false与复平面内的点false对应,则复数false对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在△ABC中,若false2false2=false,则△ABC是( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等边三角形
7.false( )
A.false B.3 C.4 D.5
8.O为falseABCD的对角线的交点,false,false,则false等于( )
A.false B.false
C.false D.false
9.在false中,若false,则角false的值为( ).
A.30° B.60° C.45° D.90°
44100753048010.如图,已知圆柱的底面直径和高都等于球的直径,圆柱的表面积为false,则球的体积为 ( )
A.false B.false C.false D.false
11.已知false是不重合的直线,false是不重合的平面,则下列命题错误的是( )
A.若false,false,则false B.若false,false,则false
C.若false,false,则false且false D.若false,false,则false
12.对于false,有如下判断,其中正确的判断是( )
A.若false,false是钝角三角形
B.若false,则false
C.若false,则符合条件的false有两个
D.在三角形中,已知两边和一角就能求三角形的面积
填空题:(本大题共4小题,每小题5分,共20分)
13.已知在直四棱柱false,false,false,false,false,则异面直线false与false所成角的大小为___________.
14.在false中,false,则false___________.
15.如图,在棱长为1的正方体false中,点false是边false的中点,则false的体积为___________.
16.在平行四边形false中,E是false的中点,false,则false_________.
三、解答题:(17题10分,18-22每题12分,共70分)
3724275889017.(本小题满分10分)如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点,求证:
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
3230245102616018.(本小题满分12分) 如图,为了测量4A级景区泰湖湿地A,B两点间的距离,观察者找到在同一直线上的三点C,D,E.从D点测得∠ADC=67.5°,从C点测得∠ACD=45°,∠BCE=75°,从E点测得∠BEC=60°.若测得DC=2,CE=(单位:百米),求A,B两点的距离。
19.(本小题满分12分) 已知a,b,c是同一平面内的三个向量,其中a=(1,2).
(1)若c=(3+1,-3),且c∥a,求的值;
(2)若b=(1,m)(m<0),且a+2b与a-2b垂直,求a与b的夹角θ.
20.(本小题满分12分) 如图所示,在平行四边形ABCD中,已知AD=2AB=2a,BD=a,AC∩BD=E,将其沿对角线BD折成直二面角.
求证:(1)AB⊥平面BCD;
(2)平面ACD⊥平面ABD.
21.(本小题满分12分) △ABC中,角A,B,C的对边分别是a,b,c,若2 b cosB=c cosA+a cosC.
(1)求B;
(2)若a+c=false,b=false,求△ABC的面积.
276225052959022.(本小题满分12分)如图,在边长为false的菱形false中,false,现将false沿false边折到false的位置,使得平面false平面false.
(1)求证:false;
(2)求三棱锥false的体积.
宾县二高2020-2021学年度高一下学期第三次月考
高一数学答案
一、单项选择题:
1
2
3
4
5
6
7
8
9
10
11
12
A
D
A
B
D
C
A
B
C
B
ABC
ABD
填空题(本大题共4小题,每小题5分,共20分。)
13、false
14、2
15、false
16、false
三、解答题:
17.试题解析:(1)连结SB,由已知得EG∥SB,由此能证明直线EG∥平面BDD1B1.
(2)连结SD,由已知得FG∥SD,
从而FG∥平面BDD1B1,
又直线EG∥平面BDD1B1,
(2)由此能证明平面EFG∥平面BDD1B1.
18.(本小题满分12分)
解析 根据题意,在△ADC中,∠ACD=45°,∠ADC=67.5°,DC=2,则∠DAC=180°-45°-67.5°=67.5°, ………1分
则AC=DC=2, ………3分
在△BCE中,∠BCE=75°,∠BEC=60°,CE=,则∠EBC=180°-75°-60°=45°,则=, ………6分
变形得BC===, ………8分
在△ABC中,AC=2,BC=,∠ACB=180°-∠ACD-∠BCE=60°,则AB2=AC2+BC2-2AC·BC·cos∠ACB=9,则AB=3. ………12分
19. 解:(1)因为c=(3+1,-3),且c∥a,所以
(3+1)×2-(-3)×1=0, ………2分
解得=-1; ………4分
(2)由题意,可知false ………6分
因为a+2b与a-2b垂直,所以(a+2b)·(a-2b)=0, ………7分
即(2+2m)(2-2m)=3,m<0解得m=-false,则b=(1,-false), ………9分
所以a·b=0,于是θ=false. ………10分
20.证明 (1)在△ABD中,AB=a,AD=2a,BD=a,
∴AB2+BD2=AD2,∴∠ABD=90°,AB⊥BD.
又∵平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,AB?平面ABD,
∴AB⊥平面BCD.
(2)∵折叠前四边形ABCD是平行四边形,且AB⊥BD,
∴CD⊥BD.∵AB⊥平面BCD,CD?平面BCD,∴AB⊥CD.
∵AB∩BD=B,AB,BD?平面ABD,
∴CD⊥平面ABD.
又∵CD?平面ACD,
∴平面ACD⊥平面ABD.
21.解 (1)由正弦定理得
2sinBcosB=sinCcosA+sinAcosC, ………2分
即2sinBcosB=sin(A+C), ………3分
又A+C=π-B,∴2sinBcosB=sin(π-B),
即2sinBcosB=sinB. ………4分
而sinB≠0,∴cosB=,由0
∴=,又a+c=false,b=false, ………9分
∴false-2ac-2=ac,即ac=false, ………10分
∴S△ABC=acsinB=×false×=false. ………12分
22.证明:(1)如图所示,取false的中点为false,连接false、false,因为四边形false为菱形,由false,得false,由false,得false,
又false,false平面false,
而false平面false,所以false;
(2)由(1)知,false,又平面false平面false,
且平面false平面false,false平面false,
由已知可得,false,false,
false.
同课章节目录
