1.3集合的基本运算-【新教材】人教A版(2019)高中数学必修第一册知识点总结与例题讲解(Word含答案解析)
文档属性
| 名称 | 1.3集合的基本运算-【新教材】人教A版(2019)高中数学必修第一册知识点总结与例题讲解(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 19:01:59 | ||
图片预览




文档简介
集合的基本运算知识点总结与例题讲解
本节知识点:
(1)并集.
(2)交集.
(3)全集与补集.
(4)德·摩根定律.
知识点一 并集
自然语言 一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与集合B的并集,记作,读作“A并B”.
符号语言 .
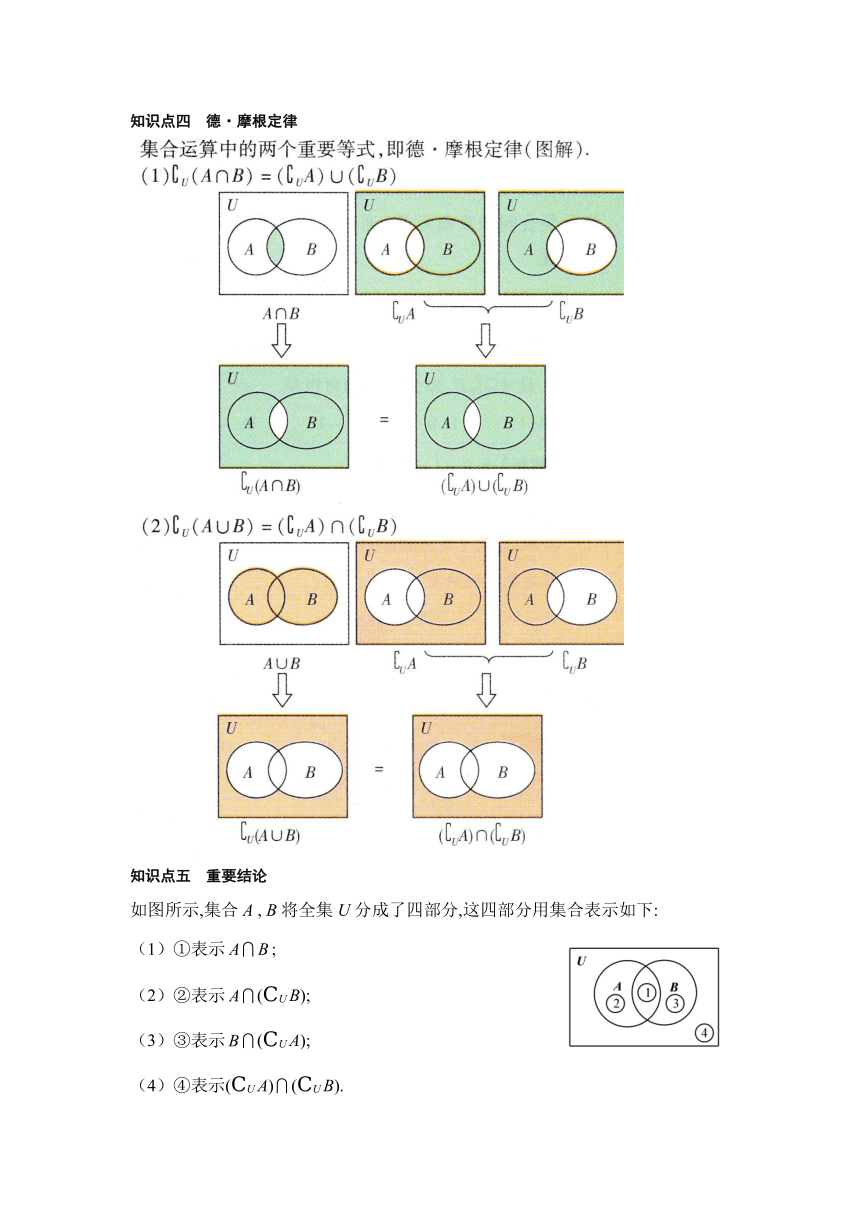
图形语言(用Venn图表示并集) 图中阴影部分表示两个集合的并集.
(1)A与B有公共元素,相互不包含 (2)A与B没有公共部分
(3) (4)
(5)
对并集的理解
(1)求两个集合的并集是集合的一种运算,结果仍是一个集合,它是由属于集合A或集合B的元素组成的.
(2)并集概念中的“或”指的是只要满足其中一个条件即可.符号语言“”分为三种情况:
①,但; ②,但; ③,且.
(3)根据集合元素的互异性,在求两个集合的并集时,两个集合中的公共元素在并集中只能出现一次.
并集的性质
性质 说明
并集运算满足交换律
并集运算满足结合律
任何集合与空集的并集等于这个集合本身
任何集合与其本身的并集等于这个集合本身
若,则 并集运算与子集关系的转化
, 任何集合都是该集合与另一个集合的并集的子集
求并集的方法
(1)求两个有限集的并集 按照并集的定义进行计算,但要特别注意集合元素的互异性.
(2)求两个无限集的并集 借助于数轴进行计算.注意两个集合的并集等于这两个集合在数轴上对应的图形所覆盖的全部范围.
知识点二 交集
自然语言 一般地,由属于集合A且属于集合B的所有元素组成的集合,称为集合A与集合B的交集,记作,读作“A交B”.
符号语言 .
图形语言(用Venn图表示交集) 图中阴影部分表示两个集合的并集.
如下页图所示.
(1)A与B有部分公共元素 (2)A与B无公共元素,
(3)若,则(4)若,则(5)
对交集的理解
(1)求两个集合的交集是集合的一种运算,结果仍是一个集合,它是由属于集合A且属于集合B的所有元素组成的集合,及两个集合的公共元素所组成的集合.
(2)交集概念中的“所有”二字不能省略,否则会漏掉一些元素,一定要将两个集合中的相同元素(公共元素)全部找出来.
(3)当集合A与集合B没有公共元素时,不能说集合A与集合B没有交集,而是交集为空集,.
交集的性质
性质 说明
交集运算满足交换律
任何集合与空集的交集都是空集
任何集合与其本身的交集等于这个集合本身
交集运算满足结合律
满足分配律
若,则 交集运算与子集关系的转化
两个集合的交集是其中任何一个集合的子集
求交集的方法
(1)求两个有限集的交集 按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.
(2)求两个无限集的交集 借助于数轴进行计算.两个集合的交集等于这两个集合在数轴上对应的图形所覆盖的公共范围.
知识点三 全集与补集
全集 一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,记作U.
补集 对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集,简称集合A的补集,记作CU A,即
CU A.
用Venn图表示为:
对补集的理解
(1)补集是相对于全集而言的,求一个集合的补集,结果因全集的不同而不同.所以求补集前,要先明确全集.
(2)补集既是集合间的一种关系,同时也是集合之间的一种运算.
(3)符号“CU A”有三层意思:
① CU A;
② CU A是U的一个子集,及(CU A);
③ CU A表示一个集合.
补集的性质
①(CU A); ②(CU A); ③ CU (CU A);
④ CU U; ⑤ CU.
知识点四 德·摩根定律
知识点五 重要结论
如图所示,集合A , B将全集U分成了四部分,这四部分用集合表示如下:
(1)①表示;
(2)②表示(CU B);
(3)③表示(CU A);
(4)④表示(CU A)(CU B).
知识点六 集合中元素的个数
若集合A为有限集,则用card(A)表示集合A中元素的个数.
如果集合A中含有个元素,那么有card(A).
(1)一般地,对于任意两个有限集合A , B,有
cardcard(A)card(B)-card.
(2)一般地,对于任意三个有限集合A , B , C,有
cardcard(A)card(B)-card-card-card+
card.
例题讲解
题型一 并集运算
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与集合B的并集,记作,读作“A并B”.即
.
求并集的方法
(1)求两个有限集的并集 按照并集的定义进行计算,但要特别注意集合元素的互异性.
(2)求两个无限集的并集 借助于数轴进行计算.注意两个集合的并集等于这两个集合在数轴上对应的图形所覆盖的全部范围.
例1. 已知集合,,则【 】
(A) (B)
(C) (D)
分析:将一个用描述法表示的集合转化为用列举法表示时,一定要弄清代表元素的含义或特征.
求两个集合的并集运算时,可以按照并集的定义进行,也可以用Venn图求解或借助于数轴求解.
解:∵
∴.
选择【 D 】.
例2. 已知集合,,则____________.
分析:先解一元二次不等式,求出集合B,然后把集合A、B在数轴上画出来,它们对应图形所覆盖的全部范围即为.
解:∵
∴.
例3. 已知集合,,若,则等于【 】
(A)0或 (B)0或3
(C)1或 (D)1或3
分析:,由集合元素的互异性,得,排除C、D选项.
因为,根据并集的性质,所以,这样就将两个集合的并集运算转化为了这两个集合之间的关系,从而可以确定参数的值或取值范围.
解:∵,∴或
当时,解之得:(不符合题意,舍去)
综上,或.
例4. 已知集合,,若,则实数的取值范围是__________.
分析:∵,∴.
解:
∵,∴,∴
∴实数的取值范围是.
例5. 已知集合,,且,求的值.
分析:由题意可知:,所以,从而,且.
解:分为三种情况:
①当时,解之得:(不符合题意,舍去);
②当时,解之得:;
③当时,解之得:.
综上所述,的值为0或或.
注意:在求参数的值时,参数的值要满足集合元素的互异性.
例6. 已知集合,,求.
分析:对于含参集合参与的集合运算,要注意分类讨论.
解:,.
当≤5,即≤8时,;
当时,即时,R.
例7.(易错题)已知集合,,且,求由的取值构成的集合.
分析:因为,所以.由于集合B是一个含参集合,所以要对集合B分和两种情况进行讨论.
解:∵,∴.
当时,,满足;
当时,或:
①若,则,解之得:;
②若,则,解之得:.
综上所述,的取值构成的集合为.
例8. 设集合,,若,则实数的取值范围是__________.
分析:先将并集运算的结果转化为两个集合M , N之间的关系,从而列出关于参数的不等式(组)求解.注意含参集合的分类讨论.
解:∵,∴.
分为两种情况:
①当时,有≥,解之得:≤;
②当时,则有:
,解之得:≤2.
综上所述,实数的取值范围是.
警示:在解决本题时,任意忽略的情况,另外要注意端点值能否取到.
例9. 已知集合,,若,求实数的取值范围.
分析:注意本题与例7的区别.
解:∵,∴.
分为三种情况:
①当时,恒成立,∴R,满足;
②当时,,有,解之得:
∴;
③当时,,有,解之得:
∴.
综上所述,实数的取值范围是.
题型二 交集运算
一般地,由属于集合A且属于集合B的所有元素组成的集合,称为集合A与集合B的交集,记作,读作“A交B”.
.
求交集的方法
(1)求两个有限集的交集 按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.(或可借助于Venn图)
(2)求两个无限集的交集 借助于数轴进行计算.两个集合的解集等于这两个集合在数轴上对应的图形所覆盖的公共范围.
例10. 设集合,集合,则【 】
(A) (B)
(C) (D)
分析:在进行集合的运算之前,要先弄清楚各个集合的本质.本题中集合A的代表元素为整数,所以集合A为范围内的整数集.
解:∵,
∴.
选择【 D 】.
例11. 设集合,,若,则实数的取值范围是__________.
分析:说明集合A、B有公共元素,在数轴上集合A、B所对应的图形覆盖的区域有公共部分.
解:.
例12. 设集合,,若,求实数的取值范围.
分析:若,则由交集的性质知,在得到这两个集合之间的关系后借助于数轴就可以列出不等式(组)进行求解了.
解:∵,∴.
分为两种情况:
①当时,满足,有≥,解之得:≤;
②当时,则有:
,解之得:≤2.
综上所述,实数的取值范围是.
★例13.(易错题)设集合,,则等于【 】
(A) (B)
(C) (D)
错解:解方程组得:或,故选【 C 】.
错因分析:这里好多学生认为是求抛物线和直线的交点坐标所构成的集合,根源在于没有搞清楚集合A , B的本质,没有弄清楚集合的代表元素的特征.
分析:本题中的两个集合都是由函数值构成的,它们的代表元素是函数值.表示函数和函数的函数值的交集.
解:∵,R.
∴R.
选择【 A 】.
变式: 设集合,,则等于【 】
(A) (B)
(C) (D)
例14. 已知集合,集合,则中元素的个数为【 】
(A)3 (B)2 (C)1 (D)0
解:解方程组得:
或
∴,共有2个元素.选择【 B 】.
方法二:由后面的学习可以知道,方程是单位圆的方程(以原点为圆心,以1为半径的圆).集合A是由圆上的所有点构成的,集合B是由直线上的所有点构成的,所以就是由单位圆与直线的交点构成的,如图所示,交点有两个,故中元素的个数为2.
例15.(2018沈阳重点高中)设集合,.
(1)若,求A的非空真子集的个数;
(2)若,求实数的取值范围.
分析:(1)子集、真子集个数的确定
若集合A含有个元素,则集合A:
(1)含有个子集;
(2)含有个非空子集;
(3)含有个真子集;
(4)含有个非空真子集.
(2)若,则,注意分类讨论.
解:(1)
∵集合A中含有8个元素
∴集合A的非空真子集的个数为;
(2)∵,∴.
分为两种情况:
①当时,满足,有,解之得:;
②当时,则有:
,解之得:≤≤3.
综上所述,实数的取值范围是.
例16. 设,,其中R,如果,求实数的取值范围.
解:
∵,∴
分为两种情况:
①当时,满足
∴,解之得:;
②当时,或或.
若或,则有,解之得:
经检验,此时;
若,则由根与系数的关系定理可得:
,解之得:.
综上所述,实数的取值范围是.
例17. 设集合,,若,求实数的取值范围.
分析:对于任意实数,都有,所以本题中集合A不会是空集.
解:∵,∴.
∵
∴,解之得:≤≤2.
∴实数的取值范围是.
★★例18.(综合性强)已知集合,集合,若:
(1)求实数的取值范围;
(2)当恒成立时,求的最小值.
分析:(1)求集合A时要解含参一元二次不等式,可借助于因式分解:
对于集合B,代表元素是,所以集合B是函数值的集合,通过配方得:
∵0≤≤3,∴2≤≤4,∴;
(2)这是与二次函数有关的恒成立问题,使用数形结合方法.
解:(1)
∵(这里作差比较与的大小)
∴
∴.
∵
∴,解之得:≤或≤≤2.
∴实数的取值范围是;
(2)∵恒成立,即≥0恒成立.
∴≤0,解之得:≤≤2.
∴的最小值为.
题型三 补集运算
全集 一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,记作U.
补集 对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集,简称集合A的补集,记作CU A,即
CU A.
补集的性质
①(CU A); ②(CU A); ③ CU (CU A);
④ CU U; ⑤ CU.
例19. 已知全集,集合,若CUA,则实数的取值范围是__________.
分析: CUA说明,且.
解:∵CUA,∴,且.
∴实数的取值范围是.
例20. 已知全集,集合,求CUA.
分析:集合A是由方程的解构成的,而方程可能无解、有两个不相等的实数根或有两个相等的实数根,需要分类讨论.
解:由题意可知:.
分为两种情况:
①当时,方程无实数根,∴,解之得:
∴CUACU;
②当时,则有≥0,解之得:≤或≥4.
设方程的两个实数根分别为
由根与系数的关系定理可得::
若,则,符合题意,此时,CUA;
若,则,符合题意,此时,CUA.
综上所述,当时,CUA;
当时,CUA;
当时,CUA.
例21. 已知,.
(1)当时,求;
(2)若CRA,求实数的取值范围.
分析:(1)求两个连续型实数集合的并集时,借助于数轴进行求解能将抽象的问题直观化,但要特别注意端点的实心和空心以及端点值的取舍;(2)求连续型实数集合的补集也是借助于数轴进行.
解:(1)当时,
∴;
(2)∵,∴CRA
∵CRA,∴分为两种情况:
①当时,有≥,解之得:≤;
②当时,则有:或
解之得:无解或.
综上,实数的取值范围是.
★例22. 设全集,,,求CIA.
解:
∴集合A是由直线上除点外的所有点构成的集合
∴CIA
∵
∴集合B是由直线上所有的点构成的集合
∴CIA.
附:函数,即的图象如图所示.
本节知识点:
(1)并集.
(2)交集.
(3)全集与补集.
(4)德·摩根定律.
知识点一 并集
自然语言 一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与集合B的并集,记作,读作“A并B”.
符号语言 .
图形语言(用Venn图表示并集) 图中阴影部分表示两个集合的并集.
(1)A与B有公共元素,相互不包含 (2)A与B没有公共部分
(3) (4)
(5)
对并集的理解
(1)求两个集合的并集是集合的一种运算,结果仍是一个集合,它是由属于集合A或集合B的元素组成的.
(2)并集概念中的“或”指的是只要满足其中一个条件即可.符号语言“”分为三种情况:
①,但; ②,但; ③,且.
(3)根据集合元素的互异性,在求两个集合的并集时,两个集合中的公共元素在并集中只能出现一次.
并集的性质
性质 说明
并集运算满足交换律
并集运算满足结合律
任何集合与空集的并集等于这个集合本身
任何集合与其本身的并集等于这个集合本身
若,则 并集运算与子集关系的转化
, 任何集合都是该集合与另一个集合的并集的子集
求并集的方法
(1)求两个有限集的并集 按照并集的定义进行计算,但要特别注意集合元素的互异性.
(2)求两个无限集的并集 借助于数轴进行计算.注意两个集合的并集等于这两个集合在数轴上对应的图形所覆盖的全部范围.
知识点二 交集
自然语言 一般地,由属于集合A且属于集合B的所有元素组成的集合,称为集合A与集合B的交集,记作,读作“A交B”.
符号语言 .
图形语言(用Venn图表示交集) 图中阴影部分表示两个集合的并集.
如下页图所示.
(1)A与B有部分公共元素 (2)A与B无公共元素,
(3)若,则(4)若,则(5)
对交集的理解
(1)求两个集合的交集是集合的一种运算,结果仍是一个集合,它是由属于集合A且属于集合B的所有元素组成的集合,及两个集合的公共元素所组成的集合.
(2)交集概念中的“所有”二字不能省略,否则会漏掉一些元素,一定要将两个集合中的相同元素(公共元素)全部找出来.
(3)当集合A与集合B没有公共元素时,不能说集合A与集合B没有交集,而是交集为空集,.
交集的性质
性质 说明
交集运算满足交换律
任何集合与空集的交集都是空集
任何集合与其本身的交集等于这个集合本身
交集运算满足结合律
满足分配律
若,则 交集运算与子集关系的转化
两个集合的交集是其中任何一个集合的子集
求交集的方法
(1)求两个有限集的交集 按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.
(2)求两个无限集的交集 借助于数轴进行计算.两个集合的交集等于这两个集合在数轴上对应的图形所覆盖的公共范围.
知识点三 全集与补集
全集 一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,记作U.
补集 对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集,简称集合A的补集,记作CU A,即
CU A.
用Venn图表示为:
对补集的理解
(1)补集是相对于全集而言的,求一个集合的补集,结果因全集的不同而不同.所以求补集前,要先明确全集.
(2)补集既是集合间的一种关系,同时也是集合之间的一种运算.
(3)符号“CU A”有三层意思:
① CU A;
② CU A是U的一个子集,及(CU A);
③ CU A表示一个集合.
补集的性质
①(CU A); ②(CU A); ③ CU (CU A);
④ CU U; ⑤ CU.
知识点四 德·摩根定律
知识点五 重要结论
如图所示,集合A , B将全集U分成了四部分,这四部分用集合表示如下:
(1)①表示;
(2)②表示(CU B);
(3)③表示(CU A);
(4)④表示(CU A)(CU B).
知识点六 集合中元素的个数
若集合A为有限集,则用card(A)表示集合A中元素的个数.
如果集合A中含有个元素,那么有card(A).
(1)一般地,对于任意两个有限集合A , B,有
cardcard(A)card(B)-card.
(2)一般地,对于任意三个有限集合A , B , C,有
cardcard(A)card(B)-card-card-card+
card.
例题讲解
题型一 并集运算
一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与集合B的并集,记作,读作“A并B”.即
.
求并集的方法
(1)求两个有限集的并集 按照并集的定义进行计算,但要特别注意集合元素的互异性.
(2)求两个无限集的并集 借助于数轴进行计算.注意两个集合的并集等于这两个集合在数轴上对应的图形所覆盖的全部范围.
例1. 已知集合,,则【 】
(A) (B)
(C) (D)
分析:将一个用描述法表示的集合转化为用列举法表示时,一定要弄清代表元素的含义或特征.
求两个集合的并集运算时,可以按照并集的定义进行,也可以用Venn图求解或借助于数轴求解.
解:∵
∴.
选择【 D 】.
例2. 已知集合,,则____________.
分析:先解一元二次不等式,求出集合B,然后把集合A、B在数轴上画出来,它们对应图形所覆盖的全部范围即为.
解:∵
∴.
例3. 已知集合,,若,则等于【 】
(A)0或 (B)0或3
(C)1或 (D)1或3
分析:,由集合元素的互异性,得,排除C、D选项.
因为,根据并集的性质,所以,这样就将两个集合的并集运算转化为了这两个集合之间的关系,从而可以确定参数的值或取值范围.
解:∵,∴或
当时,解之得:(不符合题意,舍去)
综上,或.
例4. 已知集合,,若,则实数的取值范围是__________.
分析:∵,∴.
解:
∵,∴,∴
∴实数的取值范围是.
例5. 已知集合,,且,求的值.
分析:由题意可知:,所以,从而,且.
解:分为三种情况:
①当时,解之得:(不符合题意,舍去);
②当时,解之得:;
③当时,解之得:.
综上所述,的值为0或或.
注意:在求参数的值时,参数的值要满足集合元素的互异性.
例6. 已知集合,,求.
分析:对于含参集合参与的集合运算,要注意分类讨论.
解:,.
当≤5,即≤8时,;
当时,即时,R.
例7.(易错题)已知集合,,且,求由的取值构成的集合.
分析:因为,所以.由于集合B是一个含参集合,所以要对集合B分和两种情况进行讨论.
解:∵,∴.
当时,,满足;
当时,或:
①若,则,解之得:;
②若,则,解之得:.
综上所述,的取值构成的集合为.
例8. 设集合,,若,则实数的取值范围是__________.
分析:先将并集运算的结果转化为两个集合M , N之间的关系,从而列出关于参数的不等式(组)求解.注意含参集合的分类讨论.
解:∵,∴.
分为两种情况:
①当时,有≥,解之得:≤;
②当时,则有:
,解之得:≤2.
综上所述,实数的取值范围是.
警示:在解决本题时,任意忽略的情况,另外要注意端点值能否取到.
例9. 已知集合,,若,求实数的取值范围.
分析:注意本题与例7的区别.
解:∵,∴.
分为三种情况:
①当时,恒成立,∴R,满足;
②当时,,有,解之得:
∴;
③当时,,有,解之得:
∴.
综上所述,实数的取值范围是.
题型二 交集运算
一般地,由属于集合A且属于集合B的所有元素组成的集合,称为集合A与集合B的交集,记作,读作“A交B”.
.
求交集的方法
(1)求两个有限集的交集 按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.(或可借助于Venn图)
(2)求两个无限集的交集 借助于数轴进行计算.两个集合的解集等于这两个集合在数轴上对应的图形所覆盖的公共范围.
例10. 设集合,集合,则【 】
(A) (B)
(C) (D)
分析:在进行集合的运算之前,要先弄清楚各个集合的本质.本题中集合A的代表元素为整数,所以集合A为范围内的整数集.
解:∵,
∴.
选择【 D 】.
例11. 设集合,,若,则实数的取值范围是__________.
分析:说明集合A、B有公共元素,在数轴上集合A、B所对应的图形覆盖的区域有公共部分.
解:.
例12. 设集合,,若,求实数的取值范围.
分析:若,则由交集的性质知,在得到这两个集合之间的关系后借助于数轴就可以列出不等式(组)进行求解了.
解:∵,∴.
分为两种情况:
①当时,满足,有≥,解之得:≤;
②当时,则有:
,解之得:≤2.
综上所述,实数的取值范围是.
★例13.(易错题)设集合,,则等于【 】
(A) (B)
(C) (D)
错解:解方程组得:或,故选【 C 】.
错因分析:这里好多学生认为是求抛物线和直线的交点坐标所构成的集合,根源在于没有搞清楚集合A , B的本质,没有弄清楚集合的代表元素的特征.
分析:本题中的两个集合都是由函数值构成的,它们的代表元素是函数值.表示函数和函数的函数值的交集.
解:∵,R.
∴R.
选择【 A 】.
变式: 设集合,,则等于【 】
(A) (B)
(C) (D)
例14. 已知集合,集合,则中元素的个数为【 】
(A)3 (B)2 (C)1 (D)0
解:解方程组得:
或
∴,共有2个元素.选择【 B 】.
方法二:由后面的学习可以知道,方程是单位圆的方程(以原点为圆心,以1为半径的圆).集合A是由圆上的所有点构成的,集合B是由直线上的所有点构成的,所以就是由单位圆与直线的交点构成的,如图所示,交点有两个,故中元素的个数为2.
例15.(2018沈阳重点高中)设集合,.
(1)若,求A的非空真子集的个数;
(2)若,求实数的取值范围.
分析:(1)子集、真子集个数的确定
若集合A含有个元素,则集合A:
(1)含有个子集;
(2)含有个非空子集;
(3)含有个真子集;
(4)含有个非空真子集.
(2)若,则,注意分类讨论.
解:(1)
∵集合A中含有8个元素
∴集合A的非空真子集的个数为;
(2)∵,∴.
分为两种情况:
①当时,满足,有,解之得:;
②当时,则有:
,解之得:≤≤3.
综上所述,实数的取值范围是.
例16. 设,,其中R,如果,求实数的取值范围.
解:
∵,∴
分为两种情况:
①当时,满足
∴,解之得:;
②当时,或或.
若或,则有,解之得:
经检验,此时;
若,则由根与系数的关系定理可得:
,解之得:.
综上所述,实数的取值范围是.
例17. 设集合,,若,求实数的取值范围.
分析:对于任意实数,都有,所以本题中集合A不会是空集.
解:∵,∴.
∵
∴,解之得:≤≤2.
∴实数的取值范围是.
★★例18.(综合性强)已知集合,集合,若:
(1)求实数的取值范围;
(2)当恒成立时,求的最小值.
分析:(1)求集合A时要解含参一元二次不等式,可借助于因式分解:
对于集合B,代表元素是,所以集合B是函数值的集合,通过配方得:
∵0≤≤3,∴2≤≤4,∴;
(2)这是与二次函数有关的恒成立问题,使用数形结合方法.
解:(1)
∵(这里作差比较与的大小)
∴
∴.
∵
∴,解之得:≤或≤≤2.
∴实数的取值范围是;
(2)∵恒成立,即≥0恒成立.
∴≤0,解之得:≤≤2.
∴的最小值为.
题型三 补集运算
全集 一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,记作U.
补集 对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集,简称集合A的补集,记作CU A,即
CU A.
补集的性质
①(CU A); ②(CU A); ③ CU (CU A);
④ CU U; ⑤ CU.
例19. 已知全集,集合,若CUA,则实数的取值范围是__________.
分析: CUA说明,且.
解:∵CUA,∴,且.
∴实数的取值范围是.
例20. 已知全集,集合,求CUA.
分析:集合A是由方程的解构成的,而方程可能无解、有两个不相等的实数根或有两个相等的实数根,需要分类讨论.
解:由题意可知:.
分为两种情况:
①当时,方程无实数根,∴,解之得:
∴CUACU;
②当时,则有≥0,解之得:≤或≥4.
设方程的两个实数根分别为
由根与系数的关系定理可得::
若,则,符合题意,此时,CUA;
若,则,符合题意,此时,CUA.
综上所述,当时,CUA;
当时,CUA;
当时,CUA.
例21. 已知,.
(1)当时,求;
(2)若CRA,求实数的取值范围.
分析:(1)求两个连续型实数集合的并集时,借助于数轴进行求解能将抽象的问题直观化,但要特别注意端点的实心和空心以及端点值的取舍;(2)求连续型实数集合的补集也是借助于数轴进行.
解:(1)当时,
∴;
(2)∵,∴CRA
∵CRA,∴分为两种情况:
①当时,有≥,解之得:≤;
②当时,则有:或
解之得:无解或.
综上,实数的取值范围是.
★例22. 设全集,,,求CIA.
解:
∴集合A是由直线上除点外的所有点构成的集合
∴CIA
∵
∴集合B是由直线上所有的点构成的集合
∴CIA.
附:函数,即的图象如图所示.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
