福建省晋江市季延中学2011-2012学年高二下学期期中考试数学(文)试题
文档属性
| 名称 | 福建省晋江市季延中学2011-2012学年高二下学期期中考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 233.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-03 00:00:00 | ||
图片预览


文档简介
(必修3,选修1-2,集合与简易逻辑)
试卷满分150分,考试时间120分钟
一、选择题(共12小题,每小题5分,共计60分)
1.若集合,,,那么()等于( )
A. B. C. D.
2.的共轭复数是( ).
A. B. C. D.
3.某校现有高一学生210人,高二学生270人,高三学生300人,学校学生会用分层抽样的方法从这三个年级的学生中抽取n个学生进行问卷调查,如果已知从高一学生中抽取的人数为7人,那么从高三学生中抽取的人数应为( ).
A.10 B.9 C.8 D.7
4.命题“存在,使”的否定是( )
A.存在,使 B.不存在,使
C.任意,使 D.任意,使
5.如果一组数中每个数减去同一个非零常数,则这一组数的( ).
A.平均数不变,方差不变 B.平均数改变,方差改变
C.平均数不变,方差改变 D.平均数改变,方差不变
6.已知p:|2x-3|>1 , q:>0,则是的( ).
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
7.按流程图的程序计算,若开始输入的值为,则输出的的值是( )
A. B. C. D.
8.在一次实验中,测得的四组值分别是,,,,
则与之间的回归直线方程为( ).
A. B. C. D.
9.在线性回归模型中,下列说法正确的是( ).
A.是一次函数;
B.因变量是由自变量唯一确定的;
C.因变量除了受自变量的影响外,可能还受到其它因素的影响;
这些因素会导致随机误差e的产生;
D.随机误差e是由于计算不准确造成的,可通过精确计算避免随机误差e的产生。
10.复数不是纯虚数,则有( ).
A. B. C.且 D.
11.已知集合,,且,
若,则( ).
A. B. C. D.
12.已知数列的前项和为,且,,可归纳猜想出的表达式为( ).
A. B. C. D.
二、填空题(共4小题,每小题4分,共计16分)
13.“若,则或”的否命题是__________________________.
14.设,则___________。
15.已知集合,若,则实数的取值范围是______________.
16.已知集合,对它的非空子集A,将A中每个元素k,都乘以再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对的所有非空子集,这些和的总和是 .
三、解答题(共6小题,共计74分)
17.已知复数,若,
⑴求; ⑵求实数的值.
18.已知集合A=,
且,求的值。
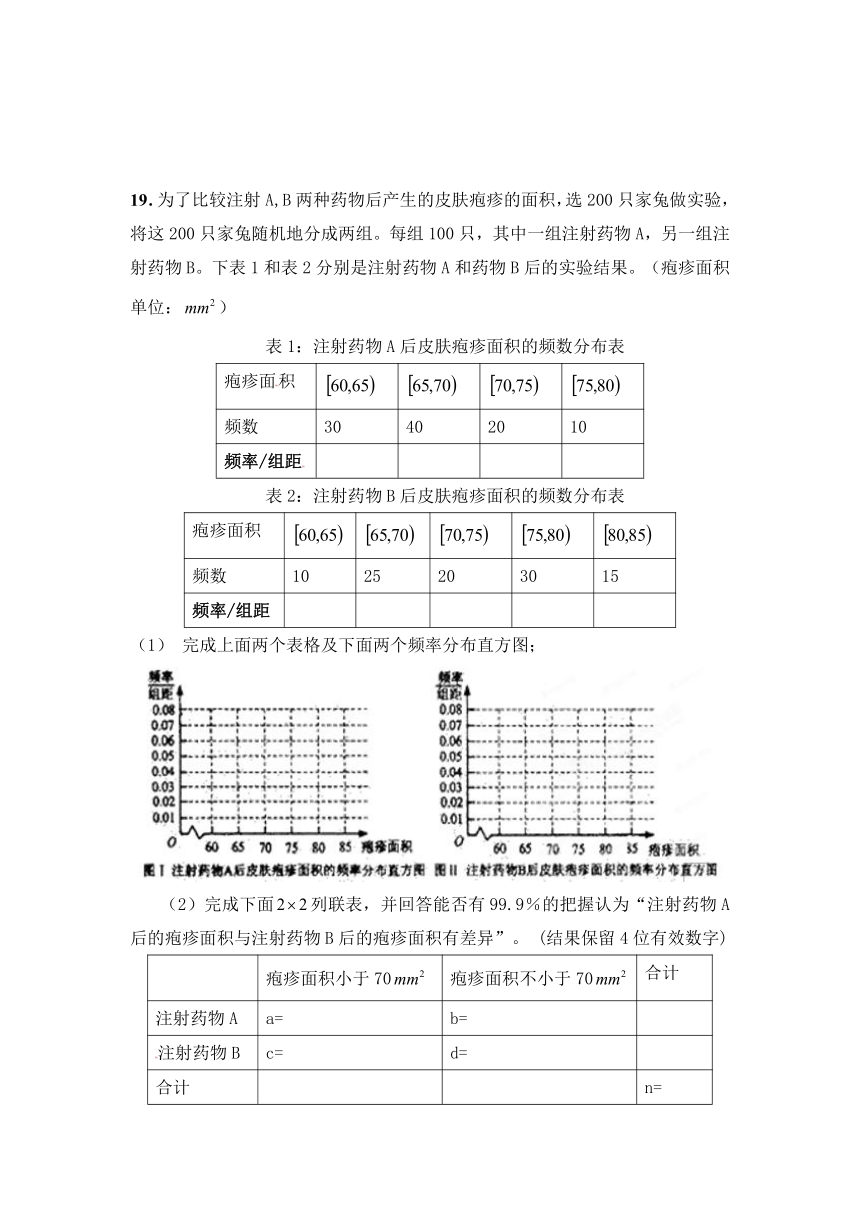
19.为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位:)
表1:注射药物A后皮肤疱疹面积的频数分布表
疱疹面积
频数 30 40 20 10
频率/组距
表2:注射药物B后皮肤疱疹面积的频数分布表
疱疹面积
频数 10 25 20 30 15
频率/组距
完成上面两个表格及下面两个频率分布直方图;
(2)完成下面列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
疱疹面积小于70 疱疹面积不小于70 合计
注射药物A a= b=
注射药物B c= d=
合计 n=
附:
P(K2≥k) 0.10 0.05 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
;
20.已知,设和是方程的两个根,不等式
对任意实数恒成立;函数有两个不同的零点.
求使“P且Q”为真命题的实数的取值范围.
21.适当方法证明:
(1)若,,求证:;
(2)已知,且, 求证:与中至少有一个小于2.
22.已知二次函数的二次项系数为,且不等式的解集为,
(1)若方程有两个相等的根,求的解析式;
(2)若的最大值为正数,求的取值范围.
季延中学 高二数学期中试卷(文科)
参考答案
选择题:(本大题共12小题,每小题5分,共60分)
二、填空题(本大题共4小题,每小题4分,共16分)
13.若,则且; 14.;
15. ; 16.2560;
三、解答题(共6小题,共计74分)
17.解:⑴
⑵,得 解得
19.解:
由于,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
20.解:由题设x1+x2=a,x1x2=-2,
∴|x1-x2|==.
当a∈[1,2]时,的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+=0的判别式
Δ=4m2-12(m+)=4m2-12m-16>0,
得m<-1或m>4.
综上,要使“P∧Q”为真命题,只需P真Q真,即
解得实数m的取值范围是(4,8].
22. 解:(1)∵f(x)+2x>0的解集为(1,3),
①
由方程,
②
∵方程②有两个相等的根,
∴,
即5a2-4a-1=0,解得a=1(舍) 或
代入①得:
(2)由
由 解得:
故当的最大值为正数时,实数a的取值范围是
输入x
计算 的值
输出结果x
是
否
试卷满分150分,考试时间120分钟
一、选择题(共12小题,每小题5分,共计60分)
1.若集合,,,那么()等于( )
A. B. C. D.
2.的共轭复数是( ).
A. B. C. D.
3.某校现有高一学生210人,高二学生270人,高三学生300人,学校学生会用分层抽样的方法从这三个年级的学生中抽取n个学生进行问卷调查,如果已知从高一学生中抽取的人数为7人,那么从高三学生中抽取的人数应为( ).
A.10 B.9 C.8 D.7
4.命题“存在,使”的否定是( )
A.存在,使 B.不存在,使
C.任意,使 D.任意,使
5.如果一组数中每个数减去同一个非零常数,则这一组数的( ).
A.平均数不变,方差不变 B.平均数改变,方差改变
C.平均数不变,方差改变 D.平均数改变,方差不变
6.已知p:|2x-3|>1 , q:>0,则是的( ).
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
7.按流程图的程序计算,若开始输入的值为,则输出的的值是( )
A. B. C. D.
8.在一次实验中,测得的四组值分别是,,,,
则与之间的回归直线方程为( ).
A. B. C. D.
9.在线性回归模型中,下列说法正确的是( ).
A.是一次函数;
B.因变量是由自变量唯一确定的;
C.因变量除了受自变量的影响外,可能还受到其它因素的影响;
这些因素会导致随机误差e的产生;
D.随机误差e是由于计算不准确造成的,可通过精确计算避免随机误差e的产生。
10.复数不是纯虚数,则有( ).
A. B. C.且 D.
11.已知集合,,且,
若,则( ).
A. B. C. D.
12.已知数列的前项和为,且,,可归纳猜想出的表达式为( ).
A. B. C. D.
二、填空题(共4小题,每小题4分,共计16分)
13.“若,则或”的否命题是__________________________.
14.设,则___________。
15.已知集合,若,则实数的取值范围是______________.
16.已知集合,对它的非空子集A,将A中每个元素k,都乘以再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对的所有非空子集,这些和的总和是 .
三、解答题(共6小题,共计74分)
17.已知复数,若,
⑴求; ⑵求实数的值.
18.已知集合A=,
且,求的值。
19.为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位:)
表1:注射药物A后皮肤疱疹面积的频数分布表
疱疹面积
频数 30 40 20 10
频率/组距
表2:注射药物B后皮肤疱疹面积的频数分布表
疱疹面积
频数 10 25 20 30 15
频率/组距
完成上面两个表格及下面两个频率分布直方图;
(2)完成下面列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
疱疹面积小于70 疱疹面积不小于70 合计
注射药物A a= b=
注射药物B c= d=
合计 n=
附:
P(K2≥k) 0.10 0.05 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
;
20.已知,设和是方程的两个根,不等式
对任意实数恒成立;函数有两个不同的零点.
求使“P且Q”为真命题的实数的取值范围.
21.适当方法证明:
(1)若,,求证:;
(2)已知,且, 求证:与中至少有一个小于2.
22.已知二次函数的二次项系数为,且不等式的解集为,
(1)若方程有两个相等的根,求的解析式;
(2)若的最大值为正数,求的取值范围.
季延中学 高二数学期中试卷(文科)
参考答案
选择题:(本大题共12小题,每小题5分,共60分)
二、填空题(本大题共4小题,每小题4分,共16分)
13.若,则且; 14.;
15. ; 16.2560;
三、解答题(共6小题,共计74分)
17.解:⑴
⑵,得 解得
19.解:
由于,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
20.解:由题设x1+x2=a,x1x2=-2,
∴|x1-x2|==.
当a∈[1,2]时,的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+=0的判别式
Δ=4m2-12(m+)=4m2-12m-16>0,
得m<-1或m>4.
综上,要使“P∧Q”为真命题,只需P真Q真,即
解得实数m的取值范围是(4,8].
22. 解:(1)∵f(x)+2x>0的解集为(1,3),
①
由方程,
②
∵方程②有两个相等的根,
∴,
即5a2-4a-1=0,解得a=1(舍) 或
代入①得:
(2)由
由 解得:
故当的最大值为正数时,实数a的取值范围是
输入x
计算 的值
输出结果x
是
否
同课章节目录
