2.3 简单的轴对称图形 课件(共43张PPT)
文档属性
| 名称 | 2.3 简单的轴对称图形 课件(共43张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 00:00:00 | ||
图片预览






文档简介
第二章 轴对称
3 简单的轴对称图形
知识点一 线段的轴对称性
1.线段的轴对称性戋段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
2.线段的垂直平分线:
温馨提示
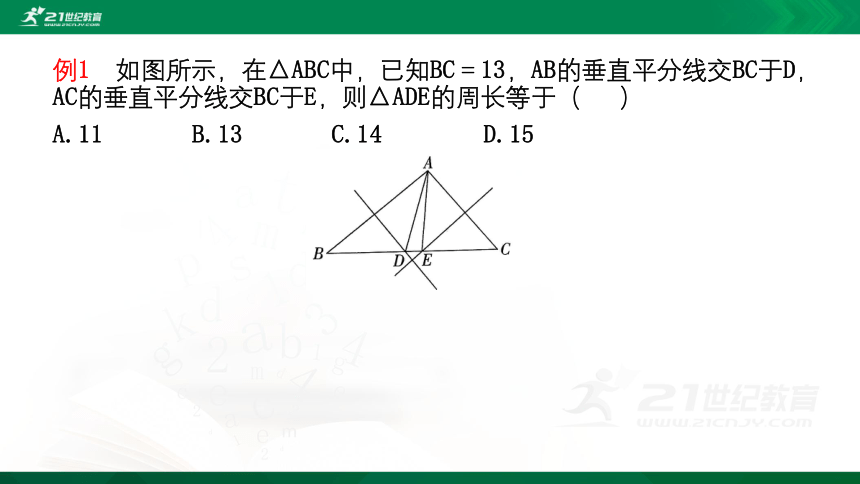
例1 如图所示,在△ABC中,已知BC=13,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则△ADE的周长等于( )
A.11 B.13 C.14 D.15
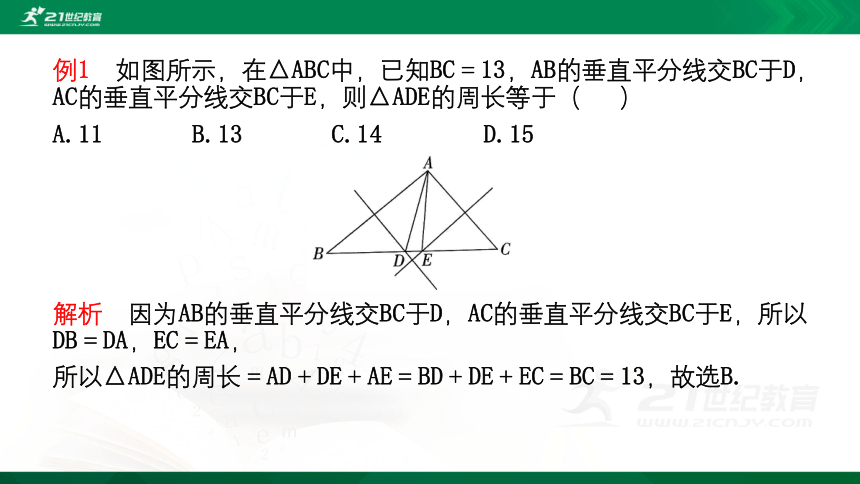
例1 如图所示,在△ABC中,已知BC=13,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则△ADE的周长等于( )
A.11 B.13 C.14 D.15
解析 因为AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,所以DB=DA,EC=EA,
所以△ADE的周长=AD+DE+AE=BD+DE+EC=BC=13,故选B.
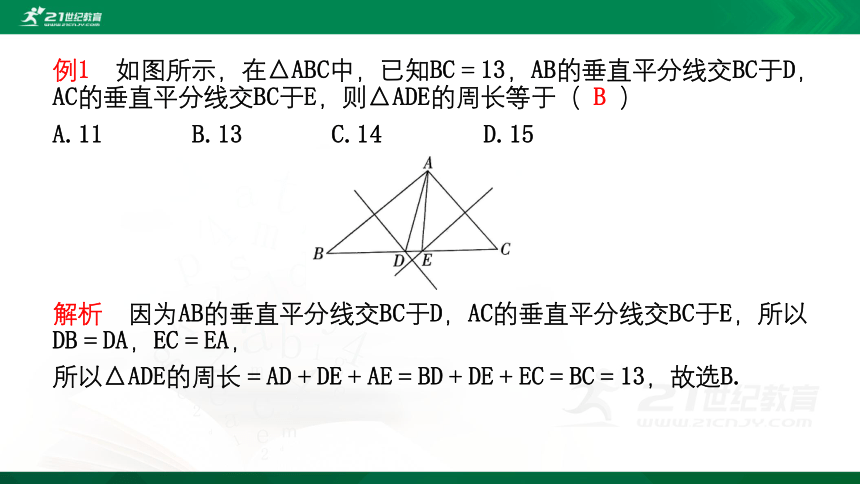
例1 如图所示,在△ABC中,已知BC=13,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则△ADE的周长等于( B )
A.11 B.13 C.14 D.15
解析 因为AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,所以DB=DA,EC=EA,
所以△ADE的周长=AD+DE+AE=BD+DE+EC=BC=13,故选B.
知识点二 角的轴对称性
1.角的轴对称性角是轴对称图形角平分线所在的直线是它的对称轴.
2.利用尺规作∠AOB的平分线:
3.角平分线的性质:
内容
符号语言
图形
角平分线的性质
角平分线上的点到角两边的距离相等
如果点P在∠AOB的平分线上,且P那么PD=PED⊥OA于点D,PE⊥OB于点E,
温馨提示
(1)性质中的距离是指点到角两边的垂线段的长.
(2)应用角平分线的性质解题的格式:
∵OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E,∴PD=PE.
(3)该性质是通过证明三角形全等得到的,它可以独立作为证明两条线段相等的依据,不必再证两个三角形全等.
(4)三角形的三条角平分线相交于一点,该点到三角形三边的距离相等.
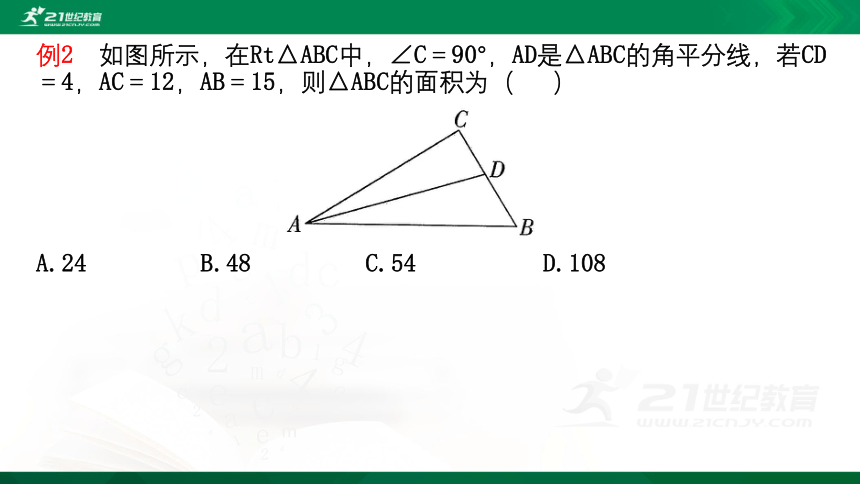
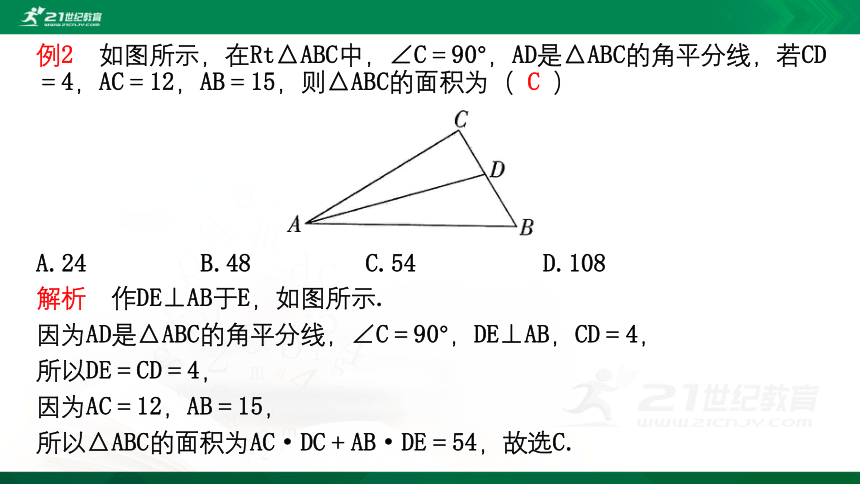
例2 如图所示,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,若CD=4,AC=12,AB=15,则△ABC的面积为( )
A.24 B.48 C.54 D.108
例2 如图所示,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,若CD=4,AC=12,AB=15,则△ABC的面积为( C )
A.24 B.48 C.54 D.108
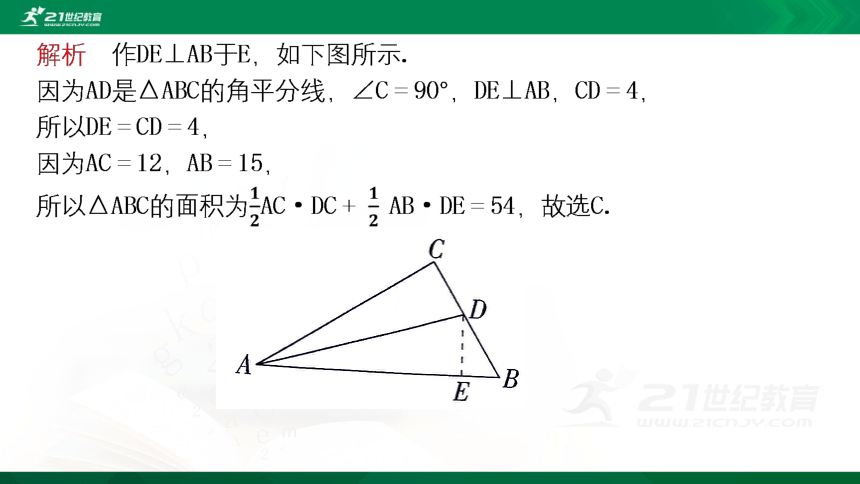
解析 作DE⊥AB于E,如图所示.
因为AD是△ABC的角平分线,∠C=90°,DE⊥AB,CD=4,
所以DE=CD=4,
因为AC=12,AB=15,
所以△ABC的面积为AC·DC+AB·DE=54,故选C.
知识点三 等腰三角形的性质及判定
内容
图形
知识详解
等腰三角形的性质
?
?
等腰三角形是轴对称图形
?
一般的等腰三角形(即不是等边三角形的等腰三角形)只有一条对称轴,顶角的平分线、底边上的高线、底边的中线所在的直线是它的对称轴
等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一)
?
?
?
?
?
?
(1)∵AB=AC, AD为BC边上的中线,∴AD⊥BC,且AD平分∠BAC;
(2)∵AB=AC,AD平分∠BAC,∴AD⊥BC,且BD=CD;(3)∵AB=AC,AD⊥BC,∴BD=CD,且AD平分∠BAC
三线合一包含了多层含义:
(1)等腰三角形底边的中线平分顶角且垂直于底边;
(2)等腰三角形顶角的平分线垂直平分底边;
(3)等腰三角形底边上的高线平分顶角、平分底边三线合一是证明角相等、线段相等或垂直的一个重要的方法.三线合一的前提条件是该三角形是等腰三角形
知识点三 等腰三角形的性质及判定
内容
图形
知识详解
等腰三角形的性质
?
等腰三角形两底角相等
?
?
?
?
?
在△ABC中,∵AB=AC,∴∠B=∠C.
?
(1)“等边对等角”只有在一个三角形中才能应用,若相等的线段不是同一个三角形的边,则不能应用该性质.
(2)依据三角形内角和定理可以由顶角求底角或由底角求顶角.
(3)这是等腰三角形的重要性质,它是证明角相等常用的方法,它的应用可省去三角形全等的证明,因此更简便
知识点三 等腰三角形的性质及判定
等腰三角形的判定方法
?
有两条边相等的三角形叫做等腰三角形
若AB=AC,
则△ABC是
等腰三角形
这是根据等腰三角形的定义进行判定的,任何一个图形的定义都是它的一个判定方法
如果一个三角形有两个角相等,那么它们所对的边也相等
在△ABC中,
∵∠B=∠C,
∴AB=AC
(等角对等边)
“等角对等边”应用比较广泛,我们往往通过计算三角形各角的度数,得到角相等,进而得到边相等.在运用时要找准“对边”与“对角”
例3 如图所示,在四边形ABCD中,AB=AD,∠ABC=∠ADC.试说明:BC=DC.
证明:连接BD,如右图所示,
∵AB=AD,∴∠ABD=∠ADB,
又∵∠ABC=∠ADC,
∴∠CBD=∠ABC-∠ABD,∠CDB=∠ADC-∠ADB,
∵∠CBD=∠CDB,∴BC=DC.
知识点四 等边三角形的性质定
1.等边三角形的性质
知识点四 等边三角形的性质定
1.等边三角形的性质
知识详解
(1)等边三角形每条边上的中线、高线和其对角的平分线“三线合一”,它们所在的直线就是等边三角形的对称轴.
(2)所有的等边三角形都是等腰三角形,但并不是所有的等腰三角形都是等边三角形.
知识点四 等边三角形的性质定
2.等边三角形的判定
知识点四 等边三角形的性质定
例4 如图所示,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
知识点四 等边三角形的性质定
例4 如图所示,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
证明:因为△ABC是等边三角形,
所以AB=AC=BC,∠ABC=∠ACB=∠CAB=60°,
因为DF⊥AB,DE⊥CB,EF⊥AC,
所以∠DAB=∠ACF=∠CBE=90°,所以∠FAC=∠BCE=∠DBA=30°,
所以∠D=∠E=∠F=180°-90°-30°=60°,所以△DEF是等边三角形.
知识点五 含有30°角的直角三角形的性质
例5 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AM平分∠BAC,AM的长为15cm,求BC的长.
经典例题
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
例1 如图所示,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,过点D作DE⊥AB于点E,点E恰为AB的中点,若DE=1,BD=2,求AC的长.
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
分析 AC可分为DC和DA两段,根据角平分线的性质可得DC=DE=1.根据线段垂直平分线的性质可得DA=DB=2.
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
分析 AC可分为DC和DA两段,根据角平分线的性质可得DC=DE=1.根据线段垂直平分线的性质可得DA=DB=2.
解析 因为BD平分∠ABC,∠C=90°,DE⊥AB,所以DC=DE=1.
因为DE⊥AB,E为AB的中点,所以DE垂直平分AB,所以DA=DB=2.
所以AC=DC+DA=1+2=3.
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
分析 AC可分为DC和DA两段,根据角平分线的性质可得DC=DE=1.根据线段垂直平分线的性质可得DA=DB=2.
解析 因为BD平分∠ABC,∠C=90°,DE⊥AB,所以DC=DE=1.
因为DE⊥AB,E为AB的中点,所以DE垂直平分AB,所以DA=DB=2.
所以AC=DC+DA=1+2=3.
点拨 角平分线的性质和线段垂直平分线的性质都是证明线段相等的重要方法,都比通过证明三角形全等得到线段相等简单.
题型二 含30°角的直角三角形性质的应用
题型二 含30°角的直角三角形性质的应用
题型二 含30°角的直角三角形性质的应用
易错易混
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
对于一个等腰三角形,若条件中没有明确指出角是顶角还是底角,或是没有明确指出哪条边是底边时,住往容易忽略掉分类讨论,从而导致漏解.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例1 已知等腰三角形中的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.50°或100°
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例1 已知等腰三角形中的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.50°或100°
解析 如图所示,△ABC中,AB=AC.
有两种情况:
①顶角∠A=50°;②底角是50°.
因为AB=AC,所以∠B=∠C=50°.
因为∠A+∠B+∠C=180°,所以∠A=180°-50°-50°=80°,
所以这个等腰三角形的顶角为50°和80°.
故选 C.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例1 已知等腰三角形中的一个内角为50°,则这个等腰三角形的顶角为( C )
A.50° B.80° C.50°或80° D.50°或100°
解析 如图所示,△ABC中,AB=AC.
有两种情况:
①顶角∠A=50°;②底角是50°.
因为AB=AC,所以∠B=∠C=50°.
因为∠A+∠B+∠C=180°,所以∠A=180°-50°-50°=80°,
所以这个等腰三角形的顶角为50°和80°.
故选 C.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
易错分析
注意此题分为两种情况:
(1)当顶角∠A=50°时,(2)当底角∠B=50°时.
解此题时易出现考虑问题不全面而漏解.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例2 如图所示,已知每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有( )
A.4个 B.5个 C.6个 D.7个
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
解析 如图所示,当AB为腰时,分别以A、B点为顶点,以AB为半径作圆,可找出6个点C.
故选C.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
易错分析
对于三角形的边AB是底还是腰,没有明确给出,需要分类讨论,讨论时要做到不重不漏.
3 简单的轴对称图形
知识点一 线段的轴对称性
1.线段的轴对称性戋段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
2.线段的垂直平分线:
温馨提示
例1 如图所示,在△ABC中,已知BC=13,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则△ADE的周长等于( )
A.11 B.13 C.14 D.15
例1 如图所示,在△ABC中,已知BC=13,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则△ADE的周长等于( )
A.11 B.13 C.14 D.15
解析 因为AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,所以DB=DA,EC=EA,
所以△ADE的周长=AD+DE+AE=BD+DE+EC=BC=13,故选B.
例1 如图所示,在△ABC中,已知BC=13,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则△ADE的周长等于( B )
A.11 B.13 C.14 D.15
解析 因为AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,所以DB=DA,EC=EA,
所以△ADE的周长=AD+DE+AE=BD+DE+EC=BC=13,故选B.
知识点二 角的轴对称性
1.角的轴对称性角是轴对称图形角平分线所在的直线是它的对称轴.
2.利用尺规作∠AOB的平分线:
3.角平分线的性质:
内容
符号语言
图形
角平分线的性质
角平分线上的点到角两边的距离相等
如果点P在∠AOB的平分线上,且P那么PD=PED⊥OA于点D,PE⊥OB于点E,
温馨提示
(1)性质中的距离是指点到角两边的垂线段的长.
(2)应用角平分线的性质解题的格式:
∵OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E,∴PD=PE.
(3)该性质是通过证明三角形全等得到的,它可以独立作为证明两条线段相等的依据,不必再证两个三角形全等.
(4)三角形的三条角平分线相交于一点,该点到三角形三边的距离相等.
例2 如图所示,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,若CD=4,AC=12,AB=15,则△ABC的面积为( )
A.24 B.48 C.54 D.108
例2 如图所示,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,若CD=4,AC=12,AB=15,则△ABC的面积为( C )
A.24 B.48 C.54 D.108
解析 作DE⊥AB于E,如图所示.
因为AD是△ABC的角平分线,∠C=90°,DE⊥AB,CD=4,
所以DE=CD=4,
因为AC=12,AB=15,
所以△ABC的面积为AC·DC+AB·DE=54,故选C.
知识点三 等腰三角形的性质及判定
内容
图形
知识详解
等腰三角形的性质
?
?
等腰三角形是轴对称图形
?
一般的等腰三角形(即不是等边三角形的等腰三角形)只有一条对称轴,顶角的平分线、底边上的高线、底边的中线所在的直线是它的对称轴
等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一)
?
?
?
?
?
?
(1)∵AB=AC, AD为BC边上的中线,∴AD⊥BC,且AD平分∠BAC;
(2)∵AB=AC,AD平分∠BAC,∴AD⊥BC,且BD=CD;(3)∵AB=AC,AD⊥BC,∴BD=CD,且AD平分∠BAC
三线合一包含了多层含义:
(1)等腰三角形底边的中线平分顶角且垂直于底边;
(2)等腰三角形顶角的平分线垂直平分底边;
(3)等腰三角形底边上的高线平分顶角、平分底边三线合一是证明角相等、线段相等或垂直的一个重要的方法.三线合一的前提条件是该三角形是等腰三角形
知识点三 等腰三角形的性质及判定
内容
图形
知识详解
等腰三角形的性质
?
等腰三角形两底角相等
?
?
?
?
?
在△ABC中,∵AB=AC,∴∠B=∠C.
?
(1)“等边对等角”只有在一个三角形中才能应用,若相等的线段不是同一个三角形的边,则不能应用该性质.
(2)依据三角形内角和定理可以由顶角求底角或由底角求顶角.
(3)这是等腰三角形的重要性质,它是证明角相等常用的方法,它的应用可省去三角形全等的证明,因此更简便
知识点三 等腰三角形的性质及判定
等腰三角形的判定方法
?
有两条边相等的三角形叫做等腰三角形
若AB=AC,
则△ABC是
等腰三角形
这是根据等腰三角形的定义进行判定的,任何一个图形的定义都是它的一个判定方法
如果一个三角形有两个角相等,那么它们所对的边也相等
在△ABC中,
∵∠B=∠C,
∴AB=AC
(等角对等边)
“等角对等边”应用比较广泛,我们往往通过计算三角形各角的度数,得到角相等,进而得到边相等.在运用时要找准“对边”与“对角”
例3 如图所示,在四边形ABCD中,AB=AD,∠ABC=∠ADC.试说明:BC=DC.
证明:连接BD,如右图所示,
∵AB=AD,∴∠ABD=∠ADB,
又∵∠ABC=∠ADC,
∴∠CBD=∠ABC-∠ABD,∠CDB=∠ADC-∠ADB,
∵∠CBD=∠CDB,∴BC=DC.
知识点四 等边三角形的性质定
1.等边三角形的性质
知识点四 等边三角形的性质定
1.等边三角形的性质
知识详解
(1)等边三角形每条边上的中线、高线和其对角的平分线“三线合一”,它们所在的直线就是等边三角形的对称轴.
(2)所有的等边三角形都是等腰三角形,但并不是所有的等腰三角形都是等边三角形.
知识点四 等边三角形的性质定
2.等边三角形的判定
知识点四 等边三角形的性质定
例4 如图所示,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
知识点四 等边三角形的性质定
例4 如图所示,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
证明:因为△ABC是等边三角形,
所以AB=AC=BC,∠ABC=∠ACB=∠CAB=60°,
因为DF⊥AB,DE⊥CB,EF⊥AC,
所以∠DAB=∠ACF=∠CBE=90°,所以∠FAC=∠BCE=∠DBA=30°,
所以∠D=∠E=∠F=180°-90°-30°=60°,所以△DEF是等边三角形.
知识点五 含有30°角的直角三角形的性质
例5 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AM平分∠BAC,AM的长为15cm,求BC的长.
经典例题
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
例1 如图所示,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,过点D作DE⊥AB于点E,点E恰为AB的中点,若DE=1,BD=2,求AC的长.
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
分析 AC可分为DC和DA两段,根据角平分线的性质可得DC=DE=1.根据线段垂直平分线的性质可得DA=DB=2.
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
分析 AC可分为DC和DA两段,根据角平分线的性质可得DC=DE=1.根据线段垂直平分线的性质可得DA=DB=2.
解析 因为BD平分∠ABC,∠C=90°,DE⊥AB,所以DC=DE=1.
因为DE⊥AB,E为AB的中点,所以DE垂直平分AB,所以DA=DB=2.
所以AC=DC+DA=1+2=3.
题型一 线段垂直平分线的性质与角平分线的性质的综合应用
分析 AC可分为DC和DA两段,根据角平分线的性质可得DC=DE=1.根据线段垂直平分线的性质可得DA=DB=2.
解析 因为BD平分∠ABC,∠C=90°,DE⊥AB,所以DC=DE=1.
因为DE⊥AB,E为AB的中点,所以DE垂直平分AB,所以DA=DB=2.
所以AC=DC+DA=1+2=3.
点拨 角平分线的性质和线段垂直平分线的性质都是证明线段相等的重要方法,都比通过证明三角形全等得到线段相等简单.
题型二 含30°角的直角三角形性质的应用
题型二 含30°角的直角三角形性质的应用
题型二 含30°角的直角三角形性质的应用
易错易混
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
对于一个等腰三角形,若条件中没有明确指出角是顶角还是底角,或是没有明确指出哪条边是底边时,住往容易忽略掉分类讨论,从而导致漏解.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例1 已知等腰三角形中的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.50°或100°
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例1 已知等腰三角形中的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.50°或100°
解析 如图所示,△ABC中,AB=AC.
有两种情况:
①顶角∠A=50°;②底角是50°.
因为AB=AC,所以∠B=∠C=50°.
因为∠A+∠B+∠C=180°,所以∠A=180°-50°-50°=80°,
所以这个等腰三角形的顶角为50°和80°.
故选 C.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例1 已知等腰三角形中的一个内角为50°,则这个等腰三角形的顶角为( C )
A.50° B.80° C.50°或80° D.50°或100°
解析 如图所示,△ABC中,AB=AC.
有两种情况:
①顶角∠A=50°;②底角是50°.
因为AB=AC,所以∠B=∠C=50°.
因为∠A+∠B+∠C=180°,所以∠A=180°-50°-50°=80°,
所以这个等腰三角形的顶角为50°和80°.
故选 C.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
易错分析
注意此题分为两种情况:
(1)当顶角∠A=50°时,(2)当底角∠B=50°时.
解此题时易出现考虑问题不全面而漏解.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
例2 如图所示,已知每个小方格的边长为1,A,B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是以AB为腰的等腰三角形,这样的格点C有( )
A.4个 B.5个 C.6个 D.7个
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
解析 如图所示,当AB为腰时,分别以A、B点为顶点,以AB为半径作圆,可找出6个点C.
故选C.
易错点 等腰三角形顶角、底角或腰、底边不明确时,考虑不周导致漏解
易错分析
对于三角形的边AB是底还是腰,没有明确给出,需要分类讨论,讨论时要做到不重不漏.
