人教版2021年九年级上册21.3《实际问题与一元二次方程》同步练习 (word解析版)
文档属性
| 名称 | 人教版2021年九年级上册21.3《实际问题与一元二次方程》同步练习 (word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 97.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 00:00:00 | ||
图片预览



文档简介
人教版2021年九年级上册21.3《实际问题与一元二次方程》同步练习
一.选择题
1.用一条长60cm的绳子怎样围成一个面积为200cm2的矩形?设矩形的一边为xcm,根据题意,可列方程为( )
A.x(30+x)=200 B.x(30﹣x)=200
C.x(x+60)=200 D.x(60﹣x)=200
2.学校初二年级组织足球联赛,赛制为单循环制(每两个队之间比赛一场).共进行了28场比赛,问初二年级有几个参赛班级?设初二年级有x个班级参加比赛.根据题意列出方程正确的是( )
A.x2=28 B.x(x﹣1)=28
C.x2=28 D.x(x﹣1)=28
3.某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )
A.800(1﹣x)2=968 B.800(1+x)2=968
C.968(1﹣x)2=800 D.968(1+x)2=800
4.如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,各彩条的宽度相等,如果要使彩条所占面积是图案面积的六分之一.设彩条的宽为xcm,根据题意可列方程( )
A.(20﹣2x)(30﹣2x)=20×30×
B.(20﹣2x)(30﹣2x)=20×30×(1﹣)
C.(20﹣x)(30﹣x)=20×30×
D.(20﹣x)(30﹣x)=20×30×(1﹣)
5.有1人患了流感,经过两轮传染后共有81人患了流感,设每轮传染中每人传染x人,其中20%的人因自身抵抗力强而未患流感,则根据题意可列方程为( )
A.0.2(1+x)2=81 B.(1+0.2x)2=81
C.0.8(1+x)2=81 D.(1+0.8x)2=81
6.某厂家2021年1﹣5月份的产量如图所示.下面有三个推断:
①从1月份到5月份产量在逐月增长;②1月份到2月份产量的增长率是60%;③若设从3月份到5月份产量的平均月增长率为x,则可列方程为220(1+x)2=480.所有正确的推断是( )
A.② B.③ C.①② D.②③
7.一个直角三角形的两条直角边的和是14cm,面积是24cm2,则其斜边长为( )
A.2cm B.10cm C.8cm D.4cm
8.元旦来临前,某商场将一件原价为a元的衬衫以一个给定的百分比提升价格,元旦那天商场又按照新的价格以相同的百分比降低了这件衬衫的价格,最终,衬衫的价格比原价降低了0.16a元,则这个给定的百分比为( )
A.16% B.36% C.40% D.50%
9.日前以5G等为代表的战略性新兴产业蓬勃发展,某市2019年底有5G用户2万户,计划到2021年底全市5G用户数累计达到8.72万户,设全市5G用户数年平均增长率为x.则x值为( )
A.20% B.30% C.40% D.50%
10.如图,在长为32m,宽为20m的长方形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,则道路的宽( )m.
A.1 B.1.5 C.2 D.2.5
二.填空题
11.2021年元旦联欢会上,某班同学之间互赠新年贺卡,共赠贺卡1190张,设全班有x名同学,则可列方程为 .
12.某种商品原价每件售价为400元,经过连续两次降价后,每件售价为288元,设平均每次降价的百分率为x,则可列方程为 .
13.秋冬季节为流感的高发期,有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染的人数为 .
14.一个两位数,十位上的数字比个位上的数字的平方小3,如果把这个数的个位数字与十位数字交换,那么所得到的两位数比原来的数小27,则原来的两位数是 .
15.2021年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价x元,可列方程 .
16.哈尔滨市某楼盘以每平方米10000元的均价对外销售,经过连续两次降价后,均价为每平方米8100元,则平均每次降价的百分率为 .
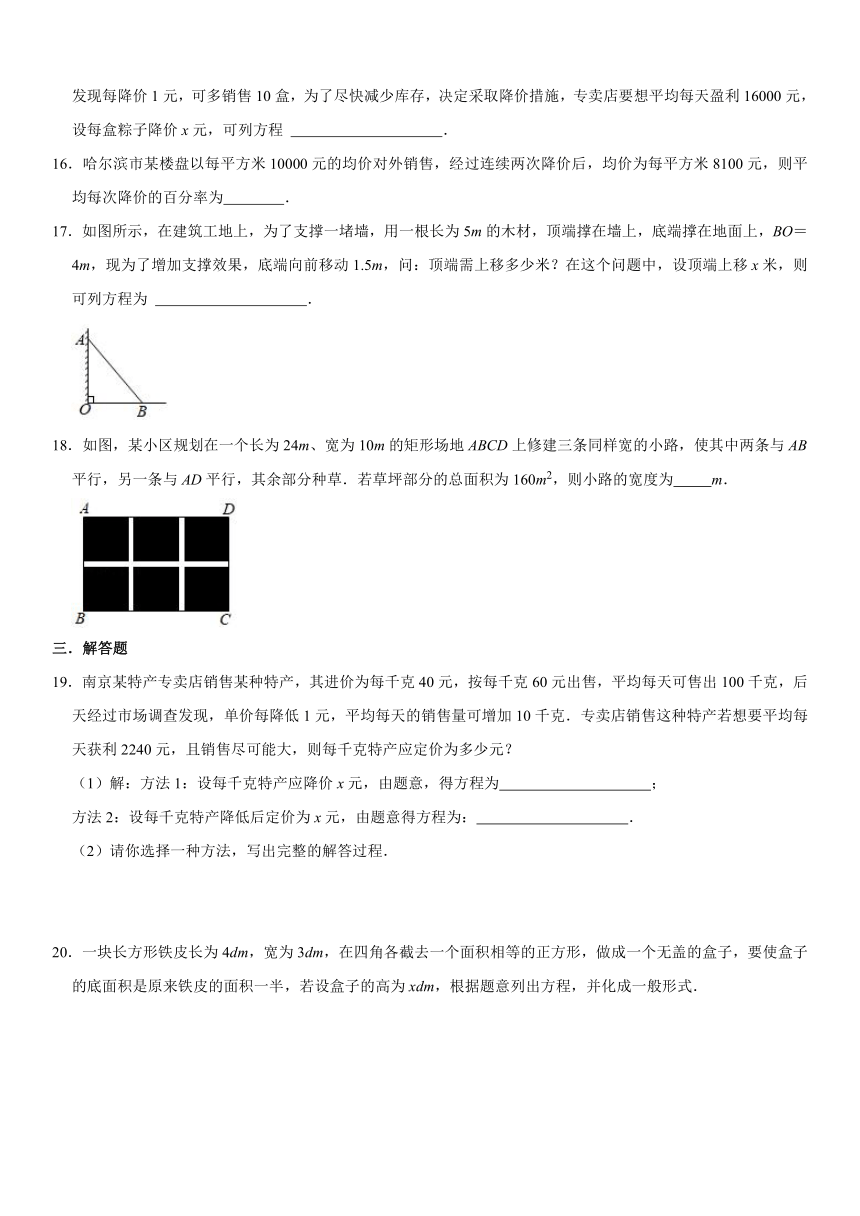
17.如图所示,在建筑工地上,为了支撑一堵墙,用一根长为5m的木材,顶端撑在墙上,底端撑在地面上,BO=4m,现为了增加支撑效果,底端向前移动1.5m,问:顶端需上移多少米?在这个问题中,设顶端上移x米,则可列方程为 .
18.如图,某小区规划在一个长为24m、宽为10m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分的总面积为160m2,则小路的宽度为 m.
三.解答题
19.南京某特产专卖店销售某种特产,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后天经过市场调查发现,单价每降低1元,平均每天的销售量可增加10千克.专卖店销售这种特产若想要平均每天获利2240元,且销售尽可能大,则每千克特产应定价为多少元?
(1)解:方法1:设每千克特产应降价x元,由题意,得方程为 ;
方法2:设每千克特产降低后定价为x元,由题意得方程为: .
(2)请你选择一种方法,写出完整的解答过程.
20.一块长方形铁皮长为4dm,宽为3dm,在四角各截去一个面积相等的正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积一半,若设盒子的高为xdm,根据题意列出方程,并化成一般形式.
21.一个QQ群里共有x个好友,每个好友都分别给其他好友发了一条消息,这样一共产生756条消息
(1)列出关于x的方程;
(2)将方程化为ax2+bx+c=0的形式,并指出a,b,c的值.
22.2020年1月底,武汉爆发“新冠”疫情后,口罩成为家庭必需品,某口罩经销商批发了一批口罩,进货单价为每盒50元,若按每盒60元出售,则可销售80盒.现准备提价销售,经市场调研发现:每盒每提价1元,销量就会减少2盒,为保护消费者利益,物价部门规定,销售利润不能超过50%,设该口罩售价为每盒x(x>60)元.
(1)用含x的代数式表示提价后平均每天的销售量为 盒;
(2)现在预算要获得1200元利润,应按每盒多少元销售?
23.某租赁公司有房屋100套.据统计,当每套房屋的月租金为3000元时,可全部租出.每套房屋的月租金每增加50元,租出的房屋数将减少1套.
(1)当每套房屋的月租金定为3500元时,能租出多少套?
(2)当每套房屋的月租金定价为多少元时,租赁公司的月租金可达到315000元?
24.“杂交水稻之父”﹣﹣袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.
参考答案
一.选择题
1.解:设矩形的一边为x米,
∵长方形的周长为60cm,
∴矩形的另一边=(30﹣x)(cm),
得x(30﹣x)=200.
故选:B.
2.解:设这次有x队参加比赛,则此次比赛的总场数为:x(x﹣1)场,
根据题意列出方程得:x(x﹣1)=28,
故选:B.
3.解:依题意得:800(1+x)2=968.
故选:B.
4.解:设彩条的宽度是xcm,则
(20﹣2x)(30﹣2x)=×20×30,
故选:B.
5.解:依题意得(1+0.8x)2=81,
故选:D.
6.解:①∵220<240,
∴3月份的产量比2月份的产量低,推论①不正确;
②∵×100%=60%,
∴1月份到2月份产量的增长率是60%,推论②正确;
③设从3月份到5月份产量的平均月增长率为x,
依题意得:220(1+x)2=480,推论③正确.
故选:D.
7.解:设这个直角三角形的两直角边为a、b,斜边为c,
根据题意得a+b=14,ab=24,即ab=48,
∴c2=a2+b2=(a+b)2﹣2ab=142﹣2×48=100,
开平方,得c=10,即斜边长为10cm.
故选:B.
8.解:设这个给定的百分比为x,根据题意得,
a(1+x)(1﹣x)=a﹣0.16a,
解得x1=0.4,x2=﹣0.4(舍去),
即这个给定的百分比为40%.
故选:C.
9.解:设全市5G用户数年平均增长率为x,则2020年底有5G用户2(1+x)万户,2021年底有5G用户2(1+x)2万户,
依题意得:2+2(1+x)+2(1+x)2=8.72,
整理得:x2+3x﹣1.36=0,
解得:x1=0.4=40%,x2=﹣3.4(不合题意,舍去).
故选:C.
10.解:原图经过平移转化为图1.
设道路宽为xm,
根据题意,得(20﹣x)(32﹣x)=540.
整理得x2﹣52x+100=0.
解得x1=50(不合题意,舍去),x2=2.
则道路宽为2m,
故选:C.
二.填空题
11.解:由题意可得,
x(x﹣1)=1190,
故答案为:x(x﹣1)=1190.
12.解:设平均每次降价的百分率为x,
依题意得:400(1﹣x)2=288.
故答案为:400(1﹣x)2=288.
13.解:设每轮传染中平均一个人传染的人数为x人,
依题意得:(1+x)2=121,
解得:x1=10,x2=﹣12(不合题意,舍去).
故答案为:10人.
14.解:设这个数的个位数字为x,则十位数字为(x+)=(x+3),
依题意得:x2﹣(x+)=3,
整理得:x2﹣x﹣6=0,
解得:x1=3,x2=﹣2,
又∵x为非负整数,
∴x=3,
∴10(x+)+x=63.
故答案为:63.
15.解:设每盒粽子降价x元,则每盒的利润为(50﹣x)元,平均每天可卖(300+10x)盒,
依题意得:(50﹣x)(300+10x)=16000,
故答案为:(50﹣x)(300+10x)=16000.
16.解:设平均每次降价的百分率为x,
依题意得:10000(1﹣x)2=8100,
解得:x1=0.1=10%,x2=1.9(不合题意,舍去).
故答案为:10%.
17.解:在△AOB中,∠AOB=90°,BO=4,AB=5,
∴AO==3.
设顶端上移x米,
依题意得:(x+3)2+(4﹣1.5)2=52.
故答案为:(x+3)2+(4﹣1.5)2=52.
18.解:如图,设修建的小路宽应为x米,
则新的草坪面积等于矩形DEFG的面积,
即得到方程:(24﹣2x)×(10﹣x)=160,
整理得:x2﹣22x+40=0,解得x=20或x=2.
但x=20不合题意,舍去,
所以修建的小路宽应为2米.
故答案为:2.
三.解答题
19.解:(1)方法1:设每千克特产应降价x元. 根据题意,得
(60﹣x﹣40)(100+10x)=2240.
方法2:设每千克特产降价后定价为x元,由题意,得
(x﹣40)[100+10(60﹣x)]=2240,
故答案为:(60﹣x﹣40)(100+10x)=2240,(x﹣40)[100+10(60﹣x)]=2240;
(2)方法1:设每千克特产应降价x元. 根据题意,得
(60﹣x﹣40)(100+10x)=2240,
解得x1=4,x2=6.
要让顾客尽可能得到实惠,只能取x=6,
60﹣6=54元,
答:每千克特产应定价54元.
方法2:设每千克特产降价后定价为x元,由题意,得
(x﹣40)[100+10(60﹣x)]=2240
解得x1=54,x2=56.
要让顾客尽可能得到实惠,只能取x=54,
答:每千克特产应定价54元.
20.解:由题意得:无盖长方体盒子的底面长为(4﹣2x)dm,宽为(3﹣2x)dm,由题意得,
(4﹣2x)(3﹣2x)=4×3×,
整理得:2x2﹣7x+3=0,
21.解:(1)由题意可得:x(x﹣1)=756;
(2)x(x﹣1)=756
整理得:x2﹣x﹣756=0,
则a=1,b=﹣1,c=﹣756.
22.解:(1)根据题意,提价后平均每天的销售量为:80﹣2(x﹣60)=200﹣2x.
故答案是:(200﹣2x);
(2)根据题意得:(x﹣50)(200﹣2x)=1200,
整理得:x2﹣150x+5600=0.
解得:x1=70,x2=80.
当x=70时,利润率=,符合题意;
当x=80时,利润率=,不合题意,舍去.
所以要获得1200元利润,应按70元每盒销售.
23.解:(1)100﹣=90(套).
答:当每套房屋的月租金定为3500元时,能租出90套.
(2)设每套房屋的月租金定价为x元,则可租出(100﹣)套房屋,
依题意得:x(100﹣)=315000,
整理得:x2﹣8000x+15750000=0,
解得:x1=4500,x2=3500.
答:当每套房屋的月租金定价为4500元或3500元时,租赁公司的月租金可达到315000元.
24.解:(1)设亩产量的平均增长率为x,
依题意得:700(1+x)2=1008,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:亩产量的平均增长率为20%.
(2)1008×(1+20%)=1209.6(公斤).
∵1209.6>1200,
∴他们的目标能实现.
一.选择题
1.用一条长60cm的绳子怎样围成一个面积为200cm2的矩形?设矩形的一边为xcm,根据题意,可列方程为( )
A.x(30+x)=200 B.x(30﹣x)=200
C.x(x+60)=200 D.x(60﹣x)=200
2.学校初二年级组织足球联赛,赛制为单循环制(每两个队之间比赛一场).共进行了28场比赛,问初二年级有几个参赛班级?设初二年级有x个班级参加比赛.根据题意列出方程正确的是( )
A.x2=28 B.x(x﹣1)=28
C.x2=28 D.x(x﹣1)=28
3.某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )
A.800(1﹣x)2=968 B.800(1+x)2=968
C.968(1﹣x)2=800 D.968(1+x)2=800
4.如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,各彩条的宽度相等,如果要使彩条所占面积是图案面积的六分之一.设彩条的宽为xcm,根据题意可列方程( )
A.(20﹣2x)(30﹣2x)=20×30×
B.(20﹣2x)(30﹣2x)=20×30×(1﹣)
C.(20﹣x)(30﹣x)=20×30×
D.(20﹣x)(30﹣x)=20×30×(1﹣)
5.有1人患了流感,经过两轮传染后共有81人患了流感,设每轮传染中每人传染x人,其中20%的人因自身抵抗力强而未患流感,则根据题意可列方程为( )
A.0.2(1+x)2=81 B.(1+0.2x)2=81
C.0.8(1+x)2=81 D.(1+0.8x)2=81
6.某厂家2021年1﹣5月份的产量如图所示.下面有三个推断:
①从1月份到5月份产量在逐月增长;②1月份到2月份产量的增长率是60%;③若设从3月份到5月份产量的平均月增长率为x,则可列方程为220(1+x)2=480.所有正确的推断是( )
A.② B.③ C.①② D.②③
7.一个直角三角形的两条直角边的和是14cm,面积是24cm2,则其斜边长为( )
A.2cm B.10cm C.8cm D.4cm
8.元旦来临前,某商场将一件原价为a元的衬衫以一个给定的百分比提升价格,元旦那天商场又按照新的价格以相同的百分比降低了这件衬衫的价格,最终,衬衫的价格比原价降低了0.16a元,则这个给定的百分比为( )
A.16% B.36% C.40% D.50%
9.日前以5G等为代表的战略性新兴产业蓬勃发展,某市2019年底有5G用户2万户,计划到2021年底全市5G用户数累计达到8.72万户,设全市5G用户数年平均增长率为x.则x值为( )
A.20% B.30% C.40% D.50%
10.如图,在长为32m,宽为20m的长方形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,则道路的宽( )m.
A.1 B.1.5 C.2 D.2.5
二.填空题
11.2021年元旦联欢会上,某班同学之间互赠新年贺卡,共赠贺卡1190张,设全班有x名同学,则可列方程为 .
12.某种商品原价每件售价为400元,经过连续两次降价后,每件售价为288元,设平均每次降价的百分率为x,则可列方程为 .
13.秋冬季节为流感的高发期,有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染的人数为 .
14.一个两位数,十位上的数字比个位上的数字的平方小3,如果把这个数的个位数字与十位数字交换,那么所得到的两位数比原来的数小27,则原来的两位数是 .
15.2021年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价x元,可列方程 .
16.哈尔滨市某楼盘以每平方米10000元的均价对外销售,经过连续两次降价后,均价为每平方米8100元,则平均每次降价的百分率为 .
17.如图所示,在建筑工地上,为了支撑一堵墙,用一根长为5m的木材,顶端撑在墙上,底端撑在地面上,BO=4m,现为了增加支撑效果,底端向前移动1.5m,问:顶端需上移多少米?在这个问题中,设顶端上移x米,则可列方程为 .
18.如图,某小区规划在一个长为24m、宽为10m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若草坪部分的总面积为160m2,则小路的宽度为 m.
三.解答题
19.南京某特产专卖店销售某种特产,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后天经过市场调查发现,单价每降低1元,平均每天的销售量可增加10千克.专卖店销售这种特产若想要平均每天获利2240元,且销售尽可能大,则每千克特产应定价为多少元?
(1)解:方法1:设每千克特产应降价x元,由题意,得方程为 ;
方法2:设每千克特产降低后定价为x元,由题意得方程为: .
(2)请你选择一种方法,写出完整的解答过程.
20.一块长方形铁皮长为4dm,宽为3dm,在四角各截去一个面积相等的正方形,做成一个无盖的盒子,要使盒子的底面积是原来铁皮的面积一半,若设盒子的高为xdm,根据题意列出方程,并化成一般形式.
21.一个QQ群里共有x个好友,每个好友都分别给其他好友发了一条消息,这样一共产生756条消息
(1)列出关于x的方程;
(2)将方程化为ax2+bx+c=0的形式,并指出a,b,c的值.
22.2020年1月底,武汉爆发“新冠”疫情后,口罩成为家庭必需品,某口罩经销商批发了一批口罩,进货单价为每盒50元,若按每盒60元出售,则可销售80盒.现准备提价销售,经市场调研发现:每盒每提价1元,销量就会减少2盒,为保护消费者利益,物价部门规定,销售利润不能超过50%,设该口罩售价为每盒x(x>60)元.
(1)用含x的代数式表示提价后平均每天的销售量为 盒;
(2)现在预算要获得1200元利润,应按每盒多少元销售?
23.某租赁公司有房屋100套.据统计,当每套房屋的月租金为3000元时,可全部租出.每套房屋的月租金每增加50元,租出的房屋数将减少1套.
(1)当每套房屋的月租金定为3500元时,能租出多少套?
(2)当每套房屋的月租金定价为多少元时,租赁公司的月租金可达到315000元?
24.“杂交水稻之父”﹣﹣袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.
参考答案
一.选择题
1.解:设矩形的一边为x米,
∵长方形的周长为60cm,
∴矩形的另一边=(30﹣x)(cm),
得x(30﹣x)=200.
故选:B.
2.解:设这次有x队参加比赛,则此次比赛的总场数为:x(x﹣1)场,
根据题意列出方程得:x(x﹣1)=28,
故选:B.
3.解:依题意得:800(1+x)2=968.
故选:B.
4.解:设彩条的宽度是xcm,则
(20﹣2x)(30﹣2x)=×20×30,
故选:B.
5.解:依题意得(1+0.8x)2=81,
故选:D.
6.解:①∵220<240,
∴3月份的产量比2月份的产量低,推论①不正确;
②∵×100%=60%,
∴1月份到2月份产量的增长率是60%,推论②正确;
③设从3月份到5月份产量的平均月增长率为x,
依题意得:220(1+x)2=480,推论③正确.
故选:D.
7.解:设这个直角三角形的两直角边为a、b,斜边为c,
根据题意得a+b=14,ab=24,即ab=48,
∴c2=a2+b2=(a+b)2﹣2ab=142﹣2×48=100,
开平方,得c=10,即斜边长为10cm.
故选:B.
8.解:设这个给定的百分比为x,根据题意得,
a(1+x)(1﹣x)=a﹣0.16a,
解得x1=0.4,x2=﹣0.4(舍去),
即这个给定的百分比为40%.
故选:C.
9.解:设全市5G用户数年平均增长率为x,则2020年底有5G用户2(1+x)万户,2021年底有5G用户2(1+x)2万户,
依题意得:2+2(1+x)+2(1+x)2=8.72,
整理得:x2+3x﹣1.36=0,
解得:x1=0.4=40%,x2=﹣3.4(不合题意,舍去).
故选:C.
10.解:原图经过平移转化为图1.
设道路宽为xm,
根据题意,得(20﹣x)(32﹣x)=540.
整理得x2﹣52x+100=0.
解得x1=50(不合题意,舍去),x2=2.
则道路宽为2m,
故选:C.
二.填空题
11.解:由题意可得,
x(x﹣1)=1190,
故答案为:x(x﹣1)=1190.
12.解:设平均每次降价的百分率为x,
依题意得:400(1﹣x)2=288.
故答案为:400(1﹣x)2=288.
13.解:设每轮传染中平均一个人传染的人数为x人,
依题意得:(1+x)2=121,
解得:x1=10,x2=﹣12(不合题意,舍去).
故答案为:10人.
14.解:设这个数的个位数字为x,则十位数字为(x+)=(x+3),
依题意得:x2﹣(x+)=3,
整理得:x2﹣x﹣6=0,
解得:x1=3,x2=﹣2,
又∵x为非负整数,
∴x=3,
∴10(x+)+x=63.
故答案为:63.
15.解:设每盒粽子降价x元,则每盒的利润为(50﹣x)元,平均每天可卖(300+10x)盒,
依题意得:(50﹣x)(300+10x)=16000,
故答案为:(50﹣x)(300+10x)=16000.
16.解:设平均每次降价的百分率为x,
依题意得:10000(1﹣x)2=8100,
解得:x1=0.1=10%,x2=1.9(不合题意,舍去).
故答案为:10%.
17.解:在△AOB中,∠AOB=90°,BO=4,AB=5,
∴AO==3.
设顶端上移x米,
依题意得:(x+3)2+(4﹣1.5)2=52.
故答案为:(x+3)2+(4﹣1.5)2=52.
18.解:如图,设修建的小路宽应为x米,
则新的草坪面积等于矩形DEFG的面积,
即得到方程:(24﹣2x)×(10﹣x)=160,
整理得:x2﹣22x+40=0,解得x=20或x=2.
但x=20不合题意,舍去,
所以修建的小路宽应为2米.
故答案为:2.
三.解答题
19.解:(1)方法1:设每千克特产应降价x元. 根据题意,得
(60﹣x﹣40)(100+10x)=2240.
方法2:设每千克特产降价后定价为x元,由题意,得
(x﹣40)[100+10(60﹣x)]=2240,
故答案为:(60﹣x﹣40)(100+10x)=2240,(x﹣40)[100+10(60﹣x)]=2240;
(2)方法1:设每千克特产应降价x元. 根据题意,得
(60﹣x﹣40)(100+10x)=2240,
解得x1=4,x2=6.
要让顾客尽可能得到实惠,只能取x=6,
60﹣6=54元,
答:每千克特产应定价54元.
方法2:设每千克特产降价后定价为x元,由题意,得
(x﹣40)[100+10(60﹣x)]=2240
解得x1=54,x2=56.
要让顾客尽可能得到实惠,只能取x=54,
答:每千克特产应定价54元.
20.解:由题意得:无盖长方体盒子的底面长为(4﹣2x)dm,宽为(3﹣2x)dm,由题意得,
(4﹣2x)(3﹣2x)=4×3×,
整理得:2x2﹣7x+3=0,
21.解:(1)由题意可得:x(x﹣1)=756;
(2)x(x﹣1)=756
整理得:x2﹣x﹣756=0,
则a=1,b=﹣1,c=﹣756.
22.解:(1)根据题意,提价后平均每天的销售量为:80﹣2(x﹣60)=200﹣2x.
故答案是:(200﹣2x);
(2)根据题意得:(x﹣50)(200﹣2x)=1200,
整理得:x2﹣150x+5600=0.
解得:x1=70,x2=80.
当x=70时,利润率=,符合题意;
当x=80时,利润率=,不合题意,舍去.
所以要获得1200元利润,应按70元每盒销售.
23.解:(1)100﹣=90(套).
答:当每套房屋的月租金定为3500元时,能租出90套.
(2)设每套房屋的月租金定价为x元,则可租出(100﹣)套房屋,
依题意得:x(100﹣)=315000,
整理得:x2﹣8000x+15750000=0,
解得:x1=4500,x2=3500.
答:当每套房屋的月租金定价为4500元或3500元时,租赁公司的月租金可达到315000元.
24.解:(1)设亩产量的平均增长率为x,
依题意得:700(1+x)2=1008,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:亩产量的平均增长率为20%.
(2)1008×(1+20%)=1209.6(公斤).
∵1209.6>1200,
∴他们的目标能实现.
同课章节目录
