湖南省长沙市2020-2021学年八年级下学期期末联考数学试卷(word版,含答案)
文档属性
| 名称 | 湖南省长沙市2020-2021学年八年级下学期期末联考数学试卷(word版,含答案) | 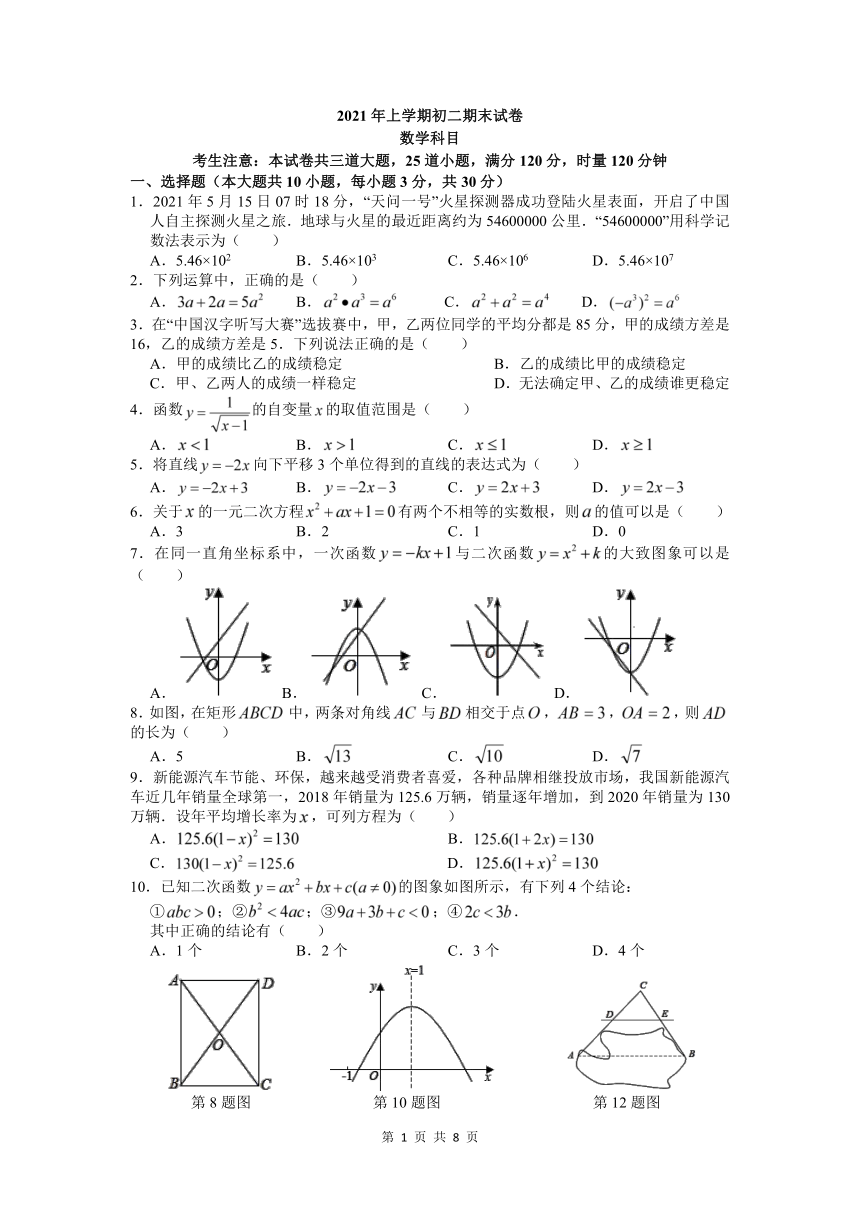 | |
| 格式 | docx | ||
| 文件大小 | 320.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 06:16:30 | ||
图片预览




文档简介
2021年上学期初二期末试卷
数学科目
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
一、选择题(本大题共10小题,每小题3分,共30分)
1.2021年5月15日07时18分,“天问一号”火星探测器成功登陆火星表面,开启了中国人自主探测火星之旅.地球与火星的最近距离约为54600000公里.“54600000”用科学记数法表示为( )
A.5.46×102
B.5.46×103
C.5.46×106
D.5.46×107
2.下列运算中,正确的是( )
A.
B.
C.
D.
3.在“中国汉字听写大赛”选拔赛中,甲,乙两位同学的平均分都是85分,甲的成绩方差是16,乙的成绩方差是5.下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
4.函数的自变量的取值范围是( )
A.
B.
C.
D.
5.将直线向下平移3个单位得到的直线的表达式为( )
A.
B.
C.
D.
6.关于的一元二次方程有两个不相等的实数根,则的值可以是( )
A.3
B.2
C.1
D.0
7.在同一直角坐标系中,一次函数与二次函数的大致图象可以是( )
A.
B.
C.
D.
8.如图,在矩形中,两条对角线与相交于点,,,则的长为( )
A.5
B.
C.
D.
9.新能源汽车节能、环保,越来越受消费者喜爱,各种品牌相继投放市场,我国新能源汽车近几年销量全球第一,2018年销量为125.6万辆,销量逐年增加,到2020年销量为130万辆.设年平均增长率为,可列方程为( )
A.
B.
C.
D.
10.已知二次函数的图象如图所示,有下列4个结论:
①;②;③;④.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
第8题图
第10题图
第12题图
二、填空题(本大题共6小题,每小题3分,满分18分)
11.分解因式:
.
如图,是池塘两端,设计一方法测量AB的距离,取点,连接、,再取它们的中点,测得米,则
米.
在平面直角坐标系xoy中,函数和的图象,如图所示,则不等式的解集为
.
若是方程的两个实数根,则
.
如图,在平行四边形中,,平分交于点,则的大小是
.
16.如图,是抛物线在第四象限的一点,过点分别向轴和轴作垂线,垂足分别为,则四边形周长的最大值为
.
第13题图
第15题图
第16题图
三、解答题(本大题共9小题,共72分)
17.(6分)计算:.
(6分)先化简,再求值:,其中.
19.(6分)已知,如图,一次函数的图象经过点和,与轴交于点.
(1)求一次函数的解析式;
(2)在轴上存在一点,且的面积为,求点的坐标.
20.(8分)某学校开展了防疫知识的宣传教育活动,为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分、得分均为不小于60的整数),测试成绩为60~70分记为基本合格,70~80分记为合格,80~90分记为良好,90~100分记为优秀,并制作如图统计图(部分信息未给出)
由图中给出的信息解答下列问题:
(1)本次测试抽取的学生人数有
名,并补全频数分布直方图.
(2)扇形统计图中“良好”所对应的扇形圆心角的度数为_________.
(3)这次测试成绩的中位数是_______等级(填“优秀、良好、合格或基本合格”).
(4)如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?
(8分)人教版初中数学教科书八年级下册第53页告诉我们直角三角形的一个性质:“直角三角形斜边上的中线等于斜边的一半”,我们一起来探究这条性质的证明过程:
如图,在中,,是斜边上的中线.
求证:.
证明:延长至点,使,连结.
请你根据以上提示,结合图形,写出完整的证明过程.
定理应用:如图,中,,点为边上一点,于点,连接,点为的中点,的延长线交于点,连接.
①线段与的数量关系是
;
②若是的平分线,且,则
.
(9分)兰兰打算买一束百合和康乃馨组合的鲜花,在“母亲节”祝福妈妈.已知买
1支康乃馨和2支百合共需花费23元,3支康乃馨的价格比2支百合的价格多5元.
(1)求买一支康乃馨和一支百合各需多少元?
(2)兰兰准备买康乃馨和百合共11支,且百合不少于2支.设买这束鲜花所需费用为元,康乃馨有x支,求与x之间的函数关系式,并设计一种使费用最少的买花方案,写出最少费用.
23.(9分)如图,,点分别是和上的点,连接交于点,此时.若于,解决下列问题:
(1)求证:;
(2)求证:四边形是菱形;
(3)求的长.
24.(10分)对于定点,其中,我们构造一个经过定点的“系函数”:若时,;若时,.
(1)已知点,则过点的“系函数”为
.
(2)已知点在第一象限内,且过点的“系函数”在时有整数解,求的值.
(3)已知点在直线的上方,且过点的“系函数”在时,,求的值.
25.(10分)如图,已知抛物线的对称轴为直线,且抛物线经过,两点,与轴交于点.
(1)求抛物线的解析式;
(2)若点从点出发,沿着射线运动,速度每秒个单位长度,过点作直线轴,交抛物线于点.设运动时间为t秒.
①在运动过程中,当t为何值时,使的值最大?并求出此时点的坐标。
②若点同时从点出发,向轴正方向运动,速度每秒个单位长度,问:是否存在t使点构成平行四边形?若存在,求出的值;若不存在,说明理由。
备用图
2021年上学期初二期末试卷
数学科目
参考答案
一、选择题(共10小题,满分30分,每小题3分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
B
B
A
A
D
D
A
二、填空题(共6小题,满分18分,每小题3分)
11.
12.20
13.
14.
15.144°
16.
三、解答题(共9小题,第17、18、19题每题6分,第20、21题每题8分,第22、23题每题9分,第24、25题每题10分,共72分)
17.原式=
18.原式,当时,原式=
19.(1)
(2)点的坐标为(-4,0)或(8,0)
20.】解:(1)抽取学生的总人数为:30÷15%=200(人);
故答案为:200;
如图即为补全的频数分布直方图;
(2)扇形统计图中“良好”所对应的扇形圆心角的度数是×360°=144°;
故答案为:144;
(3)这次测试成绩的中位数会落在良好等级;
故答案为:良好;
(4)×1500=300(人).
答:估计该校获得优秀的学生有300人.
21.(1)延长CD到E,使DE=CD,连接AE,BE,
则CD=CE,
∵CD是斜边AB上的中线,
∴AD=BD,
∴四边形ACBE是平行四边形,
∵∠ACB=90°,
∴平行四边形ACBE是矩形,
∴CE=AB,
∴CD=AB;
(2)①CM=EM
②
22.解:(1)设买一支康乃馨需a元,买一支百合需b元,
则根据题意得:,解得:
答:买一支康乃馨需7元,买一支百合需8元;
(2)根据题意得:w=7x+8(11-x)=-x+88,
∵百合不少于2支,
∴11-x≥2,
解得:x≤9,
∵-1<0,
∴w随x的增大而减小,
∴当x=9时,w最小,
即买9支康乃馨,买11-9=2支百合费用最少,w最小=-9+88=79(元),
答:w与x之间的函数关系式:w=-x+88,买9支康乃馨,买2支百合费用最少,最少费用为79元.
23.(1)∵
∴∠ADO=∠CBO
又∵∠AOD=∠COB,OA=OC
∴△AOD≌△COD(AAS)
∴OB=OD
(2)∵OB=OD,OA=OC
∴四边形ABCD为平形四边形
又∵
∴OB=OD=4,OA=OC=3
∴OB2+OA2=AB2
∴△AOB为直角三角形
∴AC⊥BD
∴四边形是菱形
(3)
24.(1)
(2)当时,,令时,方程无解,舍去
当时,,令时,解得
因为过点的“系函数”在时有整数解,即x为整数
又因为b>0
∴b=4,8,12
(3)略
25.(1)
(2)①易得直线BC的解析式为
设P(m,m+3),则点M为(m,-m2-2m+3)
∴
当时,最大
此时
所以此时
∴当时,使的值最大,此时点的坐标为(,)。②略
(
第
1
页
共
4
页
)
数学科目
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
一、选择题(本大题共10小题,每小题3分,共30分)
1.2021年5月15日07时18分,“天问一号”火星探测器成功登陆火星表面,开启了中国人自主探测火星之旅.地球与火星的最近距离约为54600000公里.“54600000”用科学记数法表示为( )
A.5.46×102
B.5.46×103
C.5.46×106
D.5.46×107
2.下列运算中,正确的是( )
A.
B.
C.
D.
3.在“中国汉字听写大赛”选拔赛中,甲,乙两位同学的平均分都是85分,甲的成绩方差是16,乙的成绩方差是5.下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
4.函数的自变量的取值范围是( )
A.
B.
C.
D.
5.将直线向下平移3个单位得到的直线的表达式为( )
A.
B.
C.
D.
6.关于的一元二次方程有两个不相等的实数根,则的值可以是( )
A.3
B.2
C.1
D.0
7.在同一直角坐标系中,一次函数与二次函数的大致图象可以是( )
A.
B.
C.
D.
8.如图,在矩形中,两条对角线与相交于点,,,则的长为( )
A.5
B.
C.
D.
9.新能源汽车节能、环保,越来越受消费者喜爱,各种品牌相继投放市场,我国新能源汽车近几年销量全球第一,2018年销量为125.6万辆,销量逐年增加,到2020年销量为130万辆.设年平均增长率为,可列方程为( )
A.
B.
C.
D.
10.已知二次函数的图象如图所示,有下列4个结论:
①;②;③;④.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
第8题图
第10题图
第12题图
二、填空题(本大题共6小题,每小题3分,满分18分)
11.分解因式:
.
如图,是池塘两端,设计一方法测量AB的距离,取点,连接、,再取它们的中点,测得米,则
米.
在平面直角坐标系xoy中,函数和的图象,如图所示,则不等式的解集为
.
若是方程的两个实数根,则
.
如图,在平行四边形中,,平分交于点,则的大小是
.
16.如图,是抛物线在第四象限的一点,过点分别向轴和轴作垂线,垂足分别为,则四边形周长的最大值为
.
第13题图
第15题图
第16题图
三、解答题(本大题共9小题,共72分)
17.(6分)计算:.
(6分)先化简,再求值:,其中.
19.(6分)已知,如图,一次函数的图象经过点和,与轴交于点.
(1)求一次函数的解析式;
(2)在轴上存在一点,且的面积为,求点的坐标.
20.(8分)某学校开展了防疫知识的宣传教育活动,为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分、得分均为不小于60的整数),测试成绩为60~70分记为基本合格,70~80分记为合格,80~90分记为良好,90~100分记为优秀,并制作如图统计图(部分信息未给出)
由图中给出的信息解答下列问题:
(1)本次测试抽取的学生人数有
名,并补全频数分布直方图.
(2)扇形统计图中“良好”所对应的扇形圆心角的度数为_________.
(3)这次测试成绩的中位数是_______等级(填“优秀、良好、合格或基本合格”).
(4)如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?
(8分)人教版初中数学教科书八年级下册第53页告诉我们直角三角形的一个性质:“直角三角形斜边上的中线等于斜边的一半”,我们一起来探究这条性质的证明过程:
如图,在中,,是斜边上的中线.
求证:.
证明:延长至点,使,连结.
请你根据以上提示,结合图形,写出完整的证明过程.
定理应用:如图,中,,点为边上一点,于点,连接,点为的中点,的延长线交于点,连接.
①线段与的数量关系是
;
②若是的平分线,且,则
.
(9分)兰兰打算买一束百合和康乃馨组合的鲜花,在“母亲节”祝福妈妈.已知买
1支康乃馨和2支百合共需花费23元,3支康乃馨的价格比2支百合的价格多5元.
(1)求买一支康乃馨和一支百合各需多少元?
(2)兰兰准备买康乃馨和百合共11支,且百合不少于2支.设买这束鲜花所需费用为元,康乃馨有x支,求与x之间的函数关系式,并设计一种使费用最少的买花方案,写出最少费用.
23.(9分)如图,,点分别是和上的点,连接交于点,此时.若于,解决下列问题:
(1)求证:;
(2)求证:四边形是菱形;
(3)求的长.
24.(10分)对于定点,其中,我们构造一个经过定点的“系函数”:若时,;若时,.
(1)已知点,则过点的“系函数”为
.
(2)已知点在第一象限内,且过点的“系函数”在时有整数解,求的值.
(3)已知点在直线的上方,且过点的“系函数”在时,,求的值.
25.(10分)如图,已知抛物线的对称轴为直线,且抛物线经过,两点,与轴交于点.
(1)求抛物线的解析式;
(2)若点从点出发,沿着射线运动,速度每秒个单位长度,过点作直线轴,交抛物线于点.设运动时间为t秒.
①在运动过程中,当t为何值时,使的值最大?并求出此时点的坐标。
②若点同时从点出发,向轴正方向运动,速度每秒个单位长度,问:是否存在t使点构成平行四边形?若存在,求出的值;若不存在,说明理由。
备用图
2021年上学期初二期末试卷
数学科目
参考答案
一、选择题(共10小题,满分30分,每小题3分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
B
B
A
A
D
D
A
二、填空题(共6小题,满分18分,每小题3分)
11.
12.20
13.
14.
15.144°
16.
三、解答题(共9小题,第17、18、19题每题6分,第20、21题每题8分,第22、23题每题9分,第24、25题每题10分,共72分)
17.原式=
18.原式,当时,原式=
19.(1)
(2)点的坐标为(-4,0)或(8,0)
20.】解:(1)抽取学生的总人数为:30÷15%=200(人);
故答案为:200;
如图即为补全的频数分布直方图;
(2)扇形统计图中“良好”所对应的扇形圆心角的度数是×360°=144°;
故答案为:144;
(3)这次测试成绩的中位数会落在良好等级;
故答案为:良好;
(4)×1500=300(人).
答:估计该校获得优秀的学生有300人.
21.(1)延长CD到E,使DE=CD,连接AE,BE,
则CD=CE,
∵CD是斜边AB上的中线,
∴AD=BD,
∴四边形ACBE是平行四边形,
∵∠ACB=90°,
∴平行四边形ACBE是矩形,
∴CE=AB,
∴CD=AB;
(2)①CM=EM
②
22.解:(1)设买一支康乃馨需a元,买一支百合需b元,
则根据题意得:,解得:
答:买一支康乃馨需7元,买一支百合需8元;
(2)根据题意得:w=7x+8(11-x)=-x+88,
∵百合不少于2支,
∴11-x≥2,
解得:x≤9,
∵-1<0,
∴w随x的增大而减小,
∴当x=9时,w最小,
即买9支康乃馨,买11-9=2支百合费用最少,w最小=-9+88=79(元),
答:w与x之间的函数关系式:w=-x+88,买9支康乃馨,买2支百合费用最少,最少费用为79元.
23.(1)∵
∴∠ADO=∠CBO
又∵∠AOD=∠COB,OA=OC
∴△AOD≌△COD(AAS)
∴OB=OD
(2)∵OB=OD,OA=OC
∴四边形ABCD为平形四边形
又∵
∴OB=OD=4,OA=OC=3
∴OB2+OA2=AB2
∴△AOB为直角三角形
∴AC⊥BD
∴四边形是菱形
(3)
24.(1)
(2)当时,,令时,方程无解,舍去
当时,,令时,解得
因为过点的“系函数”在时有整数解,即x为整数
又因为b>0
∴b=4,8,12
(3)略
25.(1)
(2)①易得直线BC的解析式为
设P(m,m+3),则点M为(m,-m2-2m+3)
∴
当时,最大
此时
所以此时
∴当时,使的值最大,此时点的坐标为(,)。②略
(
第
1
页
共
4
页
)
同课章节目录
