scg1zbwl101009 由物理过程的分析求极值
文档属性
| 名称 | scg1zbwl101009 由物理过程的分析求极值 |

|
|
| 格式 | zip | ||
| 文件大小 | 113.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-05-04 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
例2.火车以速度v1 匀速行驶,司机发现前方同轨道上相距s处有另一列火车同方向以速度v2(对地),且v1>v2做匀速运动。司机立即以加速度a紧急刹车,要使两车不相撞,a应满足什么条件?
两辆火车不相撞的临界条件是什么?
解法一:由物理过程的分析求极值
后车刹车后做匀减速运动,若后车加速度大小为某值时,恰能使两车在速度相等时后车追上前车,这正是两车恰不相撞的临界条件,此时对应的加速度即为两车不相撞的最小加速度a0。
两车恰不相撞时应满足以下两方程:
速度关系 v1 - a0t = v2
位移关系 v1t - a0 t2/2 = v2t +s
联立求解这两个方程可得a0 = ( v2 -v1)2/2s
所以当 a≥ ( v2 -v1)2/2s时,两车就不会相撞。
解法二:利用数学方法求极值
要使两车不相撞,
其位移关系应为v1t - a t2/2 ≤ v2t +s
即 a t2/2+ ( v2 - v1) t +s≥0,
该不等式任意时刻都成立,
则其系数必须满足
△ = b2 - 4ac≤ 0
即△ = ( v2 - v1)2 - 2as ≤0
由此解出a≥ ( v2 -v1)2/2s
解法三:巧选参考系
选前车为参考系,刹车后后车相对于前车作初速度为v0 = v1 – v2,加速度为a的匀减速运动,当后车相对前车的速度减为零时,若相对位移s'≤s,则不会相撞。故由
s' = ≤ s 得a≥ ( v2 -v1)2/2s
小结:关键是利用时间关系、速度关系、位移关系列出方程求解。 笫一、追及问题中两者的速度相等时,两者距离是极大值或极小值; 笫二、相向运动的物体,当各自发生的位移的绝对值之和等于开始时两物体间的距离时即相遇。
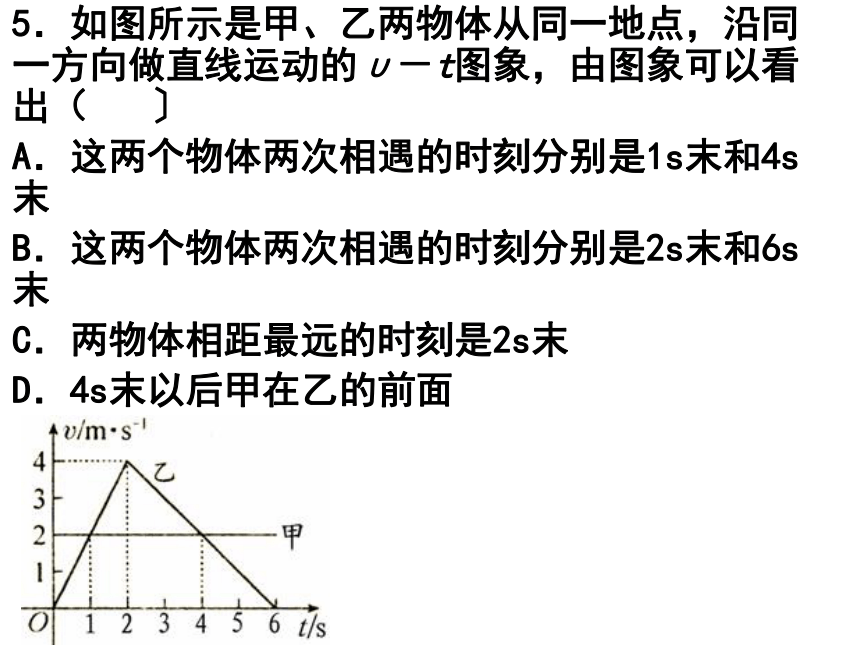
5.如图所示是甲、乙两物体从同一地点,沿同一方向做直线运动的υ-t图象,由图象可以看出( 〕
A.这两个物体两次相遇的时刻分别是1s末和4s末
B.这两个物体两次相遇的时刻分别是2s末和6s末
C.两物体相距最远的时刻是2s末
D.4s末以后甲在乙的前面
7.如图所示,a、b分别是甲、乙两辆车从同一地点沿同一直线同时运动的图线,由图线可以判断( )
A.2秒后甲、乙两车的加速度大小相等
B.在0~8s内两车最远相距148 m
C.两车只有t0时刻速率相等
D.两车在t=8s时相遇
8.两辆游戏赛车a、b在两条平行的直车道上行驶,t=0时两车都在同一计时线处,此时比赛开始.它们在四次比赛中的υ-t图如图所示,哪些图对应的比赛中,有一辆赛车追上了另一辆( )
11.A、B两棒均长1m,A棒悬挂于天花板上,B棒与A棒在一条竖直线上,直立在地面,A棒的下端与B棒的上端之间相距20m,某时刻烧断悬挂A棒的绳子,同时将B棒以v0=20m/s的初速度竖直上抛,若空气阻力可忽略不计,且g=10m/s2,试求:
(1)A、B两棒出发后何时相遇?
(2)A、B两棒相遇后,交错而过需用多少时间?
周末练习三
1.C 2.AB 3.ACD 4.ACD 5.B 6.D 7.B 8.AC 9. 10. -2 11.(1) 1s (2) 0.1s
2.25m/s2 13.53m 18m 55m
14. (1)1.75 m/s (2)2颗 15. 12.8m/s 50s
16. (1)3.2m (2)0.2s 17. 1.7s
周末练习四
1.B 2.B 3.D 4.AB 5.AC 6.BCDEFG 7.D 8.B 9.C 10.BD 11.C 12.C 13. 14.B 16. 3 3 1.05
17.作出假设、 搜索证据.匀速 1.937.加速度逐渐减小的加速 匀速 图线1反映速度不随时间变化,图线5反映速度随时间继续增大(或图线1反映纸杯做匀速运动,图线5反映纸杯依然在做加速度减小的加速运动.
18. 80m/s 800m 4m/s 7.1m/s
19. 900m
20. 20 m 22. 3a 2v
作业:
1.三维设计第八节,第九节和章末小结与测评的尝试应用,例题,跟踪演练。(有答案的例题也要自己做)
2.自己总结本章知识点网络,写在作业本上。(不会的同学参考三维P26)
例2.火车以速度v1 匀速行驶,司机发现前方同轨道上相距s处有另一列火车同方向以速度v2(对地),且v1>v2做匀速运动。司机立即以加速度a紧急刹车,要使两车不相撞,a应满足什么条件?
两辆火车不相撞的临界条件是什么?
解法一:由物理过程的分析求极值
后车刹车后做匀减速运动,若后车加速度大小为某值时,恰能使两车在速度相等时后车追上前车,这正是两车恰不相撞的临界条件,此时对应的加速度即为两车不相撞的最小加速度a0。
两车恰不相撞时应满足以下两方程:
速度关系 v1 - a0t = v2
位移关系 v1t - a0 t2/2 = v2t +s
联立求解这两个方程可得a0 = ( v2 -v1)2/2s
所以当 a≥ ( v2 -v1)2/2s时,两车就不会相撞。
解法二:利用数学方法求极值
要使两车不相撞,
其位移关系应为v1t - a t2/2 ≤ v2t +s
即 a t2/2+ ( v2 - v1) t +s≥0,
该不等式任意时刻都成立,
则其系数必须满足
△ = b2 - 4ac≤ 0
即△ = ( v2 - v1)2 - 2as ≤0
由此解出a≥ ( v2 -v1)2/2s
解法三:巧选参考系
选前车为参考系,刹车后后车相对于前车作初速度为v0 = v1 – v2,加速度为a的匀减速运动,当后车相对前车的速度减为零时,若相对位移s'≤s,则不会相撞。故由
s' = ≤ s 得a≥ ( v2 -v1)2/2s
小结:关键是利用时间关系、速度关系、位移关系列出方程求解。 笫一、追及问题中两者的速度相等时,两者距离是极大值或极小值; 笫二、相向运动的物体,当各自发生的位移的绝对值之和等于开始时两物体间的距离时即相遇。
5.如图所示是甲、乙两物体从同一地点,沿同一方向做直线运动的υ-t图象,由图象可以看出( 〕
A.这两个物体两次相遇的时刻分别是1s末和4s末
B.这两个物体两次相遇的时刻分别是2s末和6s末
C.两物体相距最远的时刻是2s末
D.4s末以后甲在乙的前面
7.如图所示,a、b分别是甲、乙两辆车从同一地点沿同一直线同时运动的图线,由图线可以判断( )
A.2秒后甲、乙两车的加速度大小相等
B.在0~8s内两车最远相距148 m
C.两车只有t0时刻速率相等
D.两车在t=8s时相遇
8.两辆游戏赛车a、b在两条平行的直车道上行驶,t=0时两车都在同一计时线处,此时比赛开始.它们在四次比赛中的υ-t图如图所示,哪些图对应的比赛中,有一辆赛车追上了另一辆( )
11.A、B两棒均长1m,A棒悬挂于天花板上,B棒与A棒在一条竖直线上,直立在地面,A棒的下端与B棒的上端之间相距20m,某时刻烧断悬挂A棒的绳子,同时将B棒以v0=20m/s的初速度竖直上抛,若空气阻力可忽略不计,且g=10m/s2,试求:
(1)A、B两棒出发后何时相遇?
(2)A、B两棒相遇后,交错而过需用多少时间?
周末练习三
1.C 2.AB 3.ACD 4.ACD 5.B 6.D 7.B 8.AC 9. 10. -2 11.(1) 1s (2) 0.1s
2.25m/s2 13.53m 18m 55m
14. (1)1.75 m/s (2)2颗 15. 12.8m/s 50s
16. (1)3.2m (2)0.2s 17. 1.7s
周末练习四
1.B 2.B 3.D 4.AB 5.AC 6.BCDEFG 7.D 8.B 9.C 10.BD 11.C 12.C 13. 14.B 16. 3 3 1.05
17.作出假设、 搜索证据.匀速 1.937.加速度逐渐减小的加速 匀速 图线1反映速度不随时间变化,图线5反映速度随时间继续增大(或图线1反映纸杯做匀速运动,图线5反映纸杯依然在做加速度减小的加速运动.
18. 80m/s 800m 4m/s 7.1m/s
19. 900m
20. 20 m 22. 3a 2v
作业:
1.三维设计第八节,第九节和章末小结与测评的尝试应用,例题,跟踪演练。(有答案的例题也要自己做)
2.自己总结本章知识点网络,写在作业本上。(不会的同学参考三维P26)
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
