平行线的性质
图片预览






文档简介
(共23张PPT)
5.3.1平行线的性质
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( )
E
A
C
D
B
1
2
3
4
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
平行线的性质
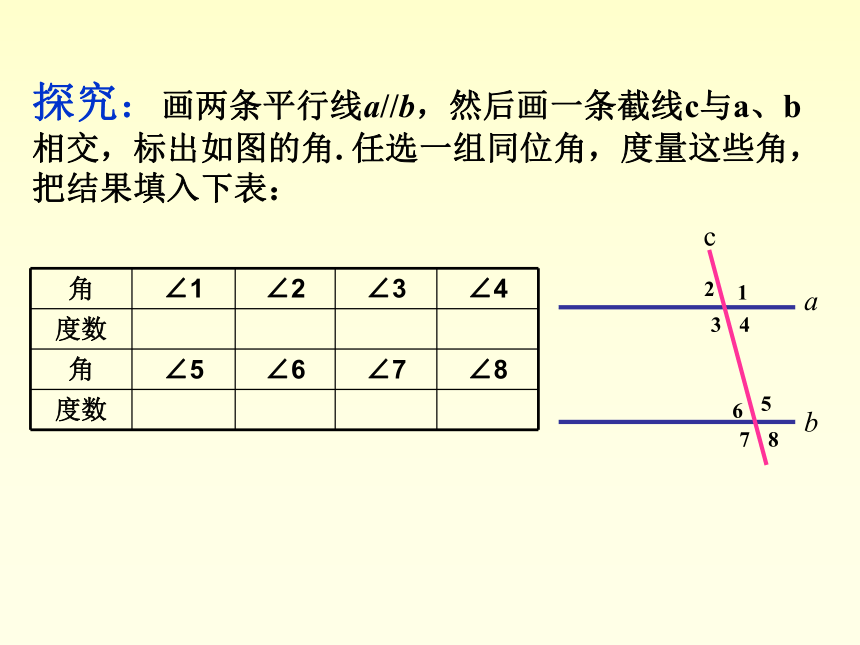
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
1
3
2
4
8
5
7
6
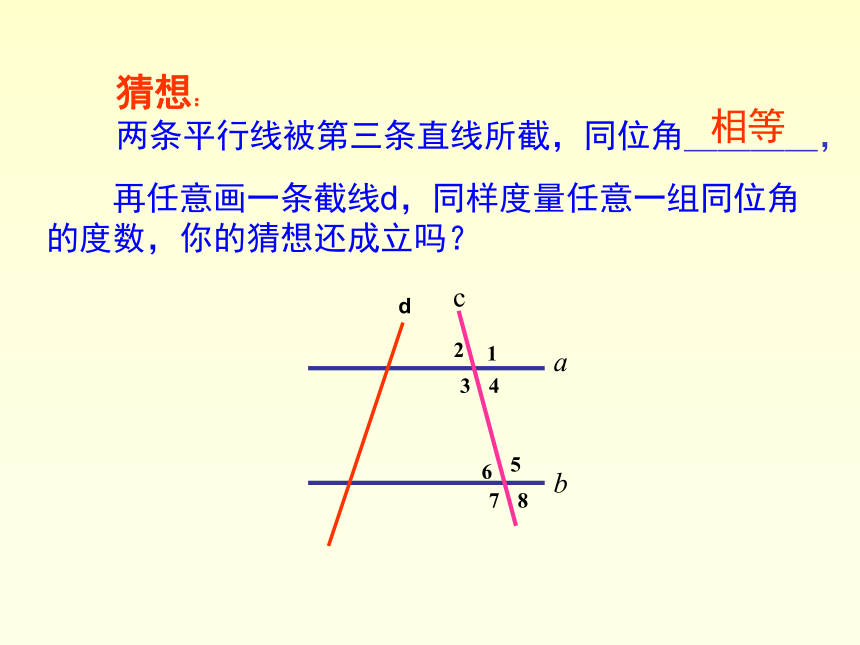
猜想:
两条平行线被第三条直线所截,同位角____,
再任意画一条截线d,同样度量任意一组同位角的度数,你的猜想还成立吗?
相等
a
b
c
1
3
2
4
8
5
7
6
d
性质1:两条平行线被第三条直线所截,同位角相等.
平行线的性质:
简单说成:两直线平行,同位角相等.
a
b
c
1
2
3
4
∵a∥b ∴∠1=∠2
如图,a∥b,如果∠1=700
那么 ∠2= , ∠3 = .
700
700
如图,若a∥b,则∠2与∠3 相等吗?
平行线的性质:
a
b
c
1
2
3
4
如图,若a∥b,则∠2与∠3 相等吗?请说明理由.
解: ∠2 = ∠ 3. 理由是:
∵a∥b (已知)
∴ ∠1= ∠2( )
∵ ∠1=∠3 ( )
∴ ∠2= ∠3. ( )
两直线平行, 同位角相等
对顶角相等
等量代换
平行线的性质:
a
b
c
1
2
3
4
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
∵a∥b ∴ ∠2=∠3
如图,若a∥b,则∠2与∠4 互补吗?为什么?
解:∠2+∠4=1800. 理由是:
∵a∥b (已知)
∴ ∠1= ∠2.(两直线平行,同位角相等)
∵ ∠1+ ∠4=1800 (邻补角定义)
∴ ∠2+∠4=1800 . (等量代换)
平行线的性质:
a
b
c
1
2
3
4
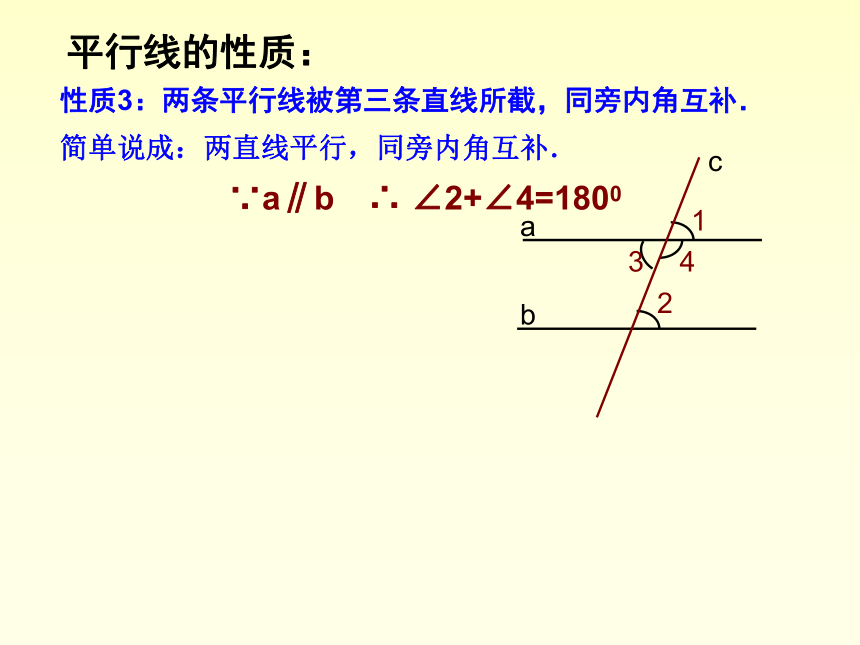
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
∵a∥b ∴ ∠2+∠4=1800
图形
已知
结果
理由
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
∠1 =∠2
∠2 =∠3
∠2与∠4
互补
1.如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是1420,第二次 拐的角∠C= ,理由是: .
B
C
两直线平行,内错角相等
142o
一、填空
2.如图,直线a∥b, ∠ 1=54 ,
那么∠2= ,
∠3= ,
∠4= .
1
2
3
4
54
54
126
3.如图,直线DE经过点A,DE∥BC , 那么∠B = 44°,
∠C =57 °.则∠1= ,∠2= ,∠3= ,
∠3+ ∠B +∠C= .
44°
79°
180°
57°
A
B
C
D
E
3
1
2
44°
57°
180°
通过这道题,你能猜想三角形的三个内角和是多少度吗?
2. 如图,直线 a∥b,则∠1=∠2 ( )
×
×
1
2
a
b
二、判断
1.如果有两条直线被第三条直线所截,那么
必定有同位角相等( )
1.如图,由AB∥CD ,若∠A= 120°则
∠C=( )
(A)40° (B) 50°
(C) 60° (D) 70°
C
B
A
D
C
三、选择
2.如图,由AB∥CD ∥EF , 那么
∠BAC+ ∠ACE+ ∠CEF=( )
(A)180° (B) 270°
(C) 360° (D) 540°
C
B
A
D
C
E
F
C
D
1.如图,若AB∥DE,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
P
F
C
E
B
A
D
解: ∠A =∠D. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D=____ ( )
∴∠A=∠D ( )
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
四、解答题
3. 如图所示是一块梯形铁片的残余部分,量得∠A=100 , ∠B=115°,梯形另外两个角各是多少度?
解:∵AB//CD(已知)
∴ A + D=180° (两直线平行,同旁内角互补)
B + C=180° (两直线平行,同旁内角互补)
∴ D=180 ° - A= 180 °-100 ° =80 °
C=180 ° - B= 180 °-115° =65 °
答:梯形的另外两个角分别为80 °, 65 °.
4.如图,D是AB上一点,E是AC上一点,
∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE∥BC 理由是:
∵ ∠ADE=60°,∠B=60°
∴ ∠ADE= ∠B
∴ DE∥BC ( )
同位角相等,两直线平行
(2) ∠C =40°理由是:
∵DE∥BC
∴∠C = ∠AED( )
∵∠AED=40°
∴∠C =40°.
两直线平行,同位角相等
E
D
C
B
A
平行线的“判定”与“性质”有什么不同
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
(1)请你谈谈本节课的收获和感受。
小结与回顾:
(2)说说平行线的“判定”与“性质”有什么不同
D
C
E
F
A
A
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
5.3.1平行线的性质
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,
那么__∥__( )
E
A
C
D
B
1
2
3
4
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
平行线的性质
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
1
3
2
4
8
5
7
6
猜想:
两条平行线被第三条直线所截,同位角____,
再任意画一条截线d,同样度量任意一组同位角的度数,你的猜想还成立吗?
相等
a
b
c
1
3
2
4
8
5
7
6
d
性质1:两条平行线被第三条直线所截,同位角相等.
平行线的性质:
简单说成:两直线平行,同位角相等.
a
b
c
1
2
3
4
∵a∥b ∴∠1=∠2
如图,a∥b,如果∠1=700
那么 ∠2= , ∠3 = .
700
700
如图,若a∥b,则∠2与∠3 相等吗?
平行线的性质:
a
b
c
1
2
3
4
如图,若a∥b,则∠2与∠3 相等吗?请说明理由.
解: ∠2 = ∠ 3. 理由是:
∵a∥b (已知)
∴ ∠1= ∠2( )
∵ ∠1=∠3 ( )
∴ ∠2= ∠3. ( )
两直线平行, 同位角相等
对顶角相等
等量代换
平行线的性质:
a
b
c
1
2
3
4
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
∵a∥b ∴ ∠2=∠3
如图,若a∥b,则∠2与∠4 互补吗?为什么?
解:∠2+∠4=1800. 理由是:
∵a∥b (已知)
∴ ∠1= ∠2.(两直线平行,同位角相等)
∵ ∠1+ ∠4=1800 (邻补角定义)
∴ ∠2+∠4=1800 . (等量代换)
平行线的性质:
a
b
c
1
2
3
4
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
∵a∥b ∴ ∠2+∠4=1800
图形
已知
结果
理由
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
∠1 =∠2
∠2 =∠3
∠2与∠4
互补
1.如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是1420,第二次 拐的角∠C= ,理由是: .
B
C
两直线平行,内错角相等
142o
一、填空
2.如图,直线a∥b, ∠ 1=54 ,
那么∠2= ,
∠3= ,
∠4= .
1
2
3
4
54
54
126
3.如图,直线DE经过点A,DE∥BC , 那么∠B = 44°,
∠C =57 °.则∠1= ,∠2= ,∠3= ,
∠3+ ∠B +∠C= .
44°
79°
180°
57°
A
B
C
D
E
3
1
2
44°
57°
180°
通过这道题,你能猜想三角形的三个内角和是多少度吗?
2. 如图,直线 a∥b,则∠1=∠2 ( )
×
×
1
2
a
b
二、判断
1.如果有两条直线被第三条直线所截,那么
必定有同位角相等( )
1.如图,由AB∥CD ,若∠A= 120°则
∠C=( )
(A)40° (B) 50°
(C) 60° (D) 70°
C
B
A
D
C
三、选择
2.如图,由AB∥CD ∥EF , 那么
∠BAC+ ∠ACE+ ∠CEF=( )
(A)180° (B) 270°
(C) 360° (D) 540°
C
B
A
D
C
E
F
C
D
1.如图,若AB∥DE,AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
P
F
C
E
B
A
D
解: ∠A =∠D. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D=____ ( )
∴∠A=∠D ( )
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
四、解答题
3. 如图所示是一块梯形铁片的残余部分,量得∠A=100 , ∠B=115°,梯形另外两个角各是多少度?
解:∵AB//CD(已知)
∴ A + D=180° (两直线平行,同旁内角互补)
B + C=180° (两直线平行,同旁内角互补)
∴ D=180 ° - A= 180 °-100 ° =80 °
C=180 ° - B= 180 °-115° =65 °
答:梯形的另外两个角分别为80 °, 65 °.
4.如图,D是AB上一点,E是AC上一点,
∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
解:(1)DE∥BC 理由是:
∵ ∠ADE=60°,∠B=60°
∴ ∠ADE= ∠B
∴ DE∥BC ( )
同位角相等,两直线平行
(2) ∠C =40°理由是:
∵DE∥BC
∴∠C = ∠AED( )
∵∠AED=40°
∴∠C =40°.
两直线平行,同位角相等
E
D
C
B
A
平行线的“判定”与“性质”有什么不同
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
(1)请你谈谈本节课的收获和感受。
小结与回顾:
(2)说说平行线的“判定”与“性质”有什么不同
D
C
E
F
A
A
G
G
1
2
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
