函数综合
图片预览


文档简介
函数综合
一)一次函数
2011江苏盐城):如图,已知一次函数y=--x+7与正比例函数y=x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;A(3.4) B(7 .0)
(2)过点A作AC⊥y轴于点C,过点B作直线L∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动;同时直线L从点B出发,以相同速度向左平移,在平移过程中,直线L交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线L都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?2 3和6舍去
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.1 5
2009年山西》如图,已知直线L1:y=x+与直线L2:y=-2x+16相交于点C,L1、L2分别交x轴于A、B两点.矩形DEFG的顶点D、E分别在直线L1、L2上,顶点F、G都在x轴上,且点G与点B重合.
(1)求△ABC的面积;(36)
(2)求矩形DEFG的边DE与EF的长;4 8
(3)若矩形DEFG沿x轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤12)秒,矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围.
1》s=--t2+t+(0t <3)
s=--t+(3t<8)
s=t2-8t+48(8t12)
二)反比例函数
2010河南》 如图,直线y=k1x+b与反比例y=函数的图象交于A(1,6),B(a,3)两点.
(1)求k1、k2的值.
(2)直接写出k1x+b-->0时x的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数y=的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
2010甘肃兰州》如图,P1是反比例函数y=(k>0)在第一象限图象上的一点,点A1的坐标为(2,0).
(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?△P1OA1的面积将逐渐
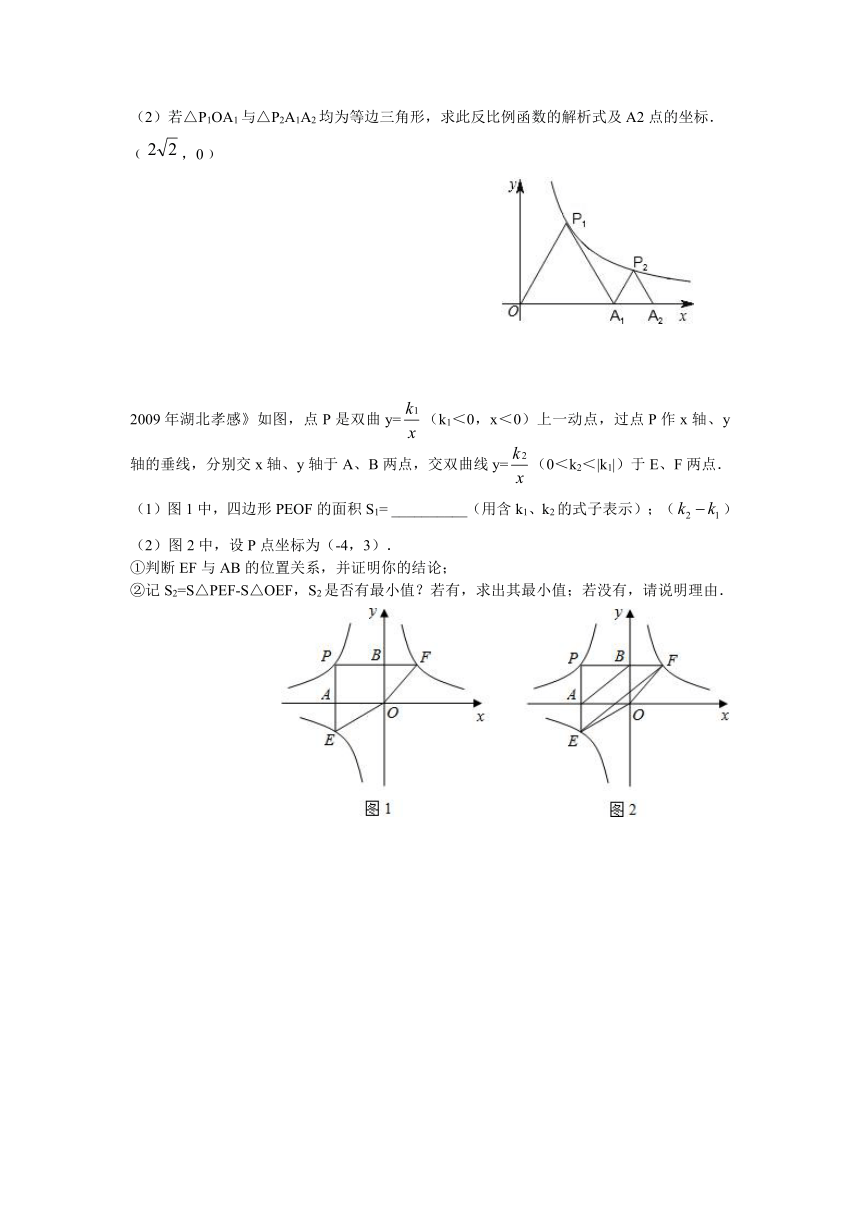
(2)若△P1OA1与△P2A1A2均为等边三角形,求此反比例函数的解析式及A2点的坐标.
﹙,0﹚
2009年湖北孝感》如图,点P是双曲y=(k1<0,x<0)上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=(0<k2<|k1|)于E、F两点.
(1)图1中,四边形PEOF的面积S1= __________(用含k1、k2的式子表示);()
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记S2=S△PEF-S△OEF,S2是否有最小值?若有,求出其最小值;若没有,请说明理由.
S2=当时,S2的值随k2的增大而增大,而0<k2<12.
0<S2<24,s2没有最小值.
三)一次函数与反比例函数的综合问题
2010)已知双曲线与直线相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
2011年四川宜宾)如图,一次函数的图象与反比例函数y1= – ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
求一次函数的解析式;
设函数y2= (x>0)的图象与y1= – (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
四)一次函数与二次函数的综合
2010湖北荆门)已知:如图一次函数y=x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=x2+bx+c的图象与一次函数y=x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
2009年江西)如图,抛物线与轴相交于、两点(点在点的左侧),与轴相交于点,顶点为.
(1)直接写出、、三点的坐标和抛物线的对称轴;
(2)连接,与抛物线的对称轴交于点,点为线段上的一个动点,过点作交抛物线于点,设点的横坐标为;
①用含的代数式表示线段的长,并求出当为何值时,四边形为平行四边形?
②设的面积为,求与的函数关系式.
(3)如图,分别作AA1⊥x轴,MM1⊥x轴,垂足分别为A1、M1.
设A点的横坐标为a,则B点的横坐标为-a.于是
.
同理,……………………………13分
∴.……………………14分
(2)∵y2 = (x>0)的图象与y1= – (x<0)的图象y轴对称,
∴y2 = (x>0) (4分)
∵B点是直线y= –x+2与y轴的交点,∴B (0,2) (5分)
设P(n, ),n>2 S四边形BCQP –S△BOC =2∴( 2+ )n– 22 = 2,n = , 分)
∴P(,) (7分)
(3)设符合条件的点P存在,令P(a,0):
当P为直角顶点时,如图:过C作CF⊥x轴于F.
∵Rt△BOP∽Rt△PFC,∴.即.
整理得a2-4a+3=0.解得a=1或a=3
∴所求的点P的坐标为(1,0)或(3,0)
综上所述:满足条件的点P共有二个………………………………………………………12分
解:(1)A(-1,0),B(3,0),C(0,3). 2分
抛物线的对称轴是:x=1. 3分
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
解得:k= -1,b=3.
所以直线BC的函数关系式为:.
当x=1时,y= -1+3=2,∴E(1,2).
当时,,
∴P(m,m+3). 4分
在中,当时,
∴
当时,∴ 5分
∴线段DE=4-2=2,线段 6分
∵
∴当时,四边形为平行四边形.
由解得:(不合题意,舍去).
因此,当时,四边形为平行四边形. 7分
②设直线与轴交于点,由可得:
∵ 8分
即.
9分
说明:1.第(1)问,写对1个或2个点的坐标均给1分,写对3个点的坐标得2分;
O
B
x
y
y=--x+7
y=x
A
(第28题)
y
O
·
A
D
x
B
C
E
N
M
·
(21题图)
第24题图
x
y
D
C
A
O
B
(第24题)
(第28题)
y
O
·
A
x
B
M
·
Q
A1
P
M1
第24题图
x
y
D
C
A
O
B
E
P
F
M
(第24题)
一)一次函数
2011江苏盐城):如图,已知一次函数y=--x+7与正比例函数y=x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;A(3.4) B(7 .0)
(2)过点A作AC⊥y轴于点C,过点B作直线L∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动;同时直线L从点B出发,以相同速度向左平移,在平移过程中,直线L交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线L都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?2 3和6舍去
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.1 5
2009年山西》如图,已知直线L1:y=x+与直线L2:y=-2x+16相交于点C,L1、L2分别交x轴于A、B两点.矩形DEFG的顶点D、E分别在直线L1、L2上,顶点F、G都在x轴上,且点G与点B重合.
(1)求△ABC的面积;(36)
(2)求矩形DEFG的边DE与EF的长;4 8
(3)若矩形DEFG沿x轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤12)秒,矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围.
1》s=--t2+t+(0t <3)
s=--t+(3t<8)
s=t2-8t+48(8t12)
二)反比例函数
2010河南》 如图,直线y=k1x+b与反比例y=函数的图象交于A(1,6),B(a,3)两点.
(1)求k1、k2的值.
(2)直接写出k1x+b-->0时x的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数y=的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
2010甘肃兰州》如图,P1是反比例函数y=(k>0)在第一象限图象上的一点,点A1的坐标为(2,0).
(1)当点P1的横坐标逐渐增大时,△P1OA1的面积将如何变化?△P1OA1的面积将逐渐
(2)若△P1OA1与△P2A1A2均为等边三角形,求此反比例函数的解析式及A2点的坐标.
﹙,0﹚
2009年湖北孝感》如图,点P是双曲y=(k1<0,x<0)上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=(0<k2<|k1|)于E、F两点.
(1)图1中,四边形PEOF的面积S1= __________(用含k1、k2的式子表示);()
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记S2=S△PEF-S△OEF,S2是否有最小值?若有,求出其最小值;若没有,请说明理由.
S2=当时,S2的值随k2的增大而增大,而0<k2<12.
0<S2<24,s2没有最小值.
三)一次函数与反比例函数的综合问题
2010)已知双曲线与直线相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
2011年四川宜宾)如图,一次函数的图象与反比例函数y1= – ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
求一次函数的解析式;
设函数y2= (x>0)的图象与y1= – (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
四)一次函数与二次函数的综合
2010湖北荆门)已知:如图一次函数y=x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=x2+bx+c的图象与一次函数y=x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
2009年江西)如图,抛物线与轴相交于、两点(点在点的左侧),与轴相交于点,顶点为.
(1)直接写出、、三点的坐标和抛物线的对称轴;
(2)连接,与抛物线的对称轴交于点,点为线段上的一个动点,过点作交抛物线于点,设点的横坐标为;
①用含的代数式表示线段的长,并求出当为何值时,四边形为平行四边形?
②设的面积为,求与的函数关系式.
(3)如图,分别作AA1⊥x轴,MM1⊥x轴,垂足分别为A1、M1.
设A点的横坐标为a,则B点的横坐标为-a.于是
.
同理,……………………………13分
∴.……………………14分
(2)∵y2 = (x>0)的图象与y1= – (x<0)的图象y轴对称,
∴y2 = (x>0) (4分)
∵B点是直线y= –x+2与y轴的交点,∴B (0,2) (5分)
设P(n, ),n>2 S四边形BCQP –S△BOC =2∴( 2+ )n– 22 = 2,n = , 分)
∴P(,) (7分)
(3)设符合条件的点P存在,令P(a,0):
当P为直角顶点时,如图:过C作CF⊥x轴于F.
∵Rt△BOP∽Rt△PFC,∴.即.
整理得a2-4a+3=0.解得a=1或a=3
∴所求的点P的坐标为(1,0)或(3,0)
综上所述:满足条件的点P共有二个………………………………………………………12分
解:(1)A(-1,0),B(3,0),C(0,3). 2分
抛物线的对称轴是:x=1. 3分
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
解得:k= -1,b=3.
所以直线BC的函数关系式为:.
当x=1时,y= -1+3=2,∴E(1,2).
当时,,
∴P(m,m+3). 4分
在中,当时,
∴
当时,∴ 5分
∴线段DE=4-2=2,线段 6分
∵
∴当时,四边形为平行四边形.
由解得:(不合题意,舍去).
因此,当时,四边形为平行四边形. 7分
②设直线与轴交于点,由可得:
∵ 8分
即.
9分
说明:1.第(1)问,写对1个或2个点的坐标均给1分,写对3个点的坐标得2分;
O
B
x
y
y=--x+7
y=x
A
(第28题)
y
O
·
A
D
x
B
C
E
N
M
·
(21题图)
第24题图
x
y
D
C
A
O
B
(第24题)
(第28题)
y
O
·
A
x
B
M
·
Q
A1
P
M1
第24题图
x
y
D
C
A
O
B
E
P
F
M
(第24题)
同课章节目录
