安徽省蚌埠铁路中学2012届九年级下学期期中考试数学试题(无答案)
文档属性
| 名称 | 安徽省蚌埠铁路中学2012届九年级下学期期中考试数学试题(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 124.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-04 00:00:00 | ||
图片预览


文档简介
蚌埠铁路中学2011----2012学年第二学期初三期中试卷
数 学
时间:120分钟 满分: 150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
得分 评卷人 一、选择题:(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只一项是符合题目要求的,请将正确选项的序号填写在题后的括号内)
1.9的算术平方根是( )。
A.3 B.-3 C.81 D. -81
2.下列运算正确的是( )。
A. 22.32 =64 B.
C. D.
3.不等式组的解集为( )
A.x>3 B.x≤4 C. 34.2011年8月22日,经国务院批准,安徽省对行政区进行了调整,合肥市的区域面积从7029平方千米扩大到11400平方千米,将数据11400用科学记数法表示为( )。
A.0.114×105 B.11.4×103 C.1.14×104 D.114×102
5.化简: 的结果是( )。
A.2 B. C. D.
6.若一个菱形的边长为2,则这个菱形两条对角线的平方和为( )。
A.16 B. 8 C.4 D. 1
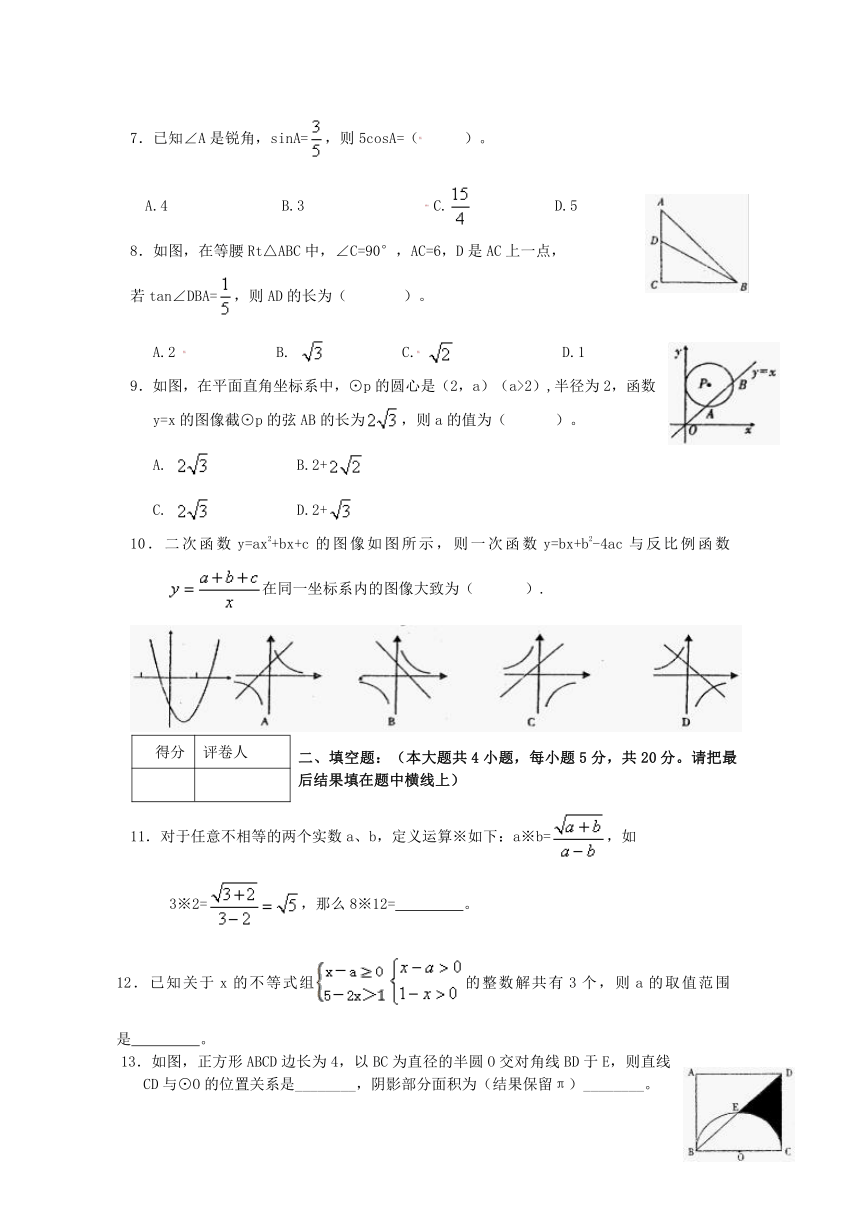
7.已知∠A是锐角,sinA=,则5cosA=( )。
A.4 B.3 C. D.5
8.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,
若tan∠DBA=,则AD的长为( )。
A.2 B. C. D.1
9.如图,在平面直角坐标系中,⊙p的圆心是(2,a)(a>2),半径为2,函数y=x的图像截⊙p的弦AB的长为,则a的值为( )。
A. B.2+
C. D.2+
10.二次函数y=ax2+bx+c的图像如图所示,则一次函数y=bx+b2-4ac与反比例函数在同一坐标系内的图像大致为( ).
得分 评卷人 二、填空题:(本大题共4小题,每小题5分,共20分。请把最后结果填在题中横线上)
11.对于任意不相等的两个实数a、b,定义运算※如下:a※b=,如
3※2=,那么8※12= 。
12.已知关于x的不等式组的整数解共有3个,则a的取值范围是 。
13.如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E,则直线CD与⊙O的位置关系是________,阴影部分面积为(结果保留π)________。
14.抛物线y=ax2+bx+c上部分点的横坐标x、纵坐标y的对应值
如下表:
x … 0 1 2 3 4 …
y … -2 -2 0 4 10 …
从上表可知,下列说法中正确的是__________.(填写序号)
① 抛物线与x轴的一个交点坐标为(-1,0); ②在对称轴左侧,y随x的增大而增大;
③抛物线的对称轴是x=; ④函数y=ax2+bx+c的最小值为-2
得分 评卷人 三、(本题共两小题,每小题8分,共16分)
15.解不等式组 ,并把解集在数轴上表示出来.
16.先化简,再求值。
得分 评卷人 四、(本题共两小题,每小题8分,共16分)
17.已知:如图,在 ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG//DB交CB的延长线于G。
(1)求证:
(2)△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论
18.中央电视台举办的第14届“蓝色经典·天之蓝”杯青年歌手大奖赛,由部队文工团的A(海政)、B(空政)、C(武警)组成种子队,由部队文工团的D(解放军)和地方文工团的E(云南)、F(新疆)组成非种子队,现从种子队A、B、C与非种子队D、E、F中各抽取一个队进行首场比赛。
(1)请用适当方式写出首场比赛出场的两个队的所有可能情况(用代码A、B、C、D、E、F表示);
(2)求首场比赛出场的两个队都是部队文工团的概率p。
得分 评卷人 五、(本题共两小题,每小题10分,共20分)
19.某校为了了解学生的学习负担情况,调查了九年级学生每天课外作业所花时间的情况,从每班抽取5名学生作为样本,按A、B、C、D四个类别进行统计。并将统计结果绘制成以下两幅不完整的统计图,请你结合图中信息解答下列问题:(说明:A类:60分钟以下;B类:60分钟—74分钟;C类75分钟—89分钟;D类:90分钟—100分钟)
(1)A类学生的人数为 请补全条形统计图;
(2)扇形统计图中C类学生的人数所占扇形圆心角的度数为 ,D类学生的人数占抽样总人数的百分比为 ;
(3)若该校九年级共有学生500人,请你估计
全年级中A类和B类的学生共有多少人。
20.小刘家准备装修一套新住房,若甲、乙两个装饰公司合作需6周完成,需工钱5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,需工钱4.8万元,若只选一个公司单独完成,从节约开支角度考虑,他家是选甲公司,还是乙公司?请说明理由。
得分 评卷人 六、(本题12分)
21.如图,在Rt△ABC中,∠C=90°,BC=9,CA=12,
∠ABC的平分线BD交AC于点D,DE⊥DB于D,交AB于点E。
(1)设⊙O是△BDE的外接圆,求证AC是⊙O的切线;
(2)设⊙O交BC于点F,连接EF,求的值。
得分 评卷人 七、(本题12分)
22.工艺商场按标价销售某种工艺品,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获得的利润相等。
(1)求该工艺品每件的进价和标价;
(2)若每件该工艺品按(1)中求得的进价进货,按标价销售,那么工艺商场每天可售出该工艺品100件,若每件工艺品每降价1元,则每天便可多售出该工艺品4件,那么每件工艺品降价多少元销售可使每天获得的利润最大?最大利润是多少?
(3)在(2)的情况下,物价部门规定,该商场在该工艺品的经营上每天获得的利润不能超过4800元,而商场在该工艺品的经营中确保每天获得的利润不低于4704元,该工艺品应该如何定价?
得分 评卷人 八、(本题满分14分)
23.如图,抛物线与x轴交于A、B两点,与y轴交于c点,
且A(-1,0)。
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值
数 学
时间:120分钟 满分: 150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
得分 评卷人 一、选择题:(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只一项是符合题目要求的,请将正确选项的序号填写在题后的括号内)
1.9的算术平方根是( )。
A.3 B.-3 C.81 D. -81
2.下列运算正确的是( )。
A. 22.32 =64 B.
C. D.
3.不等式组的解集为( )
A.x>3 B.x≤4 C. 3
A.0.114×105 B.11.4×103 C.1.14×104 D.114×102
5.化简: 的结果是( )。
A.2 B. C. D.
6.若一个菱形的边长为2,则这个菱形两条对角线的平方和为( )。
A.16 B. 8 C.4 D. 1
7.已知∠A是锐角,sinA=,则5cosA=( )。
A.4 B.3 C. D.5
8.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,
若tan∠DBA=,则AD的长为( )。
A.2 B. C. D.1
9.如图,在平面直角坐标系中,⊙p的圆心是(2,a)(a>2),半径为2,函数y=x的图像截⊙p的弦AB的长为,则a的值为( )。
A. B.2+
C. D.2+
10.二次函数y=ax2+bx+c的图像如图所示,则一次函数y=bx+b2-4ac与反比例函数在同一坐标系内的图像大致为( ).
得分 评卷人 二、填空题:(本大题共4小题,每小题5分,共20分。请把最后结果填在题中横线上)
11.对于任意不相等的两个实数a、b,定义运算※如下:a※b=,如
3※2=,那么8※12= 。
12.已知关于x的不等式组的整数解共有3个,则a的取值范围是 。
13.如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E,则直线CD与⊙O的位置关系是________,阴影部分面积为(结果保留π)________。
14.抛物线y=ax2+bx+c上部分点的横坐标x、纵坐标y的对应值
如下表:
x … 0 1 2 3 4 …
y … -2 -2 0 4 10 …
从上表可知,下列说法中正确的是__________.(填写序号)
① 抛物线与x轴的一个交点坐标为(-1,0); ②在对称轴左侧,y随x的增大而增大;
③抛物线的对称轴是x=; ④函数y=ax2+bx+c的最小值为-2
得分 评卷人 三、(本题共两小题,每小题8分,共16分)
15.解不等式组 ,并把解集在数轴上表示出来.
16.先化简,再求值。
得分 评卷人 四、(本题共两小题,每小题8分,共16分)
17.已知:如图,在 ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG//DB交CB的延长线于G。
(1)求证:
(2)△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论
18.中央电视台举办的第14届“蓝色经典·天之蓝”杯青年歌手大奖赛,由部队文工团的A(海政)、B(空政)、C(武警)组成种子队,由部队文工团的D(解放军)和地方文工团的E(云南)、F(新疆)组成非种子队,现从种子队A、B、C与非种子队D、E、F中各抽取一个队进行首场比赛。
(1)请用适当方式写出首场比赛出场的两个队的所有可能情况(用代码A、B、C、D、E、F表示);
(2)求首场比赛出场的两个队都是部队文工团的概率p。
得分 评卷人 五、(本题共两小题,每小题10分,共20分)
19.某校为了了解学生的学习负担情况,调查了九年级学生每天课外作业所花时间的情况,从每班抽取5名学生作为样本,按A、B、C、D四个类别进行统计。并将统计结果绘制成以下两幅不完整的统计图,请你结合图中信息解答下列问题:(说明:A类:60分钟以下;B类:60分钟—74分钟;C类75分钟—89分钟;D类:90分钟—100分钟)
(1)A类学生的人数为 请补全条形统计图;
(2)扇形统计图中C类学生的人数所占扇形圆心角的度数为 ,D类学生的人数占抽样总人数的百分比为 ;
(3)若该校九年级共有学生500人,请你估计
全年级中A类和B类的学生共有多少人。
20.小刘家准备装修一套新住房,若甲、乙两个装饰公司合作需6周完成,需工钱5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,需工钱4.8万元,若只选一个公司单独完成,从节约开支角度考虑,他家是选甲公司,还是乙公司?请说明理由。
得分 评卷人 六、(本题12分)
21.如图,在Rt△ABC中,∠C=90°,BC=9,CA=12,
∠ABC的平分线BD交AC于点D,DE⊥DB于D,交AB于点E。
(1)设⊙O是△BDE的外接圆,求证AC是⊙O的切线;
(2)设⊙O交BC于点F,连接EF,求的值。
得分 评卷人 七、(本题12分)
22.工艺商场按标价销售某种工艺品,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获得的利润相等。
(1)求该工艺品每件的进价和标价;
(2)若每件该工艺品按(1)中求得的进价进货,按标价销售,那么工艺商场每天可售出该工艺品100件,若每件工艺品每降价1元,则每天便可多售出该工艺品4件,那么每件工艺品降价多少元销售可使每天获得的利润最大?最大利润是多少?
(3)在(2)的情况下,物价部门规定,该商场在该工艺品的经营上每天获得的利润不能超过4800元,而商场在该工艺品的经营中确保每天获得的利润不低于4704元,该工艺品应该如何定价?
得分 评卷人 八、(本题满分14分)
23.如图,抛物线与x轴交于A、B两点,与y轴交于c点,
且A(-1,0)。
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值
同课章节目录
