3.4 函数的应用(一)课时训练-2021-2022学年高一上学期数学人教A版(2019)必修第一册(含解析)
文档属性
| 名称 | 3.4 函数的应用(一)课时训练-2021-2022学年高一上学期数学人教A版(2019)必修第一册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 00:00:00 | ||
图片预览




文档简介
2021-2022学年高一数学同步课时训练(人教A版2019必修第一册)
3.4课时
函数的应用(一)
一、单选题。本大题共18小题,每小题只有一个选项符合题意。
1.某厂印刷某图书总成本y(元)与图书日印量x(本)的函数解析式为y=5x+3000,而图书出厂价格为每本10元,则该厂为了不亏本,日印图书至少为( )
A.200本
B.400本
C.600本
D.800本
2.某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是(
)
A.118元
B.105元
C.106元
D.108元
3.面积为的长方形的某边长度为,则该长方形的周长与的函数关系为(
)
A.
B.
C.
D.
4.有一个长方形木块,三个侧面积分别为8,12,24,现将其削成一个正四面体模型,则该正四面体模型棱长的最大值为(
)
A.2
B.
C.4
D.
5.某企业2012年12月份的产值是这年1月份产值的P倍,则该企业2012年度产值的月平均增长率为( )
A.
B.-1
C.
D.
6.某工厂拟建一个平面图形为矩形,且总面积为平方米的三级污水处理池,如图R3-1所示.已知池外墙造价为每米元,中间两条隔墙造价为每米元,池底造价为每平方米元(池壁的厚度忽略不计,且污水处理池无盖).若使污水处理池的总造价最低,那么污水处理池的长和宽分别为
A.米,米
B.米,米
C.米,
米
D.米,米
7.如图,某池塘里浮萍的面积y(单位:)与时间1(单位:月)的关系为.关于下列说法:
①浮萍每月的增长率为1;
②第5个月时,浮萍面积就会超过;
③浮萍每月增加的面积都相等;
④若浮萍蔓延到所经过的时间分别是,则,其中正确的说法是(
)
A.①②
B.①②③
C.①②④
D.①②③④
8.某市出租车起步价为5元(起步价内行驶里程为3
km),以后每1
km价为1.8元(不足1
km按1
km计价),则乘坐出租车的费用y(元)与行驶的里程x(km)之间的函数图像大致为( )
A.B.C.D.
二、多选题。本大题共4小题,每小题有两项或以上符合题意。
9.若函数的图像在R上连续不断,且满足,,,则下列说法错误的是(
)
A.在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点
B.在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点
C.在区间(0,1)上一定有零点,在区间(1,2)上可能有零点
D.在区间(0,1)上可能有零点,在区间(1,2)上一定有零点
10.某公司一年购买某种货物900吨,现分次购买,若每次购买x吨,运费为9万元/次,一年的总储存费用为4x万元,要使一年的总运费与总储存费用之和最小,则下列说法正确的是(
)
A.时费用之和有最小值
B.时费用之和有最小值
C.最小值为万元
D.最小值为万元
11.某市出租车收费标准如下:起步价为8元,起步里程为3km(不超过3km按起步价付费);超过3km但不超过8km时,超过部分按每千米2.15元收费:超过8km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是(
)
A.出租车行驶2km,乘客需付费8元
B.出租车行驶4km,乘客需付费9.6元
C.出租车行驶10km,乘客需付费25.45元
D.某人乘出租车行驶5km两次的费用超过他乘出租车行驶10km一次的费用
E.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9km
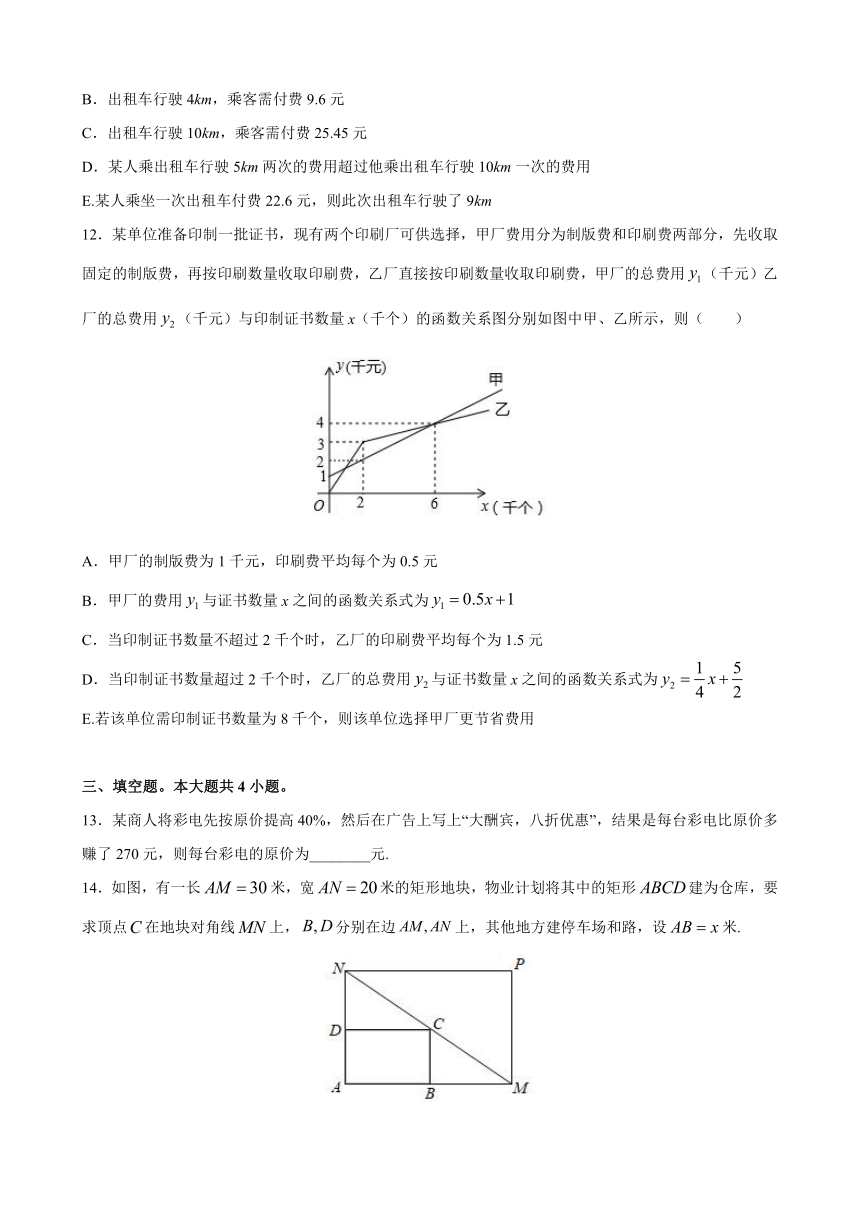
12.某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用(千元)乙厂的总费用(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示,则(
)
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的费用与证书数量x之间的函数关系式为
C.当印制证书数量不超过2千个时,乙厂的印刷费平均每个为1.5元
D.当印制证书数量超过2千个时,乙厂的总费用与证书数量x之间的函数关系式为
E.若该单位需印制证书数量为8千个,则该单位选择甲厂更节省费用
三、填空题。本大题共4小题。
13.某商人将彩电先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果是每台彩电比原价多赚了270元,则每台彩电的原价为________元.
14.如图,有一长米,宽米的矩形地块,物业计划将其中的矩形建为仓库,要求顶点在地块对角线上,分别在边上,其他地方建停车场和路,设米.
则矩形的面积关于的函数解析式为_________.
15.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品万件时的生产成本为
(万元).一万件售价为万元,为获取更大利润,该企业一个月应生产该商品数量为________万件.
16.一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量(辆)与创造的价值(元)之间满足二次函数关系.已知产量为时,创造的价值也为0;当产量为55辆时,创造的价值达到最大6050元.若这家工厂希望利用这条流水线创收达到6000元及以上,则它应该生产的摩托车数量至少是
_____________
;
四、解答题。本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程。
17.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式(可带参数);
(2)假设气体在半径为3
cm的管道中的流量为400
cm3/s,求该气体通过半径为r
cm的管道时,其流量R的表达式;
18.某车间生产一种仪器的固定成本为10
000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数:H(x)=其中x是仪器的月产量.
(1)将利润表示为月产量的函数(用f(x)表示);
(2)当月产量为何值时,车间所获利润最大?最大利润为多少元?(总收入=总成本+利润)
19.某种商品在近30天内每件的销售价格P(元)和时间t(天)的函数关系为:P=
(t∈N
)设该商品的日销售量Q(件)与时间t(天)的函数关系为Q=40-t(0),求这种商品的日销售金额的最大值,并指出日销售金额最大是第几天?
20.某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为(万元).
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
21.经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数(千人)与时间(天)的函数关系近似满足(),人均消费(元)与时间(天)的函数关系近似满足
(1)求该商场的日收益(千元)与时间(天)(,)的函数关系式;
(2)求该商场日收益的最小值(千元).
22.请你设计一个包装盒,如图所示,是边长为的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得、、、四个点重合于图中的点,正好形成一个正四棱柱形状的包装盒,、在上,是被切去的一个等腰直角三角形斜边的两个端点,设.
(1)某广告商要求包装盒的侧面积最大,试问应取何值?
(2)某厂商要求包装盒的容积最大,试问应取何值?
参考答案
1.C
【解析】该厂为了不亏本,日印图书至少为x本,
则利润函数f(x)=10x-(5x+3000)≥0,
解得x≥600.
∴该厂为了不亏本,日印图书至少为600本.
故选C.
2.D
【解析】
设进货价为a元,由题意知132×(1-10%)-a=10%·a,解得a=108,故选D.
3.C
【解析】由条件长方形的一边长度为,且面积为.
则另一边长为,且.
所以该长方形的周长.
故选:C.
4.B
【解析】设长方体从同一顶点出发的三条棱的长分别为,则,故,
若能从该长方体削得一个棱长最长的正四面体模型,
则该四面体的顶点必在长方体的面内,
过正四面体的顶点作垂直于长方体的棱的垂面切割长方体,
含正四面体的几何体必为正方体,
故正四面体的棱长为正方体的面对角线的长,
而从长方体切割出一个正方体,使得面对角线的长最大,
需以最小棱长为切割后的正方体的棱长切割才可,
故所求的正四面体模型棱长的最大值.
故选:B.
5.B
【解析】
设月平均增长率为r,1月份产值为1,则2012年12月的产值为:P=1×(1+r)11,所以(1+r)11=P,即r=
-1,故选B.
6.C
【解析】设污水池的宽为米,则长为米,总造价为,
则(元),
当且仅当时,即当时,总造价最低,
此时,污水池的宽为米,长为米.
故选:C.
7.C
【解析】图象过点
,即
每月的增长率为,①正确;
当时,,②正确;
第二个月比第一个月增加
第三个月比第二个月增加,③错误;
,,
,,
,④正确.
故选:
8.B
【解析】出租车起步价为5元(起步价内行驶的里程是).
对应的值都是5,
以后每价为元,
不足按计价,
时,
时,,故选B.
9.ABD
【解析】由题知,所以根据函数零点存在定理可得在区间上一定有零点,
又,无法判断在区间上是否有零点,在区间(1,2)上可能有零点.
故选:.
10.BD
【解析】一年购买某种货物900吨,若每次购买x吨,则需要购买次,运费是9万元/次,
一年的总储存费用为万元,
所以一年的总运费与总储存费用之和为,
因为,
当且仅当,即时,等号成立,
所以当时,一年的总运费与总储存费用之和最小为万元,
故选:BD
11.CDE
【解析】解:在中,出租车行驶2km,乘客需付起步价8元和燃油附加费1元,共9元,错误;在中,出租车行驶4km,乘客需付费元,错误;
在中,出租车行驶10km,乘客需付费元,正确;
在中,乘出租车行驶5km,乘客需付费元,乘坐两次需付费26.6元,,正确;
在中,设出租车行驶时,付费元,由知,因此由,解得,正确.
故选:.
12.ABCD
【解析】由题图知甲厂制版费为1千元,印刷费平均每个为0.5元,故A正确;
甲厂的费用与证书数量x满足的函数关系为,故B正确;
当印制证书数量不超过2千个时,乙厂的印刷费平均每个为元,故C正确;
易知当时,与x之间的函数关系式为,故D正确
当时,,因为,所以当印制8千个证书时,选择乙厂更节省费用,故E不正确.
故选ABCD
13.2250
【解析】设彩电的原价为a元,∴a(1+40%)·80%-a=270,∴0.12a=270,解得a=2
250.
∴每台彩电的原价为2
250元.
故答案为:2250.
14.
【解析】解:在直角中,
所以,
∴,
∴,
所以矩形的面积关于的函数解析式为.
15.
【解析】设利润为,则,当时,有最大值,
故答案为:18.
16.50辆
【解析】由题意,设摩托车数量(辆)与创造的价值(元)之间满足二次函数,又,故,则,解得,
故答案为50辆
17.(1);(2).
【解析】(1)由于流量R与管道半径r的四次方成正比,所以函数解析式为.
(2)由r=3
cm,R=400
cm3/s,得k·34=400,∴,∴流量R的表达式为.
18.(1);(2)每月生产150台仪器时,利润最大,最大利润为12
500元.
【解析】(1)设每月产量为台,则总成本为.又,
(2)当时,,所以当时,有最大值12
500;
当时,是减函数,.
所以当时,f(x)取最大值,最大值为12
500.
所以每月生产150台仪器时,利润最大,最大利润为12
500元.
19.销售额的最大值为1125元,且在第25天时日销售金额达到最大.
【解析】设日销售金额为元,则
,
即,
当时,,时有最大值900;
当时,是减函数,时有最大值1125.
综上所述,时有最大值1125,
所以,第25天日销售金额最大,最大值为1125元.
20.(1)f(x)=;(2)475件.
【解析】(1)当05时,产品只能售出500件.
所以,
即f(x)=.
(2)当0所以当x=4.75(百件)时,f(x)有最大值,
f(x)max=10.781
25(万元).
当x>5时,f(x)<12-0.25×5=10.75(万元).
故当年产量为475件时,当年所得利润最大.
21.(1);(2)千元
【解析】(1)根据该商场的日收益=顾客人数×人均消费的钱数得w(t)与t的解析式;(2)根据第一问得到w(t)为分段函数,分别求出各段的最值,第一段运用基本不等式求出最值,第二段是一个递减的一次函数求出最值比较即可
(1)
(2)时,单调递增,最小值在处取到,;
时,单调递减,最小值在时取到,
单调递减,最小值在时取到,则最小值为,
由,可得最小值为.
答:该商场日收益的最小值为千元.
22.(1);(2).
【解析】(1)设包装盒的底面边长为,高为,
则由题意可得,,,其中,
所以,
因此,当时,取得最大值;
(2)根据题意,由(1)有,
,由由得,(舍)或.
当时,;当时,.
所以,函数在区间上单调递增,在区间上单调递减,
所以,当时,函数取得极大值,也是最大值.
3.4课时
函数的应用(一)
一、单选题。本大题共18小题,每小题只有一个选项符合题意。
1.某厂印刷某图书总成本y(元)与图书日印量x(本)的函数解析式为y=5x+3000,而图书出厂价格为每本10元,则该厂为了不亏本,日印图书至少为( )
A.200本
B.400本
C.600本
D.800本
2.某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是(
)
A.118元
B.105元
C.106元
D.108元
3.面积为的长方形的某边长度为,则该长方形的周长与的函数关系为(
)
A.
B.
C.
D.
4.有一个长方形木块,三个侧面积分别为8,12,24,现将其削成一个正四面体模型,则该正四面体模型棱长的最大值为(
)
A.2
B.
C.4
D.
5.某企业2012年12月份的产值是这年1月份产值的P倍,则该企业2012年度产值的月平均增长率为( )
A.
B.-1
C.
D.
6.某工厂拟建一个平面图形为矩形,且总面积为平方米的三级污水处理池,如图R3-1所示.已知池外墙造价为每米元,中间两条隔墙造价为每米元,池底造价为每平方米元(池壁的厚度忽略不计,且污水处理池无盖).若使污水处理池的总造价最低,那么污水处理池的长和宽分别为
A.米,米
B.米,米
C.米,
米
D.米,米
7.如图,某池塘里浮萍的面积y(单位:)与时间1(单位:月)的关系为.关于下列说法:
①浮萍每月的增长率为1;
②第5个月时,浮萍面积就会超过;
③浮萍每月增加的面积都相等;
④若浮萍蔓延到所经过的时间分别是,则,其中正确的说法是(
)
A.①②
B.①②③
C.①②④
D.①②③④
8.某市出租车起步价为5元(起步价内行驶里程为3
km),以后每1
km价为1.8元(不足1
km按1
km计价),则乘坐出租车的费用y(元)与行驶的里程x(km)之间的函数图像大致为( )
A.B.C.D.
二、多选题。本大题共4小题,每小题有两项或以上符合题意。
9.若函数的图像在R上连续不断,且满足,,,则下列说法错误的是(
)
A.在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点
B.在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点
C.在区间(0,1)上一定有零点,在区间(1,2)上可能有零点
D.在区间(0,1)上可能有零点,在区间(1,2)上一定有零点
10.某公司一年购买某种货物900吨,现分次购买,若每次购买x吨,运费为9万元/次,一年的总储存费用为4x万元,要使一年的总运费与总储存费用之和最小,则下列说法正确的是(
)
A.时费用之和有最小值
B.时费用之和有最小值
C.最小值为万元
D.最小值为万元
11.某市出租车收费标准如下:起步价为8元,起步里程为3km(不超过3km按起步价付费);超过3km但不超过8km时,超过部分按每千米2.15元收费:超过8km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是(
)
A.出租车行驶2km,乘客需付费8元
B.出租车行驶4km,乘客需付费9.6元
C.出租车行驶10km,乘客需付费25.45元
D.某人乘出租车行驶5km两次的费用超过他乘出租车行驶10km一次的费用
E.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9km
12.某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费,甲厂的总费用(千元)乙厂的总费用(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示,则(
)
A.甲厂的制版费为1千元,印刷费平均每个为0.5元
B.甲厂的费用与证书数量x之间的函数关系式为
C.当印制证书数量不超过2千个时,乙厂的印刷费平均每个为1.5元
D.当印制证书数量超过2千个时,乙厂的总费用与证书数量x之间的函数关系式为
E.若该单位需印制证书数量为8千个,则该单位选择甲厂更节省费用
三、填空题。本大题共4小题。
13.某商人将彩电先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果是每台彩电比原价多赚了270元,则每台彩电的原价为________元.
14.如图,有一长米,宽米的矩形地块,物业计划将其中的矩形建为仓库,要求顶点在地块对角线上,分别在边上,其他地方建停车场和路,设米.
则矩形的面积关于的函数解析式为_________.
15.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品万件时的生产成本为
(万元).一万件售价为万元,为获取更大利润,该企业一个月应生产该商品数量为________万件.
16.一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量(辆)与创造的价值(元)之间满足二次函数关系.已知产量为时,创造的价值也为0;当产量为55辆时,创造的价值达到最大6050元.若这家工厂希望利用这条流水线创收达到6000元及以上,则它应该生产的摩托车数量至少是
_____________
;
四、解答题。本大题共6小题,解答过程必修有必要的文字说明,公式和解题过程。
17.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式(可带参数);
(2)假设气体在半径为3
cm的管道中的流量为400
cm3/s,求该气体通过半径为r
cm的管道时,其流量R的表达式;
18.某车间生产一种仪器的固定成本为10
000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数:H(x)=其中x是仪器的月产量.
(1)将利润表示为月产量的函数(用f(x)表示);
(2)当月产量为何值时,车间所获利润最大?最大利润为多少元?(总收入=总成本+利润)
19.某种商品在近30天内每件的销售价格P(元)和时间t(天)的函数关系为:P=
(t∈N
)设该商品的日销售量Q(件)与时间t(天)的函数关系为Q=40-t(0
20.某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为(万元).
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
21.经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数(千人)与时间(天)的函数关系近似满足(),人均消费(元)与时间(天)的函数关系近似满足
(1)求该商场的日收益(千元)与时间(天)(,)的函数关系式;
(2)求该商场日收益的最小值(千元).
22.请你设计一个包装盒,如图所示,是边长为的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得、、、四个点重合于图中的点,正好形成一个正四棱柱形状的包装盒,、在上,是被切去的一个等腰直角三角形斜边的两个端点,设.
(1)某广告商要求包装盒的侧面积最大,试问应取何值?
(2)某厂商要求包装盒的容积最大,试问应取何值?
参考答案
1.C
【解析】该厂为了不亏本,日印图书至少为x本,
则利润函数f(x)=10x-(5x+3000)≥0,
解得x≥600.
∴该厂为了不亏本,日印图书至少为600本.
故选C.
2.D
【解析】
设进货价为a元,由题意知132×(1-10%)-a=10%·a,解得a=108,故选D.
3.C
【解析】由条件长方形的一边长度为,且面积为.
则另一边长为,且.
所以该长方形的周长.
故选:C.
4.B
【解析】设长方体从同一顶点出发的三条棱的长分别为,则,故,
若能从该长方体削得一个棱长最长的正四面体模型,
则该四面体的顶点必在长方体的面内,
过正四面体的顶点作垂直于长方体的棱的垂面切割长方体,
含正四面体的几何体必为正方体,
故正四面体的棱长为正方体的面对角线的长,
而从长方体切割出一个正方体,使得面对角线的长最大,
需以最小棱长为切割后的正方体的棱长切割才可,
故所求的正四面体模型棱长的最大值.
故选:B.
5.B
【解析】
设月平均增长率为r,1月份产值为1,则2012年12月的产值为:P=1×(1+r)11,所以(1+r)11=P,即r=
-1,故选B.
6.C
【解析】设污水池的宽为米,则长为米,总造价为,
则(元),
当且仅当时,即当时,总造价最低,
此时,污水池的宽为米,长为米.
故选:C.
7.C
【解析】图象过点
,即
每月的增长率为,①正确;
当时,,②正确;
第二个月比第一个月增加
第三个月比第二个月增加,③错误;
,,
,,
,④正确.
故选:
8.B
【解析】出租车起步价为5元(起步价内行驶的里程是).
对应的值都是5,
以后每价为元,
不足按计价,
时,
时,,故选B.
9.ABD
【解析】由题知,所以根据函数零点存在定理可得在区间上一定有零点,
又,无法判断在区间上是否有零点,在区间(1,2)上可能有零点.
故选:.
10.BD
【解析】一年购买某种货物900吨,若每次购买x吨,则需要购买次,运费是9万元/次,
一年的总储存费用为万元,
所以一年的总运费与总储存费用之和为,
因为,
当且仅当,即时,等号成立,
所以当时,一年的总运费与总储存费用之和最小为万元,
故选:BD
11.CDE
【解析】解:在中,出租车行驶2km,乘客需付起步价8元和燃油附加费1元,共9元,错误;在中,出租车行驶4km,乘客需付费元,错误;
在中,出租车行驶10km,乘客需付费元,正确;
在中,乘出租车行驶5km,乘客需付费元,乘坐两次需付费26.6元,,正确;
在中,设出租车行驶时,付费元,由知,因此由,解得,正确.
故选:.
12.ABCD
【解析】由题图知甲厂制版费为1千元,印刷费平均每个为0.5元,故A正确;
甲厂的费用与证书数量x满足的函数关系为,故B正确;
当印制证书数量不超过2千个时,乙厂的印刷费平均每个为元,故C正确;
易知当时,与x之间的函数关系式为,故D正确
当时,,因为,所以当印制8千个证书时,选择乙厂更节省费用,故E不正确.
故选ABCD
13.2250
【解析】设彩电的原价为a元,∴a(1+40%)·80%-a=270,∴0.12a=270,解得a=2
250.
∴每台彩电的原价为2
250元.
故答案为:2250.
14.
【解析】解:在直角中,
所以,
∴,
∴,
所以矩形的面积关于的函数解析式为.
15.
【解析】设利润为,则,当时,有最大值,
故答案为:18.
16.50辆
【解析】由题意,设摩托车数量(辆)与创造的价值(元)之间满足二次函数,又,故,则,解得,
故答案为50辆
17.(1);(2).
【解析】(1)由于流量R与管道半径r的四次方成正比,所以函数解析式为.
(2)由r=3
cm,R=400
cm3/s,得k·34=400,∴,∴流量R的表达式为.
18.(1);(2)每月生产150台仪器时,利润最大,最大利润为12
500元.
【解析】(1)设每月产量为台,则总成本为.又,
(2)当时,,所以当时,有最大值12
500;
当时,是减函数,.
所以当时,f(x)取最大值,最大值为12
500.
所以每月生产150台仪器时,利润最大,最大利润为12
500元.
19.销售额的最大值为1125元,且在第25天时日销售金额达到最大.
【解析】设日销售金额为元,则
,
即,
当时,,时有最大值900;
当时,是减函数,时有最大值1125.
综上所述,时有最大值1125,
所以,第25天日销售金额最大,最大值为1125元.
20.(1)f(x)=;(2)475件.
【解析】(1)当0
所以,
即f(x)=.
(2)当0
f(x)max=10.781
25(万元).
当x>5时,f(x)<12-0.25×5=10.75(万元).
故当年产量为475件时,当年所得利润最大.
21.(1);(2)千元
【解析】(1)根据该商场的日收益=顾客人数×人均消费的钱数得w(t)与t的解析式;(2)根据第一问得到w(t)为分段函数,分别求出各段的最值,第一段运用基本不等式求出最值,第二段是一个递减的一次函数求出最值比较即可
(1)
(2)时,单调递增,最小值在处取到,;
时,单调递减,最小值在时取到,
单调递减,最小值在时取到,则最小值为,
由,可得最小值为.
答:该商场日收益的最小值为千元.
22.(1);(2).
【解析】(1)设包装盒的底面边长为,高为,
则由题意可得,,,其中,
所以,
因此,当时,取得最大值;
(2)根据题意,由(1)有,
,由由得,(舍)或.
当时,;当时,.
所以,函数在区间上单调递增,在区间上单调递减,
所以,当时,函数取得极大值,也是最大值.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
