四川省乐山市2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 四川省乐山市2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 851.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 14:35:48 | ||
图片预览



文档简介
乐山市高中2023届期末教学质量检测
数 学
(试卷满分:150分 考试时间:120分钟)
本试题卷分第一部分(选择题)和第二部分(非选择题)两部分.第一部分1至2页,第二部分3至4页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分,考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.
第一部分(选择题 共60分)
注意事项:
1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3. 考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. ,的等差中项是( )
A. B. C. 1 D. 2
2. ( )
A. B. C. D.
3. 如图,、、分别是等边各边的中点,则下列结论成立的是( )
A. B.
C. D.
4. 设,,则有( )
A. B. C. D.
5. 设是非零向量,是非零实数,下列结论正确的是( )
A. 与的方向相同 B. 与的方向相反
C. D.
6. ,下列命题正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
7. 在等差数列中,若,则( )
A. 18 B. 30 C. 36 D. 72
8. 在中,,分别是角,的对边,若成立,那么的形状是( )
A. 直角三角形 B. 等腰三角形
C. 等腰或直角三角形 D. 无法判断
9. 在中,角、、所对的边分别是,,,且,则( )
A. B. C. D.
10. 已知数列中,,若,且、、三点共线(该直线不过点),则数列的通项公式为( )
A. B.
C. D.
11. 如图,四边形是等腰梯形,、分别是腰、的中点,点是的一个三分点,,若,则( )
A. B.
C. D.
12. 已知正项等比数列满足,若存在两项,,使得成立,则的最小值为( )
A. B. C. D. 不存在
第二部分(非选择题 90分)
注意事项:
1. 考生须用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答,作图题可先用铅笔画线,确认后用0.5毫米黑色墨迹签字笔描清楚,答在试题卷上无效.
2. 本部分共10小题,共90分.
二、填空题:本大题共4小题;每小题5分,共 20分.
13. 不等式的解集为__________.
14. 已知,,,如果,则__________.
15. 某市出租车的计价标准为1.2元,起步价为6元,即最初(不含)计费6元.若某人乘坐该市的出租车去往处的目的地,且一路畅通,等候时间为0,那么他需要支付的车费为___________.
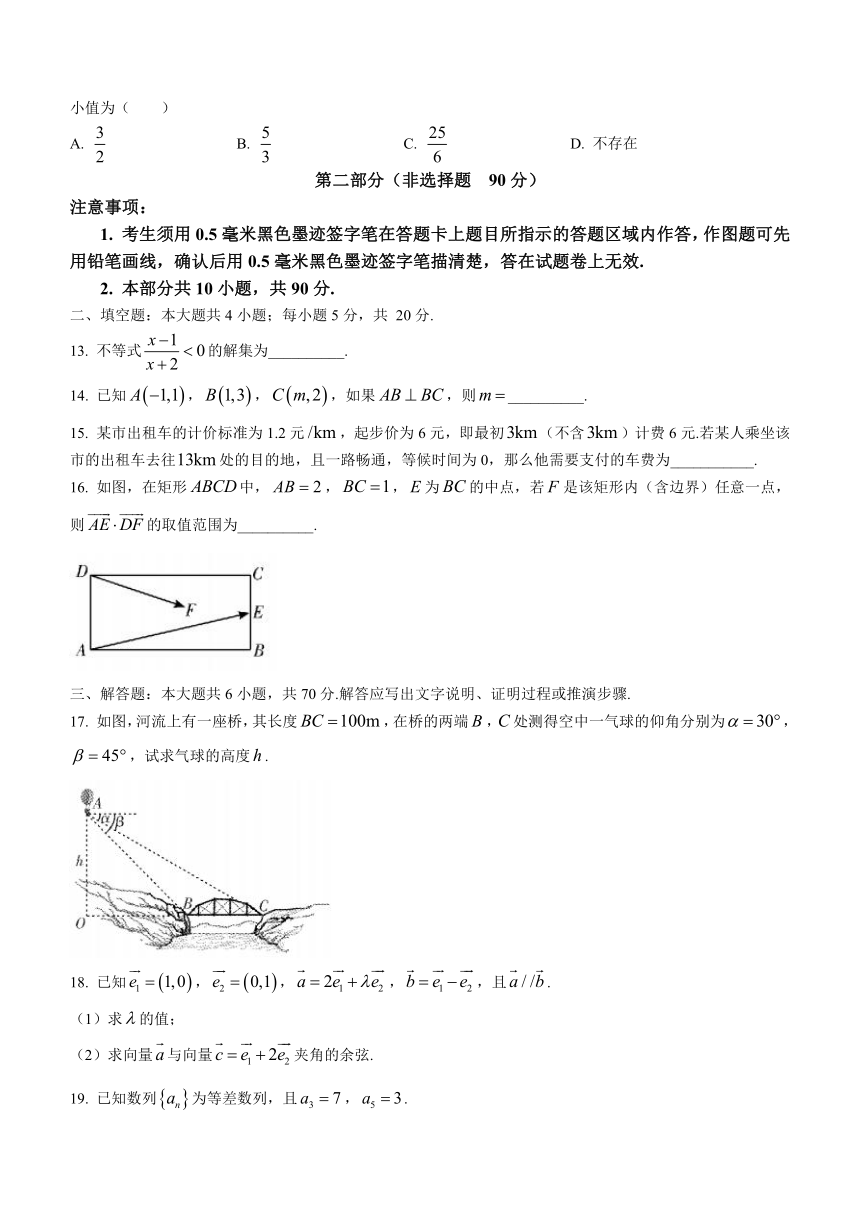
16. 如图,在矩形中,,,为的中点,若是该矩形内(含边界)任意一点,则的取值范围为__________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或推演步骤.
17. 如图,河流上有一座桥,其长度,在桥的两端,处测得空中一气球的仰角分别为,,试求气球的高度.
18. 已知,,,,且.
(1)求的值;
(2)求向量与向量夹角的余弦.
19. 已知数列为等差数列,且,.
(1)求数列的通项公式;
(2)求数列的前项和的最大值.
20. 某地要修建一条大型输油管道通过宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的费用为400元,铺设距离为的相邻两增压站之间的输油管道费用为万元.设余下工程的总费用为(万元).
(1)试将表示为的函数;
(2)需要修建多少个增压站才能使最小,其最小值为多少?
21. 如图,在平面直角坐标系中,角的顶点在原点,始边与轴的非负半轴重合,终边交单位圆于点,且,将角的终边绕原点逆时针方向旋转,交单位圆于点,过作轴于点.
(1)若点的纵坐标为,求点的横坐标;
(2)求的面积的最大值.
22. 已知单调等比数列中,首项,其前项和为,且,,成等差数列,数列满足条件.
(1)求数列,的通项公式;
(2)设,记数列的前项和为.
①求;
②求正整数,使得对任意,均有.
乐山市高中2023届教学质量检测
数学参考答案及评分意见
2021.7
一、选择题(每小题5分,12小题,共60分)
1-5:ABBCD 6-10:CCCBA 11-12:DA
二、填空题(每小题5分,4小题,共计20分)
13. 14. 2 15. 19.2 16.
三、解答题(6小题,共70分)
17. 解:由题可知,,
,
∴,
∴,
在中,∵,
∴,
即.
答:气球的高度为.
18. 解:(1)由题知
,
,
∵,∴,
∴,
(2)由(1)知,,
令与的夹角为,
∴
.
19. 解:因为为等差数列,令其公差为,
则由题意得,
得,
故
,
即的通项公式为.
(2)由(1)知,,
故
,
所以当,的最大值为.
20. 解:(1)设需要修建个增压站,
则,即,
则
.
因为相邻两个增压站之间的距离,
所以,故与的函数关系为
.
(2),
当且仅当,
即时等号成立.
此时,
故需要修建11个增压站才能使最小,其最小值为9440万元.
21. 解:(1)由定义得:,
,
依题意可知,,因为,
所以,
所以点的横坐标为.
(2)因为,,
,
所以
.
又,所以,
所以当,
则时,取得最大值,
所以的最大值为.
22. 解:(1)设,由已知得
,
即,
∴,
∴,
即,则,
由已知数列是单调等比数列,且,
∴,
数列的通项公式为,
∵,
∴,
即.
(2)由(1)得,
①设,的前项和为,则
,
又设,的前项和为,
则
,
∴
;
②令
,
由于比变化快,
∴令,得,
即,,,递增,而,,…递减,
∴最大,即当时,.
数 学
(试卷满分:150分 考试时间:120分钟)
本试题卷分第一部分(选择题)和第二部分(非选择题)两部分.第一部分1至2页,第二部分3至4页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分,考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.
第一部分(选择题 共60分)
注意事项:
1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3. 考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. ,的等差中项是( )
A. B. C. 1 D. 2
2. ( )
A. B. C. D.
3. 如图,、、分别是等边各边的中点,则下列结论成立的是( )
A. B.
C. D.
4. 设,,则有( )
A. B. C. D.
5. 设是非零向量,是非零实数,下列结论正确的是( )
A. 与的方向相同 B. 与的方向相反
C. D.
6. ,下列命题正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
7. 在等差数列中,若,则( )
A. 18 B. 30 C. 36 D. 72
8. 在中,,分别是角,的对边,若成立,那么的形状是( )
A. 直角三角形 B. 等腰三角形
C. 等腰或直角三角形 D. 无法判断
9. 在中,角、、所对的边分别是,,,且,则( )
A. B. C. D.
10. 已知数列中,,若,且、、三点共线(该直线不过点),则数列的通项公式为( )
A. B.
C. D.
11. 如图,四边形是等腰梯形,、分别是腰、的中点,点是的一个三分点,,若,则( )
A. B.
C. D.
12. 已知正项等比数列满足,若存在两项,,使得成立,则的最小值为( )
A. B. C. D. 不存在
第二部分(非选择题 90分)
注意事项:
1. 考生须用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答,作图题可先用铅笔画线,确认后用0.5毫米黑色墨迹签字笔描清楚,答在试题卷上无效.
2. 本部分共10小题,共90分.
二、填空题:本大题共4小题;每小题5分,共 20分.
13. 不等式的解集为__________.
14. 已知,,,如果,则__________.
15. 某市出租车的计价标准为1.2元,起步价为6元,即最初(不含)计费6元.若某人乘坐该市的出租车去往处的目的地,且一路畅通,等候时间为0,那么他需要支付的车费为___________.
16. 如图,在矩形中,,,为的中点,若是该矩形内(含边界)任意一点,则的取值范围为__________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或推演步骤.
17. 如图,河流上有一座桥,其长度,在桥的两端,处测得空中一气球的仰角分别为,,试求气球的高度.
18. 已知,,,,且.
(1)求的值;
(2)求向量与向量夹角的余弦.
19. 已知数列为等差数列,且,.
(1)求数列的通项公式;
(2)求数列的前项和的最大值.
20. 某地要修建一条大型输油管道通过宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的费用为400元,铺设距离为的相邻两增压站之间的输油管道费用为万元.设余下工程的总费用为(万元).
(1)试将表示为的函数;
(2)需要修建多少个增压站才能使最小,其最小值为多少?
21. 如图,在平面直角坐标系中,角的顶点在原点,始边与轴的非负半轴重合,终边交单位圆于点,且,将角的终边绕原点逆时针方向旋转,交单位圆于点,过作轴于点.
(1)若点的纵坐标为,求点的横坐标;
(2)求的面积的最大值.
22. 已知单调等比数列中,首项,其前项和为,且,,成等差数列,数列满足条件.
(1)求数列,的通项公式;
(2)设,记数列的前项和为.
①求;
②求正整数,使得对任意,均有.
乐山市高中2023届教学质量检测
数学参考答案及评分意见
2021.7
一、选择题(每小题5分,12小题,共60分)
1-5:ABBCD 6-10:CCCBA 11-12:DA
二、填空题(每小题5分,4小题,共计20分)
13. 14. 2 15. 19.2 16.
三、解答题(6小题,共70分)
17. 解:由题可知,,
,
∴,
∴,
在中,∵,
∴,
即.
答:气球的高度为.
18. 解:(1)由题知
,
,
∵,∴,
∴,
(2)由(1)知,,
令与的夹角为,
∴
.
19. 解:因为为等差数列,令其公差为,
则由题意得,
得,
故
,
即的通项公式为.
(2)由(1)知,,
故
,
所以当,的最大值为.
20. 解:(1)设需要修建个增压站,
则,即,
则
.
因为相邻两个增压站之间的距离,
所以,故与的函数关系为
.
(2),
当且仅当,
即时等号成立.
此时,
故需要修建11个增压站才能使最小,其最小值为9440万元.
21. 解:(1)由定义得:,
,
依题意可知,,因为,
所以,
所以点的横坐标为.
(2)因为,,
,
所以
.
又,所以,
所以当,
则时,取得最大值,
所以的最大值为.
22. 解:(1)设,由已知得
,
即,
∴,
∴,
即,则,
由已知数列是单调等比数列,且,
∴,
数列的通项公式为,
∵,
∴,
即.
(2)由(1)得,
①设,的前项和为,则
,
又设,的前项和为,
则
,
∴
;
②令
,
由于比变化快,
∴令,得,
即,,,递增,而,,…递减,
∴最大,即当时,.
同课章节目录
