第3章专题8 函数的奇偶性-【新教材】人教A版(2019)高中数学必修第一册常考题型专题练习(机构专用)(Word版含解析)
文档属性
| 名称 | 第3章专题8 函数的奇偶性-【新教材】人教A版(2019)高中数学必修第一册常考题型专题练习(机构专用)(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 278.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 08:14:45 | ||
图片预览




文档简介
函数的奇偶性
考向一 函数奇偶性的判断
1、下列函数中,是奇函数的为(??? ).
A.false B.false C.false D.false
2、判断下列函数的奇偶性:
(1)f(x)=false+false;
(2)f(x)=false
3、判断函数f(x)={x2?2x+5,(x>0)1,(x=0)?x2?2x?5,(x<0)的奇偶性.
4、已知函数 y=f(x)(x≠0) 对于任意的 x,y∈R 且 x,y≠0 都满足 f(xy)=f(x)+f(y).
(1) 求 f(1),f(?1) 的值;
(2) 判断函数 y=f(x)(x≠0) 的奇偶性.
5、函数 f(x),x∈R,若对于任意实数 a,b,都有 f(a+b)=f(a)+f(b),求证:f(x) 为奇函数.
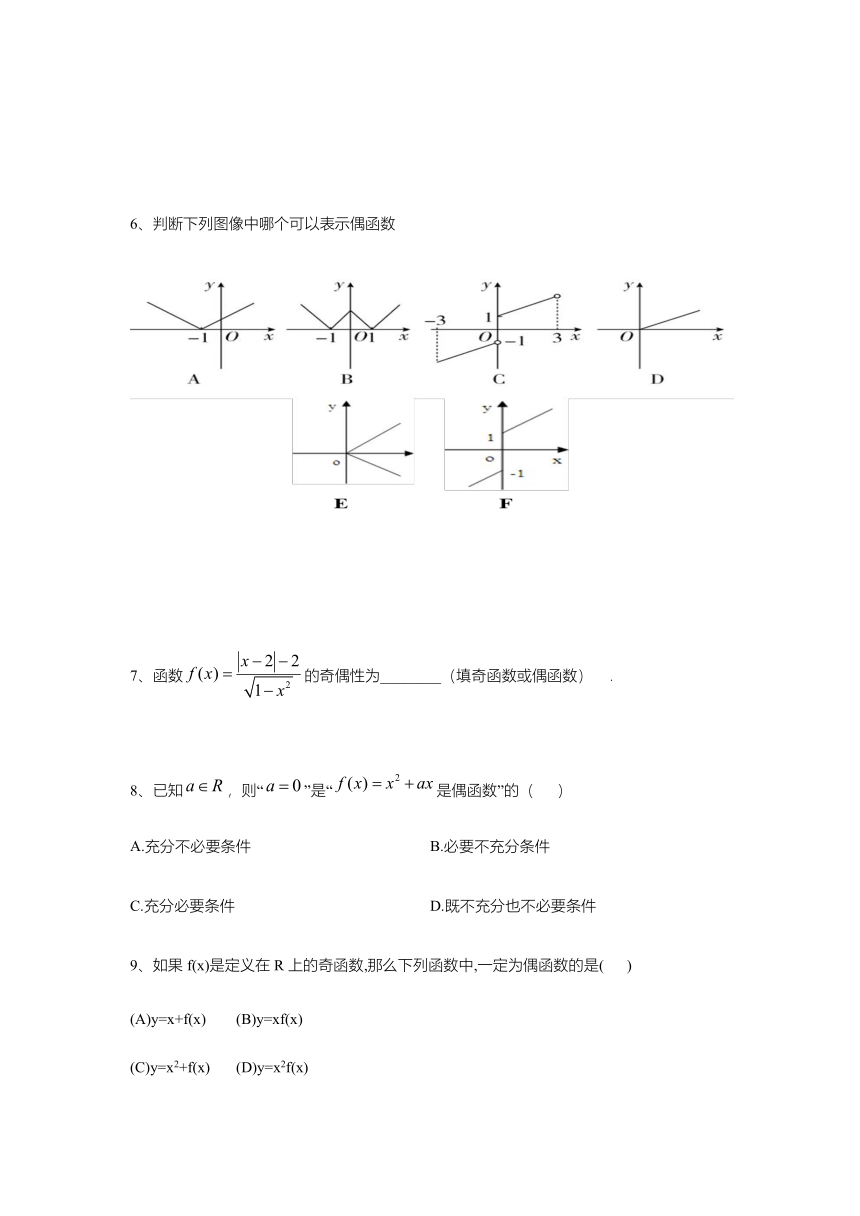
6、判断下列图像中哪个可以表示偶函数
7、函数false的奇偶性为________(填奇函数或偶函数) .
8、已知false,则“false”是“false是偶函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
9、如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是( )
(A)y=x+f(x) (B)y=xf(x)
(C)y=x2+f(x) (D)y=x2f(x)
考向二 奇偶性的性质
1、偶函数false在区间false上的图象如图,则函数false的增区间为______________.
2、已知函数false.
(1)判断false的奇偶性,由此作出false的大致图象;
(2)求false的值域和单调区间.
考向三 根据函数的奇偶性求参数的值
1、若函数false是偶函数,则false等于____.
2、已知 f(x)=ax2+bx 是定义在 [a?1,2a] 上的偶函数,那么 a+b 的值是( )
A.?13 B.13C.12 D.?12
3、若函数false在false上是奇函数,则false的解析式为( ).
A.false B.false
C.false D.false
4、已知函数f(x)=false为定义是区间[-2a,3a-1]上的奇函数,则a+b=________.
考向四 根据奇偶性求函数值或解析式
1、如图,给出奇函数false的局部图象,则false的值为( )
A.false B.2 C.1 D.0
2、已知函数false为奇函数,若false,则false .
3、已知 f(x) 是定义在 R 上的奇函数,当x≥0 时, f(x)=x2?2x ,则 f(x) 在R 上的表达式为( )
A.f(x)=x(x?2) B.f(x)=x(|x|?1) C.f(x)=|x|(x?2) D.f(x)=x(|x|?2)
4、已知定义在 R 上的奇函数 f(x),当 x>0 时,f(x)=x2+|x|?x,那么 x<0 时,f(x)= ________
5、已知false是偶函数,false是奇函数,若false,则false的解析式为_______.
函数的奇偶性
考向一 函数奇偶性的判断
1、下列函数中,是奇函数的为(??? ).
A.false B.false C.false D.false
【答案】A
【解析】对函数false,由于false,因此false,定义域为false,false,因此false为奇函数.
故选A.
2、判断下列函数的奇偶性:
(1)f(x)=false+false;
(2)f(x)=false
【解析】(1)由false得x2=3,解得x=±false,
即函数f(x)的定义域为{-false,false},
从而f(x)=false+false=0.
因此f(-x)=-f(x)且f(-x)=f(x),
∴函数f(x)既是奇函数又是偶函数.
(2)显然函数f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称.
∵当x<0时,-x>0,
则f(-x)=-(-x)2-x=-x2-x=-f(x);
当x>0时,-x<0,
则f(-x)=(-x)2-x=x2-x=-f(x);
综上可知:对于定义域内的任意x,总有f(-x)=-f(x)成立,∴函数f(x)为奇函数.
3、判断函数f(x)={x2?2x+5,(x>0)1,(x=0)?x2?2x?5,(x<0)的奇偶性.
【答案】非奇非偶函数
【解析】1.先判断函数的定义域为R,所以是关于原点对称2.不妨设x>0,则f(x)=x2?2x+5,同时会有?x<0,则有f(?x)=?(?x)2+2x?5=?x2+2x?5=?f(x)3.因为f(0)≠0,所以函数是非奇非偶函数。
4、已知函数 y=f(x)(x≠0) 对于任意的 x,y∈R 且 x,y≠0 都满足 f(xy)=f(x)+f(y).
(1) 求 f(1),f(?1) 的值;
【答案】f(1)=0,f(?1)=0
【解析】令 x=y=1 即可得 f(1),令 x=y=?1 即可得 f(?1)=0.因为对于任意的 x,y∈R 且 x,y≠0 都满足 f(xy)=f(x)+f(y).所以令 x=y=1,得到 f(1)=f(1)+f(1).所以 f(1)=0.令 x=y=?1,得到 f(1)=f(?1)+f(?1).所以 f(?1)=0.
(2) 判断函数 y=f(x)(x≠0) 的奇偶性.
【答案】偶函数
【解析】令 y=?1,得 f(xy)=f(?x)=f(x)+f(?1),由 (1) 可得偶函数.由题意可知,函数 y=f(x) 的定义域为 (?∞,0)∪(0,+∞),关于原点对称.令 y=?1,得 f(xy)=f(?x)=f(x)+f(?1).因为 f(?1)=0.所以 f(?x)=f(x).所以 y=f(x)(x≠0) 为偶函数.
5、函数 f(x),x∈R,若对于任意实数 a,b,都有 f(a+b)=f(a)+f(b),求证:f(x) 为奇函数.
【答案】略
【解析】由于对任意的 x∈(?l,l) 也必有 ?x∈(?l,l),可见,f(?x) 的定义域也是 (?l,l).若设 F(x)=f(x)+f(?x),G(x)=f(x)?f(?x),则 F(x) 与 G(x) 的定义域都是 (?l,l),显然是关于原点对称的区间.而且 F(?x)=f(?x)+f[?(?x)]=f(x)+f(?x)=F(x),故 F(x) 为偶函数. G(?x)=f(?x)?f[?(?x)]=f(?x)?f(x)=?[f(x)?f(?x)]=?G(x),故 G(x) 为奇函数.
6、判断下列图像中哪个可以表示偶函数
【答案】B
【解析】A虽然是轴对称图像,但对称轴不是y轴,所以不是偶函数图像,当然也不是奇函数图像;B关于y轴对称,是偶函数图像;C乍一看上去是中心对称图像,但是要注意,对称性是对图像上任意的一点都满足,x=0和x=3或x=?3时并不满足,所以不是奇函数;D选项最明显,不是奇函数图像也不是偶函数图像;E不关于y轴对称,也不关于原点对称,不是奇函数也不是偶函数;F:首先图像必须为函数图像(回忆函数定义),x=0处对应两个函数值,并不是函数图像,所以F不表示奇偶函数图像.
7、函数false的奇偶性为________(填奇函数或偶函数) .
【答案】奇函数
【解析】
由已知得false 的定义域为false 即false ,则falsefalse 其定义域关于原点对称,false ,所以false 是奇函数.
8、已知false,则“false”是“false是偶函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】C
【解析】
因为false是偶函数,所以false
所以false.所以“false”是“false是偶函数”的充要条件.故选C.
9、如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是( )
(A)y=x+f(x) (B)y=xf(x)
(C)y=x2+f(x) (D)y=x2f(x)
【答案】B
【解析】因为f(x)是奇函数,所以f(-x)=-f(x).
对于A,g(-x)=-x+f(-x)=-x-f(x)=-g(x),所以y=x+f(x)是奇函数.
对于B,g(-x)=-xf(-x)=xf(x)=g(x),所以y=xf(x)是偶函数.
对于C,g(-x)=(-x)2+f(-x)=x2-f(x),所以y=x2+f(x)为非奇非偶函数,
对于D,g(-x)=(-x)2f(-x)=-x2f(x)=-g(x),所以y=x2f(x)是奇函数.故选B.
考向二 奇偶性的性质
1、偶函数false在区间false上的图象如图,则函数false的增区间为______________.
【答案】false和false
【解析】偶函数的图象关于false轴对称,可知函数false的增区间为false和false
2、已知函数false.
(1)判断false的奇偶性,由此作出false的大致图象;
(2)求false的值域和单调区间.
【答案】(1)偶函数,图象见解析;(2)值域为false,增区间为false和false,减区间为false和false.
【解析】(1)对于函数false,false,解得false,
所以,函数false的定义域为false,
又false,所以,函数false为偶函数.
false,函数false的大致图象如下图所示:
(2)由图象可知,函数false的值域为false,
单调递增区间为false和false,单调递减区间为false和false.
考向三 根据函数的奇偶性求参数的值
1、若函数false是偶函数,则false等于____.
【答案】1
【解析】由于函数false是偶函数,
所以false即false,
所以false恒成立,所以false.
2、已知 f(x)=ax2+bx 是定义在 [a?1,2a] 上的偶函数,那么 a+b 的值是( )
A.?13 B.13C.12 D.?12
【答案】B
【解析】根据偶函数的定义域关于原点对称,,且 f(x) 是定义在 [a?1,2a] 上的偶函数,得 a?1=?2a,解得 a=13,又 f(?x)=f(x),∴b=0,∴a+b=13.,故选 B
3、若函数false在false上是奇函数,则false的解析式为( ).
A.false B.false
C.false D.false
【答案】B
【解析】false函数false在false上是奇函数
false,
即false,false,false
即false
false,false
解得false
则false
故选false
4、已知函数f(x)=false为定义是区间[-2a,3a-1]上的奇函数,则a+b=________.
【答案】2.
【解析】因为函数false为定义是区间[-2a,3a-1]上的奇函数,所以-2a+3a-1=0,所以a=1.
又false,所以b=1.故a+b=2.
考向四 根据奇偶性求函数值或解析式
1、如图,给出奇函数false的局部图象,则false的值为( )
A.false B.2 C.1 D.0
【答案】A
【解析】由图知false,
又false为奇函数,所以false.
故选A.
2、已知函数false为奇函数,若false,则false .
【答案】1
【解析】因为函数y=f(x)为奇函数,所以f(-2)=-f(2),f(-3)=-f(3).所以
f(-2)-f(-3)=-f(2)+f(3)=1
3、已知 f(x) 是定义在 R 上的奇函数,当x≥0 时, f(x)=x2?2x ,则 f(x) 在R 上的表达式为( )
A.f(x)=x(x?2) B.f(x)=x(|x|?1) C.f(x)=|x|(x?2) D.f(x)=x(|x|?2)
【答案】D
【解析】当x<0,?x>0,f(x)=?f(?x)=?x2?2x又当x≥0 时, f(x)=x2?2x综上,f(x)=x(|x|?2)
4、已知定义在 R 上的奇函数 f(x),当 x>0 时,f(x)=x2+|x|?x,那么 x<0 时,f(x)= ________
【答案】?x2
【解析】当 x<0 时,则?x>0将 ?x 代入 f(x) 解析式,得到 f(?x)=x2+|x|+x因为f(x) 是奇函数所以 f(x)=?f(?x)=?x2?|x|?x=?x2
5、已知false是偶函数,false是奇函数,若false,则false的解析式为_______.
【答案】false
考向一 函数奇偶性的判断
1、下列函数中,是奇函数的为(??? ).
A.false B.false C.false D.false
2、判断下列函数的奇偶性:
(1)f(x)=false+false;
(2)f(x)=false
3、判断函数f(x)={x2?2x+5,(x>0)1,(x=0)?x2?2x?5,(x<0)的奇偶性.
4、已知函数 y=f(x)(x≠0) 对于任意的 x,y∈R 且 x,y≠0 都满足 f(xy)=f(x)+f(y).
(1) 求 f(1),f(?1) 的值;
(2) 判断函数 y=f(x)(x≠0) 的奇偶性.
5、函数 f(x),x∈R,若对于任意实数 a,b,都有 f(a+b)=f(a)+f(b),求证:f(x) 为奇函数.
6、判断下列图像中哪个可以表示偶函数
7、函数false的奇偶性为________(填奇函数或偶函数) .
8、已知false,则“false”是“false是偶函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
9、如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是( )
(A)y=x+f(x) (B)y=xf(x)
(C)y=x2+f(x) (D)y=x2f(x)
考向二 奇偶性的性质
1、偶函数false在区间false上的图象如图,则函数false的增区间为______________.
2、已知函数false.
(1)判断false的奇偶性,由此作出false的大致图象;
(2)求false的值域和单调区间.
考向三 根据函数的奇偶性求参数的值
1、若函数false是偶函数,则false等于____.
2、已知 f(x)=ax2+bx 是定义在 [a?1,2a] 上的偶函数,那么 a+b 的值是( )
A.?13 B.13C.12 D.?12
3、若函数false在false上是奇函数,则false的解析式为( ).
A.false B.false
C.false D.false
4、已知函数f(x)=false为定义是区间[-2a,3a-1]上的奇函数,则a+b=________.
考向四 根据奇偶性求函数值或解析式
1、如图,给出奇函数false的局部图象,则false的值为( )
A.false B.2 C.1 D.0
2、已知函数false为奇函数,若false,则false .
3、已知 f(x) 是定义在 R 上的奇函数,当x≥0 时, f(x)=x2?2x ,则 f(x) 在R 上的表达式为( )
A.f(x)=x(x?2) B.f(x)=x(|x|?1) C.f(x)=|x|(x?2) D.f(x)=x(|x|?2)
4、已知定义在 R 上的奇函数 f(x),当 x>0 时,f(x)=x2+|x|?x,那么 x<0 时,f(x)= ________
5、已知false是偶函数,false是奇函数,若false,则false的解析式为_______.
函数的奇偶性
考向一 函数奇偶性的判断
1、下列函数中,是奇函数的为(??? ).
A.false B.false C.false D.false
【答案】A
【解析】对函数false,由于false,因此false,定义域为false,false,因此false为奇函数.
故选A.
2、判断下列函数的奇偶性:
(1)f(x)=false+false;
(2)f(x)=false
【解析】(1)由false得x2=3,解得x=±false,
即函数f(x)的定义域为{-false,false},
从而f(x)=false+false=0.
因此f(-x)=-f(x)且f(-x)=f(x),
∴函数f(x)既是奇函数又是偶函数.
(2)显然函数f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称.
∵当x<0时,-x>0,
则f(-x)=-(-x)2-x=-x2-x=-f(x);
当x>0时,-x<0,
则f(-x)=(-x)2-x=x2-x=-f(x);
综上可知:对于定义域内的任意x,总有f(-x)=-f(x)成立,∴函数f(x)为奇函数.
3、判断函数f(x)={x2?2x+5,(x>0)1,(x=0)?x2?2x?5,(x<0)的奇偶性.
【答案】非奇非偶函数
【解析】1.先判断函数的定义域为R,所以是关于原点对称2.不妨设x>0,则f(x)=x2?2x+5,同时会有?x<0,则有f(?x)=?(?x)2+2x?5=?x2+2x?5=?f(x)3.因为f(0)≠0,所以函数是非奇非偶函数。
4、已知函数 y=f(x)(x≠0) 对于任意的 x,y∈R 且 x,y≠0 都满足 f(xy)=f(x)+f(y).
(1) 求 f(1),f(?1) 的值;
【答案】f(1)=0,f(?1)=0
【解析】令 x=y=1 即可得 f(1),令 x=y=?1 即可得 f(?1)=0.因为对于任意的 x,y∈R 且 x,y≠0 都满足 f(xy)=f(x)+f(y).所以令 x=y=1,得到 f(1)=f(1)+f(1).所以 f(1)=0.令 x=y=?1,得到 f(1)=f(?1)+f(?1).所以 f(?1)=0.
(2) 判断函数 y=f(x)(x≠0) 的奇偶性.
【答案】偶函数
【解析】令 y=?1,得 f(xy)=f(?x)=f(x)+f(?1),由 (1) 可得偶函数.由题意可知,函数 y=f(x) 的定义域为 (?∞,0)∪(0,+∞),关于原点对称.令 y=?1,得 f(xy)=f(?x)=f(x)+f(?1).因为 f(?1)=0.所以 f(?x)=f(x).所以 y=f(x)(x≠0) 为偶函数.
5、函数 f(x),x∈R,若对于任意实数 a,b,都有 f(a+b)=f(a)+f(b),求证:f(x) 为奇函数.
【答案】略
【解析】由于对任意的 x∈(?l,l) 也必有 ?x∈(?l,l),可见,f(?x) 的定义域也是 (?l,l).若设 F(x)=f(x)+f(?x),G(x)=f(x)?f(?x),则 F(x) 与 G(x) 的定义域都是 (?l,l),显然是关于原点对称的区间.而且 F(?x)=f(?x)+f[?(?x)]=f(x)+f(?x)=F(x),故 F(x) 为偶函数. G(?x)=f(?x)?f[?(?x)]=f(?x)?f(x)=?[f(x)?f(?x)]=?G(x),故 G(x) 为奇函数.
6、判断下列图像中哪个可以表示偶函数
【答案】B
【解析】A虽然是轴对称图像,但对称轴不是y轴,所以不是偶函数图像,当然也不是奇函数图像;B关于y轴对称,是偶函数图像;C乍一看上去是中心对称图像,但是要注意,对称性是对图像上任意的一点都满足,x=0和x=3或x=?3时并不满足,所以不是奇函数;D选项最明显,不是奇函数图像也不是偶函数图像;E不关于y轴对称,也不关于原点对称,不是奇函数也不是偶函数;F:首先图像必须为函数图像(回忆函数定义),x=0处对应两个函数值,并不是函数图像,所以F不表示奇偶函数图像.
7、函数false的奇偶性为________(填奇函数或偶函数) .
【答案】奇函数
【解析】
由已知得false 的定义域为false 即false ,则falsefalse 其定义域关于原点对称,false ,所以false 是奇函数.
8、已知false,则“false”是“false是偶函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】C
【解析】
因为false是偶函数,所以false
所以false.所以“false”是“false是偶函数”的充要条件.故选C.
9、如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是( )
(A)y=x+f(x) (B)y=xf(x)
(C)y=x2+f(x) (D)y=x2f(x)
【答案】B
【解析】因为f(x)是奇函数,所以f(-x)=-f(x).
对于A,g(-x)=-x+f(-x)=-x-f(x)=-g(x),所以y=x+f(x)是奇函数.
对于B,g(-x)=-xf(-x)=xf(x)=g(x),所以y=xf(x)是偶函数.
对于C,g(-x)=(-x)2+f(-x)=x2-f(x),所以y=x2+f(x)为非奇非偶函数,
对于D,g(-x)=(-x)2f(-x)=-x2f(x)=-g(x),所以y=x2f(x)是奇函数.故选B.
考向二 奇偶性的性质
1、偶函数false在区间false上的图象如图,则函数false的增区间为______________.
【答案】false和false
【解析】偶函数的图象关于false轴对称,可知函数false的增区间为false和false
2、已知函数false.
(1)判断false的奇偶性,由此作出false的大致图象;
(2)求false的值域和单调区间.
【答案】(1)偶函数,图象见解析;(2)值域为false,增区间为false和false,减区间为false和false.
【解析】(1)对于函数false,false,解得false,
所以,函数false的定义域为false,
又false,所以,函数false为偶函数.
false,函数false的大致图象如下图所示:
(2)由图象可知,函数false的值域为false,
单调递增区间为false和false,单调递减区间为false和false.
考向三 根据函数的奇偶性求参数的值
1、若函数false是偶函数,则false等于____.
【答案】1
【解析】由于函数false是偶函数,
所以false即false,
所以false恒成立,所以false.
2、已知 f(x)=ax2+bx 是定义在 [a?1,2a] 上的偶函数,那么 a+b 的值是( )
A.?13 B.13C.12 D.?12
【答案】B
【解析】根据偶函数的定义域关于原点对称,,且 f(x) 是定义在 [a?1,2a] 上的偶函数,得 a?1=?2a,解得 a=13,又 f(?x)=f(x),∴b=0,∴a+b=13.,故选 B
3、若函数false在false上是奇函数,则false的解析式为( ).
A.false B.false
C.false D.false
【答案】B
【解析】false函数false在false上是奇函数
false,
即false,false,false
即false
false,false
解得false
则false
故选false
4、已知函数f(x)=false为定义是区间[-2a,3a-1]上的奇函数,则a+b=________.
【答案】2.
【解析】因为函数false为定义是区间[-2a,3a-1]上的奇函数,所以-2a+3a-1=0,所以a=1.
又false,所以b=1.故a+b=2.
考向四 根据奇偶性求函数值或解析式
1、如图,给出奇函数false的局部图象,则false的值为( )
A.false B.2 C.1 D.0
【答案】A
【解析】由图知false,
又false为奇函数,所以false.
故选A.
2、已知函数false为奇函数,若false,则false .
【答案】1
【解析】因为函数y=f(x)为奇函数,所以f(-2)=-f(2),f(-3)=-f(3).所以
f(-2)-f(-3)=-f(2)+f(3)=1
3、已知 f(x) 是定义在 R 上的奇函数,当x≥0 时, f(x)=x2?2x ,则 f(x) 在R 上的表达式为( )
A.f(x)=x(x?2) B.f(x)=x(|x|?1) C.f(x)=|x|(x?2) D.f(x)=x(|x|?2)
【答案】D
【解析】当x<0,?x>0,f(x)=?f(?x)=?x2?2x又当x≥0 时, f(x)=x2?2x综上,f(x)=x(|x|?2)
4、已知定义在 R 上的奇函数 f(x),当 x>0 时,f(x)=x2+|x|?x,那么 x<0 时,f(x)= ________
【答案】?x2
【解析】当 x<0 时,则?x>0将 ?x 代入 f(x) 解析式,得到 f(?x)=x2+|x|+x因为f(x) 是奇函数所以 f(x)=?f(?x)=?x2?|x|?x=?x2
5、已知false是偶函数,false是奇函数,若false,则false的解析式为_______.
【答案】false
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
