江苏省宿迁市泗洪县洪翔中学2011-2012学年高二下学期期中考试数学(理)试题
文档属性
| 名称 | 江苏省宿迁市泗洪县洪翔中学2011-2012学年高二下学期期中考试数学(理)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 422.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-04 00:00:00 | ||
图片预览





文档简介
(考试时间为120分钟 分值160分)
一、填空题:本大题共14小题,每小题5分,共70分。不需要写出解答过程,请把答案直接填空在答题卡相应位置上。
1.设集合,则 ▲ .
2.若“”是“”的必要不充分条件,则的最大值为 ▲ .
3.经过点,且与直线垂直的直线方程是 ▲ .
4.若将复数表示为是虚数单位)的形式,则 ▲ .
5.已知实数满足约束条件 则的最大值为 ▲ .
6.在闭区间 [-1,1]上任取两个实数,则它们的和不大于1的概率是 ▲ .
7.设等差数列的公差,,若是与的等比中项,则的值为 ▲ .
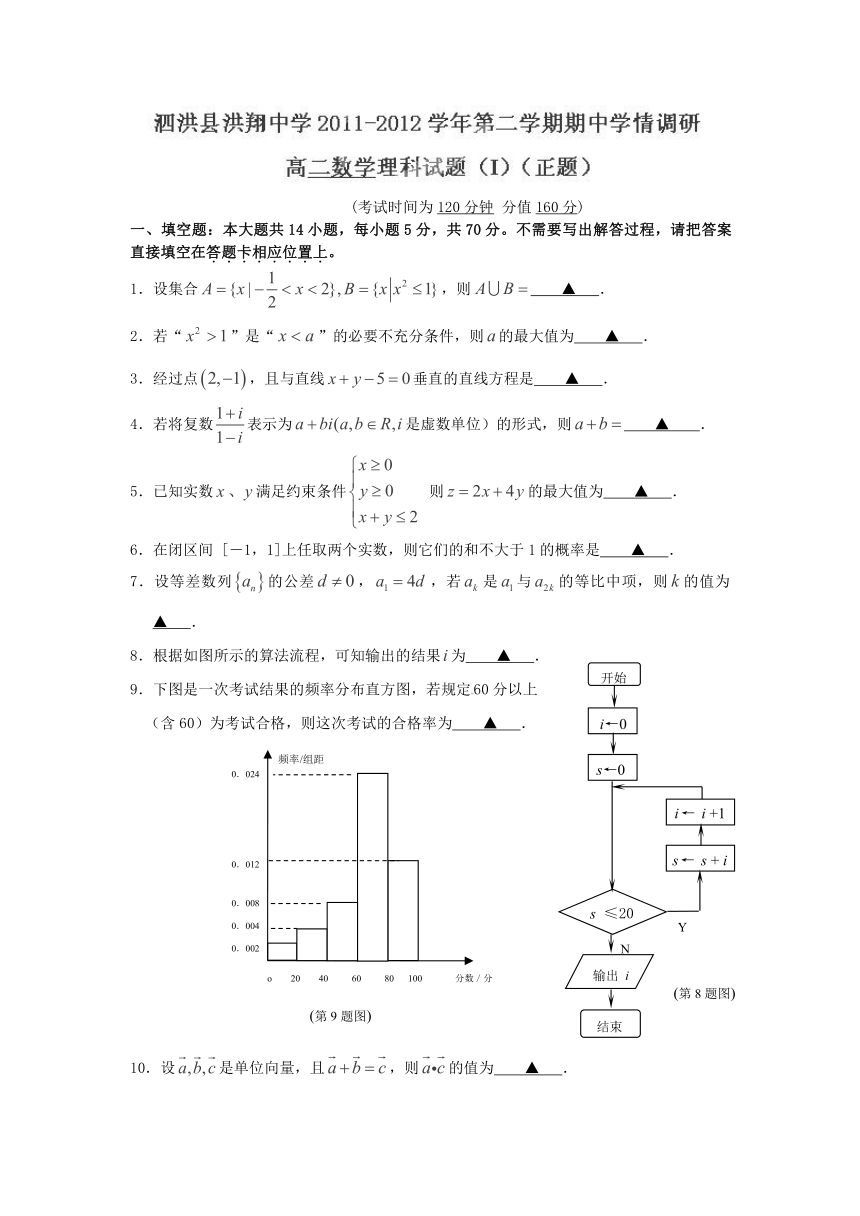
8.根据如图所示的算法流程,可知输出的结果为 ▲ .
9.下图是一次考试结果的频率分布直方图,若规定60分以上
(含60)为考试合格,则这次考试的合格率为 ▲ .
10.设是单位向量,且,则的值为 ▲ .
11.设为正实数,满足,则的最小值是 ▲
12.若不等式对恒成立,则实数的取值范围是 ▲ .
13.五位同学围成一圈依次循环报数,规定,第一位同学首次报出的数为2,第二位同学首次报出的数为3,之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字,则第2013个被报出的数为 ▲ .
14.已知椭圆的左、右焦点分别为,若椭圆上存在点(异于长轴的端点),使得,则该椭圆离心率的取值范围是 ▲ .
二、解答题(本大题共6小题,共90分。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分14分)已知,,.
⑴若∥,求的值;
⑵若,求的值.
16.(本题满分14分)如图,在四棱锥中,四边形为平行四边形,,,为上一点,且平面.
⑴求证:;
⑵如果点为线段的中点,求证:∥平面.
17.(本题满分14分)为赢得2010年上海世博会的制高点,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值(单位:万元, )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
18.(本题满分16分) 已知椭圆:的离心率为,分别为椭圆的左、右焦点,若椭圆的焦距为2.
⑴求椭圆的方程;
⑵设为椭圆上任意一点,以为圆心,为半径作圆,当圆与椭圆的右准线有公共点时,求△面积的最大值.
19.(本题满分16分)已知函数在点处的切线方程为.
⑴求函数的解析式;
⑵若对于区间上任意两个自变量的值都有,求实数的最小值;
⑶若过点可作曲线的三条切线,求实数的取值范围.
20.(本题满分16分)已知数列满足,,n∈N*.
(1)证明:数列是等比数列,并求数列的通项公式;
(2)设,求;
(3)设,求证<.
泗洪县洪翔中学2011-2012学年第二学期期中学情调研
高二数学理科试题(II)(附加题)
(考试时间为30分钟 分值40分)
21.[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内
21B.(选修4—2:矩阵与变换)
二阶矩阵M对应的变换将点与分别变换成点与.
(Ⅰ)求矩阵M的逆矩阵;
(Ⅱ)设直线在变换M作用下得到了直线:,求直线的方程.
21C.(选修4—4:坐标系与参数方程)
在极坐标系中,设圆上的点到直线的距离为,求的最大值.
【必做题】第22题、第23题,每题10分,共计20分. 请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
22.某小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(I)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(II)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数是一个随机变量,求随机变量的分布列及数学期望.
23.如图,在正方体中,点是的中点.
(1) 求与所成的角的余弦值;
(2) 求直线与平面所成的角的余弦值.
命题人:张全军
泗洪县洪翔中学2011-2012学年第二学期期中学情调研
高二数学参考答案(理科)
一、填空题(本大题共14小题,每小题5分,共70分)
1. 2.—1 3. 4.1 5.8 6. 7.3
8.7 9.72% 10. 11.3 12. 13.6 14.
二、解答题(本大题共6小题,共90分。解答应写出文字说明、证明过程或演算步骤)
16.(本题满分14分,第1小题6分,第2小题8分)
证明:⑴因为平面,平面,所以.……………2分
因为,且,平面,
所以平面.……………………………………………………………………4分
因为平面,所以.………………………………………………6分
⑵取中点,连结.
因为平面,平面,所以.
因为,所以为的中点.………………………………………………8分
所以为△的中位线.所以∥,且=.……………10分
因为四边形为平行四边形,所以∥,且.
故∥,且.
因为为中点,所以∥,且.
所以四边形为平行四边形,所以∥.………………………………12分
因为平面,平面,所以∥平面.………………14分
18.(本题满分16分,第1小题6分,第2小题10分)
解:⑴因为,且,所以.……………………………………2分
所以.………………………………………………………………………………4分
所以椭圆的方程为.……………………………………………………6分
⑵设点的坐标为,则.
因为,,所以直线的方程为.………………………………8分
由于圆与有公共点,所以到 的距离小于或等于圆的半径.
因为,所以,………………10分
即 .
又因为,所以.…………………………12分
解得,又,∴.……………………………………14分
当时,,所以 .…………16分
19.(本题满分16分,第1小题 4分,第2小题4分,第3小题8分)
解:⑴.…………………………………………………………1分
根据题意,得即解得……………………3分
所以.………………………………………………………………4分
⑵令,即.得.
1 2
+ +
↗ 极大值 ↘ 极小值 ↗ 2
因为,,
所以当时,,.………………………………6分
则对于区间上任意两个自变量的值,都有
,所以.
所以的最小值为4.……………………………………………………………………8分
⑶因为点不在曲线上,所以可设切点为.
则.
因为,所以切线的斜率为.………………………………9分
则=,………………………………………………………………11分
即.
因为过点可作曲线的三条切线,
所以方程有三个不同的实数解.
所以函数有三个不同的零点.
则.令,则或.
0 2
+ +
↗ 极大值 ↘ 极小值 ↗
则 ,即,解得.…………………………………16分
(注:此题其它解法正确也给分)
21C.(坐标系与参数方程选做题)
解:将极坐标方程转化为普通方程:………………………………(2分)
可化为 ………………………………………(5分)
在上任取一点A,则点A到直线的距离为
,它的最大值为4 ………………(10分)
22.解:(1)记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的,……1分
则其概率为 ………………………………………3分
答:恰好选到1个曾经参加过数学研究性学习活动的同学的概率为……………4分
(2)随机变量
……………………5分
…………………………6分
………………………………7分
∴随机变量的分布列为
2 3 4
P
∴ …………………………10分
Y
i← i +1
输出 i
开始
s← s + i
s ≤20
s←0
i←0
结束
N
(第8题图)
0.024
0.012
0.008
0.004
0.002
频率/组距
o 20 40 60 80 100 分数/分
(第9题图)
一、填空题:本大题共14小题,每小题5分,共70分。不需要写出解答过程,请把答案直接填空在答题卡相应位置上。
1.设集合,则 ▲ .
2.若“”是“”的必要不充分条件,则的最大值为 ▲ .
3.经过点,且与直线垂直的直线方程是 ▲ .
4.若将复数表示为是虚数单位)的形式,则 ▲ .
5.已知实数满足约束条件 则的最大值为 ▲ .
6.在闭区间 [-1,1]上任取两个实数,则它们的和不大于1的概率是 ▲ .
7.设等差数列的公差,,若是与的等比中项,则的值为 ▲ .
8.根据如图所示的算法流程,可知输出的结果为 ▲ .
9.下图是一次考试结果的频率分布直方图,若规定60分以上
(含60)为考试合格,则这次考试的合格率为 ▲ .
10.设是单位向量,且,则的值为 ▲ .
11.设为正实数,满足,则的最小值是 ▲
12.若不等式对恒成立,则实数的取值范围是 ▲ .
13.五位同学围成一圈依次循环报数,规定,第一位同学首次报出的数为2,第二位同学首次报出的数为3,之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字,则第2013个被报出的数为 ▲ .
14.已知椭圆的左、右焦点分别为,若椭圆上存在点(异于长轴的端点),使得,则该椭圆离心率的取值范围是 ▲ .
二、解答题(本大题共6小题,共90分。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分14分)已知,,.
⑴若∥,求的值;
⑵若,求的值.
16.(本题满分14分)如图,在四棱锥中,四边形为平行四边形,,,为上一点,且平面.
⑴求证:;
⑵如果点为线段的中点,求证:∥平面.
17.(本题满分14分)为赢得2010年上海世博会的制高点,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值(单位:万元, )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
18.(本题满分16分) 已知椭圆:的离心率为,分别为椭圆的左、右焦点,若椭圆的焦距为2.
⑴求椭圆的方程;
⑵设为椭圆上任意一点,以为圆心,为半径作圆,当圆与椭圆的右准线有公共点时,求△面积的最大值.
19.(本题满分16分)已知函数在点处的切线方程为.
⑴求函数的解析式;
⑵若对于区间上任意两个自变量的值都有,求实数的最小值;
⑶若过点可作曲线的三条切线,求实数的取值范围.
20.(本题满分16分)已知数列满足,,n∈N*.
(1)证明:数列是等比数列,并求数列的通项公式;
(2)设,求;
(3)设,求证<.
泗洪县洪翔中学2011-2012学年第二学期期中学情调研
高二数学理科试题(II)(附加题)
(考试时间为30分钟 分值40分)
21.[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内
21B.(选修4—2:矩阵与变换)
二阶矩阵M对应的变换将点与分别变换成点与.
(Ⅰ)求矩阵M的逆矩阵;
(Ⅱ)设直线在变换M作用下得到了直线:,求直线的方程.
21C.(选修4—4:坐标系与参数方程)
在极坐标系中,设圆上的点到直线的距离为,求的最大值.
【必做题】第22题、第23题,每题10分,共计20分. 请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
22.某小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(I)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(II)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数是一个随机变量,求随机变量的分布列及数学期望.
23.如图,在正方体中,点是的中点.
(1) 求与所成的角的余弦值;
(2) 求直线与平面所成的角的余弦值.
命题人:张全军
泗洪县洪翔中学2011-2012学年第二学期期中学情调研
高二数学参考答案(理科)
一、填空题(本大题共14小题,每小题5分,共70分)
1. 2.—1 3. 4.1 5.8 6. 7.3
8.7 9.72% 10. 11.3 12. 13.6 14.
二、解答题(本大题共6小题,共90分。解答应写出文字说明、证明过程或演算步骤)
16.(本题满分14分,第1小题6分,第2小题8分)
证明:⑴因为平面,平面,所以.……………2分
因为,且,平面,
所以平面.……………………………………………………………………4分
因为平面,所以.………………………………………………6分
⑵取中点,连结.
因为平面,平面,所以.
因为,所以为的中点.………………………………………………8分
所以为△的中位线.所以∥,且=.……………10分
因为四边形为平行四边形,所以∥,且.
故∥,且.
因为为中点,所以∥,且.
所以四边形为平行四边形,所以∥.………………………………12分
因为平面,平面,所以∥平面.………………14分
18.(本题满分16分,第1小题6分,第2小题10分)
解:⑴因为,且,所以.……………………………………2分
所以.………………………………………………………………………………4分
所以椭圆的方程为.……………………………………………………6分
⑵设点的坐标为,则.
因为,,所以直线的方程为.………………………………8分
由于圆与有公共点,所以到 的距离小于或等于圆的半径.
因为,所以,………………10分
即 .
又因为,所以.…………………………12分
解得,又,∴.……………………………………14分
当时,,所以 .…………16分
19.(本题满分16分,第1小题 4分,第2小题4分,第3小题8分)
解:⑴.…………………………………………………………1分
根据题意,得即解得……………………3分
所以.………………………………………………………………4分
⑵令,即.得.
1 2
+ +
↗ 极大值 ↘ 极小值 ↗ 2
因为,,
所以当时,,.………………………………6分
则对于区间上任意两个自变量的值,都有
,所以.
所以的最小值为4.……………………………………………………………………8分
⑶因为点不在曲线上,所以可设切点为.
则.
因为,所以切线的斜率为.………………………………9分
则=,………………………………………………………………11分
即.
因为过点可作曲线的三条切线,
所以方程有三个不同的实数解.
所以函数有三个不同的零点.
则.令,则或.
0 2
+ +
↗ 极大值 ↘ 极小值 ↗
则 ,即,解得.…………………………………16分
(注:此题其它解法正确也给分)
21C.(坐标系与参数方程选做题)
解:将极坐标方程转化为普通方程:………………………………(2分)
可化为 ………………………………………(5分)
在上任取一点A,则点A到直线的距离为
,它的最大值为4 ………………(10分)
22.解:(1)记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的,……1分
则其概率为 ………………………………………3分
答:恰好选到1个曾经参加过数学研究性学习活动的同学的概率为……………4分
(2)随机变量
……………………5分
…………………………6分
………………………………7分
∴随机变量的分布列为
2 3 4
P
∴ …………………………10分
Y
i← i +1
输出 i
开始
s← s + i
s ≤20
s←0
i←0
结束
N
(第8题图)
0.024
0.012
0.008
0.004
0.002
频率/组距
o 20 40 60 80 100 分数/分
(第9题图)
同课章节目录
