轴对称
图片预览
文档简介
轴对称
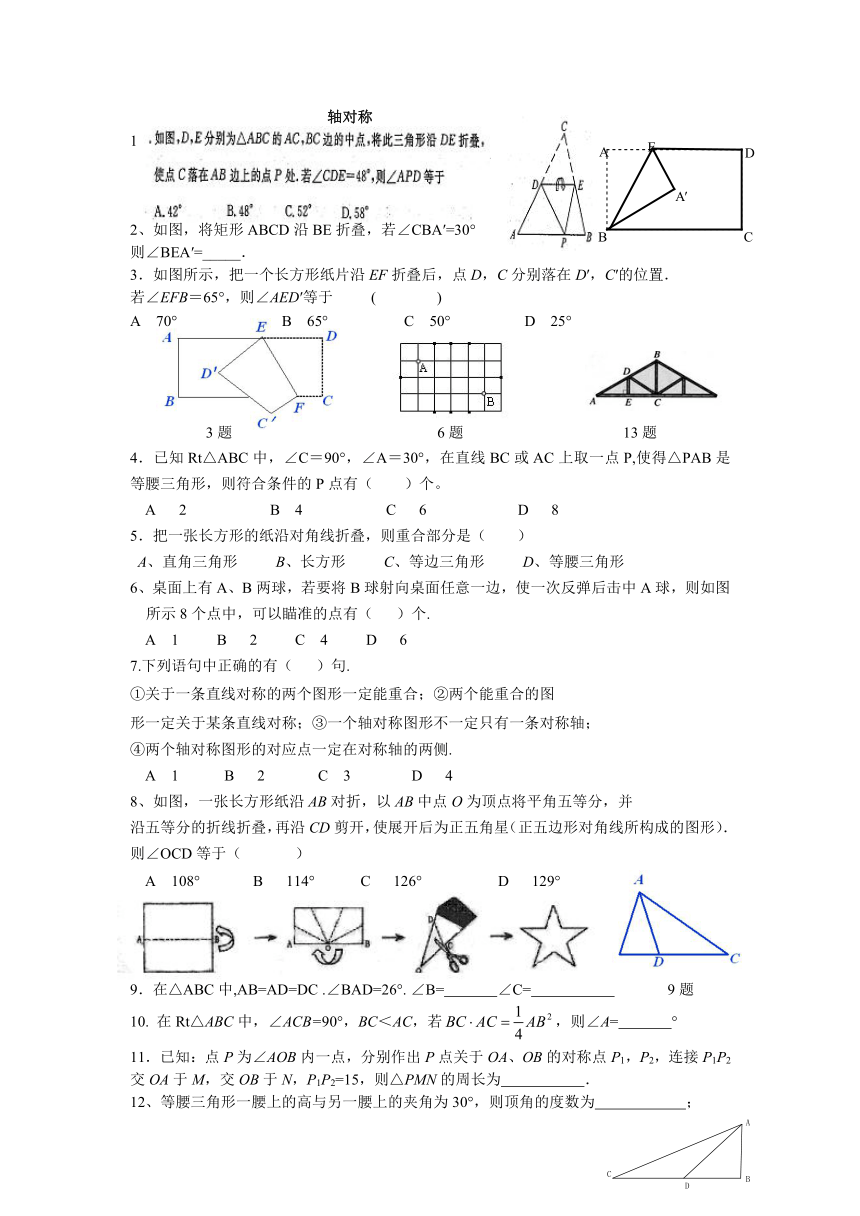
1
2、如图,将矩形ABCD沿BE折叠,若∠CBA′=30°
则∠BEA′=_____.
3.如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.
若∠EFB=65°,则∠AED′等于 ( )
A 70° B 65° C 50° D 25°
3题 6题 13题
4.已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有( )个。
A 2 B 4 C 6 D 8
5.把一张长方形的纸沿对角线折叠,则重合部分是( )
A、直角三角形 B、长方形 C、等边三角形 D、等腰三角形
6、桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( )个.
A 1 B 2 C 4 D 6
7.下列语句中正确的有( )句.
①关于一条直线对称的两个图形一定能重合;②两个能重合的图
形一定关于某条直线对称;③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
A 1 B 2 C 3 D 4
8、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并
沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形).
则∠OCD等于( )
A 108° B 114° C 126° D 129°
9.在△ABC中,AB=AD=DC .∠BAD=26°. ∠B= ∠C= 9题
10. 在Rt△ABC中,∠ACB=90°,BC<AC,若,则∠A= °
11.已知:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
12、等腰三角形一腰上的高与另一腰上的夹角为30°,则顶角的度数为 ;
13、如图:是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE等于 ;
14.如图:在△ABC中,∠B=90°,AB=BD,AD=CD,则∠CAD= 。
15.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的点P有 个,在正方形ABCD外这样的点P有 个
16.P为等边三角形△ABC所在平面内一点,且△PAB、△PBC、△PCA都是等腰三角形,这样的P点有 个。
17.(1)已知中,,,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
(2)已知中,是其最小的内角,过顶点的一条直线把这个三角形分割成了两个等腰三角形,请探求与之间的关系.
18、如图, 等腰直角△ABC,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上。
(1)如图,若点C的坐标是(2,0),点A的坐标是(-2,-2),求B点的坐标;
(2)如图,若y轴恰好平分∠ABC,AC与y轴交与点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由。
(3)如图,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①为定值;②为定值,只有一个结论成立,请你判断正确的结论加以证明并求出定值。
19、如图,已知平面直角坐标系,A、B两点的坐标分别为
A(2,-3),B(4,-1)。
(1)若P(p,0)是x轴上的一个动点,则当p=____时,
△PAB的周长最短;
(2)若C(a,0),D(a+3,0)是x轴上的两个动点,
则当a=____时,四边形ABDC的周长最短
(3)设M,N分别为x轴和y轴上的动点,
请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=____,n=___
(不必写解答过程);若不存在,请说明理由。
A
B
C
A
B
C
A
B
C
1
2、如图,将矩形ABCD沿BE折叠,若∠CBA′=30°
则∠BEA′=_____.
3.如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.
若∠EFB=65°,则∠AED′等于 ( )
A 70° B 65° C 50° D 25°
3题 6题 13题
4.已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有( )个。
A 2 B 4 C 6 D 8
5.把一张长方形的纸沿对角线折叠,则重合部分是( )
A、直角三角形 B、长方形 C、等边三角形 D、等腰三角形
6、桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有( )个.
A 1 B 2 C 4 D 6
7.下列语句中正确的有( )句.
①关于一条直线对称的两个图形一定能重合;②两个能重合的图
形一定关于某条直线对称;③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
A 1 B 2 C 3 D 4
8、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并
沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形).
则∠OCD等于( )
A 108° B 114° C 126° D 129°
9.在△ABC中,AB=AD=DC .∠BAD=26°. ∠B= ∠C= 9题
10. 在Rt△ABC中,∠ACB=90°,BC<AC,若,则∠A= °
11.已知:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
12、等腰三角形一腰上的高与另一腰上的夹角为30°,则顶角的度数为 ;
13、如图:是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE等于 ;
14.如图:在△ABC中,∠B=90°,AB=BD,AD=CD,则∠CAD= 。
15.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的点P有 个,在正方形ABCD外这样的点P有 个
16.P为等边三角形△ABC所在平面内一点,且△PAB、△PBC、△PCA都是等腰三角形,这样的P点有 个。
17.(1)已知中,,,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
(2)已知中,是其最小的内角,过顶点的一条直线把这个三角形分割成了两个等腰三角形,请探求与之间的关系.
18、如图, 等腰直角△ABC,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上。
(1)如图,若点C的坐标是(2,0),点A的坐标是(-2,-2),求B点的坐标;
(2)如图,若y轴恰好平分∠ABC,AC与y轴交与点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由。
(3)如图,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论①为定值;②为定值,只有一个结论成立,请你判断正确的结论加以证明并求出定值。
19、如图,已知平面直角坐标系,A、B两点的坐标分别为
A(2,-3),B(4,-1)。
(1)若P(p,0)是x轴上的一个动点,则当p=____时,
△PAB的周长最短;
(2)若C(a,0),D(a+3,0)是x轴上的两个动点,
则当a=____时,四边形ABDC的周长最短
(3)设M,N分别为x轴和y轴上的动点,
请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=____,n=___
(不必写解答过程);若不存在,请说明理由。
A
B
C
A
B
C
A
B
C
