高一物理生活中的圆周运动ppt课件八
文档属性
| 名称 | 高一物理生活中的圆周运动ppt课件八 |  | |
| 格式 | zip | ||
| 文件大小 | 241.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-05-05 09:42:11 | ||
图片预览





文档简介
(共32张PPT)
生活中的圆周运动
火车车轮的结构特点:
一、铁路的弯道
火车转弯(内外轨道等高)
向左转
N
G
向左转
N
G
F
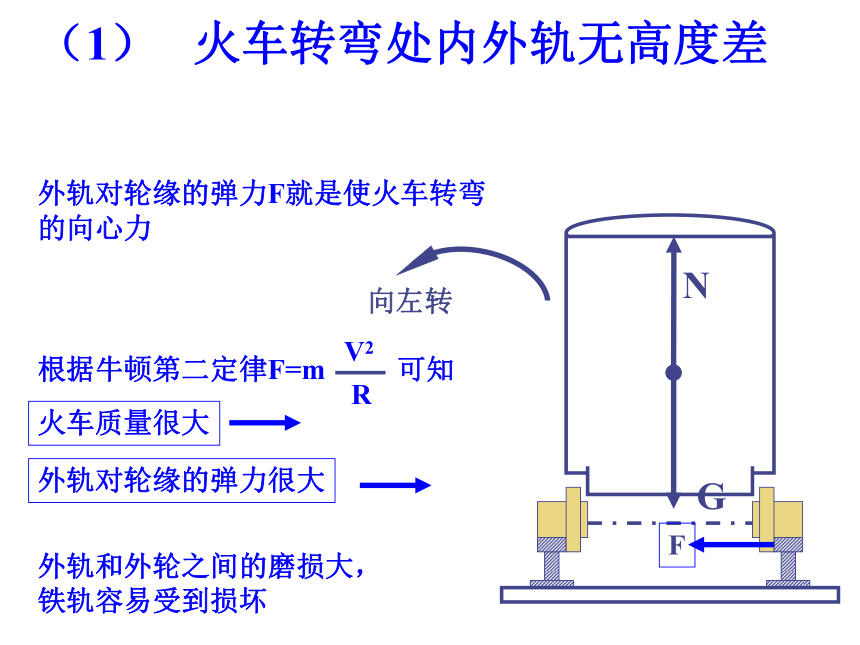
(1) 火车转弯处内外轨无高度差
外轨对轮缘的弹力F就是使火车转弯的向心力
根据牛顿第二定律F=m 可知
R
V2
火车质量很大
外轨对轮缘的弹力很大
外轨和外轮之间的磨损大,
铁轨容易受到损坏
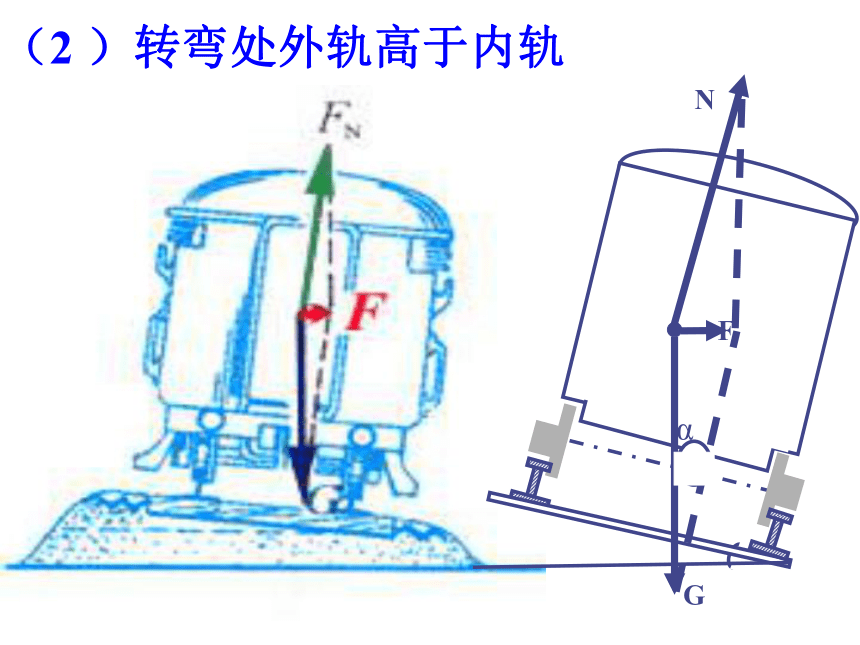
(2 )转弯处外轨高于内轨
根据牛顿第二定律
F=mg tan α=
m
R
V2
V= Rg tanα
V > Rg tanα
V< Rg tanα
外轨对外轮缘有弹力
内轨对内轮缘有弹力
α
N
G
F
α
小结:水平面内的圆周运动,轨迹在水平面内,向心力也一定在水平面内。
向心力是按效果命名的力,任何一个或几个力的合力,只要它的作用效果是使物体产生向心加速度,它就是物体所受的向心力。
在水平铁路转弯处,往往使外轨略高于内轨,这是为了( )
A.减轻火车轮子挤压外轨
B.减轻火车轮子挤压内轨
C.使火车车身倾斜,利用重力 和支持力的合力提供转弯所需向心力
D.限制火车向外脱轨
ACD
思考
在高速公路的拐弯处,路面造得外高内低是什么原因?
(第11题)
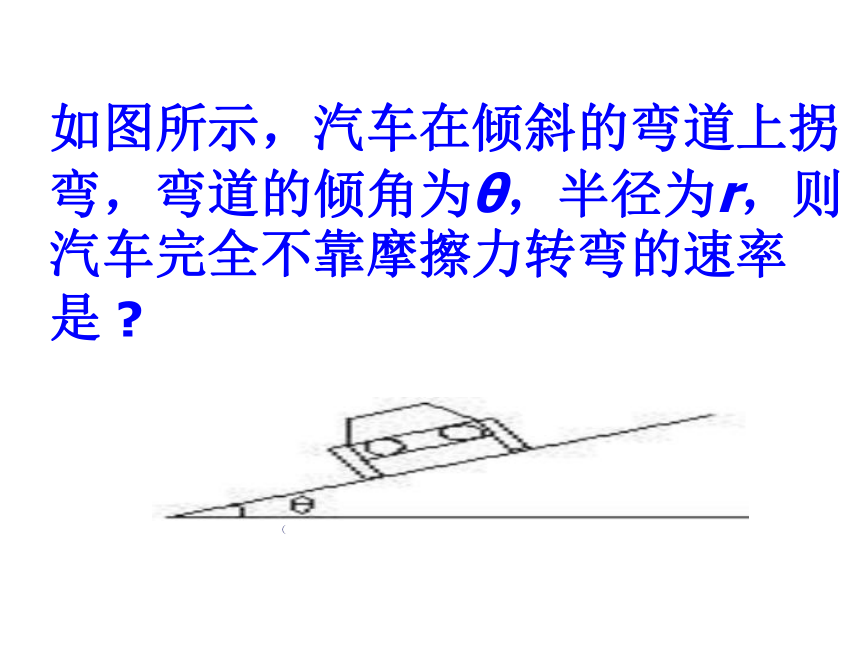
如图所示,汽车在倾斜的弯道上拐弯,弯道的倾角为θ,半径为r,则汽车完全不靠摩擦力转弯的速率是
(
(图)
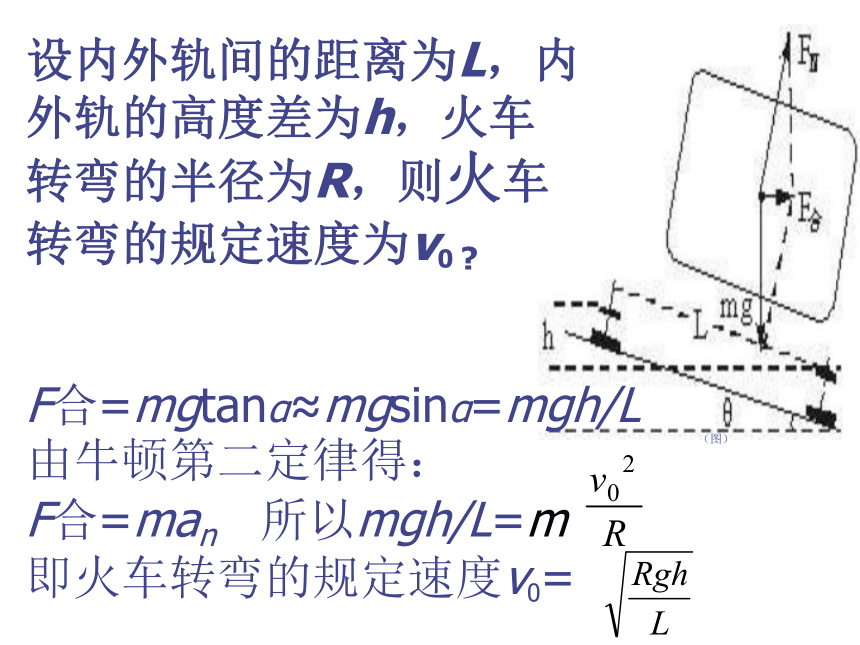
设内外轨间的距离为L,内外轨的高度差为h,火车转弯的半径为R,则火车转弯的规定速度为v0
F合=mgtanα≈mgsinα=mgh/L
由牛顿第二定律得:
F合=man 所以mgh/L=m
即火车转弯的规定速度v0=
V
R
O
G
FN
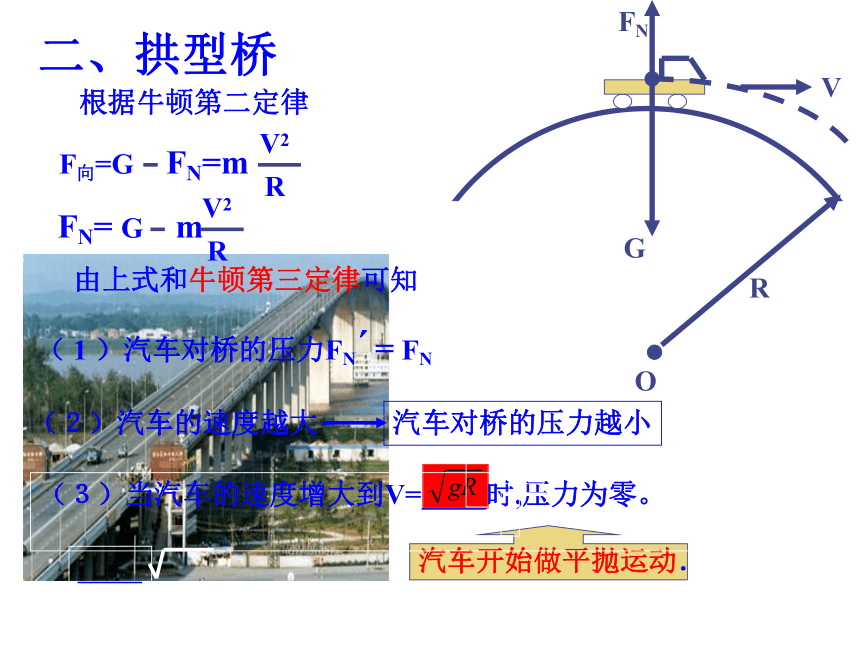
二、拱型桥
F向=G FN=m
R
V2
FN= G m
R
V2
( 1 )汽车对桥的压力FN = FN
(2)汽车的速度越大
汽车对桥的压力越小
由上式和牛顿第三定律可知
根据牛顿第二定律
汽车开始做平抛运动.
(3)当汽车的速度增大到V= 时,压力为零。
V
R
O
质量为m的汽车以速度V通过半径为R的凹型桥。它经桥的最低点时对桥的压力为多大?比汽车的重量大还是小?速度越大压力越大还是越小?
解:
F向=F1 G =m
R
V2
F1 =m +G
R
V2
由上式和牛顿第三定律可知
( 1 )汽车对桥的压力F1 = F1
(2)汽车的速度越大
汽车对桥的压力越大
根据牛顿第二定律
G
F1
思考:汽车不在拱形桥的最高点或最低点时,它的运动能用上面的方法求解吗?
mgcosθ-FN=maN
所以FN=mgcosθ-maN
桥面支持力与夹角θ、车速v都有关。
(
一辆汽车匀速率通过半径为R的圆弧拱形路面,关于汽车的受力情况,下列说法正确的是( )
A.汽车对路面的压力大小不变,总是等于汽车的重力
B.汽车对路面的压力大小不断发生变化,总是小于汽车所受重力
C.汽车的牵引力不发生变化
D.汽车的牵引力逐渐变小
BD
请大家阅读课本58面---思考与讨论 说出你的想法
由 可以解出,当 时座舱对人的支持力F支=0,人处于失重状态
三航天器中的失重现象.
做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动。这种运动叫做离心运动。
一、离心运动
1、离心运动:
2、物体作离心运动的条件:
二、离心运动 应用
1、离心干燥器的金属网笼
利用离心运动把附着在物体上的水分甩掉的装置
解释:
o
F2
F
ν
当网笼转得比较慢时,水滴跟物体的附着力F 足以提供所需的向心力F 使水滴做圆周运动。当网笼转得比较快时,附着力 F 不足以提供所需的向心力 F,于是水滴做离心运动,穿过网孔,飞到网笼外面。
2、洗衣机的脱水筒
3、用离心机把体温计的水银柱甩回玻璃泡内
当离心机转得比较慢时,缩口的阻力 F 足以提供所需的向心力,缩口上方的水银柱做圆周运动。当离心机转得相当快时,阻力 F 不足以提供所需的向心力,水银柱做离心运动而进入玻璃泡内。
4、制作“棉花”糖的原理:
内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁。内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花。
要使原来作圆周运动的物体作离心运动,该怎么办?
?问题一:
A、提高转速,使所需向心力增大到大于物体所受合外力。
B、减小合外力或使其消失
三、离心运动的防止:
1、在水平公路上行驶的汽车转弯时
υ
F < m
υ
r
2
F
汽车
在水平公路上行驶的汽车,转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大,所需向心力F大于最大静摩擦力Fmax,汽车将做离心运动而造成交通事故。因此,在公路弯道处,车辆行驶不允许超过规定的速度。
2、高速转动的砂轮、飞轮等
?问题二:
要防止离心现象发生,该怎么办?
A、减小物体运动的速度,使物体作圆周运动时所需的向心力减小
B、增大合外力,使其达到物体作圆周运动时所需的向心力
C、作匀速圆周运动的物体,它自己会产生一个向心力,维持其作圆周运动
A、作匀速圆周运动的物体,在所受合外力突然消失时,将沿圆周半径方向离开圆心
B、作匀速圆周运动的物体,在所受合外力突然消失时,将沿圆周切线方向离开圆心
D、作离心运动的物体,是因为受到离心力作用的缘故
1、下列说法正确的是 ( )
巩固练习:
B
2、为了防止汽车在水平路面上转弯时出现“打滑”的现象,可以:( )
a、增大汽车转弯时的速度 b、减小汽车转弯时的速度
c、增大汽车与路面间的摩擦 d、减小汽车与路面间的摩擦
A、a、b B、a、c C、b、d D、b、c
3、下列说法中错误的有:( )
A、提高洗衣机脱水筒的转速,可以使衣服甩得更干
B、转动带有雨水的雨伞,水滴将沿圆周半径方向离开圆心
C、为了防止发生事故,高速转动的砂轮、飞轮等不能超过允许的最大转速
D、离心水泵利用了离心运动的原理
D
B
过山车
(1)凸形桥半径为R,汽车在顶端的最大速度是多少?
(2)长为R的轻绳一端系一小球在竖直平面内做圆周运动,它在最高点的最小速度是多少?
(3)如果上题改成长为R的轻杆一端系一小球在竖直平面内做圆周运动,它在最高点的最小速度是多少?当球在最高点速度为 时,求杆对球的作用力,当小球在最高点速度 时,求杆对球的作用力。
巩固应用
例、绳系着装水的桶,在竖直平面内做圆周运动,水的质量m=0.5kg,绳长=40cm.求
(1)桶在最高点水不流出的最小速率?(2)水在最高点速率=3m/s时水对桶底的压力?(g取10m/s2)
A
B
例、质量为1kg的小球沿半径为20cm的圆环在竖直平面内做圆周运动,如图所示,求 (1)小球在圆环的最高点A不掉下来的最小速度是多少?此时小球的向心加速度是多少? (2)若小球仍用以上的速度经过圆环的最高点A,当它运动到圆环的最低点B时,对圆环的压力是多少?此时小球的向心加速度是多少?
巩固应用:
例、长为0.6m的轻杆OA(不计质量),A端插个质量为2.0kg的物体,在竖直平面内绕O点做圆周运动,当球达到最高点的速度分别为3m/s, m/s,2m/s时,求杆对球的作用力各为多少
O
A
巩固应用
例、如图所示,质量为m的小球,用长为L的细绳,悬于光滑斜面上的0点,小球在这个倾角为θ的光滑斜面上做圆周运动,若小球在最高点和最低点的速率分别是vl和v2,则绳在这两个位置时的张力大小分别是多大
巩固应用
生活中的圆周运动
火车车轮的结构特点:
一、铁路的弯道
火车转弯(内外轨道等高)
向左转
N
G
向左转
N
G
F
(1) 火车转弯处内外轨无高度差
外轨对轮缘的弹力F就是使火车转弯的向心力
根据牛顿第二定律F=m 可知
R
V2
火车质量很大
外轨对轮缘的弹力很大
外轨和外轮之间的磨损大,
铁轨容易受到损坏
(2 )转弯处外轨高于内轨
根据牛顿第二定律
F=mg tan α=
m
R
V2
V= Rg tanα
V > Rg tanα
V< Rg tanα
外轨对外轮缘有弹力
内轨对内轮缘有弹力
α
N
G
F
α
小结:水平面内的圆周运动,轨迹在水平面内,向心力也一定在水平面内。
向心力是按效果命名的力,任何一个或几个力的合力,只要它的作用效果是使物体产生向心加速度,它就是物体所受的向心力。
在水平铁路转弯处,往往使外轨略高于内轨,这是为了( )
A.减轻火车轮子挤压外轨
B.减轻火车轮子挤压内轨
C.使火车车身倾斜,利用重力 和支持力的合力提供转弯所需向心力
D.限制火车向外脱轨
ACD
思考
在高速公路的拐弯处,路面造得外高内低是什么原因?
(第11题)
如图所示,汽车在倾斜的弯道上拐弯,弯道的倾角为θ,半径为r,则汽车完全不靠摩擦力转弯的速率是
(
(图)
设内外轨间的距离为L,内外轨的高度差为h,火车转弯的半径为R,则火车转弯的规定速度为v0
F合=mgtanα≈mgsinα=mgh/L
由牛顿第二定律得:
F合=man 所以mgh/L=m
即火车转弯的规定速度v0=
V
R
O
G
FN
二、拱型桥
F向=G FN=m
R
V2
FN= G m
R
V2
( 1 )汽车对桥的压力FN = FN
(2)汽车的速度越大
汽车对桥的压力越小
由上式和牛顿第三定律可知
根据牛顿第二定律
汽车开始做平抛运动.
(3)当汽车的速度增大到V= 时,压力为零。
V
R
O
质量为m的汽车以速度V通过半径为R的凹型桥。它经桥的最低点时对桥的压力为多大?比汽车的重量大还是小?速度越大压力越大还是越小?
解:
F向=F1 G =m
R
V2
F1 =m +G
R
V2
由上式和牛顿第三定律可知
( 1 )汽车对桥的压力F1 = F1
(2)汽车的速度越大
汽车对桥的压力越大
根据牛顿第二定律
G
F1
思考:汽车不在拱形桥的最高点或最低点时,它的运动能用上面的方法求解吗?
mgcosθ-FN=maN
所以FN=mgcosθ-maN
桥面支持力与夹角θ、车速v都有关。
(
一辆汽车匀速率通过半径为R的圆弧拱形路面,关于汽车的受力情况,下列说法正确的是( )
A.汽车对路面的压力大小不变,总是等于汽车的重力
B.汽车对路面的压力大小不断发生变化,总是小于汽车所受重力
C.汽车的牵引力不发生变化
D.汽车的牵引力逐渐变小
BD
请大家阅读课本58面---思考与讨论 说出你的想法
由 可以解出,当 时座舱对人的支持力F支=0,人处于失重状态
三航天器中的失重现象.
做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动。这种运动叫做离心运动。
一、离心运动
1、离心运动:
2、物体作离心运动的条件:
二、离心运动 应用
1、离心干燥器的金属网笼
利用离心运动把附着在物体上的水分甩掉的装置
解释:
o
F
F
ν
当网笼转得比较慢时,水滴跟物体的附着力F 足以提供所需的向心力F 使水滴做圆周运动。当网笼转得比较快时,附着力 F 不足以提供所需的向心力 F,于是水滴做离心运动,穿过网孔,飞到网笼外面。
2、洗衣机的脱水筒
3、用离心机把体温计的水银柱甩回玻璃泡内
当离心机转得比较慢时,缩口的阻力 F 足以提供所需的向心力,缩口上方的水银柱做圆周运动。当离心机转得相当快时,阻力 F 不足以提供所需的向心力,水银柱做离心运动而进入玻璃泡内。
4、制作“棉花”糖的原理:
内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁。内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花。
要使原来作圆周运动的物体作离心运动,该怎么办?
?问题一:
A、提高转速,使所需向心力增大到大于物体所受合外力。
B、减小合外力或使其消失
三、离心运动的防止:
1、在水平公路上行驶的汽车转弯时
υ
F < m
υ
r
2
F
汽车
在水平公路上行驶的汽车,转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大,所需向心力F大于最大静摩擦力Fmax,汽车将做离心运动而造成交通事故。因此,在公路弯道处,车辆行驶不允许超过规定的速度。
2、高速转动的砂轮、飞轮等
?问题二:
要防止离心现象发生,该怎么办?
A、减小物体运动的速度,使物体作圆周运动时所需的向心力减小
B、增大合外力,使其达到物体作圆周运动时所需的向心力
C、作匀速圆周运动的物体,它自己会产生一个向心力,维持其作圆周运动
A、作匀速圆周运动的物体,在所受合外力突然消失时,将沿圆周半径方向离开圆心
B、作匀速圆周运动的物体,在所受合外力突然消失时,将沿圆周切线方向离开圆心
D、作离心运动的物体,是因为受到离心力作用的缘故
1、下列说法正确的是 ( )
巩固练习:
B
2、为了防止汽车在水平路面上转弯时出现“打滑”的现象,可以:( )
a、增大汽车转弯时的速度 b、减小汽车转弯时的速度
c、增大汽车与路面间的摩擦 d、减小汽车与路面间的摩擦
A、a、b B、a、c C、b、d D、b、c
3、下列说法中错误的有:( )
A、提高洗衣机脱水筒的转速,可以使衣服甩得更干
B、转动带有雨水的雨伞,水滴将沿圆周半径方向离开圆心
C、为了防止发生事故,高速转动的砂轮、飞轮等不能超过允许的最大转速
D、离心水泵利用了离心运动的原理
D
B
过山车
(1)凸形桥半径为R,汽车在顶端的最大速度是多少?
(2)长为R的轻绳一端系一小球在竖直平面内做圆周运动,它在最高点的最小速度是多少?
(3)如果上题改成长为R的轻杆一端系一小球在竖直平面内做圆周运动,它在最高点的最小速度是多少?当球在最高点速度为 时,求杆对球的作用力,当小球在最高点速度 时,求杆对球的作用力。
巩固应用
例、绳系着装水的桶,在竖直平面内做圆周运动,水的质量m=0.5kg,绳长=40cm.求
(1)桶在最高点水不流出的最小速率?(2)水在最高点速率=3m/s时水对桶底的压力?(g取10m/s2)
A
B
例、质量为1kg的小球沿半径为20cm的圆环在竖直平面内做圆周运动,如图所示,求 (1)小球在圆环的最高点A不掉下来的最小速度是多少?此时小球的向心加速度是多少? (2)若小球仍用以上的速度经过圆环的最高点A,当它运动到圆环的最低点B时,对圆环的压力是多少?此时小球的向心加速度是多少?
巩固应用:
例、长为0.6m的轻杆OA(不计质量),A端插个质量为2.0kg的物体,在竖直平面内绕O点做圆周运动,当球达到最高点的速度分别为3m/s, m/s,2m/s时,求杆对球的作用力各为多少
O
A
巩固应用
例、如图所示,质量为m的小球,用长为L的细绳,悬于光滑斜面上的0点,小球在这个倾角为θ的光滑斜面上做圆周运动,若小球在最高点和最低点的速率分别是vl和v2,则绳在这两个位置时的张力大小分别是多大
巩固应用
