高一物理向心力课件
图片预览



文档简介
(共18张PPT)
第六章 曲线运动
7、向心力
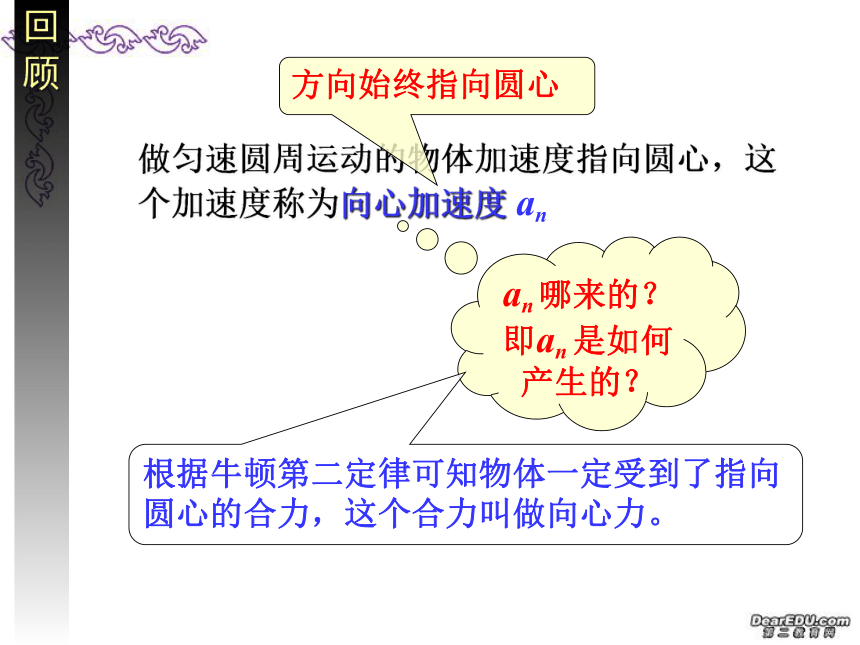
回顾
做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度 an
方向始终指向圆心
an 哪来的?即an 是如何产生的?
根据牛顿第二定律可知物体一定受到了指向圆心的合力,这个合力叫做向心力。
向心力
1、定义:做匀速圆周运动的物体所受到的指向圆心的合外力,叫向心力。
4、效果:只改变v 的方向,不改变v的大小。
3、方向:方向始终与v 垂直,指向圆心。
2、符号:Fn
向心力是不是一种新的性质力?即向心力是不是与重力、弹力、摩擦力一样都是按照某种性质来命名的力?
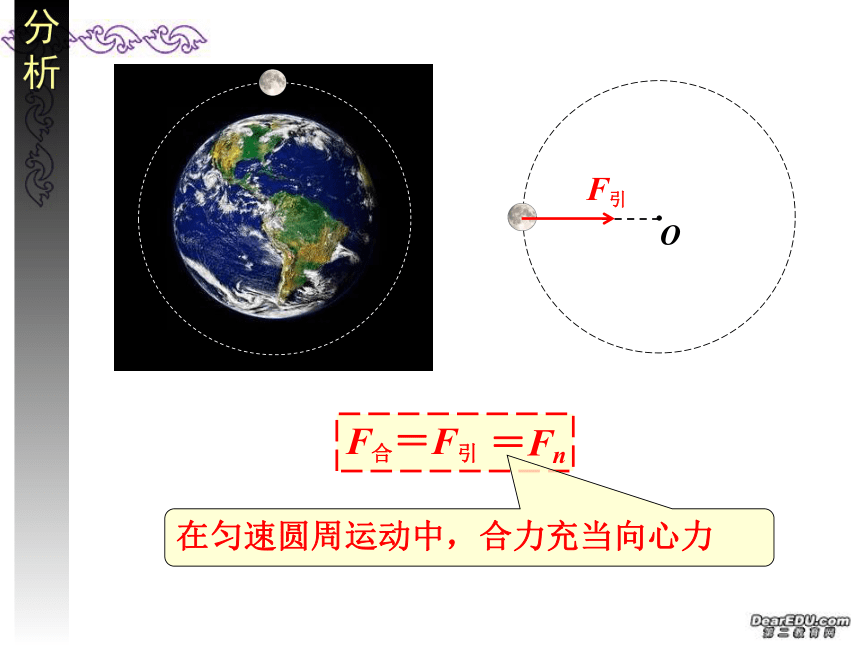
分析
O
F引
F合=F引
=Fn
在匀速圆周运动中,合力充当向心力
O
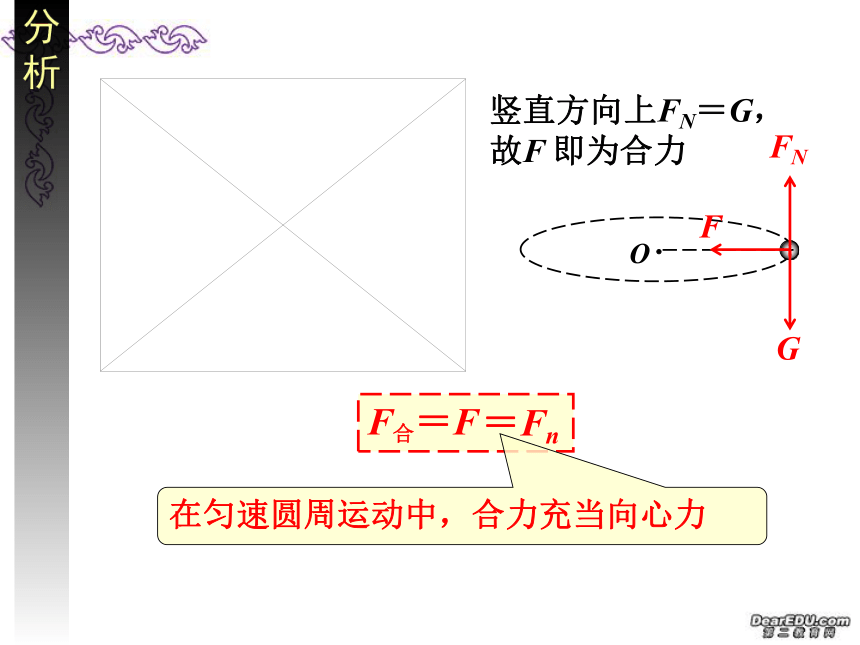
分析
G
FN
F
竖直方向上FN=G,故F 即为合力
F合=F
=Fn
在匀速圆周运动中,合力充当向心力
说明
1、向心力是按照效果命名的力,并不是一种新的性质的力。
F合=Fn
2、向心力的来源:物体所受的合外力提供了物体做匀速圆周运动所需的向心力。(可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力)
在匀速圆周运动中,合力充当向心力
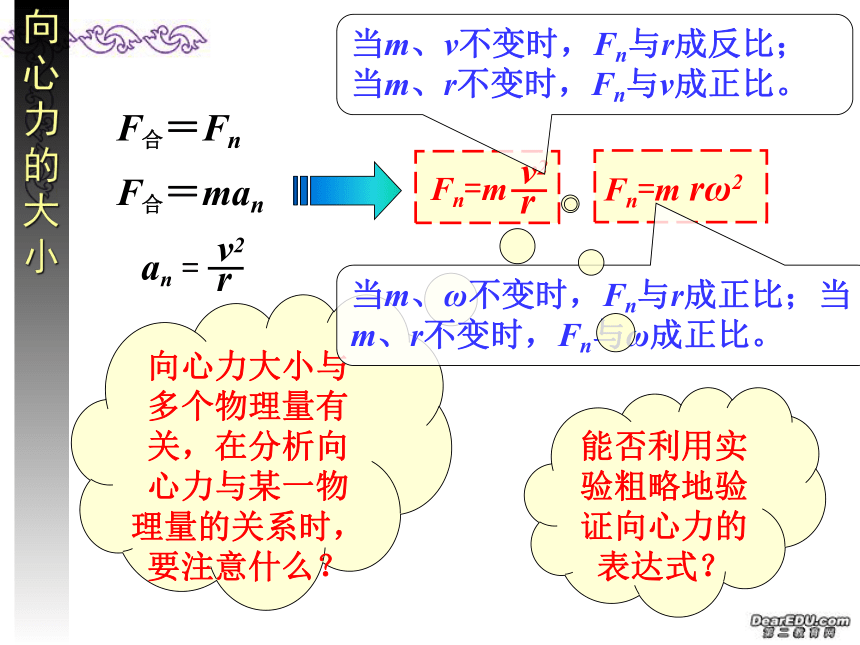
向心力的大小
Fn=m
v2
r
Fn=m rω2
F合=man
向心力大小与多个物理量有关,在分析向心力与某一物理量的关系时,要注意什么?
当m、v不变时,Fn与r成反比;当m、r不变时,Fn与v成正比。
当m、ω不变时,Fn与r成正比;当m、r不变时,Fn与ω成正比。
能否利用实验粗略地验证向心力的表达式?
F合=Fn
an =
v2
r
实验:用圆锥摆粗略验证向心力的表达式
1、实验的基本原理?
从运动的角度求得Fn ;从受力的角度求得F合 ;将Fn 和F合 进行比较
2、实验需要的器材?
钢球、细线、画有同心圆的白纸、天平、秒表、直尺
r
O'
O
θ
l
h
FT
G
F合
3、实验需要测量的数据有哪些?如何测量?
F合=mg tanθ
小球所需向心力
Fn=m
v2
r
m?r?v?θ?
m、r、转n圈数所用时间t、h
注意事项
r
O'
O
θ
l
h
1、h 并不等于纸面距悬点的高度
2、小球与纸面不能接触
3、测 t 时不能太久
4、启动小球时应确保小球做的是匀速圆周运动
实验数据记录
实验次数 运动角度求向心力Fn 受力角度求合力F合
半径r/m 转__圈时间t/s 线速度v/m·s-1 向心力Fn/N 高度h/m 正切值tanθ 合力F合/ N
1
2
3
4
5
小结
3、向心力的大小
2、向心力的作用效果:改变速度的方向
1、向心力的方向:指向圆心
4、向心力的来源
Fn=m
v2
r
Fn=m rω2
Fn =m r
4π2
T 2
在匀速圆周运动中,合力充当向心力
飞机在水平面内盘旋
几种常见的圆周运动
O'
θ
ω
ω
m
O
θ
l
m
竖直方向:FT cosθ=mg
水平方向:F合=mω2l sinθ
竖直方向:F升 cosθ=mg
水平方向:F合=mω2r
O
r
FT
mg
F合
mg
F合
F升
θ
几种常见的圆周运动
θ
O'
O
R
ω
θ
ω
θ
m
m
竖直方向:FN cosθ=mg
水平方向:F合=mω2r
O
r
竖直方向:FN cosθ=mg
水平方向:F合=mω2 R sinθ
mg
FN
F合
mg
FN
F合
O
几种常见的圆周运动
ω
mg
FN
物体相对转盘静止,随盘做匀速圆周运动
r
F静
竖直方向:FN=mg
水平方向:F合=F静=mω2r
F静
v
A
B
F
a
回顾:A、B一起向左加速,分析A的受力情况。
F静
v
谁充当向心力?
静摩擦力指向圆心
O
O
思考
Fn
Ft
F合
v
Fn
Ft
v
F合
速度增大的圆周运动
变速圆周运动
速度减小的圆周运动
匀速圆周运动所受的合力充当向心力,方向始终指向圆心;如果一个沿圆周运动的物体所受的合力不指向圆心,还能做匀速圆周运动吗?
当沿圆周运动的物体所受的合力不指向圆心时,物体做变速圆周运动。
切向力Ft :垂直半径方向的合力
向心力Fn :沿着半径(或指向圆心)的合力
产生切向加速度,改变速度的大小
产生向心加速度,改变速度的方向
分析向心力来源的思路
3、进行受力分析,分析指向圆心方向的合力即向心力
2、确定圆周运动所在的平面,明确圆周运动的轨迹、半径及圆心位置
1、明确研究对象
一般曲线运动
运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般曲线运动。
r1
r2
一般曲线运动各个地方的弯曲程度不一样,如何研究?
把一般曲线分割为许多极短的小段,每一段都可以看作一小段圆弧。这些圆弧的弯曲程度不一样,表明它们具有不同的曲率半径。在分析质点经过曲线上某位置的运动时可以采用圆周运动的分析方法进行处理。
第六章 曲线运动
7、向心力
回顾
做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度 an
方向始终指向圆心
an 哪来的?即an 是如何产生的?
根据牛顿第二定律可知物体一定受到了指向圆心的合力,这个合力叫做向心力。
向心力
1、定义:做匀速圆周运动的物体所受到的指向圆心的合外力,叫向心力。
4、效果:只改变v 的方向,不改变v的大小。
3、方向:方向始终与v 垂直,指向圆心。
2、符号:Fn
向心力是不是一种新的性质力?即向心力是不是与重力、弹力、摩擦力一样都是按照某种性质来命名的力?
分析
O
F引
F合=F引
=Fn
在匀速圆周运动中,合力充当向心力
O
分析
G
FN
F
竖直方向上FN=G,故F 即为合力
F合=F
=Fn
在匀速圆周运动中,合力充当向心力
说明
1、向心力是按照效果命名的力,并不是一种新的性质的力。
F合=Fn
2、向心力的来源:物体所受的合外力提供了物体做匀速圆周运动所需的向心力。(可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力)
在匀速圆周运动中,合力充当向心力
向心力的大小
Fn=m
v2
r
Fn=m rω2
F合=man
向心力大小与多个物理量有关,在分析向心力与某一物理量的关系时,要注意什么?
当m、v不变时,Fn与r成反比;当m、r不变时,Fn与v成正比。
当m、ω不变时,Fn与r成正比;当m、r不变时,Fn与ω成正比。
能否利用实验粗略地验证向心力的表达式?
F合=Fn
an =
v2
r
实验:用圆锥摆粗略验证向心力的表达式
1、实验的基本原理?
从运动的角度求得Fn ;从受力的角度求得F合 ;将Fn 和F合 进行比较
2、实验需要的器材?
钢球、细线、画有同心圆的白纸、天平、秒表、直尺
r
O'
O
θ
l
h
FT
G
F合
3、实验需要测量的数据有哪些?如何测量?
F合=mg tanθ
小球所需向心力
Fn=m
v2
r
m?r?v?θ?
m、r、转n圈数所用时间t、h
注意事项
r
O'
O
θ
l
h
1、h 并不等于纸面距悬点的高度
2、小球与纸面不能接触
3、测 t 时不能太久
4、启动小球时应确保小球做的是匀速圆周运动
实验数据记录
实验次数 运动角度求向心力Fn 受力角度求合力F合
半径r/m 转__圈时间t/s 线速度v/m·s-1 向心力Fn/N 高度h/m 正切值tanθ 合力F合/ N
1
2
3
4
5
小结
3、向心力的大小
2、向心力的作用效果:改变速度的方向
1、向心力的方向:指向圆心
4、向心力的来源
Fn=m
v2
r
Fn=m rω2
Fn =m r
4π2
T 2
在匀速圆周运动中,合力充当向心力
飞机在水平面内盘旋
几种常见的圆周运动
O'
θ
ω
ω
m
O
θ
l
m
竖直方向:FT cosθ=mg
水平方向:F合=mω2l sinθ
竖直方向:F升 cosθ=mg
水平方向:F合=mω2r
O
r
FT
mg
F合
mg
F合
F升
θ
几种常见的圆周运动
θ
O'
O
R
ω
θ
ω
θ
m
m
竖直方向:FN cosθ=mg
水平方向:F合=mω2r
O
r
竖直方向:FN cosθ=mg
水平方向:F合=mω2 R sinθ
mg
FN
F合
mg
FN
F合
O
几种常见的圆周运动
ω
mg
FN
物体相对转盘静止,随盘做匀速圆周运动
r
F静
竖直方向:FN=mg
水平方向:F合=F静=mω2r
F静
v
A
B
F
a
回顾:A、B一起向左加速,分析A的受力情况。
F静
v
谁充当向心力?
静摩擦力指向圆心
O
O
思考
Fn
Ft
F合
v
Fn
Ft
v
F合
速度增大的圆周运动
变速圆周运动
速度减小的圆周运动
匀速圆周运动所受的合力充当向心力,方向始终指向圆心;如果一个沿圆周运动的物体所受的合力不指向圆心,还能做匀速圆周运动吗?
当沿圆周运动的物体所受的合力不指向圆心时,物体做变速圆周运动。
切向力Ft :垂直半径方向的合力
向心力Fn :沿着半径(或指向圆心)的合力
产生切向加速度,改变速度的大小
产生向心加速度,改变速度的方向
分析向心力来源的思路
3、进行受力分析,分析指向圆心方向的合力即向心力
2、确定圆周运动所在的平面,明确圆周运动的轨迹、半径及圆心位置
1、明确研究对象
一般曲线运动
运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般曲线运动。
r1
r2
一般曲线运动各个地方的弯曲程度不一样,如何研究?
把一般曲线分割为许多极短的小段,每一段都可以看作一小段圆弧。这些圆弧的弯曲程度不一样,表明它们具有不同的曲率半径。在分析质点经过曲线上某位置的运动时可以采用圆周运动的分析方法进行处理。
