第二章 轴对称 单元测试题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
《第二章 轴对称》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共24分)
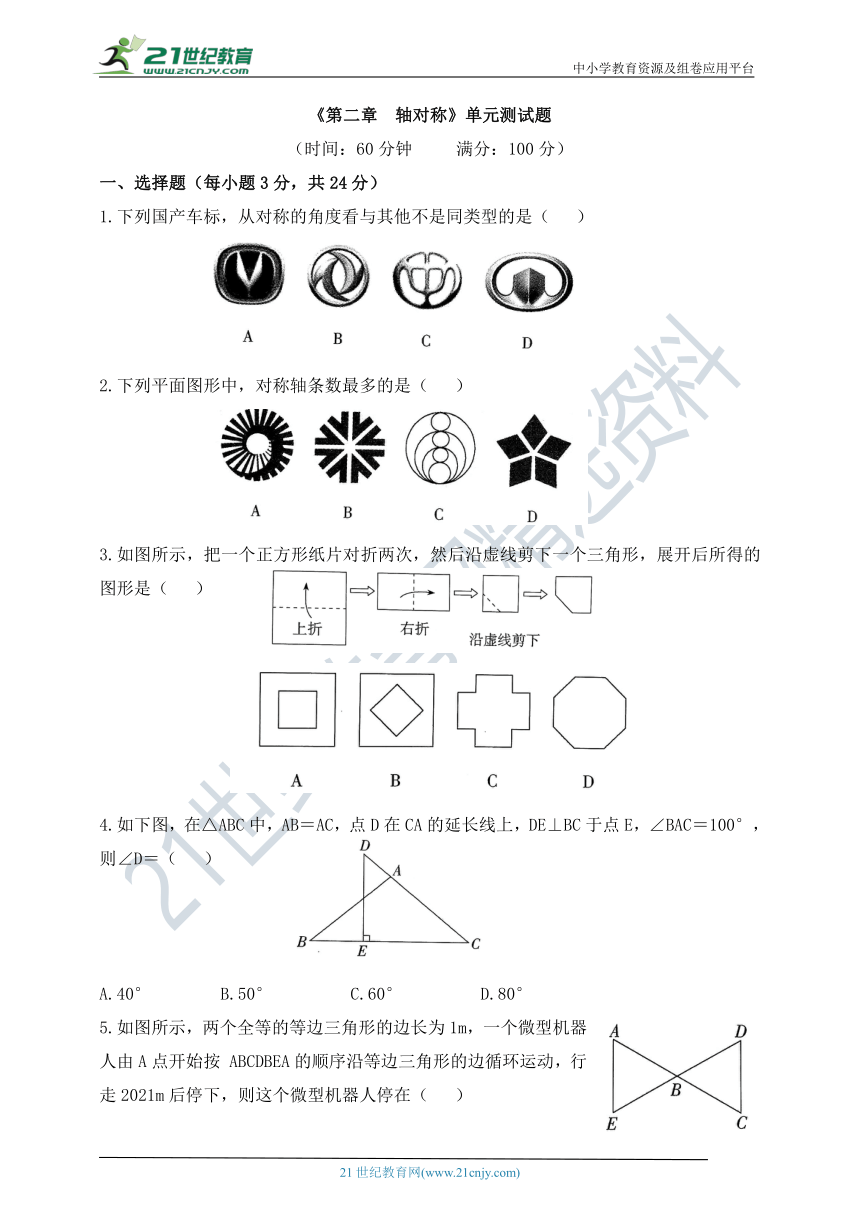
1.下列国产车标,从对称的角度看与其他不是同类型的是( )
2.下列平面图形中,对称轴条数最多的是( )
3.如图所示,把一个正方形纸片对折两次,然后沿虚线剪下一个三角形,展开后所得的图形是( )
4.如下图,在△ABC中,AB=AC,点D在CA的延长线上,DE⊥BC于点E,∠BAC=100°,则∠D=( )
A.40° B.50° C.60° D.80°
5.如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按 ABCDBEA的顺序沿等边三角形的边循环运动,行走2021m后停下,则这个微型机器人停在( )
A.点D处 B.点B处 C.点C处 D.点E处
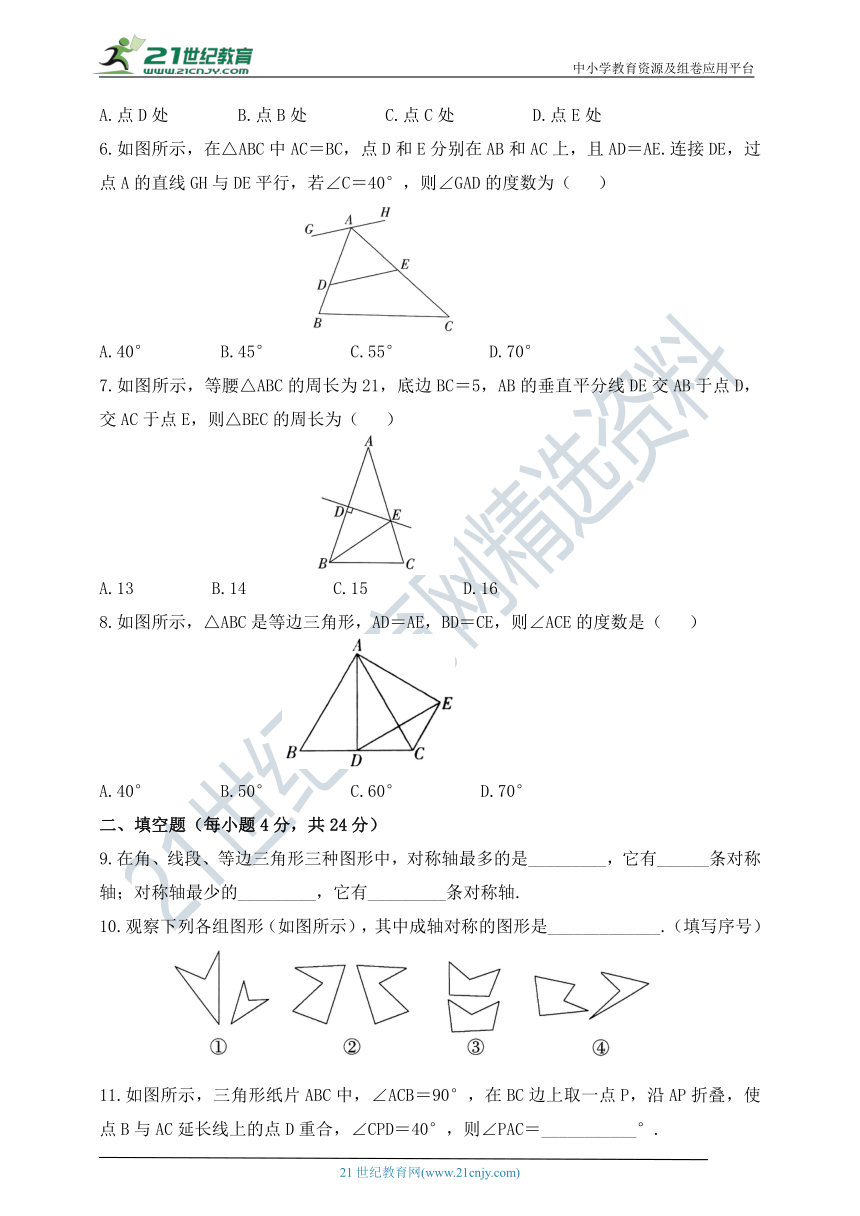
6.如图所示,在△ABC中AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为( )
A.40° B.45° C.55° D.70°
7.如图所示,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
A.13 B.14 C.15 D.16
8.如图所示,△ABC是等边三角形,AD=AE,BD=CE,则∠ACE的度数是( )
A.40° B.50° C.60° D.70°
二、填空题(每小题4分,共24分)
9.在角、线段、等边三角形三种图形中,对称轴最多的是_________,它有______条对称轴;对称轴最少的_________,它有_________条对称轴.
10.观察下列各组图形(如图所示),其中成轴对称的图形是_____________.(填写序号)
11.如图所示,三角形纸片ABC中,∠ACB=90°,在BC边上取一点P,沿AP折叠,使点B与AC延长线上的点D重合,∠CPD=40°,则∠PAC=___________°.
12.如下图,用圆规以直角顶点O为圆心,以适当的长度为半径画一条弧,交直角两边于A,B两点,若再以A为圆心,以OA为半径画弧,与弧AB交于点C,则△AOC的形状为__________.
13.“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动,∠O为∠BDE的三等分角.若∠BDE=75°,则∠CDE的度数是_________.
14.如下图所示,有一艘轮船由东向西航行,在A处测得西偏北15°方向上有一灯塔P,继续航行20海里后到B处,又测得灯塔P在西偏北30°方向上.如果轮船航向不变,则灯塔与轮船之间的最近距离是__________海里.
三、解答题(共52分)
15.(5分)已知:如下图,某镇政府为了方便居民的生活,计划在S区域内修建一个购物广场P,要求到A、B两村子的距离必须相等,到两条公路和的距离也必须相等.请你找出购物广场P应建在哪个位置.(尺规作图,保留作图痕迹,不写作法)
16.(7分)如下图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△ABC关于直线对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)求出△A1B1C1的面积;
(3)在直线上找一点P,使得PA+PB的值最小.
17.(7分)如图所示,四边形ABCD中,AB∥CD,点E为CD上一点,BE、AE分别平
分∠ABC、∠BAD.求证:CD=AD+BC.
18.(7分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=
2:1,BC=7.8cm,求点D到AB的距离.
19.(8分)如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,AC的垂直平分线DE交AB于点D,交AC于点E.
(1)求∠BCD的度数;
(2)若DE=3,求AB的长.
20.(8分)用两个全等的三角形可以拼出各种不同的图形已画出其中一个三角形(如图所示),请你分别?画出另一个与其全等的三角形,使每个图形分别成为不同的轴对称图形,并画出各图形的一条对称轴(所画三角形可与原三角形有重叠的部分,至少设计四种).
21.(10分)已知:如图所示,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
(1)求证:AD=AE;
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
参考答案
一、选择题
1.B 2.B 3.B 4.B 5.D 6.C 7.A 8.C
二、填空题
9.答案 等边三角形;3;角;1 10.答案 ②
11.答案 20 12.答案 等边三角形 13.答案 80° 14.答案 10
三、解答题
15.解析 如图所示点P即为所求.
16.解析
(1)如图所示,△A1B1C1即为所求.
(2)△A1B1C1的面积=.
(3)如图,点P即为所求.
17.证明: ∵AE平分∠DAB,BE平分∠ABC,∴∠DAE=∠BAE,∠ABE=∠EBC,
∵AB∥CD,∴∠BAE=∠DEA,∠ABE=∠BEC,
∴∠DAE=∠DEA,∠EBC=∠BEC,∴AD=DE, BC=CE.
∴CD=DE+CE=AD+BC.
18.解析 过点D作DE⊥AB于E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,∴CD=DE,
又BD: DC=2: 1, BC=7.8 cm,∵DC=7.8÷(2+1)=7.8÷3=2.6cm,
∴DE=DC=2.6cm,∴点D到AB的距离为2.6cm.
19.解析 (1)∵DE垂直平分AC,∴CD=AD,∴∠DCA=∠A=30°,
∵∠ACB=90°,∴∠BCD=∠ACB-∠DCA=90-30°=60°.
(2)∵∠B=90°-∠A=60°,∴∠BCD=∠B,∴BD=CD,
∴BD=CD=AD=AB,
∵DE=3,DE⊥AC,∠A=30°,∴AD=2DE=6,∴AB=2AD=12.
20.解析 如图所示(答案不唯一).
21.解析 (1)证明:如图,∵AB=AC,点D是BC的中点,
∴AD⊥BC,∴∠ADB=90°,∵AE⊥BE,∴∠E=90°=∠ADB,
∵AB平分∠DAE,∴∠1=∠2,
在△ADB和△AEB中,∴△ADB≌△AEB(AAS),∴AD=AE.
(2)△ABC是等边三角形.
理由:∵BE∥AC,∠E=90°,∴∠EAC=∠E=90°,
∵AB=AC,点D是BC的中点,∴∠BAD=∠CAD,又∵AB平分∠DAE,
∴∠EAB=∠BAD=∠DAC=30°,∴∠BAC=∠BAD+∠DAC=60°,
∴△ABC是等边三角形.
_21?????????è?????(www.21cnjy.com)_
《第二章 轴对称》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.下列国产车标,从对称的角度看与其他不是同类型的是( )
2.下列平面图形中,对称轴条数最多的是( )
3.如图所示,把一个正方形纸片对折两次,然后沿虚线剪下一个三角形,展开后所得的图形是( )
4.如下图,在△ABC中,AB=AC,点D在CA的延长线上,DE⊥BC于点E,∠BAC=100°,则∠D=( )
A.40° B.50° C.60° D.80°
5.如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按 ABCDBEA的顺序沿等边三角形的边循环运动,行走2021m后停下,则这个微型机器人停在( )
A.点D处 B.点B处 C.点C处 D.点E处
6.如图所示,在△ABC中AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行,若∠C=40°,则∠GAD的度数为( )
A.40° B.45° C.55° D.70°
7.如图所示,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
A.13 B.14 C.15 D.16
8.如图所示,△ABC是等边三角形,AD=AE,BD=CE,则∠ACE的度数是( )
A.40° B.50° C.60° D.70°
二、填空题(每小题4分,共24分)
9.在角、线段、等边三角形三种图形中,对称轴最多的是_________,它有______条对称轴;对称轴最少的_________,它有_________条对称轴.
10.观察下列各组图形(如图所示),其中成轴对称的图形是_____________.(填写序号)
11.如图所示,三角形纸片ABC中,∠ACB=90°,在BC边上取一点P,沿AP折叠,使点B与AC延长线上的点D重合,∠CPD=40°,则∠PAC=___________°.
12.如下图,用圆规以直角顶点O为圆心,以适当的长度为半径画一条弧,交直角两边于A,B两点,若再以A为圆心,以OA为半径画弧,与弧AB交于点C,则△AOC的形状为__________.
13.“三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动,∠O为∠BDE的三等分角.若∠BDE=75°,则∠CDE的度数是_________.
14.如下图所示,有一艘轮船由东向西航行,在A处测得西偏北15°方向上有一灯塔P,继续航行20海里后到B处,又测得灯塔P在西偏北30°方向上.如果轮船航向不变,则灯塔与轮船之间的最近距离是__________海里.
三、解答题(共52分)
15.(5分)已知:如下图,某镇政府为了方便居民的生活,计划在S区域内修建一个购物广场P,要求到A、B两村子的距离必须相等,到两条公路和的距离也必须相等.请你找出购物广场P应建在哪个位置.(尺规作图,保留作图痕迹,不写作法)
16.(7分)如下图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△ABC关于直线对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)求出△A1B1C1的面积;
(3)在直线上找一点P,使得PA+PB的值最小.
17.(7分)如图所示,四边形ABCD中,AB∥CD,点E为CD上一点,BE、AE分别平
分∠ABC、∠BAD.求证:CD=AD+BC.
18.(7分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=
2:1,BC=7.8cm,求点D到AB的距离.
19.(8分)如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,AC的垂直平分线DE交AB于点D,交AC于点E.
(1)求∠BCD的度数;
(2)若DE=3,求AB的长.
20.(8分)用两个全等的三角形可以拼出各种不同的图形已画出其中一个三角形(如图所示),请你分别?画出另一个与其全等的三角形,使每个图形分别成为不同的轴对称图形,并画出各图形的一条对称轴(所画三角形可与原三角形有重叠的部分,至少设计四种).
21.(10分)已知:如图所示,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
(1)求证:AD=AE;
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
参考答案
一、选择题
1.B 2.B 3.B 4.B 5.D 6.C 7.A 8.C
二、填空题
9.答案 等边三角形;3;角;1 10.答案 ②
11.答案 20 12.答案 等边三角形 13.答案 80° 14.答案 10
三、解答题
15.解析 如图所示点P即为所求.
16.解析
(1)如图所示,△A1B1C1即为所求.
(2)△A1B1C1的面积=.
(3)如图,点P即为所求.
17.证明: ∵AE平分∠DAB,BE平分∠ABC,∴∠DAE=∠BAE,∠ABE=∠EBC,
∵AB∥CD,∴∠BAE=∠DEA,∠ABE=∠BEC,
∴∠DAE=∠DEA,∠EBC=∠BEC,∴AD=DE, BC=CE.
∴CD=DE+CE=AD+BC.
18.解析 过点D作DE⊥AB于E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,∴CD=DE,
又BD: DC=2: 1, BC=7.8 cm,∵DC=7.8÷(2+1)=7.8÷3=2.6cm,
∴DE=DC=2.6cm,∴点D到AB的距离为2.6cm.
19.解析 (1)∵DE垂直平分AC,∴CD=AD,∴∠DCA=∠A=30°,
∵∠ACB=90°,∴∠BCD=∠ACB-∠DCA=90-30°=60°.
(2)∵∠B=90°-∠A=60°,∴∠BCD=∠B,∴BD=CD,
∴BD=CD=AD=AB,
∵DE=3,DE⊥AC,∠A=30°,∴AD=2DE=6,∴AB=2AD=12.
20.解析 如图所示(答案不唯一).
21.解析 (1)证明:如图,∵AB=AC,点D是BC的中点,
∴AD⊥BC,∴∠ADB=90°,∵AE⊥BE,∴∠E=90°=∠ADB,
∵AB平分∠DAE,∴∠1=∠2,
在△ADB和△AEB中,∴△ADB≌△AEB(AAS),∴AD=AE.
(2)△ABC是等边三角形.
理由:∵BE∥AC,∠E=90°,∴∠EAC=∠E=90°,
∵AB=AC,点D是BC的中点,∴∠BAD=∠CAD,又∵AB平分∠DAE,
∴∠EAB=∠BAD=∠DAC=30°,∴∠BAC=∠BAD+∠DAC=60°,
∴△ABC是等边三角形.
_21?????????è?????(www.21cnjy.com)_
