1.2回归分析
图片预览


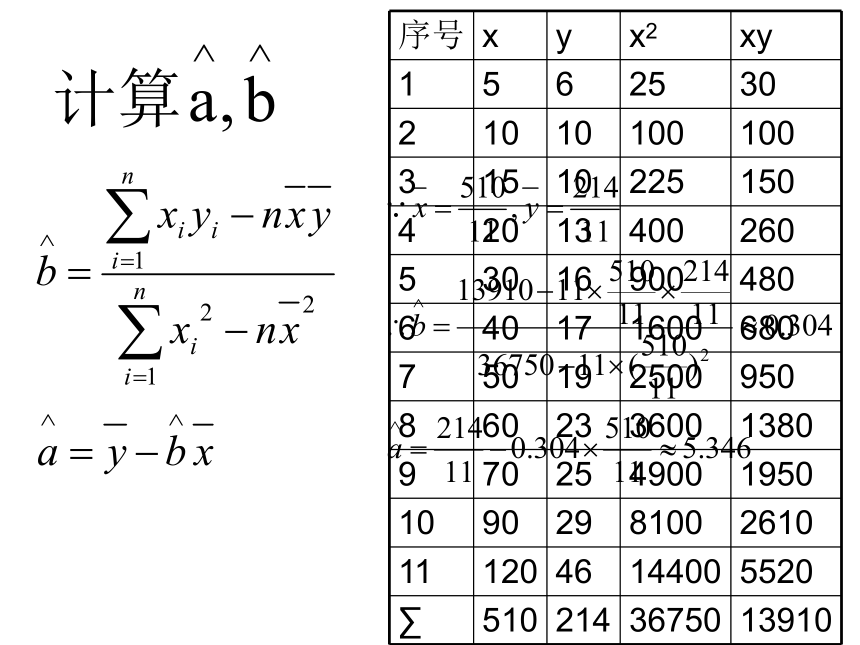



文档简介
(共24张PPT)
1.2回归分析(1)
散点图
两个变量的线性相关
回归系数,回归直线方程
复习回顾
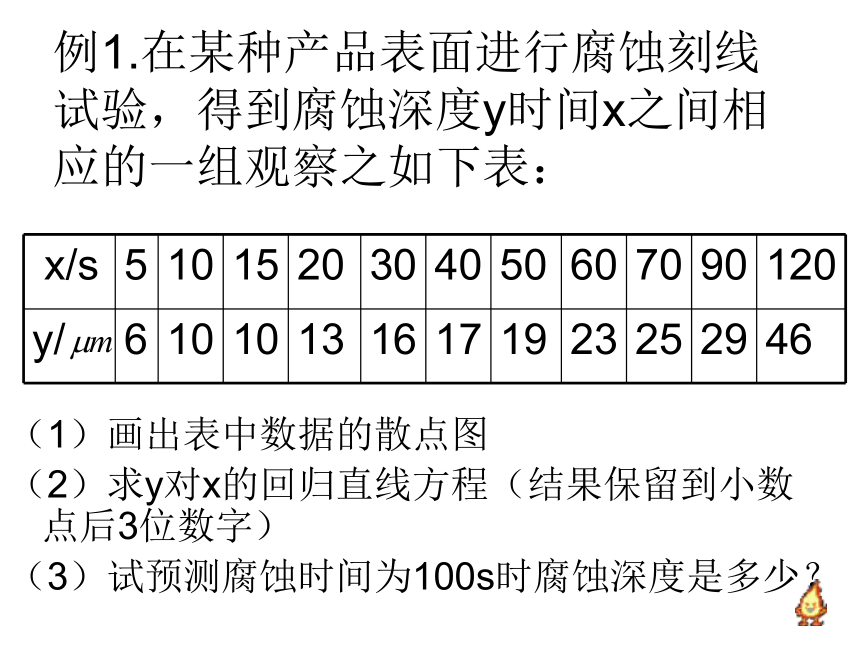
例1.在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y时间x之间相应的一组观察之如下表:
(1)画出表中数据的散点图
(2)求y对x的回归直线方程(结果保留到小数点后3位数字)
(3)试预测腐蚀时间为100s时腐蚀深度是多少?
x/s 5 10 15 20 30 40 50 60 70 90 120
y/ 6 10 10 13 16 17 19 23 25 29 46
1.4
1.6
2.0
1.8
2.25
1.5
2.0
1.75
x/m
y/ms-1
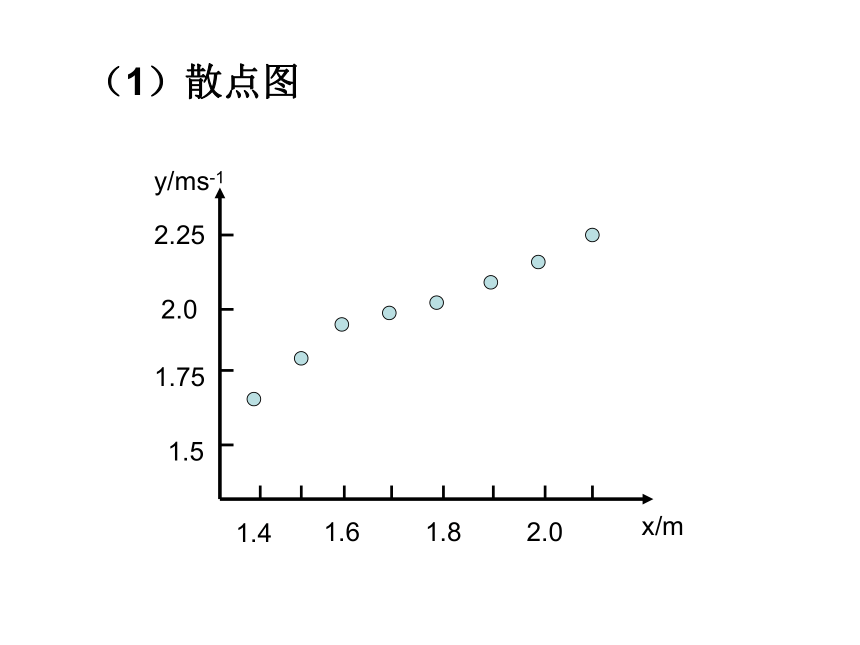
(1)散点图
序号 x y x2 xy
1 5 6 25 30
2 10 10 100 100
3 15 10 225 150
4 20 13 400 260
5 30 16 900 480
6 40 17 1600 680
7 50 19 2500 950
8 60 23 3600 1380
9 70 25 4900 1950
10 90 29 8100 2610
11 120 46 14400 5520
∑ 510 214 36750 13910
例2.为了了解某地母亲身高x与女儿身高y的相关关系,随机测得10对母女身高如下表所示:
母亲身高
x(cm) 159 160 160 163 159 154 159 158 159 157
女儿身高
y(cm) 158 159 160 161 161 155 162 157 162 156
试对x与y进行一元线形回归分析,并预测当母亲身高为161cm时女儿的身高是多少
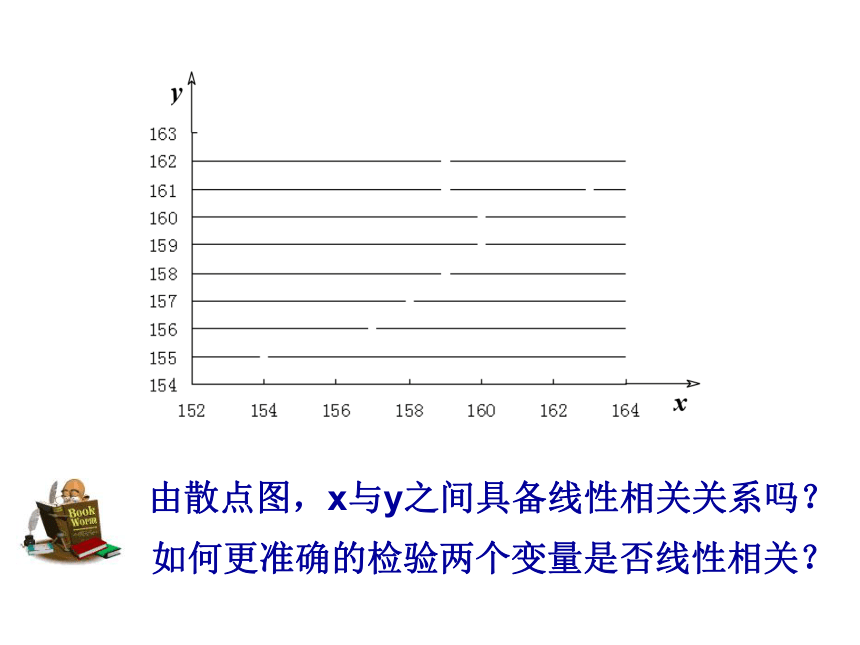
由散点图,x与y之间具备线性相关关系吗?
如何更准确的检验两个变量是否线性相关?
样本相关系数
检验步骤:
先对x与Y作相关性检验
1.作统计假设:x与Y不具有线形相关关系
2.由小概率0.05与n-2=8在附表中查得
点击高考
1.(2011辽宁文14)调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: .由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加______万元.
0.254
点击高考
2.(2011陕西文9 ) 设 ··· ,
是变量x和y的n次方个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论正确的是
A.直线过点
B.x和y的相关系数
为直线l的斜率
C.x和y的相关系数
在0到1之间
D.当n为偶数时,分布在l两侧的样本点的个数一定相同
A
练 习 题
1.设有一个回归方程为 =2-1.5x,则变量x增加一个单位时( ) (A)y平均增加 1.5单位 (B)y平均增加2单位 (C)y平均减少 1.5单位 (D)y平均减少2单位
C
2.回归直线方程 =a+bx必定过点( )
(A)(0,0) (B)( ,0) (C)(0, ) (D)( , )
D
3.下列说法中正确的是( )
A.任何两个变量都具有相关关系
B.人的知识与其年龄具有相关关系
C.散点图中的各点是分散的没有规律
D.根据散点图求得的回归直线方程都是有意义的
B
4.若用水量x与某种产品的产量y的回归直线方程是 =2x+1250,若用水量为 50kg时,预计的某种产品的产量是( ) A.1350 kg B.大于 1350 kg C.小于1350kg D.以上都不对
A
5.若变量y与x之间的相关系数r=-0.9362,查表得到相关系数临界值r0.05=0.8013,则变量y与x之间( ) A.不具有线性相关关系 B.具有线性相关关系 C.它们的线性关系还要进一步确定 D.不确定
B
例3. 某市居民1996~2003年货币收入x与购买商品支出Y的统计资料如下表所示:
年份 1996 1997 1998 1999 2000 2001 2002 2003
货币收入x 36 37 38 40 42 44 47 50
购买商品支出Y 30.0 31.0 32.0 33.2 34.8 36.5 39.0 41.6
试对x与Y的关系进行相关性检验,如x与Y具有线性相关关系,求出Y对x的回归直线方程(结果保留3个有效数字).
单位:亿元
解:(1)画出散点图(单位:亿元)
(2)作统计假设:x与Y不具有线性相关关系.
(3)由小概率事件0.05与n-2=6在附表中查得r0.05=0.707
(4)使用计算器或计算机进行计算得
|r|=0.909>0.707,即|r|>r0.05.
从而有95%的把握认为x与Y具有线性相关关系.
(5)算出线性回归方程中的a和b得
a=0.851,b=0.812.
从而线性回归方程为
1.2回归分析(1)
散点图
两个变量的线性相关
回归系数,回归直线方程
复习回顾
例1.在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y时间x之间相应的一组观察之如下表:
(1)画出表中数据的散点图
(2)求y对x的回归直线方程(结果保留到小数点后3位数字)
(3)试预测腐蚀时间为100s时腐蚀深度是多少?
x/s 5 10 15 20 30 40 50 60 70 90 120
y/ 6 10 10 13 16 17 19 23 25 29 46
1.4
1.6
2.0
1.8
2.25
1.5
2.0
1.75
x/m
y/ms-1
(1)散点图
序号 x y x2 xy
1 5 6 25 30
2 10 10 100 100
3 15 10 225 150
4 20 13 400 260
5 30 16 900 480
6 40 17 1600 680
7 50 19 2500 950
8 60 23 3600 1380
9 70 25 4900 1950
10 90 29 8100 2610
11 120 46 14400 5520
∑ 510 214 36750 13910
例2.为了了解某地母亲身高x与女儿身高y的相关关系,随机测得10对母女身高如下表所示:
母亲身高
x(cm) 159 160 160 163 159 154 159 158 159 157
女儿身高
y(cm) 158 159 160 161 161 155 162 157 162 156
试对x与y进行一元线形回归分析,并预测当母亲身高为161cm时女儿的身高是多少
由散点图,x与y之间具备线性相关关系吗?
如何更准确的检验两个变量是否线性相关?
样本相关系数
检验步骤:
先对x与Y作相关性检验
1.作统计假设:x与Y不具有线形相关关系
2.由小概率0.05与n-2=8在附表中查得
点击高考
1.(2011辽宁文14)调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: .由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加______万元.
0.254
点击高考
2.(2011陕西文9 ) 设 ··· ,
是变量x和y的n次方个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论正确的是
A.直线过点
B.x和y的相关系数
为直线l的斜率
C.x和y的相关系数
在0到1之间
D.当n为偶数时,分布在l两侧的样本点的个数一定相同
A
练 习 题
1.设有一个回归方程为 =2-1.5x,则变量x增加一个单位时( ) (A)y平均增加 1.5单位 (B)y平均增加2单位 (C)y平均减少 1.5单位 (D)y平均减少2单位
C
2.回归直线方程 =a+bx必定过点( )
(A)(0,0) (B)( ,0) (C)(0, ) (D)( , )
D
3.下列说法中正确的是( )
A.任何两个变量都具有相关关系
B.人的知识与其年龄具有相关关系
C.散点图中的各点是分散的没有规律
D.根据散点图求得的回归直线方程都是有意义的
B
4.若用水量x与某种产品的产量y的回归直线方程是 =2x+1250,若用水量为 50kg时,预计的某种产品的产量是( ) A.1350 kg B.大于 1350 kg C.小于1350kg D.以上都不对
A
5.若变量y与x之间的相关系数r=-0.9362,查表得到相关系数临界值r0.05=0.8013,则变量y与x之间( ) A.不具有线性相关关系 B.具有线性相关关系 C.它们的线性关系还要进一步确定 D.不确定
B
例3. 某市居民1996~2003年货币收入x与购买商品支出Y的统计资料如下表所示:
年份 1996 1997 1998 1999 2000 2001 2002 2003
货币收入x 36 37 38 40 42 44 47 50
购买商品支出Y 30.0 31.0 32.0 33.2 34.8 36.5 39.0 41.6
试对x与Y的关系进行相关性检验,如x与Y具有线性相关关系,求出Y对x的回归直线方程(结果保留3个有效数字).
单位:亿元
解:(1)画出散点图(单位:亿元)
(2)作统计假设:x与Y不具有线性相关关系.
(3)由小概率事件0.05与n-2=6在附表中查得r0.05=0.707
(4)使用计算器或计算机进行计算得
|r|=0.909>0.707,即|r|>r0.05.
从而有95%的把握认为x与Y具有线性相关关系.
(5)算出线性回归方程中的a和b得
a=0.851,b=0.812.
从而线性回归方程为
