1.2回归分析2
图片预览



文档简介
(共11张PPT)
1.2回归分析
(2)
样本相关系数
检验步骤:
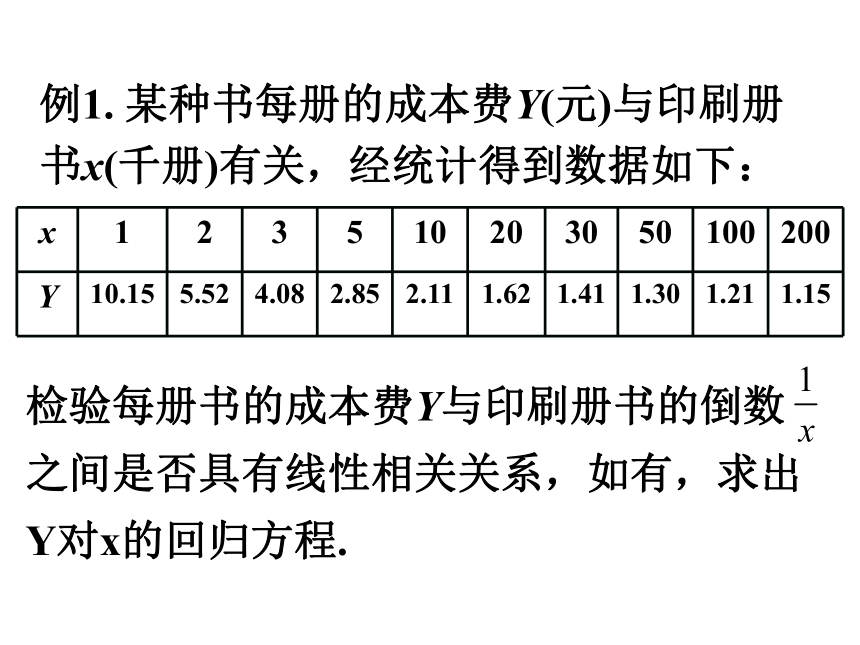
例1. 某种书每册的成本费Y(元)与印刷册书x(千册)有关,经统计得到数据如下:
x 1 2 3 5 10 20 30 50 100 200
Y 10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15
检验每册书的成本费Y与印刷册书的倒数 之间是否具有线性相关关系,如有,求出Y对x的回归方程.
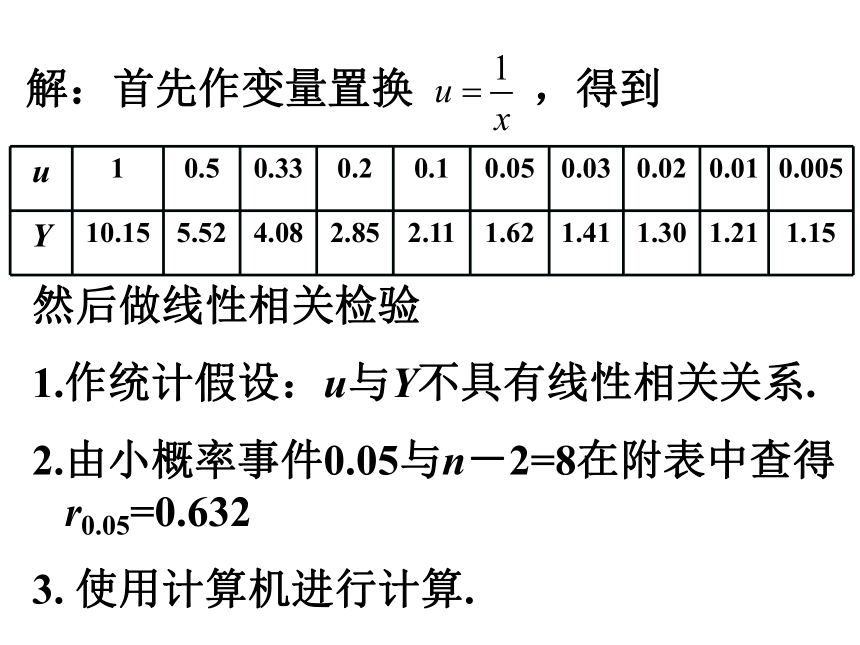
解:首先作变量置换 ,得到
u 1 0.5 0.33 0.2 0.1 0.05 0.03 0.02 0.01 0.005
Y 10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15
然后做线性相关检验
作统计假设:u与Y不具有线性相关关系.
2.由小概率事件0.05与n-2=8在附表中查得r0.05=0.632
3. 使用计算机进行计算.
(4)|r|=0.998
(5)计算可得
把u换回原来的变量,即u=
得到
这就是Y对于x的回归方程.
>0.632,即|r|>y0.05,从而有95%的把握认为u与Y之间具有线性相关关系。求Y对于u的回归直线方程有意义。
点击高考
(2011安徽文20)(本小题满分10分)
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量。
温馨提示:若对数据作适当的预处理,可避免对大数字进行运算。
年份 2002 2004 2006 2008 2010
需求量(万吨) 236 246 257 276 286
年份 2002 2004 2006 2008 2010
需求量(万吨) 236 246 257 276 286
年份—2006 -4 -2 0 2 4
需求量—257 -21 -11 0 19 29
如何对数据进行预处理?
解:(I)由所给数据看出,年需求量与年份之间是近似直线上升,下面来配回归直线方程,为此对数据预处理如下:
年份—2006 -4 -2 0 2 4
需求量—257 -21 -11 0 19 29
对预处理后的数据,容易算得
由上述计算结果,知所求回归直线方程为
(II)利用直线方程,可预测2012年的粮食需求量为
(万吨)≈300(万吨).
1.2回归分析
(2)
样本相关系数
检验步骤:
例1. 某种书每册的成本费Y(元)与印刷册书x(千册)有关,经统计得到数据如下:
x 1 2 3 5 10 20 30 50 100 200
Y 10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15
检验每册书的成本费Y与印刷册书的倒数 之间是否具有线性相关关系,如有,求出Y对x的回归方程.
解:首先作变量置换 ,得到
u 1 0.5 0.33 0.2 0.1 0.05 0.03 0.02 0.01 0.005
Y 10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15
然后做线性相关检验
作统计假设:u与Y不具有线性相关关系.
2.由小概率事件0.05与n-2=8在附表中查得r0.05=0.632
3. 使用计算机进行计算.
(4)|r|=0.998
(5)计算可得
把u换回原来的变量,即u=
得到
这就是Y对于x的回归方程.
>0.632,即|r|>y0.05,从而有95%的把握认为u与Y之间具有线性相关关系。求Y对于u的回归直线方程有意义。
点击高考
(2011安徽文20)(本小题满分10分)
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量。
温馨提示:若对数据作适当的预处理,可避免对大数字进行运算。
年份 2002 2004 2006 2008 2010
需求量(万吨) 236 246 257 276 286
年份 2002 2004 2006 2008 2010
需求量(万吨) 236 246 257 276 286
年份—2006 -4 -2 0 2 4
需求量—257 -21 -11 0 19 29
如何对数据进行预处理?
解:(I)由所给数据看出,年需求量与年份之间是近似直线上升,下面来配回归直线方程,为此对数据预处理如下:
年份—2006 -4 -2 0 2 4
需求量—257 -21 -11 0 19 29
对预处理后的数据,容易算得
由上述计算结果,知所求回归直线方程为
(II)利用直线方程,可预测2012年的粮食需求量为
(万吨)≈300(万吨).
