解直角三角形
图片预览








文档简介
(共22张PPT)
教学目标:
1、继续经历将实际问题化归为直角三角形问题的过程,
探索解直角三角形在解决实际问题中的一些应用;
2、会运用三角函数解决与直角三角形有关的简单实际
问题;
3、进一步体会数形结合和函数思想的运用;
重点:解直角三角形的运用;
难点:例题分析
2.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1. 解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
如图, 在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
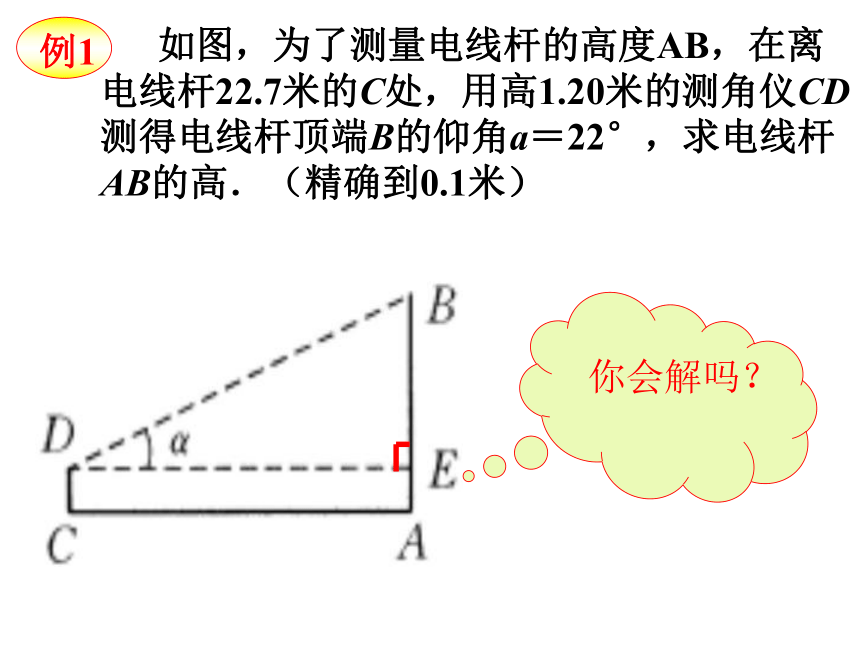
例1
如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
你会解吗?
例1
如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
在Rt△BDE中,
∵ BE=DE×tan a
=AC×tan a
∴AB=BE+AE = AC×tan a +CD =9.17+1.20≈10.4(米)
答: 电线杆的高度约为10.4米.
解:
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角 a=16゜31′,求飞机A到控制点B的距离.(精确到1米)
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.算出旗杆的实际高度.(精确到1米)
例3.某海防哨所O发现在它的北偏西30 ° ,距离哨所500m的A处有一艘船向正东方向航行,经过3分时间后到达哨所东北方向的B处。问船从A处到B处的航速是每时多少km(精确到1km/h)
例4.为知道甲,乙两楼间的距离,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35 ° 12 ′,观测到乙楼底C的俯角为43 ° 24 ′.求这两楼的高度(精确到0.1m)
A
D
C
E
F
B
60°
B
C
A
45°
例1:某海滨浴场的沿岸可以看作直线AC,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的地点C再跳入海中游到B点救助;若每位救生员在岸上 跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒。
D
B
C
A
45°
1. 请问1号救生员的做法是否合理?
2. 若2号救生员从A 跑到D再跳入海中游到B点救助, 请问谁先到达B?
45o
C
B
A
60o
D
45o
C
A
B
如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).
D
60°
45°
A
B
C
B
C
100米
D
B
C
A
45o
45o
C
A
B
60o
D
60o
D
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
翻转
拓展一
B
D
如图,已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 ,由楼顶A望塔底的俯角为30 ,塔高DC为 ( )米
A
C
E
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
旋转
E
拓展二
B
C
D
60
A
E
30
50m
M
45o
A
B
C
45o
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
60o
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
60o
D
60o
D
60o
D
问题1 楼房AB的高度是多少
问题2 楼房CD的高度是多少
拓展三
45o
A
B
C
45o
B
C
A
45o
45o
C
A
B
45o
C
A
B
60o
D
60o
D
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
翻转
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
旋转
E
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
60o
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
60o
D
60o
D
60o
D
30o
C
A
B
45o
D
30o
C
A
B
60o
D
例2、学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?
A
B
4m
600
A
B
D
8m
300
600
C
C
练习
1.如图,某海岛上的观察所A发现海上某船只B并测得其俯角 .已知观察所A的标高(当水位为0m时的高度)为43.74m,当时水位为+2.63m,求观察所A到船只B的水平距离BC(精确到1m).
2.为测量松树AB的高度,一个人站在距松树15米的E
处,测得仰角 ,已知人的高度为1.72米,
求树高(精确到0.01米).
3. 如图所示,已知A、B两点间的距离是160米,
从A点看B点的仰角是11°,AC长为1.5米,求BD的
高及水平距离CD.
1、船有无触礁的危险
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.
要解决这个问题,我们可以将其数学化,如图:
请与同伴交流你是怎么想的 怎么去做
你认为货轮继续向东航行途中会有触礁的危险吗
A
B
C
D
北
东
2、楼梯加长了多少
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
A
B
C
D
┌
3、一渔船在航行中不幸遇险,发出警报后,在遇险地点西南方向12km处,有一只货轮收到警报后立即前往营救,发现这只渔船向南偏东450航行,并以每小时18km的速度向某小岛靠近,如果要在30分钟内把渔船抢救出来,求货轮的航向和速度。
SOS
A
B
C
设计方案测量下面两幢楼的高度。写出需要的数据并画出示意图、给出计算方案。
教学中可让学生尝试分析问题并构造三角形,然后交流不同构造方法的特点和便捷性,鼓励学生学习的积极性,使学习成为主动的富有个性的过程.
教学后应引导学生总结,将实际问题化归为解直角三角形问题,构造适当的直角三角形是关键.航行问题中的三角形往往由方位线和航行路线构成,高度测量问题中的三角形由视线、水平线和铅垂线等构成.方位线、视线可分别由方位角和视角确定,要求学生对方位角、和各种视角(如仰角、俯角、观察角)有准确的理解和想象,并准确画出这些线.
教学目标:
1、继续经历将实际问题化归为直角三角形问题的过程,
探索解直角三角形在解决实际问题中的一些应用;
2、会运用三角函数解决与直角三角形有关的简单实际
问题;
3、进一步体会数形结合和函数思想的运用;
重点:解直角三角形的运用;
难点:例题分析
2.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1. 解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
如图, 在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
例1
如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
你会解吗?
例1
如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
在Rt△BDE中,
∵ BE=DE×tan a
=AC×tan a
∴AB=BE+AE = AC×tan a +CD =9.17+1.20≈10.4(米)
答: 电线杆的高度约为10.4米.
解:
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角 a=16゜31′,求飞机A到控制点B的距离.(精确到1米)
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.算出旗杆的实际高度.(精确到1米)
例3.某海防哨所O发现在它的北偏西30 ° ,距离哨所500m的A处有一艘船向正东方向航行,经过3分时间后到达哨所东北方向的B处。问船从A处到B处的航速是每时多少km(精确到1km/h)
例4.为知道甲,乙两楼间的距离,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35 ° 12 ′,观测到乙楼底C的俯角为43 ° 24 ′.求这两楼的高度(精确到0.1m)
A
D
C
E
F
B
60°
B
C
A
45°
例1:某海滨浴场的沿岸可以看作直线AC,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的地点C再跳入海中游到B点救助;若每位救生员在岸上 跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒。
D
B
C
A
45°
1. 请问1号救生员的做法是否合理?
2. 若2号救生员从A 跑到D再跳入海中游到B点救助, 请问谁先到达B?
45o
C
B
A
60o
D
45o
C
A
B
如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).
D
60°
45°
A
B
C
B
C
100米
D
B
C
A
45o
45o
C
A
B
60o
D
60o
D
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
翻转
拓展一
B
D
如图,已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 ,由楼顶A望塔底的俯角为30 ,塔高DC为 ( )米
A
C
E
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
旋转
E
拓展二
B
C
D
60
A
E
30
50m
M
45o
A
B
C
45o
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
60o
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
60o
D
60o
D
60o
D
问题1 楼房AB的高度是多少
问题2 楼房CD的高度是多少
拓展三
45o
A
B
C
45o
B
C
A
45o
45o
C
A
B
45o
C
A
B
60o
D
60o
D
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
45o
C
A
B
翻转
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
B
C
A
45o
60o
D
旋转
E
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
C
A
B
60o
D
45o
60o
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
60o
D
60o
D
60o
D
30o
C
A
B
45o
D
30o
C
A
B
60o
D
例2、学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?
A
B
4m
600
A
B
D
8m
300
600
C
C
练习
1.如图,某海岛上的观察所A发现海上某船只B并测得其俯角 .已知观察所A的标高(当水位为0m时的高度)为43.74m,当时水位为+2.63m,求观察所A到船只B的水平距离BC(精确到1m).
2.为测量松树AB的高度,一个人站在距松树15米的E
处,测得仰角 ,已知人的高度为1.72米,
求树高(精确到0.01米).
3. 如图所示,已知A、B两点间的距离是160米,
从A点看B点的仰角是11°,AC长为1.5米,求BD的
高及水平距离CD.
1、船有无触礁的危险
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.
要解决这个问题,我们可以将其数学化,如图:
请与同伴交流你是怎么想的 怎么去做
你认为货轮继续向东航行途中会有触礁的危险吗
A
B
C
D
北
东
2、楼梯加长了多少
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
A
B
C
D
┌
3、一渔船在航行中不幸遇险,发出警报后,在遇险地点西南方向12km处,有一只货轮收到警报后立即前往营救,发现这只渔船向南偏东450航行,并以每小时18km的速度向某小岛靠近,如果要在30分钟内把渔船抢救出来,求货轮的航向和速度。
SOS
A
B
C
设计方案测量下面两幢楼的高度。写出需要的数据并画出示意图、给出计算方案。
教学中可让学生尝试分析问题并构造三角形,然后交流不同构造方法的特点和便捷性,鼓励学生学习的积极性,使学习成为主动的富有个性的过程.
教学后应引导学生总结,将实际问题化归为解直角三角形问题,构造适当的直角三角形是关键.航行问题中的三角形往往由方位线和航行路线构成,高度测量问题中的三角形由视线、水平线和铅垂线等构成.方位线、视线可分别由方位角和视角确定,要求学生对方位角、和各种视角(如仰角、俯角、观察角)有准确的理解和想象,并准确画出这些线.
