3.5弧长及扇形的面积(1) 8.17

(共15张PPT)
教学目标：
1、复习圆周长公式；
2、理解弧长公式．
3、通过弧长公式的推导，培养学生抽象、理解、概括、归纳能力；
4、通过“弯道”问题的解决，培养学生从实际问题中抽象出数学模型的能力，综合运用所学知识分析问题和解决问题的能力．
教学重点：
弧长公式．
教学难点：
正确理解弧长公式．
开启 智慧
西气东输工程全长四千多千米,其中有成千上万个圆弧形弯管.制作弯管时，需要按中心计算“展直长度”再下件，你知道怎么样计算这些弯管的长度吗？
o
p
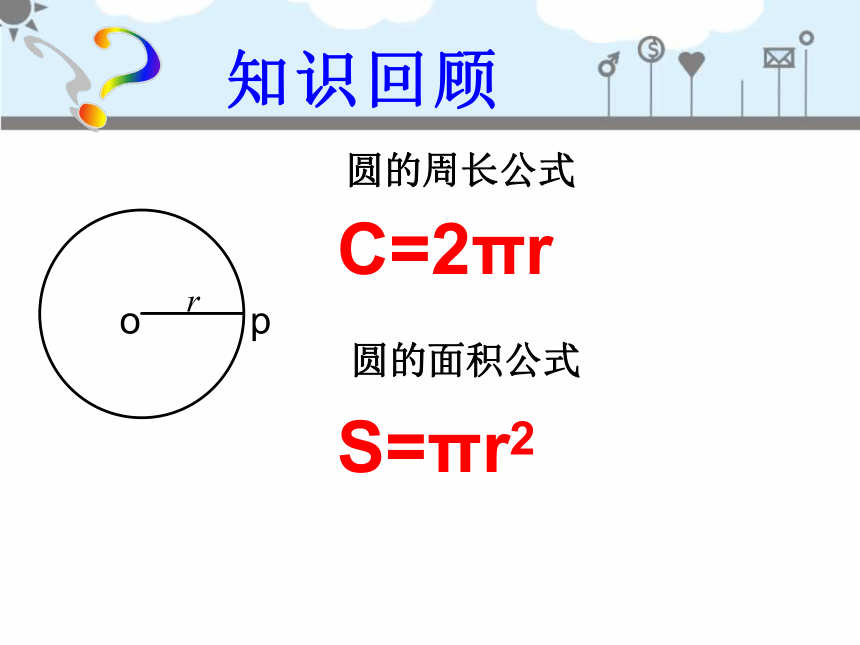
圆的周长公式
圆的面积公式
C=2πr
S=πr2
问题探究
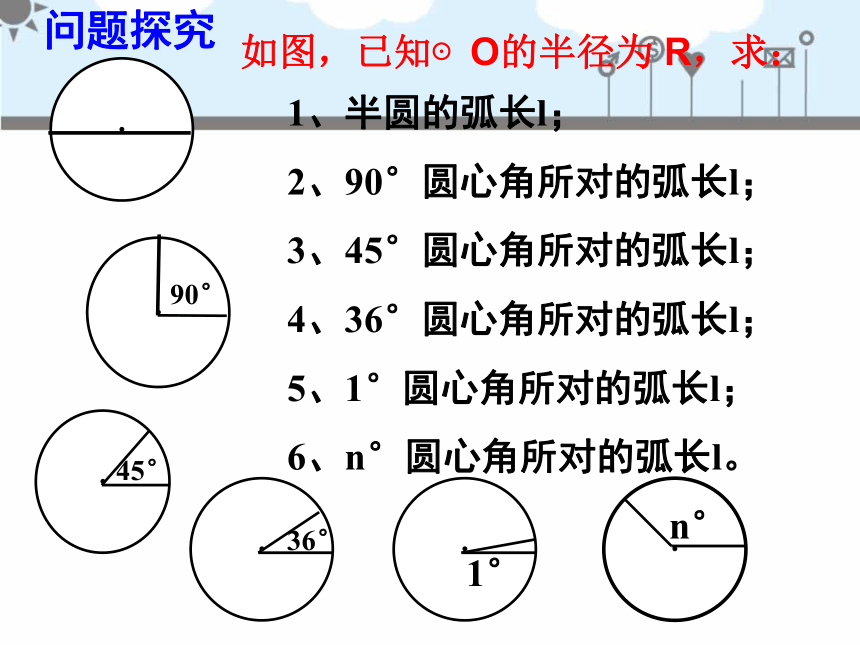
如图，已知⊙O的半径为 R，求：
·
1、半圆的弧长l；
2、90°圆心角所对的弧长l；
3、45°圆心角所对的弧长l；
4、36°圆心角所对的弧长l；
5、1°圆心角所对的弧长l；
6、n°圆心角所对的弧长l。
·
·
·
·
·
90°
45°　　
1°　　
36°　　
n°　　
从上述的练习我们得到怎么样的结论：
在半径为r的圆中，n°的圆心角所对的弧长的计算公式为：
在应用弧长公式l 进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位 的；也可以理解为n和180中的度约去！
注意：
180
R
n
p
=
l
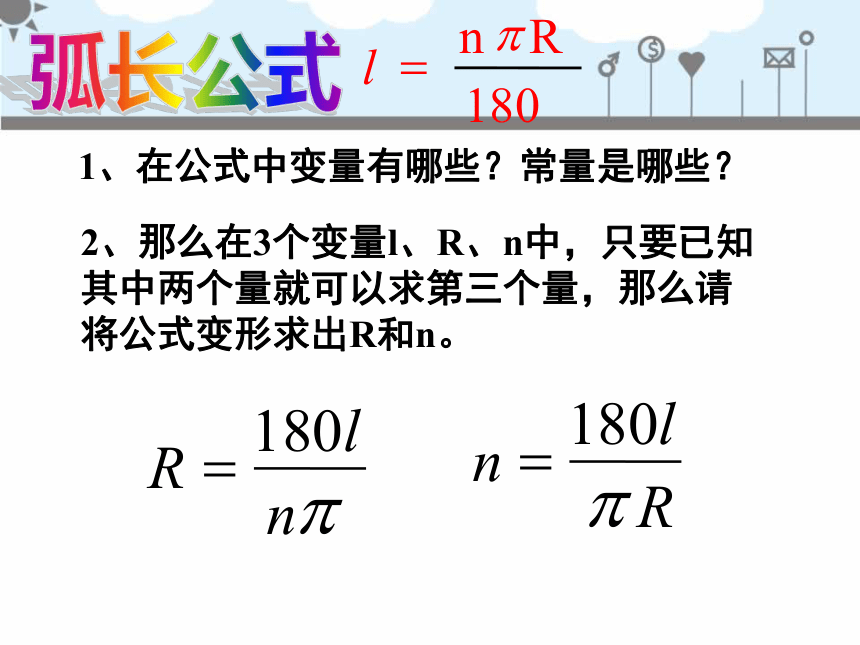
1、在公式中变量有哪些？常量是哪些？
2、那么在3个变量l、R、n中，只要已知其中两个量就可以求第三个量，那么请将公式变形求出R和n。
R
l
n
p
=
180
p
=
n
l
R
180
2.半径为5㎝的圆弧长为5㎝，求这条弧所对的圆心角的度数（精确到0.1°）。
练习：书本P82课内练习
1.直径为100㎝的圆弧的度数20°30′，
　求这条弧长（结果保留３个有效数字）。
4.已知弧长为40 ㎝ ，弧的半径为20㎝ ，求弧的度数。
3.已知圆弧的度数为60°，弧长为6.28㎝ 。求圆的半径。（ 取3.14）
例1 一段圆弧的公路弯道,圆弧的半径是2km,一辆汽车以每小时60km的速度通过弯道,需20秒.求弯道所对的圆心角的度数。(精确到0.1度)
例2 如图，BM是⊙O的直径，四边形ABMN是矩形，D是⊙O上的点，DC⊥AN，与AN交于点C，已知AC＝15，⊙O的半径为Ｒ＝30，
O
B
M
A
N
D
C
求BD的长
⌒
E
辨一辨：下列各命题是真命题还是假命题.
1、度数相等的弧是等弧;
2、长度相等的弧是等弧;
4、在同圆或等圆中,长度相等的弧是等弧;
3、在同圆或等圆中,度数相等的弧是等弧;
A
C
B
A′
C′
课后拓展：如图，把Rt△ABC的斜边放在直线 上，按顺时针方向转动一次,使它转到 的位置。若BC=1,∠A=300。求点A运动到A′位置时，点A经过的路线长。
2. 弧长公式：
l弧＝ C圆
360
n
1. 弧长与哪些因素有关？
（1）与圆心角的大小有关
（2）与半径的长短有关
3. 弧长单位：
弧长单位没有平方的
　１．由于生产、生活实际中常遇到有关弧的长度计算，学过圆的有关性质和小学学过圆周长的基础，研究弧长公式已呈水到渠成之势，所以本节课以推导弧长公式为重点并应用弧长公式解决某些简单的实际问题，在计算过程中常出现由于对“n”理解上的错误而影响计算结果的正确
清楚n°圆心角所对弧长是1°弧长的n倍．
　　２．注意安排不同层次的同学回答不同的问题．