河南省商周联盟2020-2021学年高二下学期期末联考数学文科试题 Word版含答案
文档属性
| 名称 | 河南省商周联盟2020-2021学年高二下学期期末联考数学文科试题 Word版含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 858.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 00:00:00 | ||
图片预览




文档简介
商周联盟2020-2021学年高二下学期期末联考
数学试卷(文科)
一、选择题
1.若复数false满足false(false为虚数单位),则false( ).
A.false B.false C.false D.false
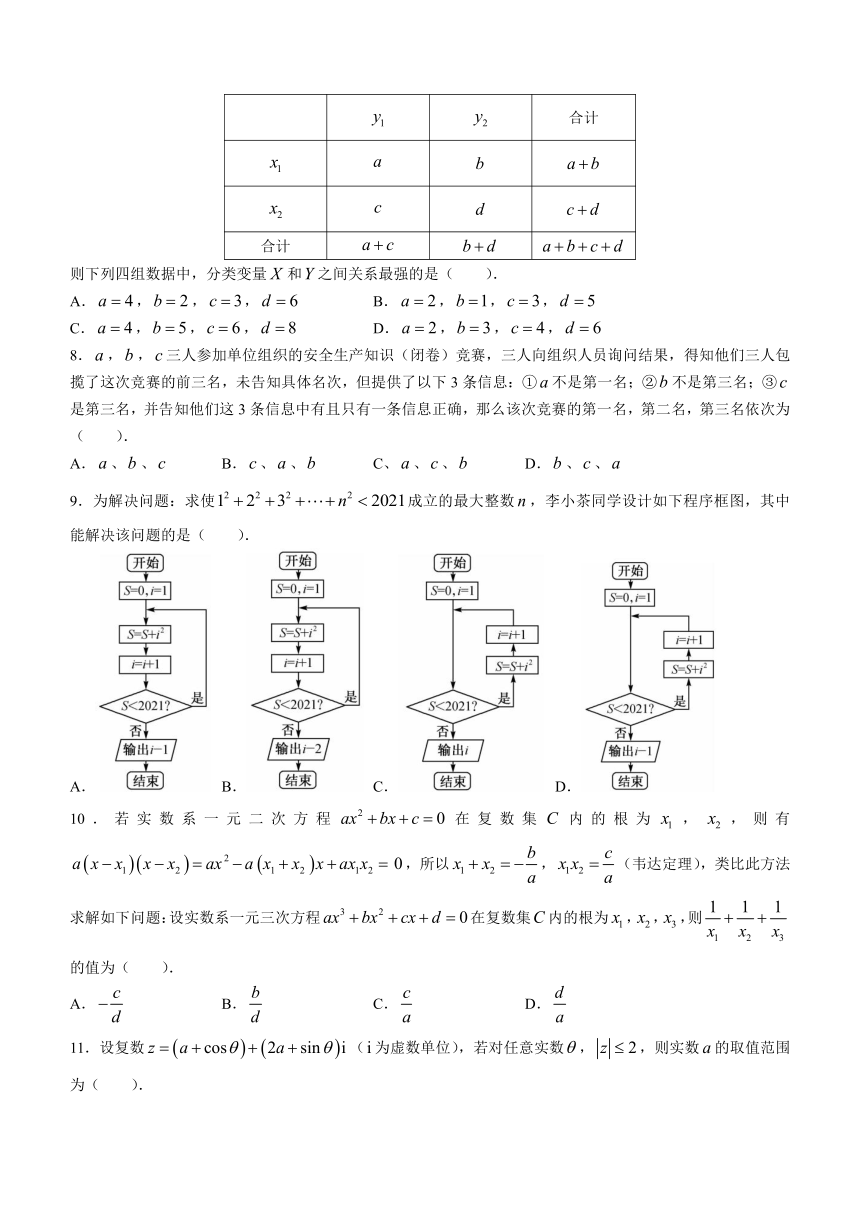
2.如图是某公司的组织结构图,则销售部的直接上位领导是( ).
A.董事会 B.总经理 C.副总经理一 D.副总经理二
3.下列三段话,按演绎推理的三段论模式,排列顺序正确的是( ).
①false,false是两个实数;②任意两个实数之间能比较大小;③false,false之间能比较大小
A.①②③ B.②①③ C.③②① D.②③①
4.某产品的宣传费用false(单位:万元)与销售额false(单位:万元)的统计数据如表所示:
false
4
5
6
7
8
false
60
80
90
100
120
根据上表可得回归直线方程false,则宣传费用为9万元时,销售额约为( ).
A.123万元 B.128万元 C.132万元 D.138万元
5.用反证法证明问题“false,false,false,若false,则false,false,false中至少有一个正数”时,假设为( ).
A.false,false,false均为负数 B.false,false,false中至多一个是正数
C.false,false,false均为正数 D.false,false,false中没有正数
6.已知复数false,false,则下列结论:①若false,则false;②若false,则false;③false;④false;⑤false正确的个数为( ).
A.1 B.2 C.3 D.4
7.两个分类变量false和false,它们的取值分别为false和false,其样本频数列联表如下表所示:
false
false
合计
false
false
false
false
false
false
false
false
合计
false
false
false
则下列四组数据中,分类变量false和false之间关系最强的是( ).
A.false,false,false,false B.false,false,false,false
C.false,false,false,false D.false,false,false,false
8.false,false,false三人参加单位组织的安全生产知识(闭卷)竞赛,三人向组织人员询问结果,得知他们三人包揽了这次竞赛的前三名,未告知具体名次,但提供了以下3条信息:①false不是第一名;②false不是第三名;③false是第三名,并告知他们这3条信息中有且只有一条信息正确,那么该次竞赛的第一名,第二名,第三名依次为( ).
A.false、false、false B.false、false、false C、false、false、false D.false、false、false
9.为解决问题:求使false成立的最大整数false,李小茶同学设计如下程序框图,其中能解决该问题的是( ).
A. B. C. D.
10.若实数系一元二次方程false在复数集false内的根为false,false,则有false,所以false,false(韦达定理),类比此方法求解如下问题:设实数系一元三次方程false在复数集false内的根为false,false,false,则false的值为( ).
A.false B.false C.false D.false
11.设复数false(false为虚数单位),若对任意实数false,false,则实数false的取值范围为( ).
A.false B.false C.false D.false
12.分形几何学是数学家伯努瓦·曼德尔布罗在20世纪70年代创立的一门新的数学学科,分形几何学不仅让人们感悟到数学与艺术审美的统一,而且还有其深刻的科学方法论意义.按照如图甲所示的分形规律可得如图乙所示的一个树形图.记图乙中第false行白圈的个数为false,黑圈的个数为false,则下列结论错误的是( ).
A.false
B.40是数列false中的项
C.对任意的false,均有false
D.false
二、填空题
13.若false(false,false),则false______.
14.用模型false拟合一组数据时,为了求出回归方程,设false,其变换后得到线性回归方程false,则false______.
15.false,false.通过观察上述两等式的共同规律,请你写出一个一般性的命题______.
16.已知false,false为正实数,若false,则false的最小值为______.
三、解答题
(一)必考题
17.某超市为提高服务质量,随机调查了60名男顾客和60名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意
不满意
合计
男顾客
48
女顾客
24
合计
(1)完成上述列联表,并估计顾客不满意的概率;
(2)判断能否有false的把握认为男、女顾客对该商场服务的评价有差异?
附:false,false.
false
0.050
0.010
0.001
false
3.841
6.635
10.828
18.以下是某地搜集到的新房屋的销售价格false(单位:百万元)和房屋的面积false(单位:false)的数据:
房屋面积(false)
120
110
105
90
80
销售价格(百万元)
3.6
3.41
3.23
2.82
2.53
(1)画出该组数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为false时的销售价格(结果精确到0.001).
附:false,false.
19.已知复数false,false,false.
(1)若false为实数,求角false的值;
(2)若复数false,false对应的向量分别是false,false,存在false使等式false成立,求实数false的取值范围.
20.(1)已知false,证明:false;
(2)已知false,且false,用分析法证明:false.
21.已知false,false是椭圆false:false(false)的左、右顶点,false为椭圆上异于false,false的点.
(1)证明:false的斜率与false的斜率之积为定值;
(2)探讨若false,false为椭圆false上关于原点对称的两点,false仍为false上异于false,false的点,若false的斜率和false的斜率都存在,是否仍有(1)中的结论呢?请说明理由;
(3)类比椭圆中的结论,双曲线false:false(false,false)中是否具有类似(1)的结论,若有,写出该定值(不必证明);若没有,请简要说明理由.
(二)选考题
22.在平面直角坐标系false中,曲线false的参数方程为false(false为参数),以false为极点,false轴的正半轴为极轴建立极坐标系,直线false的极坐标方程为false.
(1)求曲线false的普通方程及直线false的直角坐标方程;
(2)若直线false与曲线false的交点为false,false,与false轴的交点为false,求false的值.
23.已知false(false).
(1)若false,求不等式false的解集;
(2)若对任意false,关于false的不等式false恒成立,求false的取值范围.
商周联盟2020-2021学年高二下学期期末联考
数学试卷(文科)
参考答案、提示及评分细则
1.【答案】C
【解析】由题意,得false,所以false.故选C.
2.【答案】D
【解析】由组织结构图易知销售部的直接领导为副总经理二.故选D.
3.【答案】B
【解析】三段论的推理模式为:大前提,小前提,结论,故选B.
4.【答案】C
【解析】由表格数据知:false,false,由回归直线方程的性质,得false,所以false,故false,所以当false万元时,false万元.故选C.
5.【答案】D
【解析】反证假设为结论的否定,故假设应为false,false,false无正数.故选D.
6.【答案】A
【解析】①错误,例如false,false满足false,但false,false;②错误,例如false,false,满足条件,但二者是虚数,不能比较大小;③错误,等号左边结果一定是非负实数,等号右边未必是实数;④正确;⑤错误,类似于③.故选A.
7.【答案】A
【解析】我们可以用false的大小近似的判断两个分类变量之间关系的强弱,false的值越小,关系越弱,越大,关系越强.这四组数据中false的值分别为18、7、2、0,所以false组数据的false的值最大,相比较而言这组数据反应的false和false的关系最强.故选A.
8.【答案】B
【解析】由题意知若③对,则②也对,不合题意,故③一定错误,则false为第一名,或为第二名,若false为第一名,则①正确,那么②错误,故false为第三名,符合题意;若false为第二名,此时①②同真,或同假,不合题意.故选B.
9.【答案】B
【解析】假设满足条件的最大整数为false,按照四个框图的特点,执行false,并且此时还是满足判断框,继续循环,执行求和及计数变量再加1后,判断应不满足条件,退出循环,因为此时false比false大2,输出结果为false,故选B.
10.【答案】A
【解析】由false
false,
由对应系数相等,得false,false,所以false,false,所以false.故选A.
11.【答案】D
【解析】由false,得false,由复数模的几何意义知,false表示复平面上的点false与点false间的距离,点false在单位圆false上,要使false恒成立,则点false必在圆false上或其内部,故false,解得false.故选D.
12.【答案】C
【解析】根据图甲所示的分形规律,1个白圈分形为2个白圈1个黑圈,1个黑圈分形为1个白圈2个黑圈,第一行记为false,第二行记为false,第三行记为false,第四行的白圈数为false;黑圈数为false,故第四行的“坐标”为false,即false,A正确;第五行的“坐标”为false,即40是数列false中的项,B正确;各行白圈数乘以2,分别是2,4,10,28,82,即false,false,false,false,false,故第false行的白圈数为false,黑圈数为false,因为false,false,故C错误;因为false,故D正确.故选C.
13.【答案】1
【解析】false(false,false),即false,所以false,解得false,所以false.
14.【答案】false
【解析】由false,得false,故false,所以false.
15.【答案】false(答案不唯一)
【解析】由已知:false,false,归纳推理的一般性的命题为false.证明如下:
左边false
false右边.结论正确.
故答案为false.
16.【答案】9
【解析】false,当且仅当false时等号成立.故false的最小值为9.
17.【答案】解:(1)
满意
不满意
合计
男顾客
48
12
60
女顾客
36
24
60
合计
84
36
120
顾客不满意的频率为false,所以顾客不满意的概率估计为false.
(2)false,
所以能有false的把握认为男、女顾客对该商场服务的评价有差异.
【解析】
18.【答案】解:(1)数据对应的散点图如图所示:
(2)false,false,
false,false,
则false,
false,
故所求回归直线方程为false.
(3)据(2),当false时,销售价格的估计值为:
false(百万元).
【解析】
19.【答案】解:(1)false,
∴false,
又false,∴false,即false.
(2)false,
false,
false.
得false,
整理得false.
因为false,所以false.只要false即可,
解得false或false.
【解析】
20.【答案】证明:(1)因为false,
所以false,
所以false.
(2)因为false,且false,所以false,false,false,
要证false,只需证false即可,
只要证false,即证false,
只要证false,
因为false,false,false,所以false,false,
所以false成立,命题得证.
【解析】
21.【答案】证明:(1)设点false的坐标为false,由题意,知false,false,
所以false,false,
所以false.
因为点false在椭圆false上,所以false,
所以false(定值).
(2)设false,则false但
所以false的斜率false,
false的斜率false,
所以false.
又点false,false都在椭圆false上,所以false,false,
所以false(定值).
即结论仍成立.
(3)在双曲线false:false(false,false)中,若false,false为双曲线false的左右顶点,点false为其上异于false,false的一点,则false的斜率与false的斜率之积为定值false.
【解析】
22.【答案】解:(1)由false,得false,消去参数,得false,即曲线false的普通方程为false;
由false,得false,即false,
又false,false,所以false,
所以直线false的直角坐标方程为false.
(2)因为直线false的方程为false,所以直线false的参数方程为false(false为参数),
将其代入曲线false的方程,得false,
所以false,设false,false两点对应的参数分别为false,false,则
false,false.
所以false.
【解析】
23.【答案】解:(1)false时,false,
所以,当false时,不等式变为false,解得false;
当false时,不等式变为false,不等式无解;
当false时,不等式变为false,解得false.
所以原不等式的解集为false.
(2)因为false,当且仅当false时等号成立,
所以false.
由题意知false,
所以false,或false,
所以false,或false.
所以false的取值范围为false.
数学试卷(文科)
一、选择题
1.若复数false满足false(false为虚数单位),则false( ).
A.false B.false C.false D.false
2.如图是某公司的组织结构图,则销售部的直接上位领导是( ).
A.董事会 B.总经理 C.副总经理一 D.副总经理二
3.下列三段话,按演绎推理的三段论模式,排列顺序正确的是( ).
①false,false是两个实数;②任意两个实数之间能比较大小;③false,false之间能比较大小
A.①②③ B.②①③ C.③②① D.②③①
4.某产品的宣传费用false(单位:万元)与销售额false(单位:万元)的统计数据如表所示:
false
4
5
6
7
8
false
60
80
90
100
120
根据上表可得回归直线方程false,则宣传费用为9万元时,销售额约为( ).
A.123万元 B.128万元 C.132万元 D.138万元
5.用反证法证明问题“false,false,false,若false,则false,false,false中至少有一个正数”时,假设为( ).
A.false,false,false均为负数 B.false,false,false中至多一个是正数
C.false,false,false均为正数 D.false,false,false中没有正数
6.已知复数false,false,则下列结论:①若false,则false;②若false,则false;③false;④false;⑤false正确的个数为( ).
A.1 B.2 C.3 D.4
7.两个分类变量false和false,它们的取值分别为false和false,其样本频数列联表如下表所示:
false
false
合计
false
false
false
false
false
false
false
false
合计
false
false
false
则下列四组数据中,分类变量false和false之间关系最强的是( ).
A.false,false,false,false B.false,false,false,false
C.false,false,false,false D.false,false,false,false
8.false,false,false三人参加单位组织的安全生产知识(闭卷)竞赛,三人向组织人员询问结果,得知他们三人包揽了这次竞赛的前三名,未告知具体名次,但提供了以下3条信息:①false不是第一名;②false不是第三名;③false是第三名,并告知他们这3条信息中有且只有一条信息正确,那么该次竞赛的第一名,第二名,第三名依次为( ).
A.false、false、false B.false、false、false C、false、false、false D.false、false、false
9.为解决问题:求使false成立的最大整数false,李小茶同学设计如下程序框图,其中能解决该问题的是( ).
A. B. C. D.
10.若实数系一元二次方程false在复数集false内的根为false,false,则有false,所以false,false(韦达定理),类比此方法求解如下问题:设实数系一元三次方程false在复数集false内的根为false,false,false,则false的值为( ).
A.false B.false C.false D.false
11.设复数false(false为虚数单位),若对任意实数false,false,则实数false的取值范围为( ).
A.false B.false C.false D.false
12.分形几何学是数学家伯努瓦·曼德尔布罗在20世纪70年代创立的一门新的数学学科,分形几何学不仅让人们感悟到数学与艺术审美的统一,而且还有其深刻的科学方法论意义.按照如图甲所示的分形规律可得如图乙所示的一个树形图.记图乙中第false行白圈的个数为false,黑圈的个数为false,则下列结论错误的是( ).
A.false
B.40是数列false中的项
C.对任意的false,均有false
D.false
二、填空题
13.若false(false,false),则false______.
14.用模型false拟合一组数据时,为了求出回归方程,设false,其变换后得到线性回归方程false,则false______.
15.false,false.通过观察上述两等式的共同规律,请你写出一个一般性的命题______.
16.已知false,false为正实数,若false,则false的最小值为______.
三、解答题
(一)必考题
17.某超市为提高服务质量,随机调查了60名男顾客和60名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意
不满意
合计
男顾客
48
女顾客
24
合计
(1)完成上述列联表,并估计顾客不满意的概率;
(2)判断能否有false的把握认为男、女顾客对该商场服务的评价有差异?
附:false,false.
false
0.050
0.010
0.001
false
3.841
6.635
10.828
18.以下是某地搜集到的新房屋的销售价格false(单位:百万元)和房屋的面积false(单位:false)的数据:
房屋面积(false)
120
110
105
90
80
销售价格(百万元)
3.6
3.41
3.23
2.82
2.53
(1)画出该组数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为false时的销售价格(结果精确到0.001).
附:false,false.
19.已知复数false,false,false.
(1)若false为实数,求角false的值;
(2)若复数false,false对应的向量分别是false,false,存在false使等式false成立,求实数false的取值范围.
20.(1)已知false,证明:false;
(2)已知false,且false,用分析法证明:false.
21.已知false,false是椭圆false:false(false)的左、右顶点,false为椭圆上异于false,false的点.
(1)证明:false的斜率与false的斜率之积为定值;
(2)探讨若false,false为椭圆false上关于原点对称的两点,false仍为false上异于false,false的点,若false的斜率和false的斜率都存在,是否仍有(1)中的结论呢?请说明理由;
(3)类比椭圆中的结论,双曲线false:false(false,false)中是否具有类似(1)的结论,若有,写出该定值(不必证明);若没有,请简要说明理由.
(二)选考题
22.在平面直角坐标系false中,曲线false的参数方程为false(false为参数),以false为极点,false轴的正半轴为极轴建立极坐标系,直线false的极坐标方程为false.
(1)求曲线false的普通方程及直线false的直角坐标方程;
(2)若直线false与曲线false的交点为false,false,与false轴的交点为false,求false的值.
23.已知false(false).
(1)若false,求不等式false的解集;
(2)若对任意false,关于false的不等式false恒成立,求false的取值范围.
商周联盟2020-2021学年高二下学期期末联考
数学试卷(文科)
参考答案、提示及评分细则
1.【答案】C
【解析】由题意,得false,所以false.故选C.
2.【答案】D
【解析】由组织结构图易知销售部的直接领导为副总经理二.故选D.
3.【答案】B
【解析】三段论的推理模式为:大前提,小前提,结论,故选B.
4.【答案】C
【解析】由表格数据知:false,false,由回归直线方程的性质,得false,所以false,故false,所以当false万元时,false万元.故选C.
5.【答案】D
【解析】反证假设为结论的否定,故假设应为false,false,false无正数.故选D.
6.【答案】A
【解析】①错误,例如false,false满足false,但false,false;②错误,例如false,false,满足条件,但二者是虚数,不能比较大小;③错误,等号左边结果一定是非负实数,等号右边未必是实数;④正确;⑤错误,类似于③.故选A.
7.【答案】A
【解析】我们可以用false的大小近似的判断两个分类变量之间关系的强弱,false的值越小,关系越弱,越大,关系越强.这四组数据中false的值分别为18、7、2、0,所以false组数据的false的值最大,相比较而言这组数据反应的false和false的关系最强.故选A.
8.【答案】B
【解析】由题意知若③对,则②也对,不合题意,故③一定错误,则false为第一名,或为第二名,若false为第一名,则①正确,那么②错误,故false为第三名,符合题意;若false为第二名,此时①②同真,或同假,不合题意.故选B.
9.【答案】B
【解析】假设满足条件的最大整数为false,按照四个框图的特点,执行false,并且此时还是满足判断框,继续循环,执行求和及计数变量再加1后,判断应不满足条件,退出循环,因为此时false比false大2,输出结果为false,故选B.
10.【答案】A
【解析】由false
false,
由对应系数相等,得false,false,所以false,false,所以false.故选A.
11.【答案】D
【解析】由false,得false,由复数模的几何意义知,false表示复平面上的点false与点false间的距离,点false在单位圆false上,要使false恒成立,则点false必在圆false上或其内部,故false,解得false.故选D.
12.【答案】C
【解析】根据图甲所示的分形规律,1个白圈分形为2个白圈1个黑圈,1个黑圈分形为1个白圈2个黑圈,第一行记为false,第二行记为false,第三行记为false,第四行的白圈数为false;黑圈数为false,故第四行的“坐标”为false,即false,A正确;第五行的“坐标”为false,即40是数列false中的项,B正确;各行白圈数乘以2,分别是2,4,10,28,82,即false,false,false,false,false,故第false行的白圈数为false,黑圈数为false,因为false,false,故C错误;因为false,故D正确.故选C.
13.【答案】1
【解析】false(false,false),即false,所以false,解得false,所以false.
14.【答案】false
【解析】由false,得false,故false,所以false.
15.【答案】false(答案不唯一)
【解析】由已知:false,false,归纳推理的一般性的命题为false.证明如下:
左边false
false右边.结论正确.
故答案为false.
16.【答案】9
【解析】false,当且仅当false时等号成立.故false的最小值为9.
17.【答案】解:(1)
满意
不满意
合计
男顾客
48
12
60
女顾客
36
24
60
合计
84
36
120
顾客不满意的频率为false,所以顾客不满意的概率估计为false.
(2)false,
所以能有false的把握认为男、女顾客对该商场服务的评价有差异.
【解析】
18.【答案】解:(1)数据对应的散点图如图所示:
(2)false,false,
false,false,
则false,
false,
故所求回归直线方程为false.
(3)据(2),当false时,销售价格的估计值为:
false(百万元).
【解析】
19.【答案】解:(1)false,
∴false,
又false,∴false,即false.
(2)false,
false,
false.
得false,
整理得false.
因为false,所以false.只要false即可,
解得false或false.
【解析】
20.【答案】证明:(1)因为false,
所以false,
所以false.
(2)因为false,且false,所以false,false,false,
要证false,只需证false即可,
只要证false,即证false,
只要证false,
因为false,false,false,所以false,false,
所以false成立,命题得证.
【解析】
21.【答案】证明:(1)设点false的坐标为false,由题意,知false,false,
所以false,false,
所以false.
因为点false在椭圆false上,所以false,
所以false(定值).
(2)设false,则false但
所以false的斜率false,
false的斜率false,
所以false.
又点false,false都在椭圆false上,所以false,false,
所以false(定值).
即结论仍成立.
(3)在双曲线false:false(false,false)中,若false,false为双曲线false的左右顶点,点false为其上异于false,false的一点,则false的斜率与false的斜率之积为定值false.
【解析】
22.【答案】解:(1)由false,得false,消去参数,得false,即曲线false的普通方程为false;
由false,得false,即false,
又false,false,所以false,
所以直线false的直角坐标方程为false.
(2)因为直线false的方程为false,所以直线false的参数方程为false(false为参数),
将其代入曲线false的方程,得false,
所以false,设false,false两点对应的参数分别为false,false,则
false,false.
所以false.
【解析】
23.【答案】解:(1)false时,false,
所以,当false时,不等式变为false,解得false;
当false时,不等式变为false,不等式无解;
当false时,不等式变为false,解得false.
所以原不等式的解集为false.
(2)因为false,当且仅当false时等号成立,
所以false.
由题意知false,
所以false,或false,
所以false,或false.
所以false的取值范围为false.
同课章节目录
