《1.1探索勾股定理》自主学习优生提升训练(附答案)2021-2022学年八年级数学北师大版上册(word版含解析)
文档属性
| 名称 | 《1.1探索勾股定理》自主学习优生提升训练(附答案)2021-2022学年八年级数学北师大版上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 21:44:49 | ||
图片预览


文档简介
2021年北师大版八年级数学上册《1.1探索勾股定理》自主学习优生提升训练(附答案)
1.如图,a,b,c是3×3正方形网格中的3条线段,它们端点都在格点上,则关于a,b,c大小关系的正确判断是( )
A.b<a<c B.a<b<c C.a<c<b D.b<c<a
2.一直角三角形的一条直角边长是6,另一条直角边与斜边长的和是18,则直角三角形的面积是( )
A.8 B.48 C.24 D.30
3.如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且,且S1=4,S3=16,则S2=( )
A.20 B.12 C.2 D.2
4.若直角三角形的三边长分别为2,4,x,则x的值为( )
A.3 B. C.2 D.或2
5.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,若AD是△ABC的高,则AD的长为( )
A.2 B. C. D.2
6.如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是( )
A. B. C. D.
7.已知一个直角三角形的两条边的长分别为3和4,则它的第三条边是( )
A.5或 B. C.5 D.2或5
8.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.
9.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 .
10.如图,线段CE的长为3cm,延长EC到B,以CB为一边作正方形ABCD,连接DE,以DE为一边作正方形DEFG,设正方形ABCD的面积为S1,正方形DEFG的面积为S2,则S2﹣S1的值为 .
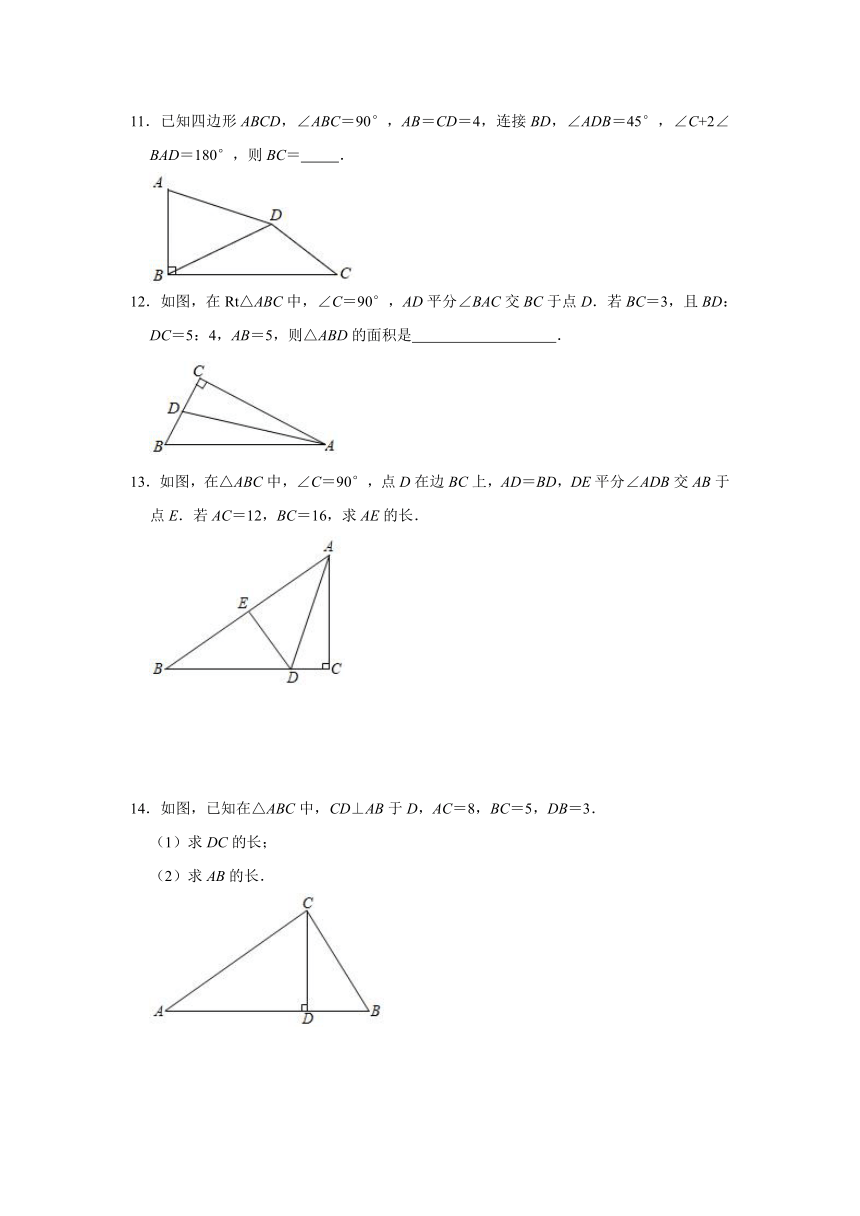
11.已知四边形ABCD,∠ABC=90°,AB=CD=4,连接BD,∠ADB=45°,∠C+2∠BAD=180°,则BC= .
12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BC=3,且BD:DC=5:4,AB=5,则△ABD的面积是 .
13.如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,求AE的长.
14.如图,已知在△ABC中,CD⊥AB于D,AC=8,BC=5,DB=3.
(1)求DC的长;
(2)求AB的长.
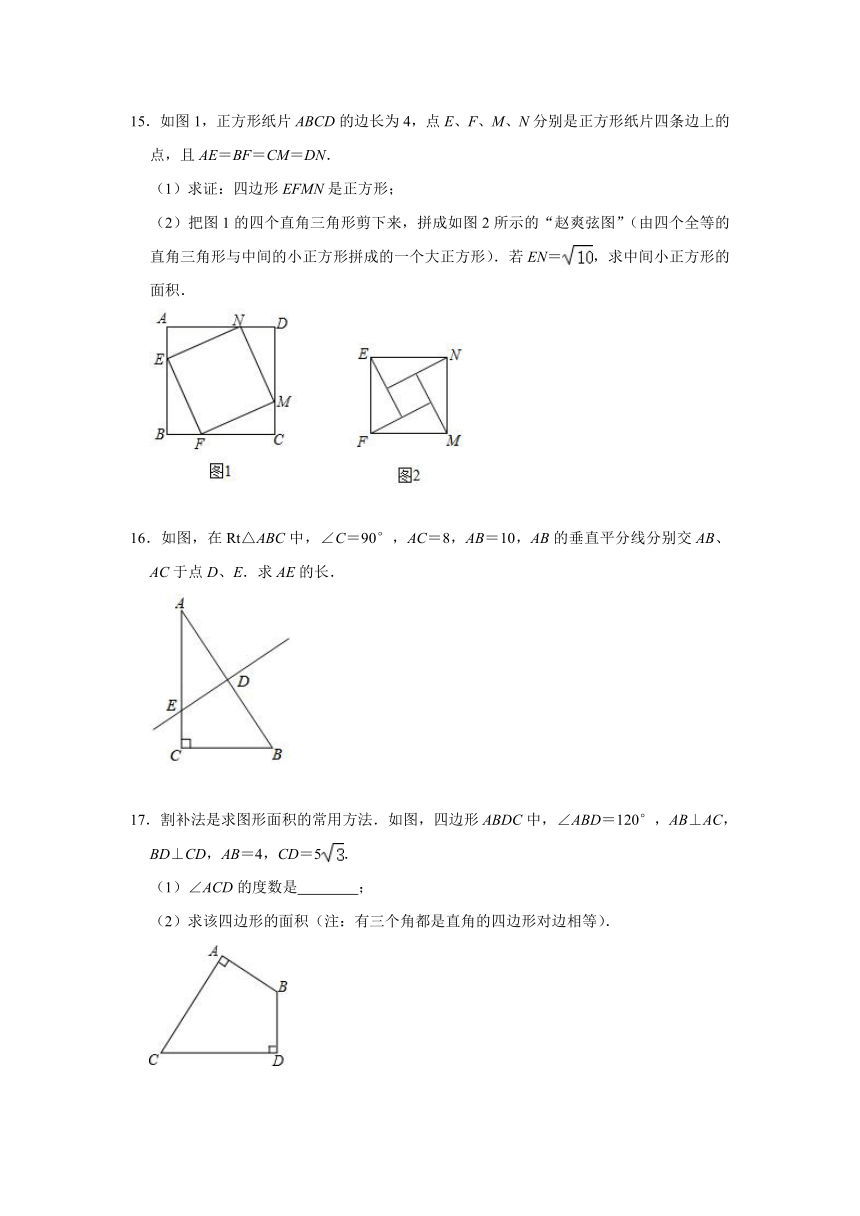
15.如图1,正方形纸片ABCD的边长为4,点E、F、M、N分别是正方形纸片四条边上的点,且AE=BF=CM=DN.
(1)求证:四边形EFMN是正方形;
(2)把图1的四个直角三角形剪下来,拼成如图2所示的“赵爽弦图”(由四个全等的直角三角形与中间的小正方形拼成的一个大正方形).若EN=,求中间小正方形的面积.
16.如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,AB的垂直平分线分别交AB、AC于点D、E.求AE的长.
17.割补法是求图形面积的常用方法.如图,四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,AB=4,CD=5.
(1)∠ACD的度数是 ;
(2)求该四边形的面积(注:有三个角都是直角的四边形对边相等).
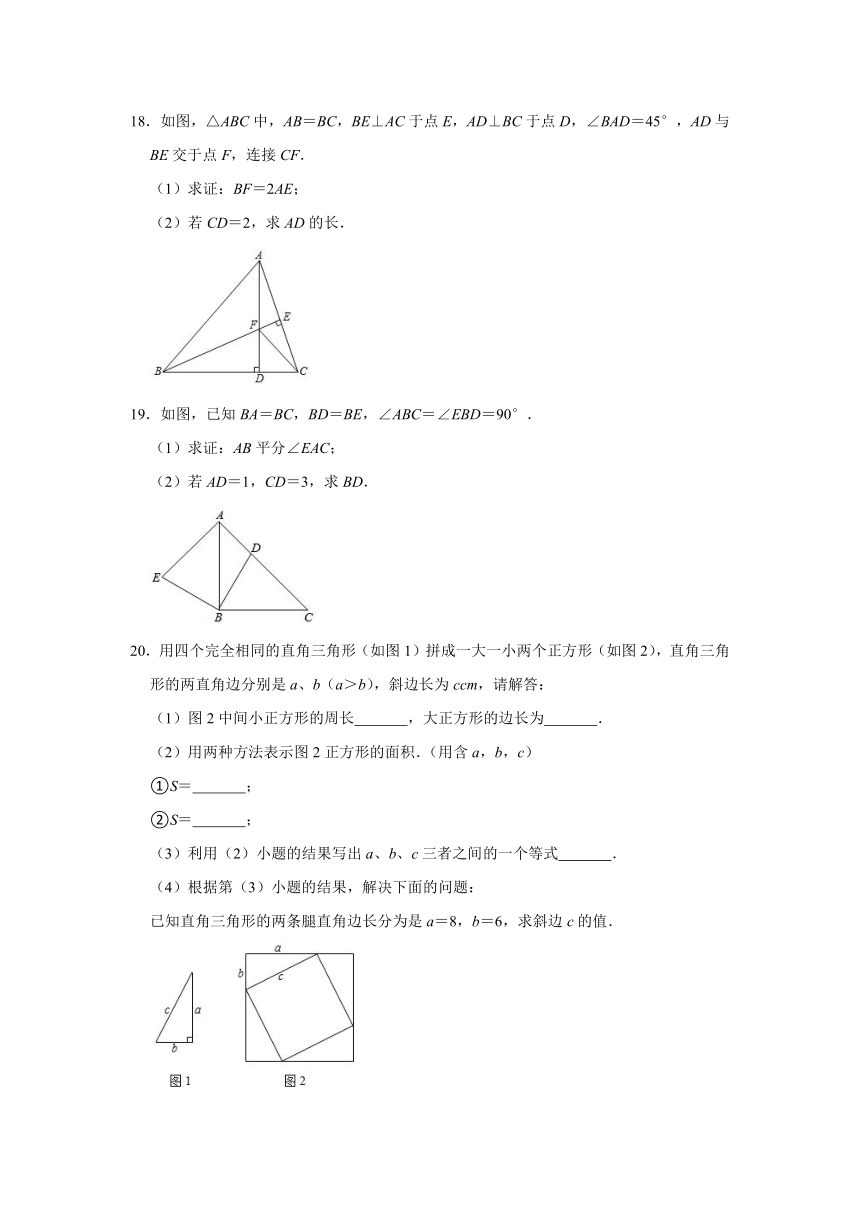
18.如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=2,求AD的长.
19.如图,已知BA=BC,BD=BE,∠ABC=∠EBD=90°.
(1)求证:AB平分∠EAC;
(2)若AD=1,CD=3,求BD.
20.用四个完全相同的直角三角形(如图1)拼成一大一小两个正方形(如图2),直角三角形的两直角边分别是a、b(a>b),斜边长为ccm,请解答:
(1)图2中间小正方形的周长 ,大正方形的边长为 .
(2)用两种方法表示图2正方形的面积.(用含a,b,c)
①S= ;
②S= ;
(3)利用(2)小题的结果写出a、b、c三者之间的一个等式 .
(4)根据第(3)小题的结果,解决下面的问题:
已知直角三角形的两条腿直角边长分为是a=8,b=6,求斜边c的值.
参考答案
1.解:由题意得a=,
b=,
c=,
∴a<b<c,
故选:B.
2.解:设另一直角边的长为x,则斜边为18﹣x,
∵直角三角形的一条直角边长是6,
∴62+x2=(18﹣x)2,
解得x=8.
∴直角三角形的面积为=24
故选:C.
3.解:由勾股定理得,AC2=AB2﹣BC2=16﹣4=12,
则S2=AC2=12,
故选:B.
4.解:①当x为斜边时,x2=22+42=20,所以x=2;
②当4为斜边时,x2=16﹣4=12,x=2.
故选:D.
5.解:∵AB2=22+42=4+16=20;
AC2=22+12=4+1=5,
BC2=32+42=9+16=25,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∴S△BAC=AB×AC=××=5,
∵同一三角形面积相等,
S△BAC=BC?AD=×5×AD=5,
∴AD=2.
故选:D.
6.解:在Rt△ABC中,AC=4,AB=5,∠C=90°,
∴BC==3,
过D作DE⊥AB于E,
∵BD平分∠ABC,∠C=90°,
∴CD=DE,
在Rt△BCD与Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴BE=BC=3,
∴AE=2,
∵AD2=DE2+AE2,
∴DE2+22=(4﹣DE)2,
∴DE=,
∴BD===.
故选:D.
7.解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理,得
32+42=x2,所以x=5.
(2)若4是斜边,则第三边x为直角边,由勾股定理,得
32+x2=42,所以x=
所以第三边的长为5或.
故选:A.
8.解:依题意画出图形,
设芦苇长AC=AC′=x尺,
则水深AB=(x﹣1)尺,
∵C′E=10尺,
∴C′B=5尺,
在Rt△AC′B中,
52+(x﹣1)2=x2,
解得x=13,
即芦苇长13尺,水深为12尺,
故答案为:12.
9.解:直角三角形直角边的较短边为=6,
正方形EFGH的面积=10×10﹣8×6÷2×4=100﹣96=4.
故答案为:4.
10.解:∵S1=DC2,S2=DE2,
正方形ABCD中DC⊥BC,
∴∠DCE=90°,
在Rt△DCE中,
DE2=DC2+CE2,
∴S2=S1+CE2,
即S2﹣S1=CE2=9.
故答案为:9.
11.解:过B作BO⊥AD于O,交CD的延长线于E,
∵BE⊥AD,∠ADB=45°,
∴∠OBD=45°,
∴OB=OD,
∵∠A+∠EBA=90°,
∠ABE+∠EBC=90°,
∴∠A=∠EBC,
∵∠C+2∠BAD=180°,∠C+∠E+∠EBC=180°,
∴∠E=∠EBC=∠A,
∴BC=CE,
在△ABO和△EDO中,
,
∴△ABO≌△EDO(AAS),
∴AB=DE,
∴CE=CD+DE=2×4=8,
∵BC=CE,
∴BC=8,
故答案为:8.
12.解:作DE⊥AB于点E,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DC=DE,
∵BC=3,且BD:DC=5:4,
∴DC=3×=,
∴DE=,
∵AB=5,DE⊥AB,
∴△ABD的面积是:==,
故答案为:.
13.解:如图,在△ABC中,∠C=90°,AC=12,BC=16,
由勾股定理知:AB===20.
∵AD=BD,DE平分∠ADB交AB于点E.
∴AE=BE=AB=10.
14.解:(1)∵CD⊥AB于D,BC=5,DB=3,
∴在Rt△BCD中,CD2=CB2﹣DB2=52﹣32=16,
∴CD=4.
(2)在Rt△ACD中,AD2=AC2﹣CD2=82﹣42=48,
∴AD=4,
∴AB=AD+DB=4+3.
15.(1)证明:如图1∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,
∵AE=BF=CM=DN,
∴AN=DM=CF=BE,
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DMN≌△CFM≌△BEF(SAS),
∴EN=NM=MF=EF,∠ENA=∠DMN,
∴四边形EFMN是菱形,
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°,
∴∠ENM=90°,
∴四边形EFMN是正方形;
(2)解:∵△AEN≌△DMN≌△CFM≌△BEF,
∴EF=FM=MN=NE,EH=FG=MR=NQ,EQ=FH=MG=NR,
如图2,设正方形EFMN的边长EF=FM=MN=NE=c,EH=FG=MR=NQ=b,EQ=FH=MG=NR=a,
则小正方形QHGR的边长QH=b﹣a,
∴小正方形QHGR的面积为(b﹣a)2=a2+b2﹣2ab,
∴由勾股定理得:a2+b2=c2=EN2=10,
∵正方形ABCD的边长为4,
∴a+b=4,
∴a2+b2+2ab=16,
∴2ab=16﹣(a2+b2)=6,
∴中间小正方形QHGR的面积为10﹣6=4.
16.解:在Rt△ABC中,∠C=90°,AC=8,AB=10,
∴BC===6,
连接BE,
∵DE垂直平分AB,
∴AE=BE,
设AE=BE=x,则CE=8﹣x,
在Rt△BCE中,∵BC2+CE2=BE2,
∴62+(8﹣x)2=x2,
解得x=,
∴AE=.
17.解:(1)∵四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,
∴∠ACD=60°,
故答案为60°;
(2)如图,延长CA、DB交于点E,
由(1)可知∠E=30°.
在Rt△ABE中,
∵AB=4,∠E=30°,
∴BE=2AB=8,
∴AE===4,
在Rt△DEC中,∵∠E=30°,CD=5,
∴CE=2CD=10,
∴DE===15,
∴S△ABE=×4×4=8,
S△CDE=×5×15=,
∴S四边形ABDC=S△CDE﹣S△ABE=.
18.(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,
∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)解:∵△ADC≌△BDF,
∴DF=CD=2,
在Rt△CDF中,CF===2,
∵BE⊥AC,AE=EC,
∴AF=CF=2,
∴AD=AF+DF=2+2.
19.解:(1)证明:∵∠ABC=∠EBD=90°,
∴∠ABD+∠CBD=∠ABD+∠ABE,
∴∠CBD=∠ABE,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴∠EAB=∠BAC,
∴AB平分∠EAC;
(2)∵AD=1,CD=3,
∴AC=4.
∵BA=BC,∠ABC=90°,
∴AB=BC==2,∠C=45°,
过点B作BF⊥AC于点F,如图:
则△BCF为等腰直角三角形,
∴BF=CF=2,
∴DF=CD﹣CF=1,
在Rt△BFD中,由勾股定理得:
BD=
=
=.
∴BD的长等于.
20.解:(1)图2中间小正方形的周长4c,大正方形的边长为(a+b),
故答案为:4c;a+b;
(2)图2正方形的面积S=(a+b)2或S=2ab+c2,
故答案为:(a+b)2或2ab+c2;
(3)∵(a+b)2=a2+2ab+b2,
∴a2+b2=c2.
故答案为:a2+b2=c2;
(4)∵c2=a2+b2=82+62=100,
∴c=10(负值不合题意,舍去).
1.如图,a,b,c是3×3正方形网格中的3条线段,它们端点都在格点上,则关于a,b,c大小关系的正确判断是( )
A.b<a<c B.a<b<c C.a<c<b D.b<c<a
2.一直角三角形的一条直角边长是6,另一条直角边与斜边长的和是18,则直角三角形的面积是( )
A.8 B.48 C.24 D.30
3.如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且,且S1=4,S3=16,则S2=( )
A.20 B.12 C.2 D.2
4.若直角三角形的三边长分别为2,4,x,则x的值为( )
A.3 B. C.2 D.或2
5.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,若AD是△ABC的高,则AD的长为( )
A.2 B. C. D.2
6.如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是( )
A. B. C. D.
7.已知一个直角三角形的两条边的长分别为3和4,则它的第三条边是( )
A.5或 B. C.5 D.2或5
8.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.
9.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 .
10.如图,线段CE的长为3cm,延长EC到B,以CB为一边作正方形ABCD,连接DE,以DE为一边作正方形DEFG,设正方形ABCD的面积为S1,正方形DEFG的面积为S2,则S2﹣S1的值为 .
11.已知四边形ABCD,∠ABC=90°,AB=CD=4,连接BD,∠ADB=45°,∠C+2∠BAD=180°,则BC= .
12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BC=3,且BD:DC=5:4,AB=5,则△ABD的面积是 .
13.如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,求AE的长.
14.如图,已知在△ABC中,CD⊥AB于D,AC=8,BC=5,DB=3.
(1)求DC的长;
(2)求AB的长.
15.如图1,正方形纸片ABCD的边长为4,点E、F、M、N分别是正方形纸片四条边上的点,且AE=BF=CM=DN.
(1)求证:四边形EFMN是正方形;
(2)把图1的四个直角三角形剪下来,拼成如图2所示的“赵爽弦图”(由四个全等的直角三角形与中间的小正方形拼成的一个大正方形).若EN=,求中间小正方形的面积.
16.如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,AB的垂直平分线分别交AB、AC于点D、E.求AE的长.
17.割补法是求图形面积的常用方法.如图,四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,AB=4,CD=5.
(1)∠ACD的度数是 ;
(2)求该四边形的面积(注:有三个角都是直角的四边形对边相等).
18.如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=2,求AD的长.
19.如图,已知BA=BC,BD=BE,∠ABC=∠EBD=90°.
(1)求证:AB平分∠EAC;
(2)若AD=1,CD=3,求BD.
20.用四个完全相同的直角三角形(如图1)拼成一大一小两个正方形(如图2),直角三角形的两直角边分别是a、b(a>b),斜边长为ccm,请解答:
(1)图2中间小正方形的周长 ,大正方形的边长为 .
(2)用两种方法表示图2正方形的面积.(用含a,b,c)
①S= ;
②S= ;
(3)利用(2)小题的结果写出a、b、c三者之间的一个等式 .
(4)根据第(3)小题的结果,解决下面的问题:
已知直角三角形的两条腿直角边长分为是a=8,b=6,求斜边c的值.
参考答案
1.解:由题意得a=,
b=,
c=,
∴a<b<c,
故选:B.
2.解:设另一直角边的长为x,则斜边为18﹣x,
∵直角三角形的一条直角边长是6,
∴62+x2=(18﹣x)2,
解得x=8.
∴直角三角形的面积为=24
故选:C.
3.解:由勾股定理得,AC2=AB2﹣BC2=16﹣4=12,
则S2=AC2=12,
故选:B.
4.解:①当x为斜边时,x2=22+42=20,所以x=2;
②当4为斜边时,x2=16﹣4=12,x=2.
故选:D.
5.解:∵AB2=22+42=4+16=20;
AC2=22+12=4+1=5,
BC2=32+42=9+16=25,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∴S△BAC=AB×AC=××=5,
∵同一三角形面积相等,
S△BAC=BC?AD=×5×AD=5,
∴AD=2.
故选:D.
6.解:在Rt△ABC中,AC=4,AB=5,∠C=90°,
∴BC==3,
过D作DE⊥AB于E,
∵BD平分∠ABC,∠C=90°,
∴CD=DE,
在Rt△BCD与Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴BE=BC=3,
∴AE=2,
∵AD2=DE2+AE2,
∴DE2+22=(4﹣DE)2,
∴DE=,
∴BD===.
故选:D.
7.解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理,得
32+42=x2,所以x=5.
(2)若4是斜边,则第三边x为直角边,由勾股定理,得
32+x2=42,所以x=
所以第三边的长为5或.
故选:A.
8.解:依题意画出图形,
设芦苇长AC=AC′=x尺,
则水深AB=(x﹣1)尺,
∵C′E=10尺,
∴C′B=5尺,
在Rt△AC′B中,
52+(x﹣1)2=x2,
解得x=13,
即芦苇长13尺,水深为12尺,
故答案为:12.
9.解:直角三角形直角边的较短边为=6,
正方形EFGH的面积=10×10﹣8×6÷2×4=100﹣96=4.
故答案为:4.
10.解:∵S1=DC2,S2=DE2,
正方形ABCD中DC⊥BC,
∴∠DCE=90°,
在Rt△DCE中,
DE2=DC2+CE2,
∴S2=S1+CE2,
即S2﹣S1=CE2=9.
故答案为:9.
11.解:过B作BO⊥AD于O,交CD的延长线于E,
∵BE⊥AD,∠ADB=45°,
∴∠OBD=45°,
∴OB=OD,
∵∠A+∠EBA=90°,
∠ABE+∠EBC=90°,
∴∠A=∠EBC,
∵∠C+2∠BAD=180°,∠C+∠E+∠EBC=180°,
∴∠E=∠EBC=∠A,
∴BC=CE,
在△ABO和△EDO中,
,
∴△ABO≌△EDO(AAS),
∴AB=DE,
∴CE=CD+DE=2×4=8,
∵BC=CE,
∴BC=8,
故答案为:8.
12.解:作DE⊥AB于点E,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DC=DE,
∵BC=3,且BD:DC=5:4,
∴DC=3×=,
∴DE=,
∵AB=5,DE⊥AB,
∴△ABD的面积是:==,
故答案为:.
13.解:如图,在△ABC中,∠C=90°,AC=12,BC=16,
由勾股定理知:AB===20.
∵AD=BD,DE平分∠ADB交AB于点E.
∴AE=BE=AB=10.
14.解:(1)∵CD⊥AB于D,BC=5,DB=3,
∴在Rt△BCD中,CD2=CB2﹣DB2=52﹣32=16,
∴CD=4.
(2)在Rt△ACD中,AD2=AC2﹣CD2=82﹣42=48,
∴AD=4,
∴AB=AD+DB=4+3.
15.(1)证明:如图1∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,
∵AE=BF=CM=DN,
∴AN=DM=CF=BE,
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DMN≌△CFM≌△BEF(SAS),
∴EN=NM=MF=EF,∠ENA=∠DMN,
∴四边形EFMN是菱形,
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°,
∴∠ENM=90°,
∴四边形EFMN是正方形;
(2)解:∵△AEN≌△DMN≌△CFM≌△BEF,
∴EF=FM=MN=NE,EH=FG=MR=NQ,EQ=FH=MG=NR,
如图2,设正方形EFMN的边长EF=FM=MN=NE=c,EH=FG=MR=NQ=b,EQ=FH=MG=NR=a,
则小正方形QHGR的边长QH=b﹣a,
∴小正方形QHGR的面积为(b﹣a)2=a2+b2﹣2ab,
∴由勾股定理得:a2+b2=c2=EN2=10,
∵正方形ABCD的边长为4,
∴a+b=4,
∴a2+b2+2ab=16,
∴2ab=16﹣(a2+b2)=6,
∴中间小正方形QHGR的面积为10﹣6=4.
16.解:在Rt△ABC中,∠C=90°,AC=8,AB=10,
∴BC===6,
连接BE,
∵DE垂直平分AB,
∴AE=BE,
设AE=BE=x,则CE=8﹣x,
在Rt△BCE中,∵BC2+CE2=BE2,
∴62+(8﹣x)2=x2,
解得x=,
∴AE=.
17.解:(1)∵四边形ABDC中,∠ABD=120°,AB⊥AC,BD⊥CD,
∴∠ACD=60°,
故答案为60°;
(2)如图,延长CA、DB交于点E,
由(1)可知∠E=30°.
在Rt△ABE中,
∵AB=4,∠E=30°,
∴BE=2AB=8,
∴AE===4,
在Rt△DEC中,∵∠E=30°,CD=5,
∴CE=2CD=10,
∴DE===15,
∴S△ABE=×4×4=8,
S△CDE=×5×15=,
∴S四边形ABDC=S△CDE﹣S△ABE=.
18.(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,
∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)解:∵△ADC≌△BDF,
∴DF=CD=2,
在Rt△CDF中,CF===2,
∵BE⊥AC,AE=EC,
∴AF=CF=2,
∴AD=AF+DF=2+2.
19.解:(1)证明:∵∠ABC=∠EBD=90°,
∴∠ABD+∠CBD=∠ABD+∠ABE,
∴∠CBD=∠ABE,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴∠EAB=∠BAC,
∴AB平分∠EAC;
(2)∵AD=1,CD=3,
∴AC=4.
∵BA=BC,∠ABC=90°,
∴AB=BC==2,∠C=45°,
过点B作BF⊥AC于点F,如图:
则△BCF为等腰直角三角形,
∴BF=CF=2,
∴DF=CD﹣CF=1,
在Rt△BFD中,由勾股定理得:
BD=
=
=.
∴BD的长等于.
20.解:(1)图2中间小正方形的周长4c,大正方形的边长为(a+b),
故答案为:4c;a+b;
(2)图2正方形的面积S=(a+b)2或S=2ab+c2,
故答案为:(a+b)2或2ab+c2;
(3)∵(a+b)2=a2+2ab+b2,
∴a2+b2=c2.
故答案为:a2+b2=c2;
(4)∵c2=a2+b2=82+62=100,
∴c=10(负值不合题意,舍去).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
