《1.4用一元二次方程解决问题》同步优生辅导训练(附答案)2021-2022学年九年级数学苏科版上册(word版含解析)
文档属性
| 名称 | 《1.4用一元二次方程解决问题》同步优生辅导训练(附答案)2021-2022学年九年级数学苏科版上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 157.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 21:50:37 | ||
图片预览




文档简介
2021年苏科版九年级数学上册《1.4用一元二次方程解决问题》同步优生辅导训练(附答案)
一.增长率问题
1.一种药品原价为25元,经过两次降价后每盒16元,设两次降价的百分率都同为x,则x满足方程( )
A.25(1﹣2x2)=16 B.25(1﹣x)2=16
C.16(1+2x2)=25 D.16(1+x)2=25
2.某超市一月份的营业额为25万元,三月份时因新冠疫情下降到16万元,若平均每月下降率为x,则由题意列方程应为( )
A.25(1+x)2=16 B.25(1﹣x)2=16
C.16(1+x)2=25 D.25[1+(1﹣x)+(1﹣x)2]=16
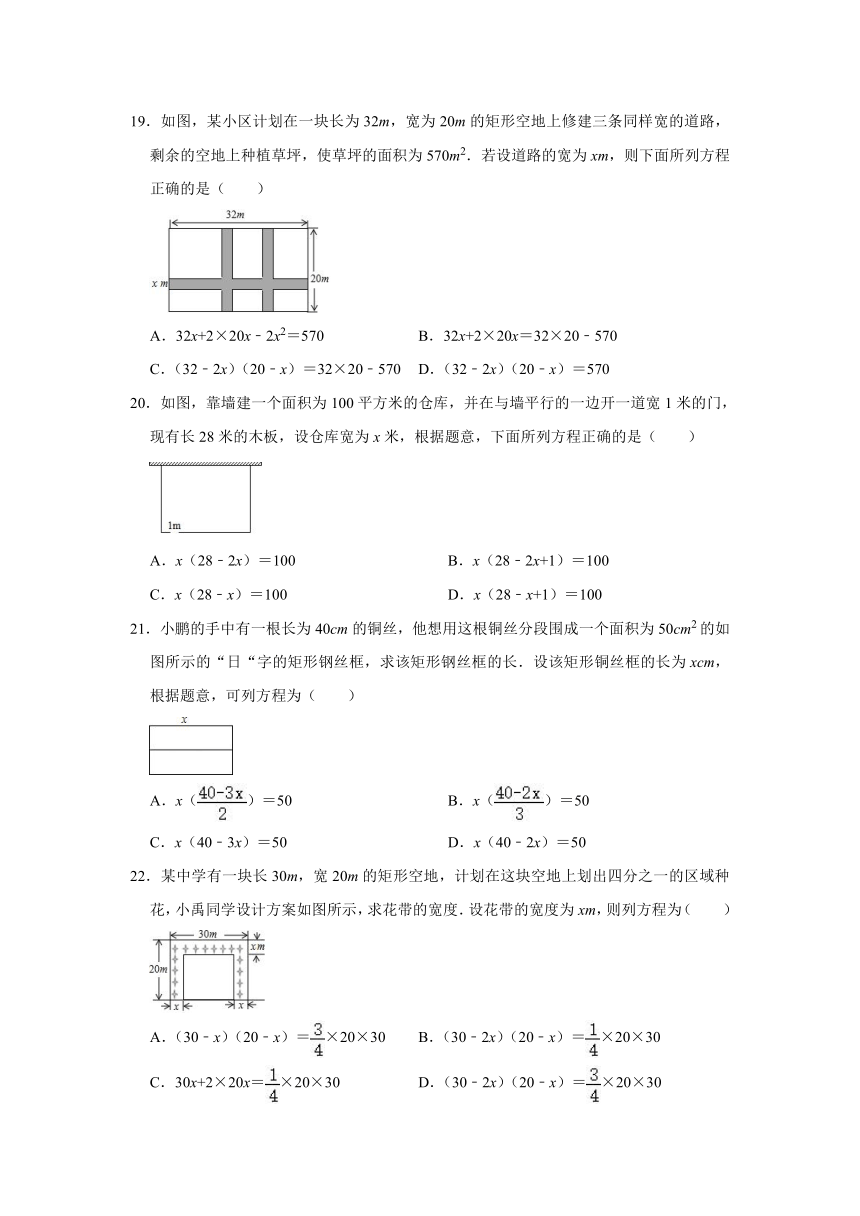
3.双十一来临前,某商场将一件衬衫的价格以一个给定的百分比提升,双十一那天商场又按照新的价格以相同的百分比降低了这件衬衫的价格,最终,衬衫的价格为原价的84%,则这个给定的百分比为( )
A.16% B.36% C.40% D.50%
4.为响应中央“房住不炒”的基本政策,某房企连续降价两次后的平均价格比降价之前减少了19%,则平均每次降价的百分率为( )
A.9.5% B.10% C.10.5% D.11%
5.某商贸公司2019年盈利100万元,2021年盈利144万元,且2019年到2021年每年盈利的增长率相同,则该公司2020年盈利 万元.
6.电影《中国机长》首映当日票房已经达到1.92亿元,2天后当日票房达到2.61亿元,设平均每天票房的增长率为x,则可列方程为 .
7.某工厂2019年共生产4000万件电子产品,该年还生产了A、B、C三种型号的电池,其数量分别为400万块、800万块、1600万块,这些电池只配装了该年生产的部分电子产品(每一件电子产品配一块电池),剩余电子产品所需电池由其他工厂供给.从2019年起,该工厂逐年扩大这三种类型的电池产量,2020年、2021年这两年,A型电池每年产量的增长率相同,B型电池每年产量的增长率比A型电池每年产量的增长率小1,C型电池每年产量的增长率是A型电池每年产量的增长率的一半.已知该工厂2021年生产的三种类型的电池恰好配装了该年生产的所有电子产品,且该年生产的电子产品的数量是2019年生产的电子产品的数量的3.3倍,求A型电池每年产量的增长率.
二.销售利润问题
8.某商店销售连衣裙,每条盈利40元,每天可以销售20条.商店决定降价销售,经调查,每降价1元,商店每天可多销售2条连衣裙.若想要商店每天盈利1200元,每条连衣裙应降价( )
A.5元 B.10元 C.20元 D.10元或20元
9.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元,若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(x+1)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(3+x)(4﹣0.5x)=15
10.某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元,要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加x株花苗,下面列出的方程中符合题意的是( )
A.(x+3)(5﹣0.5x)=20 B.(x﹣3)(5+0.5x)=20
C.(x﹣3)(5﹣0.5x)=20 D.(x+3)(5+0.5x)=20
11.某商店将进价为30元/件的文化衫以50元/件售出,每天可卖200件,在换季时期,预计单价每降低1元,每天可多卖10件,则销售单价定为多少元时,商店可获利3000元?设销售单价定为x元/件,可列方程为 .(方程不需化简)
12.一学校为了绿化校园环境,向某园林公司购买了一批树苗.园林公司规定:如果购买树苗不超过60棵,每棵售价为120元;如果购买树苗超过60棵,在一定范围内,每增加1棵,所出售的这批树苗每棵售价降低0.5元.若该校最终向园林公司支付树苗款8800元,设该校共购买了x棵树苗,则可列出方程 .
13.某商店经销的某种商品,每件成本为30元.经市场调研,售价为40元时,可销售200件;售价每增加2元,销售量将减少20件.如果这种商品全部销售完,该商店可盈利2250元,那么该商品每件售价多少元?
14.某商场将进价每件30元的衬衫以每件40元销售,平均每月可售出600件.为了增加盈利,商场采取涨价措施.若在一定范围内,衬衫的单价每涨1元,商场平均每月会少售出10件.为了实现平均每月10000元的销售利润,这种衬衫每件的价格应定为多少元?
15.某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
16.某商店销售甲、乙两种零食,甲零食每袋成本为5元,乙零食每袋成本为7元.甲零食现在的售价为10元,每天卖出30袋;售价每提高1元,每天少卖出2袋.乙零食现在的售价为14元,每天卖出6袋;售价每降低1元,每天多卖出4袋.假定甲、乙两种零食每天卖出的袋数的和不变(和为36袋),且售价均为整数.
(1)当甲零食的售价提高2元,则甲零食每天卖出 袋,乙零食的售价为 元;
(2)当甲零食的售价提高多少元时,销售这两种零食当天的总利润是268元?
17.列方程(组)解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
三.面积类问题
18.如图,学校课外小组的试验园地的形状是长30米宽15米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为392平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为( )
A.(30+2x)(15+x)=392 B.(30﹣2x)(15﹣x)=392
C.(30+x)(15+2x)=392 D.(30﹣x)(15﹣2x)=392
19.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.32x+2×20x﹣2x2=570 B.32x+2×20x=32×20﹣570
C.(32﹣2x)(20﹣x)=32×20﹣570 D.(32﹣2x)(20﹣x)=570
20.如图,靠墙建一个面积为100平方米的仓库,并在与墙平行的一边开一道宽1米的门,现有长28米的木板,设仓库宽为x米,根据题意,下面所列方程正确的是( )
A.x(28﹣2x)=100 B.x(28﹣2x+1)=100
C.x(28﹣x)=100 D.x(28﹣x+1)=100
21.小鹏的手中有一根长为40cm的铜丝,他想用这根铜丝分段围成一个面积为50cm2的如图所示的“日“字的矩形钢丝框,求该矩形钢丝框的长.设该矩形铜丝框的长为xcm,根据题意,可列方程为( )
A.x()=50 B.x()=50
C.x(40﹣3x)=50 D.x(40﹣2x)=50
22.某中学有一块长30m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则列方程为( )
A.(30﹣x)(20﹣x)=×20×30 B.(30﹣2x)(20﹣x)=×20×30
C.30x+2×20x=×20×30 D.(30﹣2x)(20﹣x)=×20×30
23.现有一块长方形绿地,它的短边长为20m,若将短边增大到与长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加300m2,设扩大后的正方形绿地边长为xm,下面所列方程正确的是( )
A.x(x﹣20)=300 B.x(x+20)=300
C.60(x+20)=300 D.60(x﹣20)=300
24.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )
A.(32+x)(20+x)=540 B.(32﹣x)(20﹣x)=540
C.(32+x)(20﹣x)=540 D.(32﹣x)(20+x)=540
25.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到点C后停止,点P也随之停止运动,若使△PBQ的面积为15cm2,则点P运动的时间是( )
A.2s B.3s C.4s D.5s
26.如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
27.如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
28.如图是中北居民小区某一休闲场所的平面示意图.图中阴影部分是草坪和健身器材安装区,空白部分是用做散步的道路.东西方向的一条主干道较宽,其余道路的宽度相等,主干道的宽度是其余道路的宽度的2倍.这块休闲场所南北长18m,东西宽16m.已知这休闲场地中草坪和健身器材安装区的面积为168m2,请问主干道的宽度为多少米?
29.有一农户用24m长的篱笆围成一面靠墙(墙长12m),大小相等且彼此相连的三个矩形鸡舍(如图).
(1)鸡场的面积能够达到32m2吗?若能,给出你的方案;若不能,请说明理由;
(2)鸡场的面积能够达到80m2吗?若能,给出你的方案;若不能,请说明理由.
30.如图,在一个长为40m,宽为26m的矩形花园中修建小道(图中阴影部分),其中AB=CD=EF=GH=xm,每段小道的两边缘平行,剩余的地方种植花草,要使种植花草的面积为864m2,求x的值.
四.比赛类问题
31.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛240场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )
A.x(x﹣1)=240 B.x(x﹣1)=240
C.x(x+1)=240 D.x(x+1)=240
32.2021年新年期间班上数学兴趣小组的同学互发微信祝贺,每两名同学都互相发一次.小明统计全组共互发了72次微信,设数学兴趣小组的人数为x,则可列方程为( )
A.x(x﹣1)=72 B.x(x﹣1)=2×72
C.x(x﹣1)=72 D.x(x+1)=72
33.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程为( )
A.x(x+1)=1892 B.x(x﹣1)=1892×2
C.x(x﹣1)=1892 D.2x(x+1)=1892
34.有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )
A.14 B.11 C.10 D.9
35.某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )
A.6 B.7 C.8 D.9
36.某校“研学”活动小组在一次野外实践时,发现一种植物的1个主干上长出x个枝干,每个枝干上再长出x个小分支.若在1个主干上的主干、枝干和小分支的数量之和是43个,则x等于( )
A.4 B.5 C.6 D.7
37.某中学初四学生毕业时,每个同学都给其他同学写了一份毕业留言,全班共写了纪念留言1640份,则全班共有学生( )名.
A.39 B.40 C.41 D.42
五.综合训练
38.某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )
A.800(1﹣x)2=968 B.800(1+x)2=968
C.968(1﹣x)2=800 D.968(1+x)2=800
39.随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是5000元,现在生产一吨药的成本是4050元.设生产成本的年平均下降率为x,下面所列方程正确的是( )
A.5000(1+x)2=4050 B.4050(1+x)2=5000
C.5000(1﹣x)2=4050 D.4050(1﹣x)2=5000
40.某种商品原价每件40元,经两次降价,现售价每件32.4元,则该种商品平均每次降价的百分率是 .
41.某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低1万元时,平均每周能多售出2辆.该4S店要想平均每周的销售利润为96万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
42.某商店将进价为10元的某种商品以14元售出,平均每天能售出220件.调查发现,这种商品的售价每上涨1元,其销售量就将减少20件.该商店计划通过提高商品售价减少销售量的办法增加利润.
(1)若物价部门规定此种商品的每件利润不能超过进价的80%,且商店想要获得平均每天1080元的利润,则这种商品的售价应定为多少?
(2)该商店平均每天盈利能否为1200元?
43.用一条长60cm的绳子怎样围成一个面积为200cm2的矩形?设矩形的一边为xcm,根据题意,可列方程为( )
A.x(30+x)=200 B.x(30﹣x)=200
C.x(x+60)=200 D.x(60﹣x)=200
44.如图,学校课外生物小组的试验园地是长20米,宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,则小道的宽为( )
A.5米 B.1米 C.2米 D.3米
45.如图,在宽为20m、长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551m2,则修建的路宽应为( )
A.1m B.1.5m C.2m D.2.5m
46.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
A.(x+1)(x+2)=18 B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18 D.x2+3x+16=0
47.某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为28米.
(1)这个车棚的长和宽分别应为多少米?
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?
参考答案
一.增长率问题
1.解:第一次降价后的价格为25(1﹣x),
第二次降价后的价格为25(1﹣x)×(1﹣x)=25×(1﹣x)2,
∴列的方程为25(1﹣x)2=16,
故选:B.
2.解:∵一月份的营业额为25万元,平均每月下降率为x,
∴二月份的营业额为25×(1﹣x)万元,
∴三月份营业额为25×(1﹣x)×(1﹣x),
∴可列方程为25(1﹣x)2=16,
故选:B.
3.解:这个给定的百分比为x,由题意得,
(1﹣x)(1+x)=84%,
∴x=0.4(负值舍去),
即这个给定的百分比为40%.
故选:C.
4.解:设平均每次降价的百分率为x,
依题意,得:(1﹣x)2=1﹣19%,
解得:x1=0.1=10%,x2=1.9(不合题意,舍去).
答:平均每次降价的百分率为10%.
故选:B.
5.解:设平均年增长率为x,
根据题意得:100(1+x)2=144,
整理得:(1+x)2=1.44,
开方得:1+x=±1.2,
解得:x=0.2=20%或x=﹣2.2(舍去),
则平均年增长率为20%,
∴该公司2020年盈利100(1+20%)=120(万元).
故答案为:120.
6.解:设平均每天票房的增长率为x,
根据题意得:1.92(1+x)2=2.61.
故答案为:1.92(1+x)2=2.61.
7.解:设A型电池每年产量的增长率为x,则B型电池每年产量的增长率为(x﹣1),C型电池每年产量的增长率为x,
依题意得:400(1+x)2+800(1+x﹣1)2+1600(1+x)2=4000×3.3,
整理得:2x2+3x﹣14=0,
解得:x1=2,x2=﹣(不合题意,舍去).
答:A型电池每年产量的增长率为2.
二.销售利润问题
8.解:设每条连衣裙降价x元,则每天售出(20+2x)条,
依题意,得:(40﹣x)(20+2x)=1200,
整理,得:x2﹣30x+200=0,
解得:x1=10,x2=20.
答:每条连衣裙应降价10元或20元.
故选:D.
9.解:设每盆应该多植x株,由题意得
(3+x)(4﹣0.5x)=15,
故选:D.
10.解:由题意可得,
(x+3)(5﹣0.5x)=20,
故选:A.
11.解:设销售单价定为x元/件,由题意可得:
(x﹣30)[200+10(50﹣x)]=3000,
故答案为:(x﹣30)[200+10(50﹣x)]=3000.
12.解:设该校共购买了x棵树苗,由题意得:
x[120﹣0.5(x﹣60)]=8800,
故答案为:x[120﹣0.5(x﹣60)]=8800.
13.解:设该商品每件售价x元.
根据题意,得(x﹣30)[200﹣10(x﹣40)]=2 250,
解这个方程,得x1=x2=45,
答:该商店每件售价45元.
14.解:设这种衬衫每件的价格应定为 x 元.
根据题意,得(x﹣30)[600﹣(x﹣40)×10]=10000.
解得 x1=50,x2=80.
答:这种衬衫每件的价格应定为 50 元或 80 元.
15.解:(1)由题意,可得当售价为22万元/辆时,平均每周的销售量是:×1+8=14,
则此时,平均每周的销售利润是:(22﹣15)×14=98(万元);
(2)设每辆汽车降价x万元,根据题意得:
(25﹣x﹣15)(8+2x)=90,
解得x1=1,x2=5,
当x=1时,销售数量为8+2×1=10(辆);
当x=5时,销售数量为8+2×5=18(辆),
为了尽快减少库存,则x=5,此时每辆汽车的售价为25﹣5=20(万元),
答:每辆汽车的售价为20万元.
16.解:(1)甲零食的售价提高2元,则甲零食每天卖出30﹣2×2=26(袋),
则乙销售了10袋,乙零食的售价为14﹣1=13(元).
故答案为:26,13;
(2)设甲零食的售价提高x元时,销售这两种零食当天的总利润是268元,由题意得,
(5+x)(30﹣2x)+(6+2x)(14﹣﹣7)=268,
∴3x2﹣31x+76=0,
解得x1=4,x2=,
∵售价均为整数,
∴x=4.
答:甲零食的售价提高4元时,销售这两种零食当天的总利润是268元.
17.解:设降低x元,超市每天可获得销售利润3640元,由题意得,
(38﹣x﹣22)(160+×120)=3640,
整理得x2﹣12x+27=0,
∴x=3或x=9.
∵要尽可能让顾客得到实惠,
∴x=9,
∴售价为38﹣9=29元.
答:水果的销售价为每千克29元时,超市每天可获得销售利润3640元.
三.面积类问题
18.解:设小道的宽为x米,则6个小矩形可合成长为(30﹣2x)米、宽为(15﹣x)米的大矩形,
依题意得:(30﹣2x)(15﹣x)=392.
故选:B.
19.解:设道路的宽为xm,则草坪的长为(32﹣2x)m,宽为(20﹣x)m,
根据题意得:(32﹣2x)(20﹣x)=570.
故选:D.
20.解:设仓库宽为x米,则长为(28﹣2x+1)米,
依题意,得:x(28﹣2x+1)=100.
故选:B.
21.解:设该矩形铜丝框的长为xcm,则钢丝框的宽为(),
由题意得,x()=50.
故选:A.
22.解:设花带的宽度为xm,则可列方程为(30﹣2x)(20﹣x)=×20×30,
故选:D.
23.解:设扩大后的正方形绿地边长为xm,根据题意得
x(x﹣20)=300.
故选:A.
24.解:设小路宽为x米,利用平移,得:(32﹣x)(20﹣x)=540.
故选:B.
25.解:设动点P,Q运动t秒后,能使△PBQ的面积为15cm2,
则BP为(8﹣t)cm,BQ为2tcm,由三角形的面积计算公式列方程得,
×(8﹣t)×2t=15,
解得t1=3,t2=5(当t=5时,BQ=10,不合题意,舍去).
∴动点P,Q运动3秒时,能使△PBQ的面积为15cm2.
故选:B.
26.解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1=,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为cm时,所得长方体盒子的侧面积为200cm2.
27.解:设宽为x m,则长为(16﹣2x)m.
由题意,得 x?(16﹣2x)=30,
解得 x1=3,x2=5.
当x=3时,16﹣2×3=10,
当x=5时,16﹣2×5=6.
答:围成矩形的长为10 m、宽为3 m,或长为6 m、宽为5m.
28.解:设主干道的宽度为2xm,则其余道路宽为xm,
依题意得:(16﹣4x)(18﹣4x)=168,
整理,得x1=1,x2=.
当x2=时,16﹣4x<0,不合题意,舍去.
当x=1米时,2x=2米.
答:主干道的宽度为2米.
29.解:(1)能,设垂直于墙的一边长x,则(24﹣4x)?x=32,
整理得x2﹣6x+8=0
解得x1=4,x2=2(24﹣4x=16>12,舍)垂直于墙的一边长为4m,平行于墙的一边长为8m.
(2)不能.解方程:(24﹣4x)?x=80,
整理得x2﹣6x+20=0,
解得此方程无实数根,所以不能.
30.解:种植花草部分可合成长为(40﹣2x)m,宽为(26﹣x)m的矩形,
依题意得:(40﹣2x)(26﹣x)=864,
整理得:x2﹣46x+88=0,
解得:x1=2,x2=44(不合题意,舍去).
故答案为:2.
四.比赛类问题
31.解:依题意得:x(x﹣1)=240.
故选:A.
32.解:由题意可得,
x(x﹣1)=72,
故选:A.
33.解:∵全班有x名同学,
∴每名同学要送出(x﹣1)张;
又∵是互送照片,
∴总共送的张数应该是x(x﹣1)=1892.
故选:C.
34.解:设每轮传染中平均一个人传染了x个人,依题意得1+x+x(1+x)=144,
即(1+x)2=144,
解方程得x1=11,x2=﹣13(舍去),
故选:B.
35.解:设参加此次比赛的球队数为x队,根据题意得:
x(x﹣1)=36,
化简,得x2﹣x﹣72=0,
解得x1=9,x2=﹣8(舍去),
∴参加此次比赛的球队数是9队.
故选:D.
36.解:依题意,得:1+x+x2=43,
整理,得:x2+x﹣42=0,
解得:x1=6,x2=﹣7(不合题意,舍去).
故选:C.
37.解:设全班共有学生x名,则每名学生需写(x﹣1)份毕业留言,
依题意得:x(x﹣1)=1640,
解得:x1=41,x2=﹣40(不合题意,舍去).
故选:C.
五.综合训练:
38.解:依题意得:800(1+x)2=968.
故选:B.
39.解:设这种药品成本的年平均下降率是x,根据题意得:
5000(1﹣x)2=4050,
故选:C.
40.解:设降价百分率为x,
列方程:40(1﹣x)2=32.4.
解得x1=0.1,x2=1.9(不合题意舍去).
故答案为:10%.
41.解:设每辆汽车的定价应为x元,则每辆的销售利润为(x﹣15)万元,平均每周的销售量为8+2(25﹣x)=(58﹣2x)辆,
依题意得:(x﹣15)(58﹣2x)=96,
整理得:x2﹣44x+483=0,
解得:x1=21,x2=23.
又∵为使成本尽可能的低,
∴x=23.
答:每辆汽车的定价应为23万元.
42.解:(1)设这种商品的售价应定为x元,则每件的销售利润为(x﹣10)元,日销售量为220﹣20(x﹣14)=(500﹣20x)件,
依题意得:(x﹣10)(500﹣20x)=1080,
整理得:x2﹣35x+304=0,
解得:x1=16,x2=19.
∵10×(1+80%)=18(元),16<18<19,
∴x=16.
答:这种商品的售价应定为16元.
(2)设这种商品的售价应定为y元,则每件的销售利润为(y﹣10)元,日销售量为220﹣20(y﹣14)=(500﹣20y)件,
依题意得:(y﹣10)(500﹣20y)=1200,
整理得:y2﹣35y+310=0.
∵△=(﹣35)2﹣4×1×310=﹣15<0,
∴该方程无实数根,
∴该商店平均每天盈利不能为1200元.
43.解:设矩形的一边为x米,
∵长方形的周长为60cm,
∴矩形的另一边=(30﹣x)(cm),
得x(30﹣x)=200.
故选:B.
44.解:设该小道的宽为x米,依题意得
(20﹣2x)(15﹣x)=252,
整理得x2﹣25x+24=0,
即:(x﹣24)(x﹣1)=0,
解得x1=24(舍去),x2=1.
即:该小道的宽为1米.
故选:B.
45.解:设修建的路宽应为x米
根据等量关系列方程得:30×20﹣(20x+30x﹣x2)=551,
解得:x1=49(不合题意,舍去),x2=1.
故选:A.
46.解:设原正方形的边长为xm,依题意有
(x﹣1)(x﹣2)=18,
故选:C.
47.解:(1)设平行于墙的边长为x米,则垂直于墙的边长为米,
依题意得:x?=80,
整理得:x2﹣28x+160=0,
解得:x1=8,x2=20.
又∵这堵墙的长度为12米,
∴x=8,
∴=10.
答:这个车棚的长为10米,宽为8米.
(2)设小路的宽度是m米,则停放自行车的区域可合成长为(10﹣m)米,宽为(8﹣2m)米的长方形,
依题意得:(10﹣m)(8﹣2m)=54,
整理得:m2﹣14m+13=0,
解得:m1=1,m2=13.
当m=1时,10﹣m=9,8﹣2m=6,符合题意;
当m=13时,10﹣m=﹣3,不合题意,舍去.
答:小路的宽度是1米.
一.增长率问题
1.一种药品原价为25元,经过两次降价后每盒16元,设两次降价的百分率都同为x,则x满足方程( )
A.25(1﹣2x2)=16 B.25(1﹣x)2=16
C.16(1+2x2)=25 D.16(1+x)2=25
2.某超市一月份的营业额为25万元,三月份时因新冠疫情下降到16万元,若平均每月下降率为x,则由题意列方程应为( )
A.25(1+x)2=16 B.25(1﹣x)2=16
C.16(1+x)2=25 D.25[1+(1﹣x)+(1﹣x)2]=16
3.双十一来临前,某商场将一件衬衫的价格以一个给定的百分比提升,双十一那天商场又按照新的价格以相同的百分比降低了这件衬衫的价格,最终,衬衫的价格为原价的84%,则这个给定的百分比为( )
A.16% B.36% C.40% D.50%
4.为响应中央“房住不炒”的基本政策,某房企连续降价两次后的平均价格比降价之前减少了19%,则平均每次降价的百分率为( )
A.9.5% B.10% C.10.5% D.11%
5.某商贸公司2019年盈利100万元,2021年盈利144万元,且2019年到2021年每年盈利的增长率相同,则该公司2020年盈利 万元.
6.电影《中国机长》首映当日票房已经达到1.92亿元,2天后当日票房达到2.61亿元,设平均每天票房的增长率为x,则可列方程为 .
7.某工厂2019年共生产4000万件电子产品,该年还生产了A、B、C三种型号的电池,其数量分别为400万块、800万块、1600万块,这些电池只配装了该年生产的部分电子产品(每一件电子产品配一块电池),剩余电子产品所需电池由其他工厂供给.从2019年起,该工厂逐年扩大这三种类型的电池产量,2020年、2021年这两年,A型电池每年产量的增长率相同,B型电池每年产量的增长率比A型电池每年产量的增长率小1,C型电池每年产量的增长率是A型电池每年产量的增长率的一半.已知该工厂2021年生产的三种类型的电池恰好配装了该年生产的所有电子产品,且该年生产的电子产品的数量是2019年生产的电子产品的数量的3.3倍,求A型电池每年产量的增长率.
二.销售利润问题
8.某商店销售连衣裙,每条盈利40元,每天可以销售20条.商店决定降价销售,经调查,每降价1元,商店每天可多销售2条连衣裙.若想要商店每天盈利1200元,每条连衣裙应降价( )
A.5元 B.10元 C.20元 D.10元或20元
9.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元,若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(x+1)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(3+x)(4﹣0.5x)=15
10.某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元,要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加x株花苗,下面列出的方程中符合题意的是( )
A.(x+3)(5﹣0.5x)=20 B.(x﹣3)(5+0.5x)=20
C.(x﹣3)(5﹣0.5x)=20 D.(x+3)(5+0.5x)=20
11.某商店将进价为30元/件的文化衫以50元/件售出,每天可卖200件,在换季时期,预计单价每降低1元,每天可多卖10件,则销售单价定为多少元时,商店可获利3000元?设销售单价定为x元/件,可列方程为 .(方程不需化简)
12.一学校为了绿化校园环境,向某园林公司购买了一批树苗.园林公司规定:如果购买树苗不超过60棵,每棵售价为120元;如果购买树苗超过60棵,在一定范围内,每增加1棵,所出售的这批树苗每棵售价降低0.5元.若该校最终向园林公司支付树苗款8800元,设该校共购买了x棵树苗,则可列出方程 .
13.某商店经销的某种商品,每件成本为30元.经市场调研,售价为40元时,可销售200件;售价每增加2元,销售量将减少20件.如果这种商品全部销售完,该商店可盈利2250元,那么该商品每件售价多少元?
14.某商场将进价每件30元的衬衫以每件40元销售,平均每月可售出600件.为了增加盈利,商场采取涨价措施.若在一定范围内,衬衫的单价每涨1元,商场平均每月会少售出10件.为了实现平均每月10000元的销售利润,这种衬衫每件的价格应定为多少元?
15.某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
16.某商店销售甲、乙两种零食,甲零食每袋成本为5元,乙零食每袋成本为7元.甲零食现在的售价为10元,每天卖出30袋;售价每提高1元,每天少卖出2袋.乙零食现在的售价为14元,每天卖出6袋;售价每降低1元,每天多卖出4袋.假定甲、乙两种零食每天卖出的袋数的和不变(和为36袋),且售价均为整数.
(1)当甲零食的售价提高2元,则甲零食每天卖出 袋,乙零食的售价为 元;
(2)当甲零食的售价提高多少元时,销售这两种零食当天的总利润是268元?
17.列方程(组)解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
三.面积类问题
18.如图,学校课外小组的试验园地的形状是长30米宽15米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为392平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为( )
A.(30+2x)(15+x)=392 B.(30﹣2x)(15﹣x)=392
C.(30+x)(15+2x)=392 D.(30﹣x)(15﹣2x)=392
19.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.32x+2×20x﹣2x2=570 B.32x+2×20x=32×20﹣570
C.(32﹣2x)(20﹣x)=32×20﹣570 D.(32﹣2x)(20﹣x)=570
20.如图,靠墙建一个面积为100平方米的仓库,并在与墙平行的一边开一道宽1米的门,现有长28米的木板,设仓库宽为x米,根据题意,下面所列方程正确的是( )
A.x(28﹣2x)=100 B.x(28﹣2x+1)=100
C.x(28﹣x)=100 D.x(28﹣x+1)=100
21.小鹏的手中有一根长为40cm的铜丝,他想用这根铜丝分段围成一个面积为50cm2的如图所示的“日“字的矩形钢丝框,求该矩形钢丝框的长.设该矩形铜丝框的长为xcm,根据题意,可列方程为( )
A.x()=50 B.x()=50
C.x(40﹣3x)=50 D.x(40﹣2x)=50
22.某中学有一块长30m,宽20m的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为xm,则列方程为( )
A.(30﹣x)(20﹣x)=×20×30 B.(30﹣2x)(20﹣x)=×20×30
C.30x+2×20x=×20×30 D.(30﹣2x)(20﹣x)=×20×30
23.现有一块长方形绿地,它的短边长为20m,若将短边增大到与长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加300m2,设扩大后的正方形绿地边长为xm,下面所列方程正确的是( )
A.x(x﹣20)=300 B.x(x+20)=300
C.60(x+20)=300 D.60(x﹣20)=300
24.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )
A.(32+x)(20+x)=540 B.(32﹣x)(20﹣x)=540
C.(32+x)(20﹣x)=540 D.(32﹣x)(20+x)=540
25.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到点C后停止,点P也随之停止运动,若使△PBQ的面积为15cm2,则点P运动的时间是( )
A.2s B.3s C.4s D.5s
26.如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?
27.如图,学校打算用16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图),面积是30m2.求生物园的长和宽.
28.如图是中北居民小区某一休闲场所的平面示意图.图中阴影部分是草坪和健身器材安装区,空白部分是用做散步的道路.东西方向的一条主干道较宽,其余道路的宽度相等,主干道的宽度是其余道路的宽度的2倍.这块休闲场所南北长18m,东西宽16m.已知这休闲场地中草坪和健身器材安装区的面积为168m2,请问主干道的宽度为多少米?
29.有一农户用24m长的篱笆围成一面靠墙(墙长12m),大小相等且彼此相连的三个矩形鸡舍(如图).
(1)鸡场的面积能够达到32m2吗?若能,给出你的方案;若不能,请说明理由;
(2)鸡场的面积能够达到80m2吗?若能,给出你的方案;若不能,请说明理由.
30.如图,在一个长为40m,宽为26m的矩形花园中修建小道(图中阴影部分),其中AB=CD=EF=GH=xm,每段小道的两边缘平行,剩余的地方种植花草,要使种植花草的面积为864m2,求x的值.
四.比赛类问题
31.参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛240场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )
A.x(x﹣1)=240 B.x(x﹣1)=240
C.x(x+1)=240 D.x(x+1)=240
32.2021年新年期间班上数学兴趣小组的同学互发微信祝贺,每两名同学都互相发一次.小明统计全组共互发了72次微信,设数学兴趣小组的人数为x,则可列方程为( )
A.x(x﹣1)=72 B.x(x﹣1)=2×72
C.x(x﹣1)=72 D.x(x+1)=72
33.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程为( )
A.x(x+1)=1892 B.x(x﹣1)=1892×2
C.x(x﹣1)=1892 D.2x(x+1)=1892
34.有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )
A.14 B.11 C.10 D.9
35.某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )
A.6 B.7 C.8 D.9
36.某校“研学”活动小组在一次野外实践时,发现一种植物的1个主干上长出x个枝干,每个枝干上再长出x个小分支.若在1个主干上的主干、枝干和小分支的数量之和是43个,则x等于( )
A.4 B.5 C.6 D.7
37.某中学初四学生毕业时,每个同学都给其他同学写了一份毕业留言,全班共写了纪念留言1640份,则全班共有学生( )名.
A.39 B.40 C.41 D.42
五.综合训练
38.某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )
A.800(1﹣x)2=968 B.800(1+x)2=968
C.968(1﹣x)2=800 D.968(1+x)2=800
39.随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是5000元,现在生产一吨药的成本是4050元.设生产成本的年平均下降率为x,下面所列方程正确的是( )
A.5000(1+x)2=4050 B.4050(1+x)2=5000
C.5000(1﹣x)2=4050 D.4050(1﹣x)2=5000
40.某种商品原价每件40元,经两次降价,现售价每件32.4元,则该种商品平均每次降价的百分率是 .
41.某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低1万元时,平均每周能多售出2辆.该4S店要想平均每周的销售利润为96万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
42.某商店将进价为10元的某种商品以14元售出,平均每天能售出220件.调查发现,这种商品的售价每上涨1元,其销售量就将减少20件.该商店计划通过提高商品售价减少销售量的办法增加利润.
(1)若物价部门规定此种商品的每件利润不能超过进价的80%,且商店想要获得平均每天1080元的利润,则这种商品的售价应定为多少?
(2)该商店平均每天盈利能否为1200元?
43.用一条长60cm的绳子怎样围成一个面积为200cm2的矩形?设矩形的一边为xcm,根据题意,可列方程为( )
A.x(30+x)=200 B.x(30﹣x)=200
C.x(x+60)=200 D.x(60﹣x)=200
44.如图,学校课外生物小组的试验园地是长20米,宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,则小道的宽为( )
A.5米 B.1米 C.2米 D.3米
45.如图,在宽为20m、长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551m2,则修建的路宽应为( )
A.1m B.1.5m C.2m D.2.5m
46.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
A.(x+1)(x+2)=18 B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18 D.x2+3x+16=0
47.某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为28米.
(1)这个车棚的长和宽分别应为多少米?
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽度是多少米?
参考答案
一.增长率问题
1.解:第一次降价后的价格为25(1﹣x),
第二次降价后的价格为25(1﹣x)×(1﹣x)=25×(1﹣x)2,
∴列的方程为25(1﹣x)2=16,
故选:B.
2.解:∵一月份的营业额为25万元,平均每月下降率为x,
∴二月份的营业额为25×(1﹣x)万元,
∴三月份营业额为25×(1﹣x)×(1﹣x),
∴可列方程为25(1﹣x)2=16,
故选:B.
3.解:这个给定的百分比为x,由题意得,
(1﹣x)(1+x)=84%,
∴x=0.4(负值舍去),
即这个给定的百分比为40%.
故选:C.
4.解:设平均每次降价的百分率为x,
依题意,得:(1﹣x)2=1﹣19%,
解得:x1=0.1=10%,x2=1.9(不合题意,舍去).
答:平均每次降价的百分率为10%.
故选:B.
5.解:设平均年增长率为x,
根据题意得:100(1+x)2=144,
整理得:(1+x)2=1.44,
开方得:1+x=±1.2,
解得:x=0.2=20%或x=﹣2.2(舍去),
则平均年增长率为20%,
∴该公司2020年盈利100(1+20%)=120(万元).
故答案为:120.
6.解:设平均每天票房的增长率为x,
根据题意得:1.92(1+x)2=2.61.
故答案为:1.92(1+x)2=2.61.
7.解:设A型电池每年产量的增长率为x,则B型电池每年产量的增长率为(x﹣1),C型电池每年产量的增长率为x,
依题意得:400(1+x)2+800(1+x﹣1)2+1600(1+x)2=4000×3.3,
整理得:2x2+3x﹣14=0,
解得:x1=2,x2=﹣(不合题意,舍去).
答:A型电池每年产量的增长率为2.
二.销售利润问题
8.解:设每条连衣裙降价x元,则每天售出(20+2x)条,
依题意,得:(40﹣x)(20+2x)=1200,
整理,得:x2﹣30x+200=0,
解得:x1=10,x2=20.
答:每条连衣裙应降价10元或20元.
故选:D.
9.解:设每盆应该多植x株,由题意得
(3+x)(4﹣0.5x)=15,
故选:D.
10.解:由题意可得,
(x+3)(5﹣0.5x)=20,
故选:A.
11.解:设销售单价定为x元/件,由题意可得:
(x﹣30)[200+10(50﹣x)]=3000,
故答案为:(x﹣30)[200+10(50﹣x)]=3000.
12.解:设该校共购买了x棵树苗,由题意得:
x[120﹣0.5(x﹣60)]=8800,
故答案为:x[120﹣0.5(x﹣60)]=8800.
13.解:设该商品每件售价x元.
根据题意,得(x﹣30)[200﹣10(x﹣40)]=2 250,
解这个方程,得x1=x2=45,
答:该商店每件售价45元.
14.解:设这种衬衫每件的价格应定为 x 元.
根据题意,得(x﹣30)[600﹣(x﹣40)×10]=10000.
解得 x1=50,x2=80.
答:这种衬衫每件的价格应定为 50 元或 80 元.
15.解:(1)由题意,可得当售价为22万元/辆时,平均每周的销售量是:×1+8=14,
则此时,平均每周的销售利润是:(22﹣15)×14=98(万元);
(2)设每辆汽车降价x万元,根据题意得:
(25﹣x﹣15)(8+2x)=90,
解得x1=1,x2=5,
当x=1时,销售数量为8+2×1=10(辆);
当x=5时,销售数量为8+2×5=18(辆),
为了尽快减少库存,则x=5,此时每辆汽车的售价为25﹣5=20(万元),
答:每辆汽车的售价为20万元.
16.解:(1)甲零食的售价提高2元,则甲零食每天卖出30﹣2×2=26(袋),
则乙销售了10袋,乙零食的售价为14﹣1=13(元).
故答案为:26,13;
(2)设甲零食的售价提高x元时,销售这两种零食当天的总利润是268元,由题意得,
(5+x)(30﹣2x)+(6+2x)(14﹣﹣7)=268,
∴3x2﹣31x+76=0,
解得x1=4,x2=,
∵售价均为整数,
∴x=4.
答:甲零食的售价提高4元时,销售这两种零食当天的总利润是268元.
17.解:设降低x元,超市每天可获得销售利润3640元,由题意得,
(38﹣x﹣22)(160+×120)=3640,
整理得x2﹣12x+27=0,
∴x=3或x=9.
∵要尽可能让顾客得到实惠,
∴x=9,
∴售价为38﹣9=29元.
答:水果的销售价为每千克29元时,超市每天可获得销售利润3640元.
三.面积类问题
18.解:设小道的宽为x米,则6个小矩形可合成长为(30﹣2x)米、宽为(15﹣x)米的大矩形,
依题意得:(30﹣2x)(15﹣x)=392.
故选:B.
19.解:设道路的宽为xm,则草坪的长为(32﹣2x)m,宽为(20﹣x)m,
根据题意得:(32﹣2x)(20﹣x)=570.
故选:D.
20.解:设仓库宽为x米,则长为(28﹣2x+1)米,
依题意,得:x(28﹣2x+1)=100.
故选:B.
21.解:设该矩形铜丝框的长为xcm,则钢丝框的宽为(),
由题意得,x()=50.
故选:A.
22.解:设花带的宽度为xm,则可列方程为(30﹣2x)(20﹣x)=×20×30,
故选:D.
23.解:设扩大后的正方形绿地边长为xm,根据题意得
x(x﹣20)=300.
故选:A.
24.解:设小路宽为x米,利用平移,得:(32﹣x)(20﹣x)=540.
故选:B.
25.解:设动点P,Q运动t秒后,能使△PBQ的面积为15cm2,
则BP为(8﹣t)cm,BQ为2tcm,由三角形的面积计算公式列方程得,
×(8﹣t)×2t=15,
解得t1=3,t2=5(当t=5时,BQ=10,不合题意,舍去).
∴动点P,Q运动3秒时,能使△PBQ的面积为15cm2.
故选:B.
26.解:设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1=,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为cm时,所得长方体盒子的侧面积为200cm2.
27.解:设宽为x m,则长为(16﹣2x)m.
由题意,得 x?(16﹣2x)=30,
解得 x1=3,x2=5.
当x=3时,16﹣2×3=10,
当x=5时,16﹣2×5=6.
答:围成矩形的长为10 m、宽为3 m,或长为6 m、宽为5m.
28.解:设主干道的宽度为2xm,则其余道路宽为xm,
依题意得:(16﹣4x)(18﹣4x)=168,
整理,得x1=1,x2=.
当x2=时,16﹣4x<0,不合题意,舍去.
当x=1米时,2x=2米.
答:主干道的宽度为2米.
29.解:(1)能,设垂直于墙的一边长x,则(24﹣4x)?x=32,
整理得x2﹣6x+8=0
解得x1=4,x2=2(24﹣4x=16>12,舍)垂直于墙的一边长为4m,平行于墙的一边长为8m.
(2)不能.解方程:(24﹣4x)?x=80,
整理得x2﹣6x+20=0,
解得此方程无实数根,所以不能.
30.解:种植花草部分可合成长为(40﹣2x)m,宽为(26﹣x)m的矩形,
依题意得:(40﹣2x)(26﹣x)=864,
整理得:x2﹣46x+88=0,
解得:x1=2,x2=44(不合题意,舍去).
故答案为:2.
四.比赛类问题
31.解:依题意得:x(x﹣1)=240.
故选:A.
32.解:由题意可得,
x(x﹣1)=72,
故选:A.
33.解:∵全班有x名同学,
∴每名同学要送出(x﹣1)张;
又∵是互送照片,
∴总共送的张数应该是x(x﹣1)=1892.
故选:C.
34.解:设每轮传染中平均一个人传染了x个人,依题意得1+x+x(1+x)=144,
即(1+x)2=144,
解方程得x1=11,x2=﹣13(舍去),
故选:B.
35.解:设参加此次比赛的球队数为x队,根据题意得:
x(x﹣1)=36,
化简,得x2﹣x﹣72=0,
解得x1=9,x2=﹣8(舍去),
∴参加此次比赛的球队数是9队.
故选:D.
36.解:依题意,得:1+x+x2=43,
整理,得:x2+x﹣42=0,
解得:x1=6,x2=﹣7(不合题意,舍去).
故选:C.
37.解:设全班共有学生x名,则每名学生需写(x﹣1)份毕业留言,
依题意得:x(x﹣1)=1640,
解得:x1=41,x2=﹣40(不合题意,舍去).
故选:C.
五.综合训练:
38.解:依题意得:800(1+x)2=968.
故选:B.
39.解:设这种药品成本的年平均下降率是x,根据题意得:
5000(1﹣x)2=4050,
故选:C.
40.解:设降价百分率为x,
列方程:40(1﹣x)2=32.4.
解得x1=0.1,x2=1.9(不合题意舍去).
故答案为:10%.
41.解:设每辆汽车的定价应为x元,则每辆的销售利润为(x﹣15)万元,平均每周的销售量为8+2(25﹣x)=(58﹣2x)辆,
依题意得:(x﹣15)(58﹣2x)=96,
整理得:x2﹣44x+483=0,
解得:x1=21,x2=23.
又∵为使成本尽可能的低,
∴x=23.
答:每辆汽车的定价应为23万元.
42.解:(1)设这种商品的售价应定为x元,则每件的销售利润为(x﹣10)元,日销售量为220﹣20(x﹣14)=(500﹣20x)件,
依题意得:(x﹣10)(500﹣20x)=1080,
整理得:x2﹣35x+304=0,
解得:x1=16,x2=19.
∵10×(1+80%)=18(元),16<18<19,
∴x=16.
答:这种商品的售价应定为16元.
(2)设这种商品的售价应定为y元,则每件的销售利润为(y﹣10)元,日销售量为220﹣20(y﹣14)=(500﹣20y)件,
依题意得:(y﹣10)(500﹣20y)=1200,
整理得:y2﹣35y+310=0.
∵△=(﹣35)2﹣4×1×310=﹣15<0,
∴该方程无实数根,
∴该商店平均每天盈利不能为1200元.
43.解:设矩形的一边为x米,
∵长方形的周长为60cm,
∴矩形的另一边=(30﹣x)(cm),
得x(30﹣x)=200.
故选:B.
44.解:设该小道的宽为x米,依题意得
(20﹣2x)(15﹣x)=252,
整理得x2﹣25x+24=0,
即:(x﹣24)(x﹣1)=0,
解得x1=24(舍去),x2=1.
即:该小道的宽为1米.
故选:B.
45.解:设修建的路宽应为x米
根据等量关系列方程得:30×20﹣(20x+30x﹣x2)=551,
解得:x1=49(不合题意,舍去),x2=1.
故选:A.
46.解:设原正方形的边长为xm,依题意有
(x﹣1)(x﹣2)=18,
故选:C.
47.解:(1)设平行于墙的边长为x米,则垂直于墙的边长为米,
依题意得:x?=80,
整理得:x2﹣28x+160=0,
解得:x1=8,x2=20.
又∵这堵墙的长度为12米,
∴x=8,
∴=10.
答:这个车棚的长为10米,宽为8米.
(2)设小路的宽度是m米,则停放自行车的区域可合成长为(10﹣m)米,宽为(8﹣2m)米的长方形,
依题意得:(10﹣m)(8﹣2m)=54,
整理得:m2﹣14m+13=0,
解得:m1=1,m2=13.
当m=1时,10﹣m=9,8﹣2m=6,符合题意;
当m=13时,10﹣m=﹣3,不合题意,舍去.
答:小路的宽度是1米.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
