云南省会泽县茚旺高级中学2012届高三上学期期中考试数学(文)试题
文档属性
| 名称 | 云南省会泽县茚旺高级中学2012届高三上学期期中考试数学(文)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 507.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-05 00:00:00 | ||
图片预览





文档简介
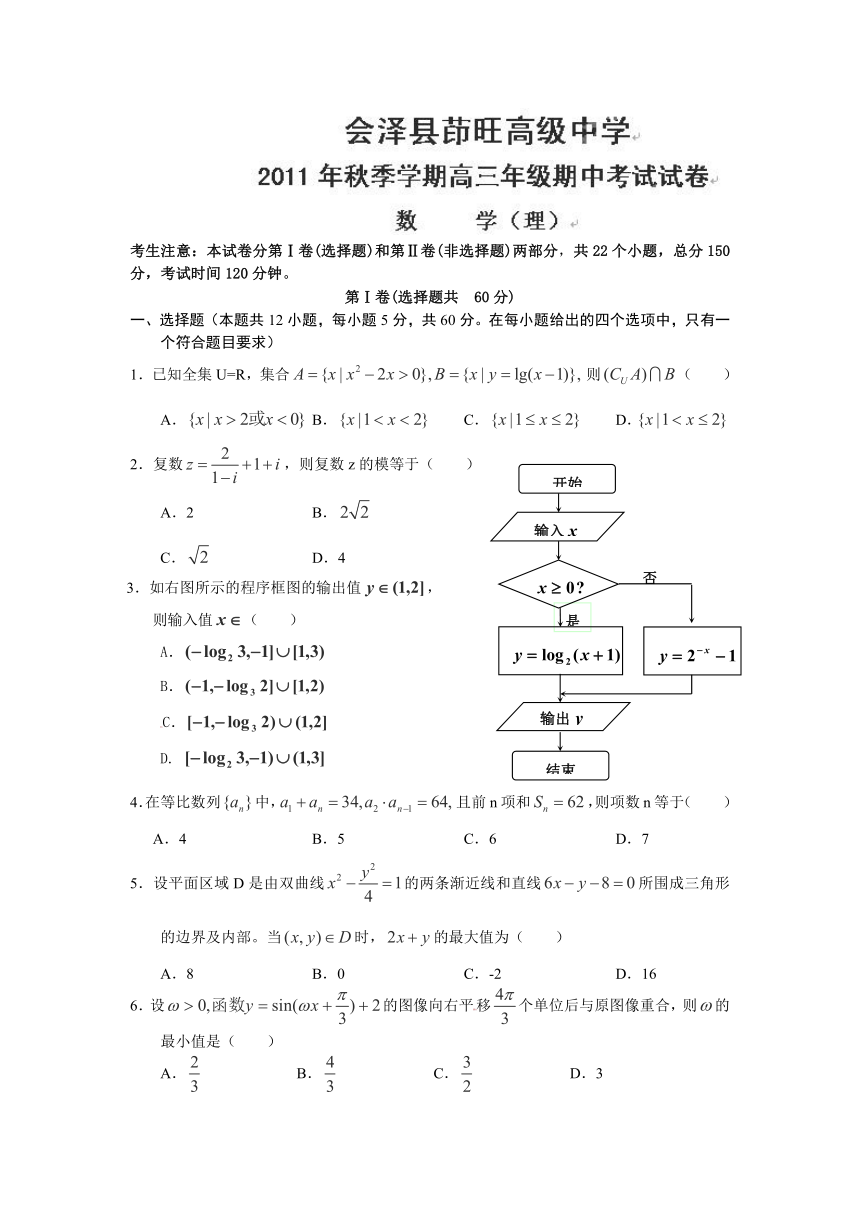
考生注意:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22个小题,总分150分,考试时间120分钟。
第Ⅰ卷(选择题共 60分)
一、选择题(本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个符合题目要求)
1.已知全集U=R,集合则( )
A. B. C. D.
2.复数,则复数z的模等于( )
A.2 B.
C. D.4
3.如右图所示的程序框图的输出值,
则输入值( )
A.
B.
C.
D.
4.在等比数列中,且前n项和,则项数n等于( )
A.4 B.5 C.6 D.7
5.设平面区域D是由双曲线的两条渐近线和直线所围成三角形的边界及内部。当时,的最大值为( )
A.8 B.0 C.-2 D.16
6.设的图像向右平移个单位后与原图像重合,则的最小值是( )
A. B. C. D.3
7.已知是双曲线的左、右焦点,过F1且垂直于x轴的直线与双曲线的左支交于A、B两点△ABF2是正三角形,那么双曲线的离心率为 ( )
A. B. C. 2 D.3
8.已知向量,的夹角为60°,||=||=2,若=2+,则△ABC为( )
A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
9.一个几何体的三视图如图所示,则这个几何体的体积是( )
A. B.1
C. D.2
10.设,则函数
在区间[1,2]上有零点的概率是( )
A. B.
C. D.
11.下列关于函数判断正确的是( )
①的解集是;
②是极小值,是极大值;
③没有最小值,也没有最大值.
A.①③ B.①②③ C.② D.①②
12.定义域为R的函数对任意x都有,且其导函数,则当,有 ( )
A. B.
C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题(本题共4个小题。每小题5分,共20分,将答案填在答题卡的相应位置)
13.若,若的最大值为,则的值是____________
14.如右上图,古希腊数学家把数1,3,6,10,15,21,…叫做
三角数,它们有一定的规律性,第30个三角数与第28个三角数
的差为 。
15.的展开式中各项系数和是128,则展开式中的系数是 。(用数字作答)
16.在△ABC中,A=120°,b=1,面积为,则= 。
三、解答题(本题共6小题,总分70分。解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)已知数列的前项和,
(1)求和;
(2)记,求数列的前项和.
18. (本题满分12分)已知向量.
(1)当时,求的值;
(2)设函数,已知在△ABC中,内角A、B、C的对边分别为,若,求 ()的取值范围.
19.(本题满分12分)第26届世界大学生夏季运动会将于2011年11月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用表示所选志愿者中能担任“礼仪小姐”的人数,试写出的分布列,并求的数学期望。
20.(本题满分12分)
如图,是圆的直径,点在圆上,,交于点,平面,,.
(1)证明:;
(2)求平面与平面所成的锐二面角的余弦值.
21.(本小题满分12分)
已知点是椭圆的右焦点,点、分别是轴、轴上的动点,且满足.若点满足.
(1)求点的轨迹的方程;
(2)设过点任作一直线与点的轨迹交于、两点,直线、与直线 分别交于点、(为坐标原点),试判断是否为定值?若是,求出这个定值;若不是,请说明理由.
22.(本小题满分12分)已知函数 .
(1)讨论函数的单调性;
(2)当时,恒成立,求实数的取值范围;
(3)证明:.
高三数学(理工类)参考答案
一、选择题:
1.D 2.B 3.D 4.B 5.A 6.C 7.B 8.C 9.A 10.C 11.D 12.A
二、填空题:
13.1 14.59 15.—35 16.2
三、解答题:
(Ⅱ) 设数列的前项和为,
时,, -------------------6分
时
故:数列的前项和 ---------------------10分
18.解:(1) …………2分
…………6分
(2)+
由正弦定理得 …………………9分
,,
所以 --------------------12分
(2)依题意,的取值为. ………………………7分
, ,
, . …………………………9分
因此,的分布列如下:
………………10分
. …………………………12分
20.解:(法一)(1)平面平面, .……………1分
又,
平面
而平面
. ………………………………………3分
是圆的直径,.
又,
.
平面,,
平面.
与都是等腰直角三角形.
.
,即(也可由勾股定理证得).………………5分
, 平面.
而平面,
. ………………………………………………………………6分
(法二)(1)同法一,得. ……………………3分
如图,以为坐标原点,垂直于..所在的直线为轴建立空间直角坐标系.
由已知条件得,
. ………4分
由,
得, . ……………6分
(2)由(1)知.
设平面的法向量为,
由 得,
令得,, ………………9分
由已知平面,所以取面的法向量为,
设平面与平面所成的锐二面角为,
则, …………………………11分
平面与平面所成的锐二面角的余弦值为. ……………………12分
(2)(法一)设直线的方程为,.,
则,. ………………………………5分
由,得, 同理得.…………………………7分
,,则. ………8分
由,得,. ……………………9分
则. …………………………11分
因此,的值是定值,且定值为. ………………………12分
(法二)①当时, .,则, .
由 得点的坐标为,则.
由 得点的坐标为,则.
. ………………………………………6分
22解:(1)的定义域为(0,+∞),
当时,>0,故在(0,+∞)单调递增;
当时,<0,故在(0,+∞)单调递减;……………2分
当-1<<0时,令=0,解得.
则当时,>0;时,<0.
故在单调递增,在单调递减. …………4分
(2)因为,所以
当时,恒成立
令,则, ……………6分
因为,由得,
且当时,;当时,.
所以在上递增,在上递减.所以,
故 ……………………8分
输出
是
开始
结束
输入
否
A
B
C
E
F
M
O
x
y
z
A
B
C
E
F
M
O
第Ⅰ卷(选择题共 60分)
一、选择题(本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个符合题目要求)
1.已知全集U=R,集合则( )
A. B. C. D.
2.复数,则复数z的模等于( )
A.2 B.
C. D.4
3.如右图所示的程序框图的输出值,
则输入值( )
A.
B.
C.
D.
4.在等比数列中,且前n项和,则项数n等于( )
A.4 B.5 C.6 D.7
5.设平面区域D是由双曲线的两条渐近线和直线所围成三角形的边界及内部。当时,的最大值为( )
A.8 B.0 C.-2 D.16
6.设的图像向右平移个单位后与原图像重合,则的最小值是( )
A. B. C. D.3
7.已知是双曲线的左、右焦点,过F1且垂直于x轴的直线与双曲线的左支交于A、B两点△ABF2是正三角形,那么双曲线的离心率为 ( )
A. B. C. 2 D.3
8.已知向量,的夹角为60°,||=||=2,若=2+,则△ABC为( )
A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
9.一个几何体的三视图如图所示,则这个几何体的体积是( )
A. B.1
C. D.2
10.设,则函数
在区间[1,2]上有零点的概率是( )
A. B.
C. D.
11.下列关于函数判断正确的是( )
①的解集是;
②是极小值,是极大值;
③没有最小值,也没有最大值.
A.①③ B.①②③ C.② D.①②
12.定义域为R的函数对任意x都有,且其导函数,则当,有 ( )
A. B.
C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题(本题共4个小题。每小题5分,共20分,将答案填在答题卡的相应位置)
13.若,若的最大值为,则的值是____________
14.如右上图,古希腊数学家把数1,3,6,10,15,21,…叫做
三角数,它们有一定的规律性,第30个三角数与第28个三角数
的差为 。
15.的展开式中各项系数和是128,则展开式中的系数是 。(用数字作答)
16.在△ABC中,A=120°,b=1,面积为,则= 。
三、解答题(本题共6小题,总分70分。解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)已知数列的前项和,
(1)求和;
(2)记,求数列的前项和.
18. (本题满分12分)已知向量.
(1)当时,求的值;
(2)设函数,已知在△ABC中,内角A、B、C的对边分别为,若,求 ()的取值范围.
19.(本题满分12分)第26届世界大学生夏季运动会将于2011年11月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用表示所选志愿者中能担任“礼仪小姐”的人数,试写出的分布列,并求的数学期望。
20.(本题满分12分)
如图,是圆的直径,点在圆上,,交于点,平面,,.
(1)证明:;
(2)求平面与平面所成的锐二面角的余弦值.
21.(本小题满分12分)
已知点是椭圆的右焦点,点、分别是轴、轴上的动点,且满足.若点满足.
(1)求点的轨迹的方程;
(2)设过点任作一直线与点的轨迹交于、两点,直线、与直线 分别交于点、(为坐标原点),试判断是否为定值?若是,求出这个定值;若不是,请说明理由.
22.(本小题满分12分)已知函数 .
(1)讨论函数的单调性;
(2)当时,恒成立,求实数的取值范围;
(3)证明:.
高三数学(理工类)参考答案
一、选择题:
1.D 2.B 3.D 4.B 5.A 6.C 7.B 8.C 9.A 10.C 11.D 12.A
二、填空题:
13.1 14.59 15.—35 16.2
三、解答题:
(Ⅱ) 设数列的前项和为,
时,, -------------------6分
时
故:数列的前项和 ---------------------10分
18.解:(1) …………2分
…………6分
(2)+
由正弦定理得 …………………9分
,,
所以 --------------------12分
(2)依题意,的取值为. ………………………7分
, ,
, . …………………………9分
因此,的分布列如下:
………………10分
. …………………………12分
20.解:(法一)(1)平面平面, .……………1分
又,
平面
而平面
. ………………………………………3分
是圆的直径,.
又,
.
平面,,
平面.
与都是等腰直角三角形.
.
,即(也可由勾股定理证得).………………5分
, 平面.
而平面,
. ………………………………………………………………6分
(法二)(1)同法一,得. ……………………3分
如图,以为坐标原点,垂直于..所在的直线为轴建立空间直角坐标系.
由已知条件得,
. ………4分
由,
得, . ……………6分
(2)由(1)知.
设平面的法向量为,
由 得,
令得,, ………………9分
由已知平面,所以取面的法向量为,
设平面与平面所成的锐二面角为,
则, …………………………11分
平面与平面所成的锐二面角的余弦值为. ……………………12分
(2)(法一)设直线的方程为,.,
则,. ………………………………5分
由,得, 同理得.…………………………7分
,,则. ………8分
由,得,. ……………………9分
则. …………………………11分
因此,的值是定值,且定值为. ………………………12分
(法二)①当时, .,则, .
由 得点的坐标为,则.
由 得点的坐标为,则.
. ………………………………………6分
22解:(1)的定义域为(0,+∞),
当时,>0,故在(0,+∞)单调递增;
当时,<0,故在(0,+∞)单调递减;……………2分
当-1<<0时,令=0,解得.
则当时,>0;时,<0.
故在单调递增,在单调递减. …………4分
(2)因为,所以
当时,恒成立
令,则, ……………6分
因为,由得,
且当时,;当时,.
所以在上递增,在上递减.所以,
故 ……………………8分
输出
是
开始
结束
输入
否
A
B
C
E
F
M
O
x
y
z
A
B
C
E
F
M
O
同课章节目录
