北师大版七年级上册数学 3.1字母表示数 课件(共24张ppt)
文档属性
| 名称 | 北师大版七年级上册数学 3.1字母表示数 课件(共24张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 756.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览



文档简介
3.1 用字母表示数
1只青蛙1张嘴, 2 只眼睛 4 条腿;
2只青蛙2张嘴, 只眼睛 条腿;
3只青蛙3张嘴, 只眼睛 条腿;
4只青蛙4张嘴, 只眼睛 条腿;
……
( )只青蛙( )张嘴,( )只眼睛 ( )条腿。
8
4
6
12
8
16
(四)找一找,猜想归纳:
请观察、比较、猜想下列各算式的规律:
2
2×(2+1)
=
=
3;
1+2
=
=
=
3×(3+1)
2
=
6;
1+2+3
4×(4+1)
2
5×(5+1)
2
=10;
1+2+3+4
1+2+3+4+5
=
15;
1+2+3+…+100
=
=
一般地,有:
=
n×(n+1);
2
1+2+3+…+n
100×(100+1)
2
5050;
做一做
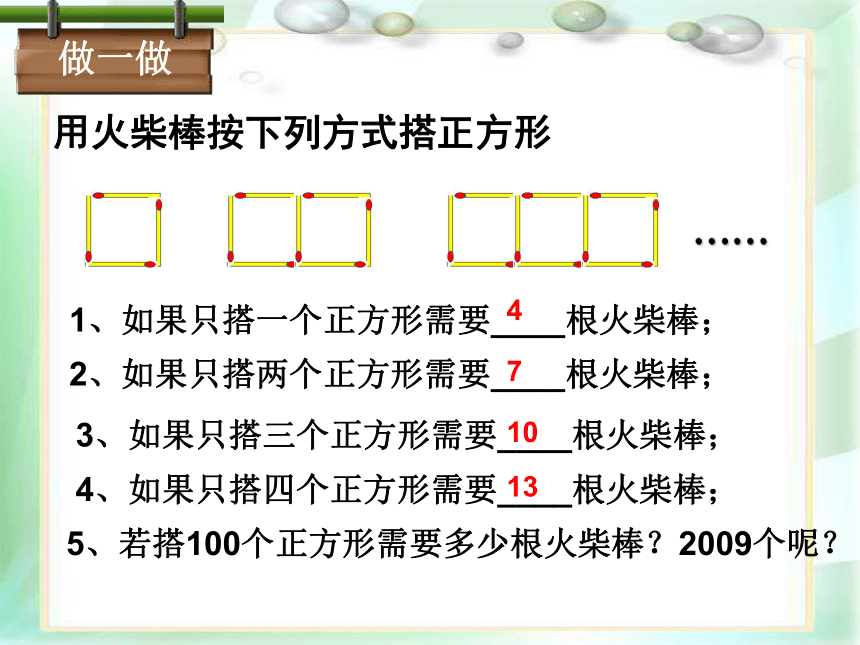
用火柴棒按下列方式搭正方形
1、如果只搭一个正方形需要____根火柴棒;
2、如果只搭两个正方形需要____根火柴棒;
3、如果只搭三个正方形需要____根火柴棒;
4、如果只搭四个正方形需要____根火柴棒;
5、若搭100个正方形需要多少根火柴棒?2009个呢?
……
4
7
10
13
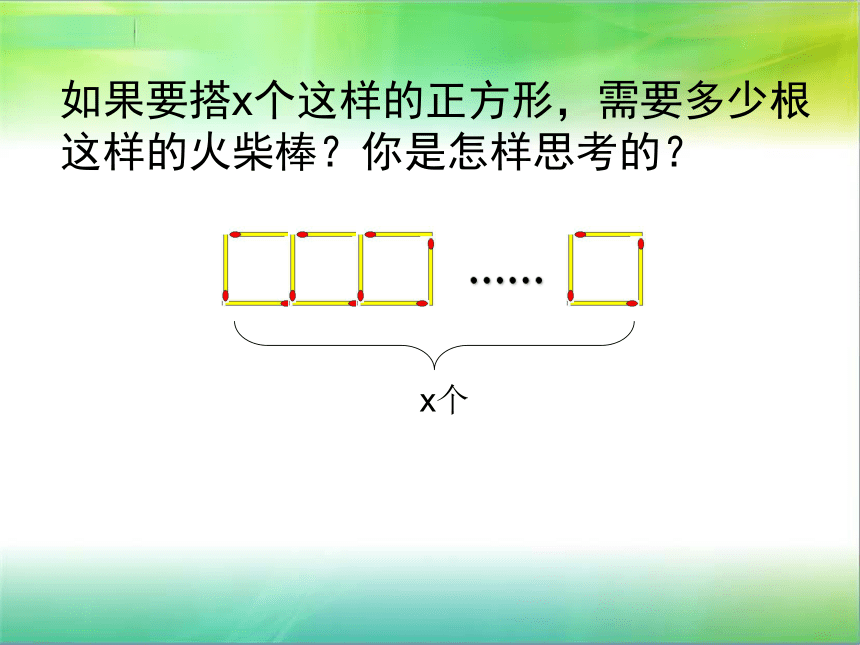
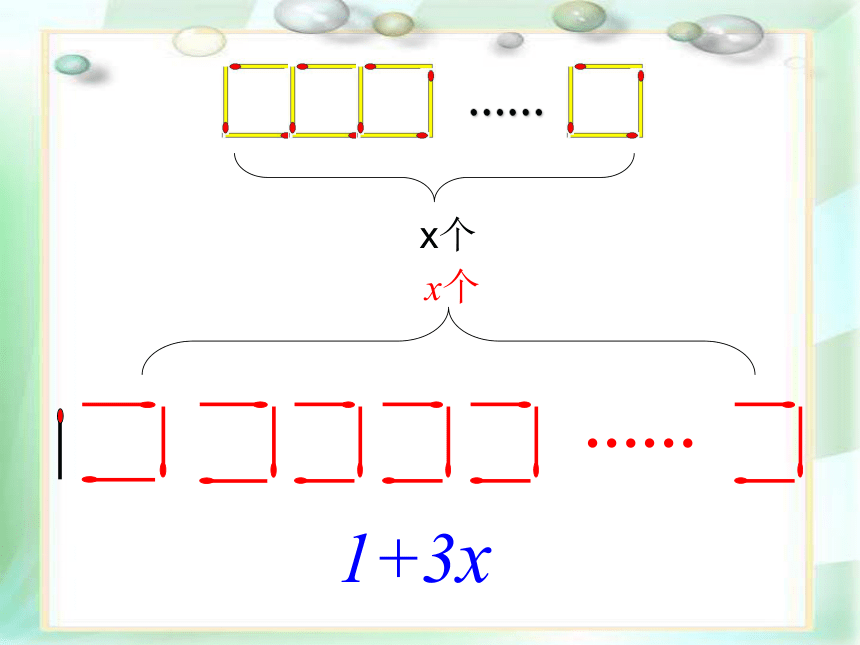
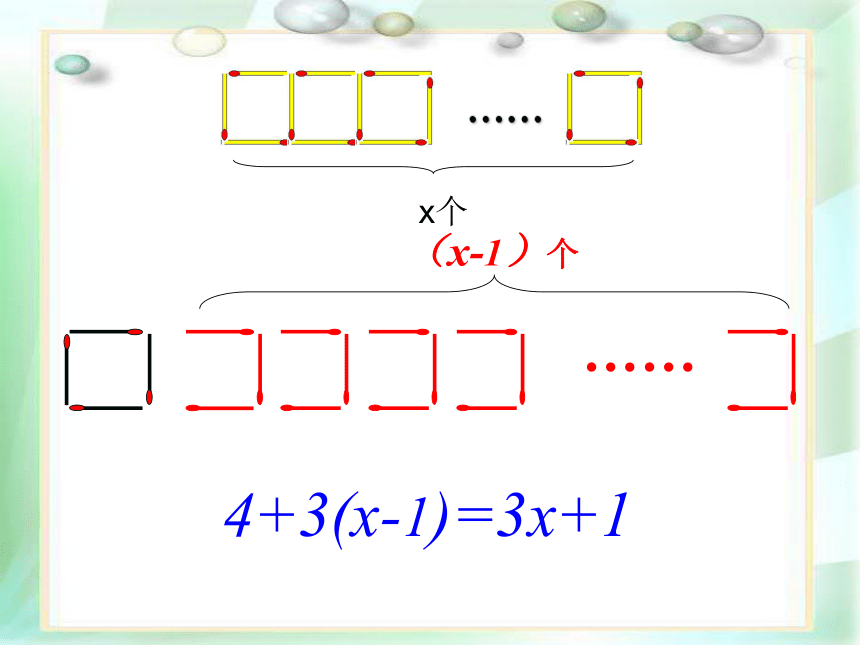
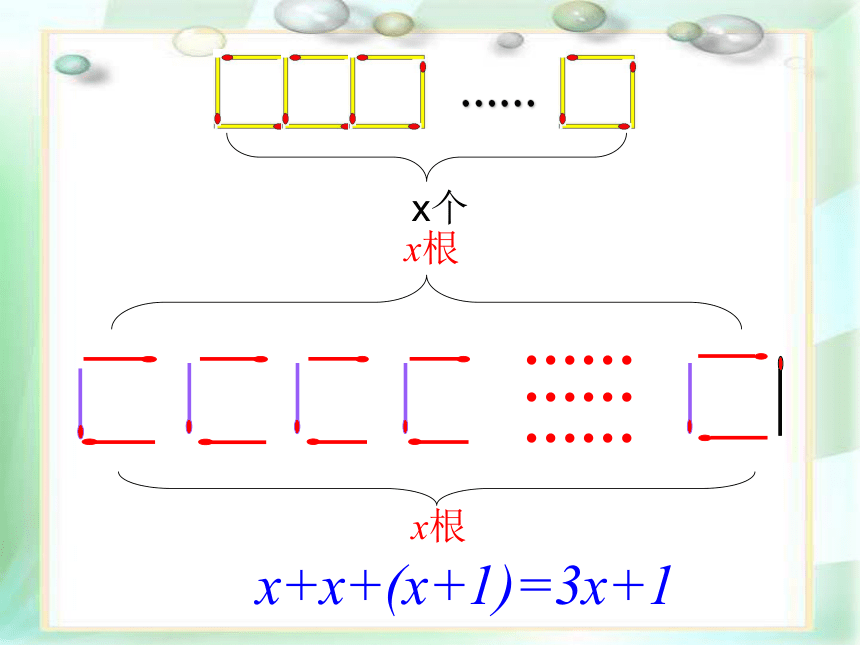
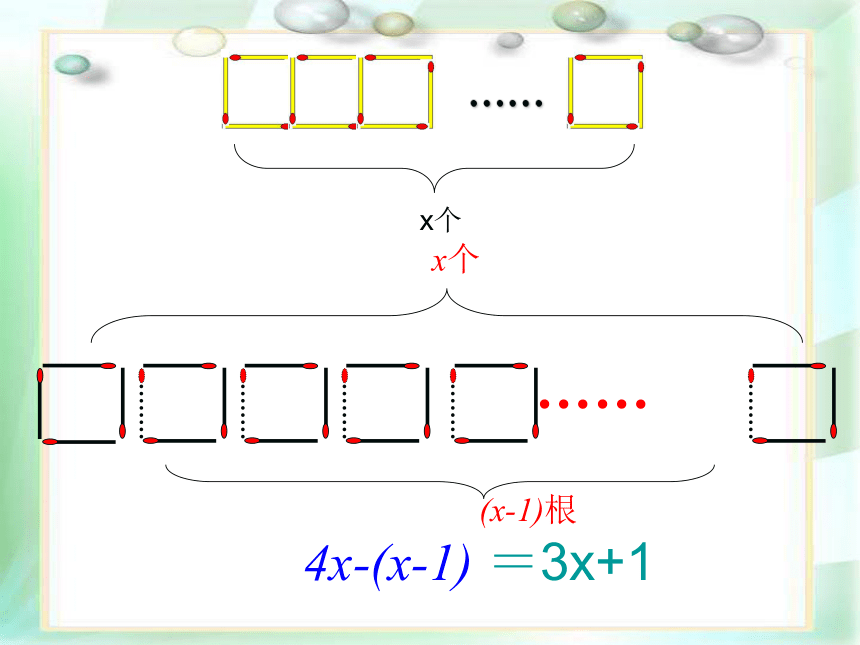
如果要搭x个这样的正方形,需要多少根这样的火柴棒?你是怎样思考的?
……
x个
1+3x
x个
……
……
x个
4+3(x-1)=3x+1
(x-1)个
……
……
x个
x+x+(x+1)=3x+1
x根
x根
……
……
……
……
x个
4x-(x-1) =3x+1
x个
(x-1)根
……
……
x个
6、摆图形
(1)淘气用小正方形摆大门。
摆1个大门需要( )个小正方形,摆2个大门需要( )个小正方形,摆n个大门需要( )个小正方形。
第1个
第2个
……
2×5
1×5
n×5
(2)笑笑用小正方形摆长方形。
长方形编号
第1个
第2个
第3个
……
第n个
…
所需火柴棒个数
……
……
第1个
第2个
第3个
6、摆图形
12
7
17
2+5n
故事
一天的早朝上,国王正在听“小不点”乘号汇报工作:“陛下,因为我和字母x很相近,许多人都把我们混淆。请陛下想出一个对策才行啊!”于是国王传下命令“加号,减号,除号先行退朝,乘号留下议事。”第二天早朝上,零国王宣布了三件事。
(1)x×2 2×x
↘ ↙
2·x
↓
2x
(1)在含有字母的式子里,数字和字母中间的乘号可以记作小圆点,也可省略不写,数字要写在字母前面。
1×b↘
b
b×1↗
(2)1和任何一个字母相乘,1通常省略不写。
a×b b×b
↓ ↓
a·b b
↓
ab
2
(3)字母和字母相乘中间的乘号也可记作小圆点或省略不写。2个相同字母相乘,可以写成平方的形式。
一、在含有字母的式子里,数字和字母中间的乘号可以记作小圆点,也可省略不写,数字要写在字母前面。
二、 1和任何一个字母相乘,1通常省略不写。
三、 2个相同字母相乘,可以写成平方的形式。
小提示:
还知道下列图形面积的计算公式吗?
.
h
a
a
a
b
a
r
a
h
a
b
h
忆一忆
用字母可以表示一些图形的面积公式.
填空:
(1)某地为了治理河山,改造环境,计划在第十个
五年计划期间植树绿化荒山,如果每年植树绿化x公
顷荒山,那么这五年内植树绿化荒山 公顷;
(3)每本练习本m元,每支钢笔n元,甲买了5本练习本,乙买了2支钢笔,两人一共花了 元,甲比乙多花了 元.
(5m+2n)
(5m-2n)
(2) 如果小红用t小时走完的路程为s千米,那么她走这段路程的平均速度为______ 千米/时;
s
t
5x
在填空题中,
如果填入的式子是多项的,
就要把整个式子加上“括号”
字母和字母
相乘时,乘号可以用“.”
表示或省略不
写
数和字母相乘,在省略乘号时,要把数字写在字母的前面
(1)a×2=2×a=2 a =2a
(2)a×b = a b = a b
(3)数与数相乘时要用“×”号。
(4) 出现除式时,用分数表示.
例:a÷2记为 .
(5) 结果含加减运算的,单位前加“( )”.
例:“a+2岁”应为(a+2)岁。
(6) 系数是带分数时,通常带分数要化成假分数.
(7)字母与1相乘,1可以省略不写,如:1×a写做 a .
省略乘号,写出下面各式。
4×b
a×c
1×
χ
χ
χ
×
×5
χ
n×6
=4b
=5
χ
=
χ
χ
=
2
=
ac
=
6n
1、a×4可写成a4。( )
2、b+2可写成2b。 ( )
3、8÷b=8b。( )
4、9×8可改写成98 ( )
5、1×d=d ( )
×
×
×
×
√
6.a ×b ×c写成 abc ( )
7.b ×2 ×c写成 2bc ( )
√
√
将下列算式简写,能省略的则省略。
b×c=
5×c=
b×4=
b×b=
c×1=
c×1×c=
bc
b2
c2
5c
4b
c
1.填空:
(1) 一打铅笔有12枝,n打铅笔有 枝;
(2) 三角形的三边长分别为3a 、4a 、5a,则其周
长为 ;
(3) 如图,某广场四角铺上了四分之一圆形的草地,
平方米.
若圆形的半径为r米,则共有草地
12n
(3a+4a+5a)
r
2
π
练一练
×
10
×
10
2
+
+
c
a
b
2. 我们知道:
23=
×
2
10+3
865=
×
10
2
8
×
10+5
+6
;
;
×
10
2
×
10
5984=
×
10
3
+
+
+
.
类似地,
若某三位数的个位数字为a,十位数字为b,百位数
.
字为c,则此三位数可表示为
5
9
8
4
1只青蛙1张嘴, 2 只眼睛 4 条腿;
2只青蛙2张嘴, 只眼睛 条腿;
3只青蛙3张嘴, 只眼睛 条腿;
4只青蛙4张嘴, 只眼睛 条腿;
……
( )只青蛙( )张嘴,( )只眼睛 ( )条腿。
8
4
6
12
8
16
(四)找一找,猜想归纳:
请观察、比较、猜想下列各算式的规律:
2
2×(2+1)
=
=
3;
1+2
=
=
=
3×(3+1)
2
=
6;
1+2+3
4×(4+1)
2
5×(5+1)
2
=10;
1+2+3+4
1+2+3+4+5
=
15;
1+2+3+…+100
=
=
一般地,有:
=
n×(n+1);
2
1+2+3+…+n
100×(100+1)
2
5050;
做一做
用火柴棒按下列方式搭正方形
1、如果只搭一个正方形需要____根火柴棒;
2、如果只搭两个正方形需要____根火柴棒;
3、如果只搭三个正方形需要____根火柴棒;
4、如果只搭四个正方形需要____根火柴棒;
5、若搭100个正方形需要多少根火柴棒?2009个呢?
……
4
7
10
13
如果要搭x个这样的正方形,需要多少根这样的火柴棒?你是怎样思考的?
……
x个
1+3x
x个
……
……
x个
4+3(x-1)=3x+1
(x-1)个
……
……
x个
x+x+(x+1)=3x+1
x根
x根
……
……
……
……
x个
4x-(x-1) =3x+1
x个
(x-1)根
……
……
x个
6、摆图形
(1)淘气用小正方形摆大门。
摆1个大门需要( )个小正方形,摆2个大门需要( )个小正方形,摆n个大门需要( )个小正方形。
第1个
第2个
……
2×5
1×5
n×5
(2)笑笑用小正方形摆长方形。
长方形编号
第1个
第2个
第3个
……
第n个
…
所需火柴棒个数
……
……
第1个
第2个
第3个
6、摆图形
12
7
17
2+5n
故事
一天的早朝上,国王正在听“小不点”乘号汇报工作:“陛下,因为我和字母x很相近,许多人都把我们混淆。请陛下想出一个对策才行啊!”于是国王传下命令“加号,减号,除号先行退朝,乘号留下议事。”第二天早朝上,零国王宣布了三件事。
(1)x×2 2×x
↘ ↙
2·x
↓
2x
(1)在含有字母的式子里,数字和字母中间的乘号可以记作小圆点,也可省略不写,数字要写在字母前面。
1×b↘
b
b×1↗
(2)1和任何一个字母相乘,1通常省略不写。
a×b b×b
↓ ↓
a·b b
↓
ab
2
(3)字母和字母相乘中间的乘号也可记作小圆点或省略不写。2个相同字母相乘,可以写成平方的形式。
一、在含有字母的式子里,数字和字母中间的乘号可以记作小圆点,也可省略不写,数字要写在字母前面。
二、 1和任何一个字母相乘,1通常省略不写。
三、 2个相同字母相乘,可以写成平方的形式。
小提示:
还知道下列图形面积的计算公式吗?
.
h
a
a
a
b
a
r
a
h
a
b
h
忆一忆
用字母可以表示一些图形的面积公式.
填空:
(1)某地为了治理河山,改造环境,计划在第十个
五年计划期间植树绿化荒山,如果每年植树绿化x公
顷荒山,那么这五年内植树绿化荒山 公顷;
(3)每本练习本m元,每支钢笔n元,甲买了5本练习本,乙买了2支钢笔,两人一共花了 元,甲比乙多花了 元.
(5m+2n)
(5m-2n)
(2) 如果小红用t小时走完的路程为s千米,那么她走这段路程的平均速度为______ 千米/时;
s
t
5x
在填空题中,
如果填入的式子是多项的,
就要把整个式子加上“括号”
字母和字母
相乘时,乘号可以用“.”
表示或省略不
写
数和字母相乘,在省略乘号时,要把数字写在字母的前面
(1)a×2=2×a=2 a =2a
(2)a×b = a b = a b
(3)数与数相乘时要用“×”号。
(4) 出现除式时,用分数表示.
例:a÷2记为 .
(5) 结果含加减运算的,单位前加“( )”.
例:“a+2岁”应为(a+2)岁。
(6) 系数是带分数时,通常带分数要化成假分数.
(7)字母与1相乘,1可以省略不写,如:1×a写做 a .
省略乘号,写出下面各式。
4×b
a×c
1×
χ
χ
χ
×
×5
χ
n×6
=4b
=5
χ
=
χ
χ
=
2
=
ac
=
6n
1、a×4可写成a4。( )
2、b+2可写成2b。 ( )
3、8÷b=8b。( )
4、9×8可改写成98 ( )
5、1×d=d ( )
×
×
×
×
√
6.a ×b ×c写成 abc ( )
7.b ×2 ×c写成 2bc ( )
√
√
将下列算式简写,能省略的则省略。
b×c=
5×c=
b×4=
b×b=
c×1=
c×1×c=
bc
b2
c2
5c
4b
c
1.填空:
(1) 一打铅笔有12枝,n打铅笔有 枝;
(2) 三角形的三边长分别为3a 、4a 、5a,则其周
长为 ;
(3) 如图,某广场四角铺上了四分之一圆形的草地,
平方米.
若圆形的半径为r米,则共有草地
12n
(3a+4a+5a)
r
2
π
练一练
×
10
×
10
2
+
+
c
a
b
2. 我们知道:
23=
×
2
10+3
865=
×
10
2
8
×
10+5
+6
;
;
×
10
2
×
10
5984=
×
10
3
+
+
+
.
类似地,
若某三位数的个位数字为a,十位数字为b,百位数
.
字为c,则此三位数可表示为
5
9
8
4
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
