高中数学:1.3.1空间几何体的表面积和体积
文档属性
| 名称 | 高中数学:1.3.1空间几何体的表面积和体积 |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-05 20:40:50 | ||
图片预览




文档简介
(共48张PPT)
1.3空间几何的表面积与体积
1.3.1 柱体、锥体、台体的表面积和体积
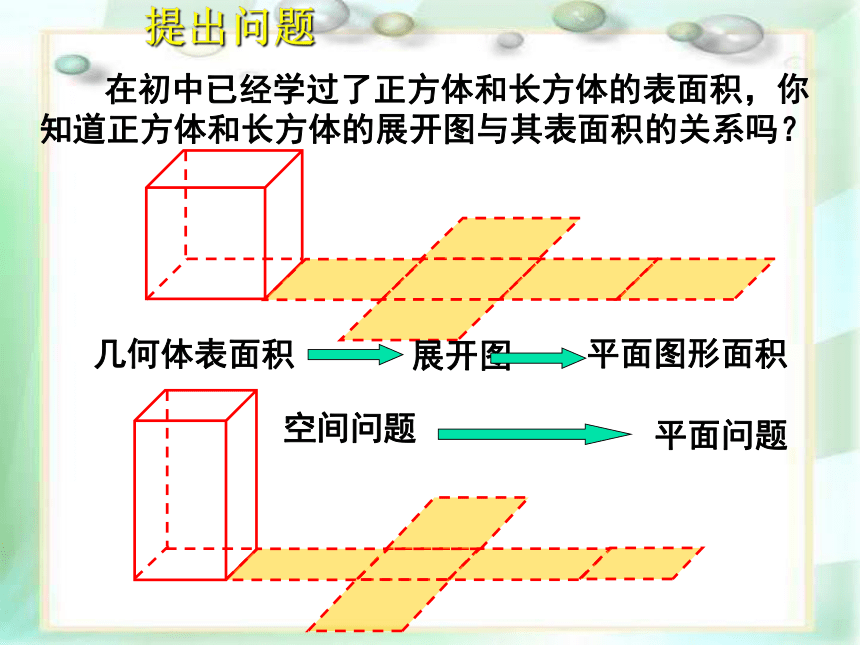
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
提出问题
正方体、长方体是由多个平面围成的几何体,它们的表面积就是各个面的面积的和.
因此,我们可以把它们展成平面图形,利用平面图形求面积的方法,求立体图形的表面积.
引入新课
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
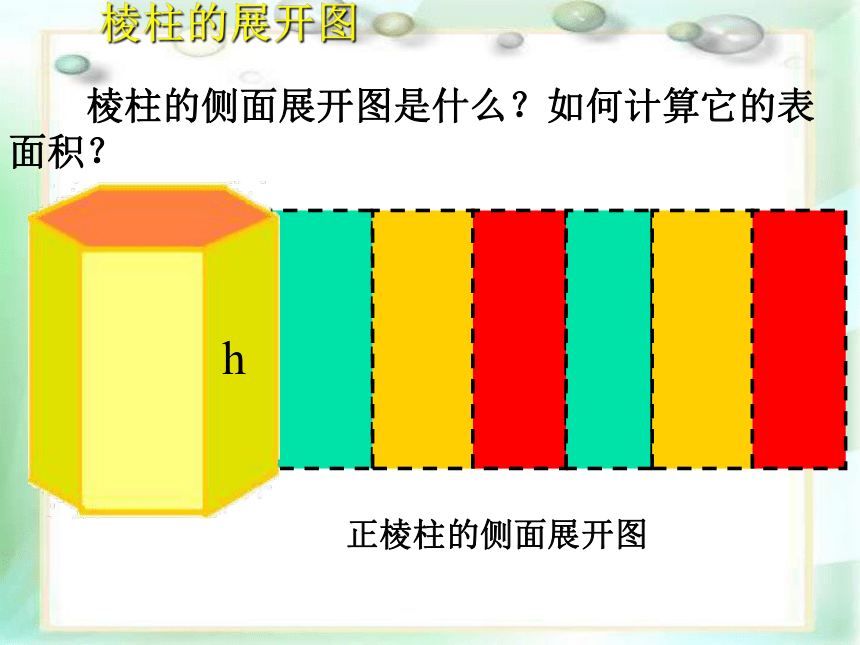
棱柱的侧面展开图是什么?如何计算它的表面积?
h
棱柱的展开图
正棱柱的侧面展开图
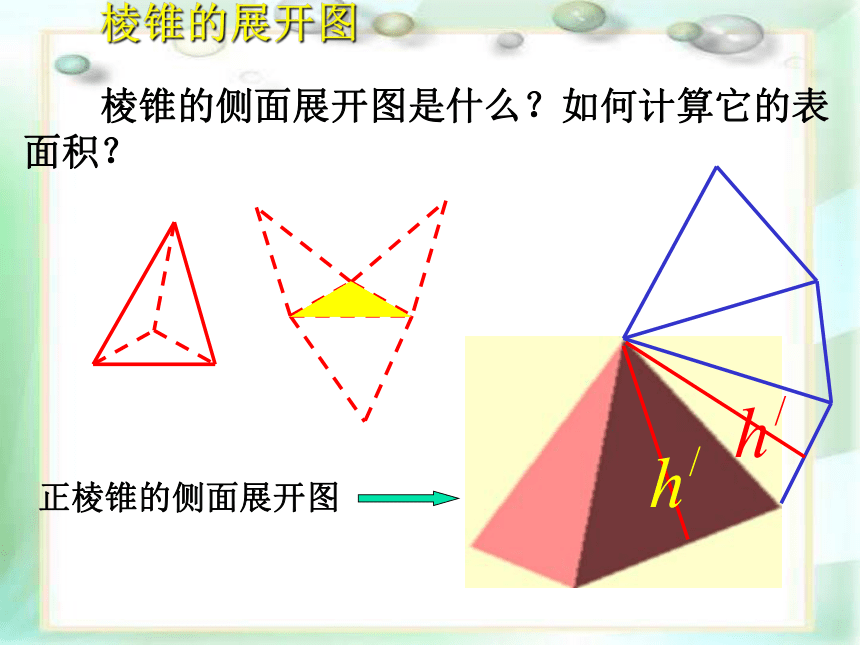
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
正棱锥的侧面展开图
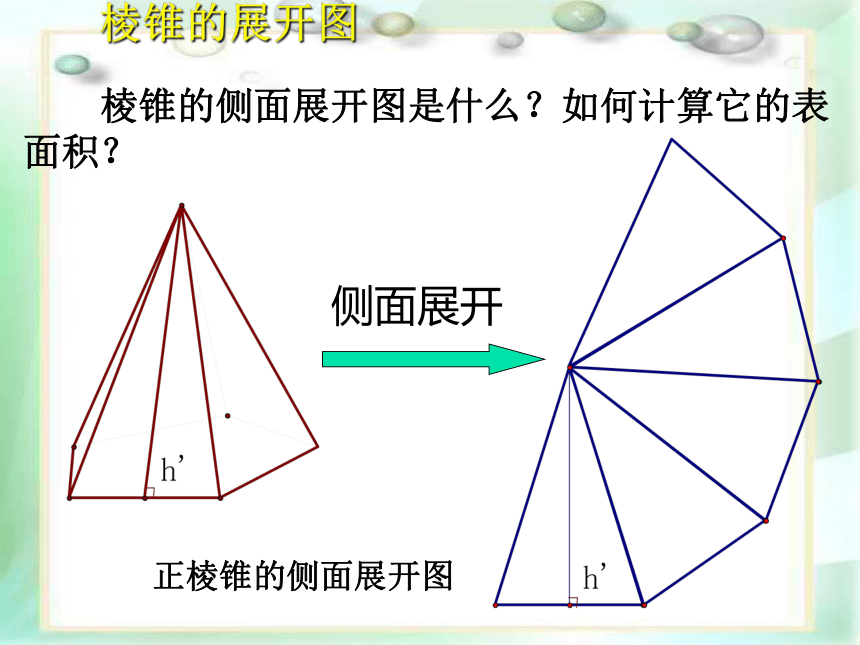
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱锥的侧面展开图
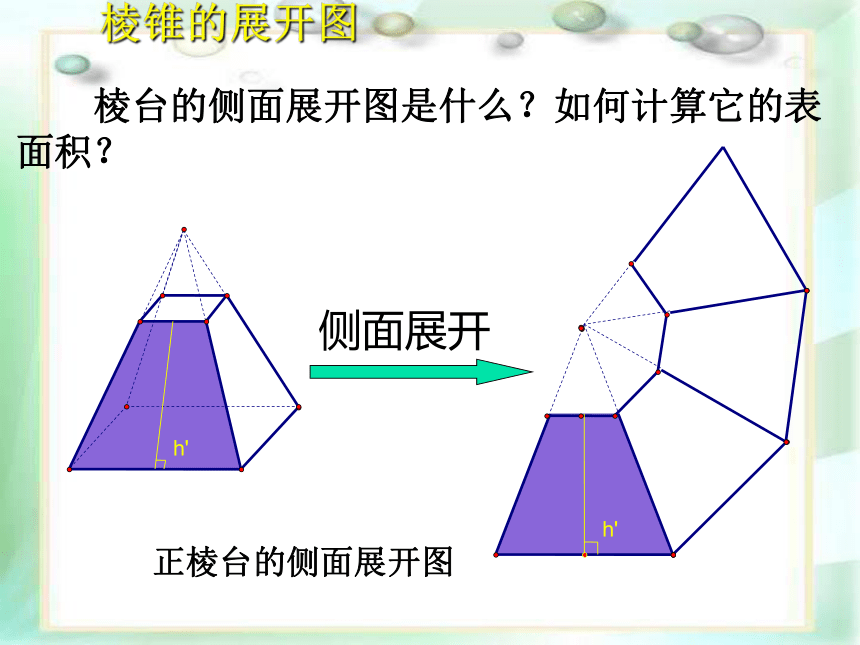
棱台的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
h'
h'
正棱台的侧面展开图
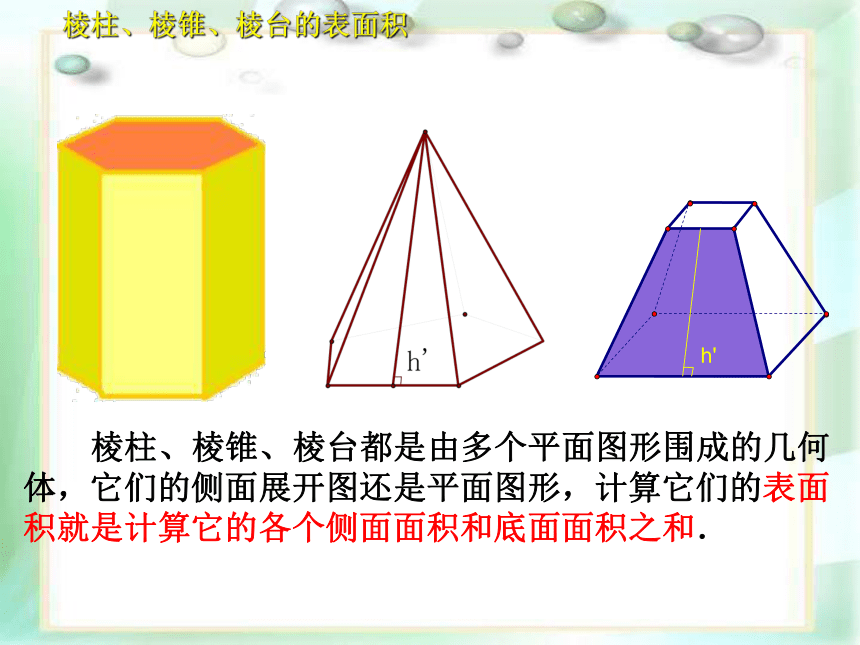
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
例1 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积 .
D
B
C
A
S
分析:四面体的展开图是由四个全等的正三角形组成.
因为BC=a,
所以:
因此,四面体S-ABC 的表面积
交BC于点D.
解:先求 的面积,过点作 ,
典型例题
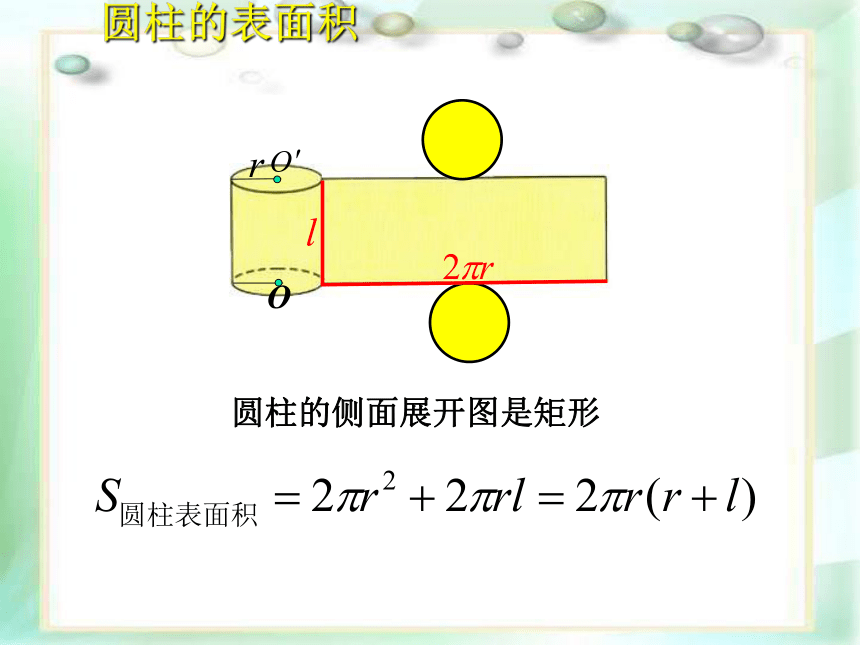
圆柱的表面积
O
圆柱的侧面展开图是矩形
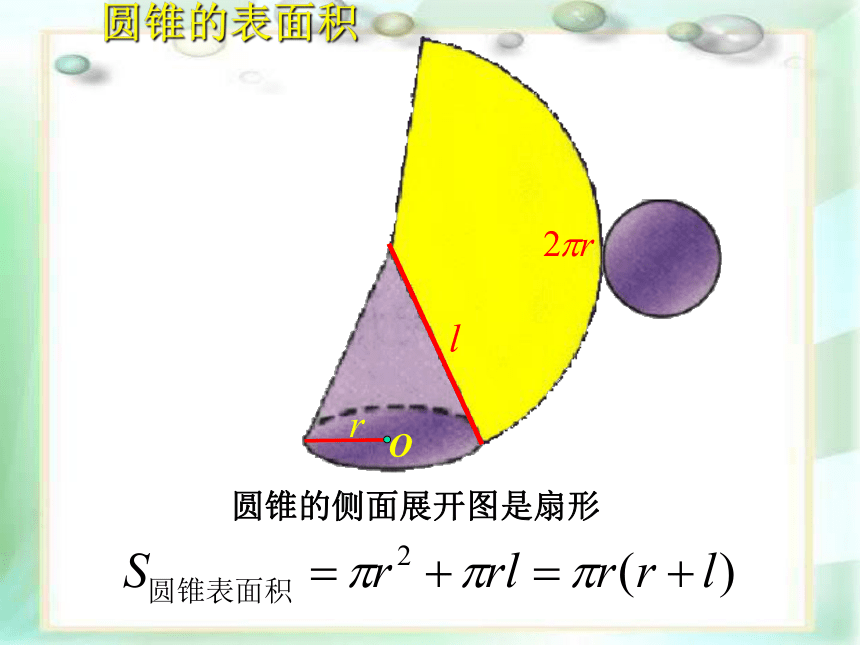
圆锥的表面积
圆锥的侧面展开图是扇形
O
圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 .
O
O’
圆台的侧面展开图是扇环
三者之间关系
O
O’
O
O
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
r’=r
上底扩大
r’=0
上底缩小
例2 如图,一个圆台形花盆盆口直径20 cm,盆底直径为15cm,底部渗水圆孔直径为1.5 cm,盆壁长15cm.那么花盆的表面积约是多少平方厘米( 取3.14,结果精确到1 )?
解:由圆台的表面积公式得 花盆的表面积:
答:花盆的表面积约是999 .
典型例题
以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:
(S为底面面积,h为高).
柱体体积
一般棱柱体积也是:
其中S为底面面积,h为棱柱的高.
圆锥的体积公式:
(其中S为底面面积,h为高)
圆锥体积等于同底等高的圆柱的体积的 .
圆锥体积
探究棱锥与同底等高的棱柱体积之间的关系.
棱锥体积
三棱锥与同底等高的三棱柱的关系
(其中S为底面面积,h为高)
由此可知,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是等于
底面面积乘高的 .
经过探究得知,棱锥也是同底等高的棱柱体积的 .即棱锥的体积:
锥体体积
台体体积
由于圆台(棱台)是由圆锥(棱锥)截成的,因此可以利用两个锥体的体积差.得到圆台(棱台)的体积公式(过程略).
根据台体的特征,如何求台体的体积?
棱台(圆台)的体积公式
其中 , 分别为上、下底面面积,h为圆台(棱台)的高.
台体体积
柱体、锥体、台体的体积公式之间有什么关系?
S为底面面积,h为柱体高
S分别为上、下底面面积,h 为台体高
S为底面面积,h为锥体高
台体体积
上底扩大
上底缩小
例3 有一堆规格相同的铁制(铁的密度是
)六角螺帽共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个( 取3.14)?
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:
所以螺帽的个数为
(个)
答:这堆螺帽大约有252个.
典型例题
柱体、锥体、台体的表面积
各面面积之和
知识小结
展开图
圆台
圆柱
圆锥
柱体、锥体、台体的体积
锥体
台体
柱体
知识小结
生活中常见的球体:
思考:
一 球的概念是什么?
二 球有哪些性质?
三 如何求球的体积
和表面积?
1 球的
概念和
性质
2球的
体积
3 球的
表面积
4 例题
讲解
5 课堂
练习
6 课堂
小结
7 课堂
作业
球
球的概
念和性
质
球的概念
A
B
O
R
C
一
如图所示,半圆以它的直径为旋转轴,旋转所成的曲面叫做球面. 球面所围成的几何体叫做球体,简称球. 半圆的圆心叫球心,图中点O. 连结球心和球面上任意一点的线段叫做球的半径,图中线段R. 连结球面上两点并且经过球心的线段叫做球的直径,图中线段AB.
球的概
念和性
质
球的概念
一
Q
P
O
球面被经过球心的平面截得的圆叫做大圆(如图中红色部分),被不经过球心的截面截得的圆叫做小圆(如图中绿色部分).
球面上两点之间最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,这个弧长叫做两点的球面距离(如图中 的长度就是P、Q两点之间的球面距离 ).
球的概
念和性
质
球的性质
二
d
o1
o2
R
r
用一个平面(如图中平面 )去截一个球,截面是圆面,球的截面有下面的性质:
⑴、球心和截面圆心的连线 垂直于截面(如图直线o1o2垂直于平面 );
⑵、球心到截面的距离d与球的半径R及截面的半径r有下面的关系:
球的体积
我们先来回忆圆面积计算公式的导出方法:
联想
把一个半径为R的圆分成若干等分后重新拼接起来,就可以近似的看成是边长分别为 R和R的矩形,所以圆的面积近似等于 .
A
O
球的体积
类似的,我们也可以用这种方法导出球的体积公式.如图所示,把半球的垂直于底面的半径OA作n等分,过这些等分点用一组平行于底面的平面把半球切割成n层.每一层都近似于圆柱形的“小圆片”,这些“小圆片”的体积之和就是半球的体积.
上面求圆的面积所用的方法为:
分割
近似求和
化成准确值
球的体积
A
O
O1
O2
R
ri
B
“小圆片”的厚度为 ,
第i层“小圆片”的下底面半径
球的体积
球的
表面积
我们再次运用推导球的体积公式时的方法,推导球的表面积公式.
(1)、分割.如下图.把球O的表面分成n个小网格,设它们的表面积分别是△S1,△S2 ,… ,△Sn,显然,球的表面积是S= △S1+ △S2 +…+ △Sn.
把球心O和每个小网格的顶点连接起来,整个球体就被分割成n个“小锥体”.
o
Si
球的
表面积
以第i个网格为底面的“小锥体”,其底面为球面的一部分,
所以是曲的,但如果每个小网格都非常小,就近似于“平”的,每个“小棱体”就近似于棱锥,它们的高近似于球半径R.
o
球的
表面积
(2)、近似求和.
O
由第一步得:
球的
表面积
如果网格分的越细,则: “小锥体”就越接近小棱锥.
R
△Si
△Vi
(3)、化为准确值
例题
讲解
例1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
O
R
x
答:空心钢球的内径约为4.5cm.
由计算器算得:
解:设空心钢球的内径为2xcm,则钢球的质量是
例题
讲解
例2、
如图,圆柱的底面直径与高都等于球的直径.求证:
(1) 球的表面积等于
圆柱的侧面积;
(2) 球的表面积等于
圆柱全面积的2/3.
O
R
证明:(1)设球的半径为
R,则圆柱的底面半径
为R,高为2R,得
O
R
例题
讲解
(2)
课堂
练习
1、已知球O1、球O2、球O3的体积比为
1:8:27,则它们的半径比为———— .
3、火星的半径约是地球半径的一半,
地球表面积约是火星表面积的————倍.
2、赤道上有A、B两点,它们的经度相 差 ,则它们的球面距离为----------(地球半径约6370km,精确到1km).
1:2:3
4
6667km
课堂
小结
了解球的体积、表面积推导的基本思路:分割→求近似和→化为标准和的方法,是一种重要的数学思想方法—极限思想,它是今后要学习的微积分部分“定积分”内容的一个应用;
熟练掌握球的体积、表面积公式:
课堂
作业
作业
习题9.9 P.76 3、4 、5、8
预习小结与复习P.78—P.84
1.3空间几何的表面积与体积
1.3.1 柱体、锥体、台体的表面积和体积
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
提出问题
正方体、长方体是由多个平面围成的几何体,它们的表面积就是各个面的面积的和.
因此,我们可以把它们展成平面图形,利用平面图形求面积的方法,求立体图形的表面积.
引入新课
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
棱柱的侧面展开图是什么?如何计算它的表面积?
h
棱柱的展开图
正棱柱的侧面展开图
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
正棱锥的侧面展开图
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱锥的侧面展开图
棱台的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
h'
h'
正棱台的侧面展开图
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
例1 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积 .
D
B
C
A
S
分析:四面体的展开图是由四个全等的正三角形组成.
因为BC=a,
所以:
因此,四面体S-ABC 的表面积
交BC于点D.
解:先求 的面积,过点作 ,
典型例题
圆柱的表面积
O
圆柱的侧面展开图是矩形
圆锥的表面积
圆锥的侧面展开图是扇形
O
圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 .
O
O’
圆台的侧面展开图是扇环
三者之间关系
O
O’
O
O
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
r’=r
上底扩大
r’=0
上底缩小
例2 如图,一个圆台形花盆盆口直径20 cm,盆底直径为15cm,底部渗水圆孔直径为1.5 cm,盆壁长15cm.那么花盆的表面积约是多少平方厘米( 取3.14,结果精确到1 )?
解:由圆台的表面积公式得 花盆的表面积:
答:花盆的表面积约是999 .
典型例题
以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:
(S为底面面积,h为高).
柱体体积
一般棱柱体积也是:
其中S为底面面积,h为棱柱的高.
圆锥的体积公式:
(其中S为底面面积,h为高)
圆锥体积等于同底等高的圆柱的体积的 .
圆锥体积
探究棱锥与同底等高的棱柱体积之间的关系.
棱锥体积
三棱锥与同底等高的三棱柱的关系
(其中S为底面面积,h为高)
由此可知,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是等于
底面面积乘高的 .
经过探究得知,棱锥也是同底等高的棱柱体积的 .即棱锥的体积:
锥体体积
台体体积
由于圆台(棱台)是由圆锥(棱锥)截成的,因此可以利用两个锥体的体积差.得到圆台(棱台)的体积公式(过程略).
根据台体的特征,如何求台体的体积?
棱台(圆台)的体积公式
其中 , 分别为上、下底面面积,h为圆台(棱台)的高.
台体体积
柱体、锥体、台体的体积公式之间有什么关系?
S为底面面积,h为柱体高
S分别为上、下底面面积,h 为台体高
S为底面面积,h为锥体高
台体体积
上底扩大
上底缩小
例3 有一堆规格相同的铁制(铁的密度是
)六角螺帽共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个( 取3.14)?
解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:
所以螺帽的个数为
(个)
答:这堆螺帽大约有252个.
典型例题
柱体、锥体、台体的表面积
各面面积之和
知识小结
展开图
圆台
圆柱
圆锥
柱体、锥体、台体的体积
锥体
台体
柱体
知识小结
生活中常见的球体:
思考:
一 球的概念是什么?
二 球有哪些性质?
三 如何求球的体积
和表面积?
1 球的
概念和
性质
2球的
体积
3 球的
表面积
4 例题
讲解
5 课堂
练习
6 课堂
小结
7 课堂
作业
球
球的概
念和性
质
球的概念
A
B
O
R
C
一
如图所示,半圆以它的直径为旋转轴,旋转所成的曲面叫做球面. 球面所围成的几何体叫做球体,简称球. 半圆的圆心叫球心,图中点O. 连结球心和球面上任意一点的线段叫做球的半径,图中线段R. 连结球面上两点并且经过球心的线段叫做球的直径,图中线段AB.
球的概
念和性
质
球的概念
一
Q
P
O
球面被经过球心的平面截得的圆叫做大圆(如图中红色部分),被不经过球心的截面截得的圆叫做小圆(如图中绿色部分).
球面上两点之间最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,这个弧长叫做两点的球面距离(如图中 的长度就是P、Q两点之间的球面距离 ).
球的概
念和性
质
球的性质
二
d
o1
o2
R
r
用一个平面(如图中平面 )去截一个球,截面是圆面,球的截面有下面的性质:
⑴、球心和截面圆心的连线 垂直于截面(如图直线o1o2垂直于平面 );
⑵、球心到截面的距离d与球的半径R及截面的半径r有下面的关系:
球的体积
我们先来回忆圆面积计算公式的导出方法:
联想
把一个半径为R的圆分成若干等分后重新拼接起来,就可以近似的看成是边长分别为 R和R的矩形,所以圆的面积近似等于 .
A
O
球的体积
类似的,我们也可以用这种方法导出球的体积公式.如图所示,把半球的垂直于底面的半径OA作n等分,过这些等分点用一组平行于底面的平面把半球切割成n层.每一层都近似于圆柱形的“小圆片”,这些“小圆片”的体积之和就是半球的体积.
上面求圆的面积所用的方法为:
分割
近似求和
化成准确值
球的体积
A
O
O1
O2
R
ri
B
“小圆片”的厚度为 ,
第i层“小圆片”的下底面半径
球的体积
球的
表面积
我们再次运用推导球的体积公式时的方法,推导球的表面积公式.
(1)、分割.如下图.把球O的表面分成n个小网格,设它们的表面积分别是△S1,△S2 ,… ,△Sn,显然,球的表面积是S= △S1+ △S2 +…+ △Sn.
把球心O和每个小网格的顶点连接起来,整个球体就被分割成n个“小锥体”.
o
Si
球的
表面积
以第i个网格为底面的“小锥体”,其底面为球面的一部分,
所以是曲的,但如果每个小网格都非常小,就近似于“平”的,每个“小棱体”就近似于棱锥,它们的高近似于球半径R.
o
球的
表面积
(2)、近似求和.
O
由第一步得:
球的
表面积
如果网格分的越细,则: “小锥体”就越接近小棱锥.
R
△Si
△Vi
(3)、化为准确值
例题
讲解
例1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
O
R
x
答:空心钢球的内径约为4.5cm.
由计算器算得:
解:设空心钢球的内径为2xcm,则钢球的质量是
例题
讲解
例2、
如图,圆柱的底面直径与高都等于球的直径.求证:
(1) 球的表面积等于
圆柱的侧面积;
(2) 球的表面积等于
圆柱全面积的2/3.
O
R
证明:(1)设球的半径为
R,则圆柱的底面半径
为R,高为2R,得
O
R
例题
讲解
(2)
课堂
练习
1、已知球O1、球O2、球O3的体积比为
1:8:27,则它们的半径比为———— .
3、火星的半径约是地球半径的一半,
地球表面积约是火星表面积的————倍.
2、赤道上有A、B两点,它们的经度相 差 ,则它们的球面距离为----------(地球半径约6370km,精确到1km).
1:2:3
4
6667km
课堂
小结
了解球的体积、表面积推导的基本思路:分割→求近似和→化为标准和的方法,是一种重要的数学思想方法—极限思想,它是今后要学习的微积分部分“定积分”内容的一个应用;
熟练掌握球的体积、表面积公式:
课堂
作业
作业
习题9.9 P.76 3、4 、5、8
预习小结与复习P.78—P.84
