2021-2022学年九年级数学北师大版上册《1.1菱形的判定与性质》同步能力达标训练(word版含解析)
文档属性
| 名称 | 2021-2022学年九年级数学北师大版上册《1.1菱形的判定与性质》同步能力达标训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 20:42:58 | ||
图片预览


文档简介
2021年北师大版九年级数学上册《1.1菱形的判定与性质》同步能力达标训练(附答案)
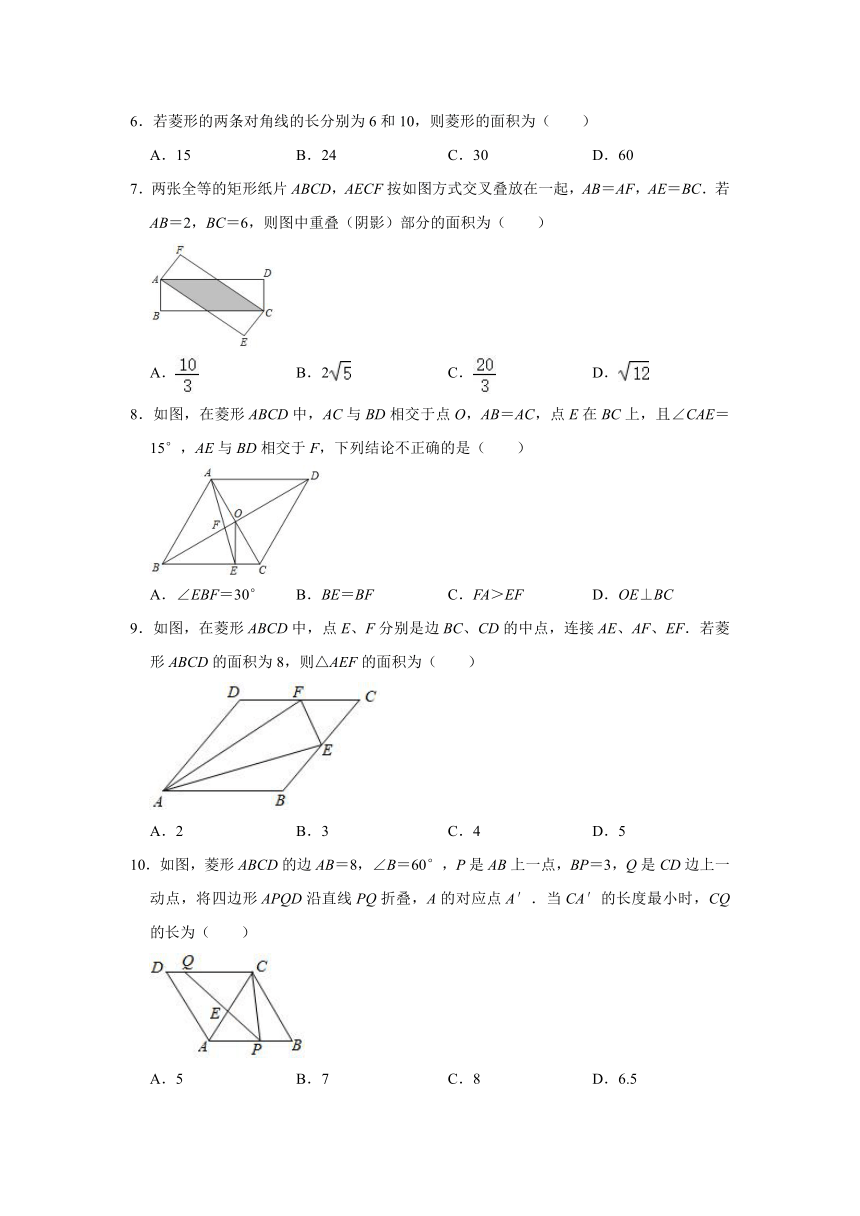
1.关于菱形的性质,以下说法不正确的是( )
A.四条边相等
B.对角线相等
C.对角线互相垂直
D.是轴对称图形
2.如图,在菱形ABCD中,∠A=60°,AD=8.P是AB边上的一点,E,F分别是DP,BP的中点,则线段EF的长为( )
A.8
B.2
C.4
D.2
3.如图,在菱形ABCD中,∠BAD=120°,AC=5,则菱形ABCD的周长是( )
A.25
B.20
C.15
D.10
4.如图,在菱形ABCD中,AC与BD相交于点O,BC的垂直平分线EF分别交BC,AC于点E、F,连接DF,若∠BCD=70°,则∠ADF的度数是( )
A.60°
B.75°
C.80°
D.110°
5.如图,在?ABCD中,AB=BC,下列结论错误的是( )
A.四边形ABCD是菱形
B.AB=AD
C.AO=OC,BO=OD
D.∠BAD=∠ABC
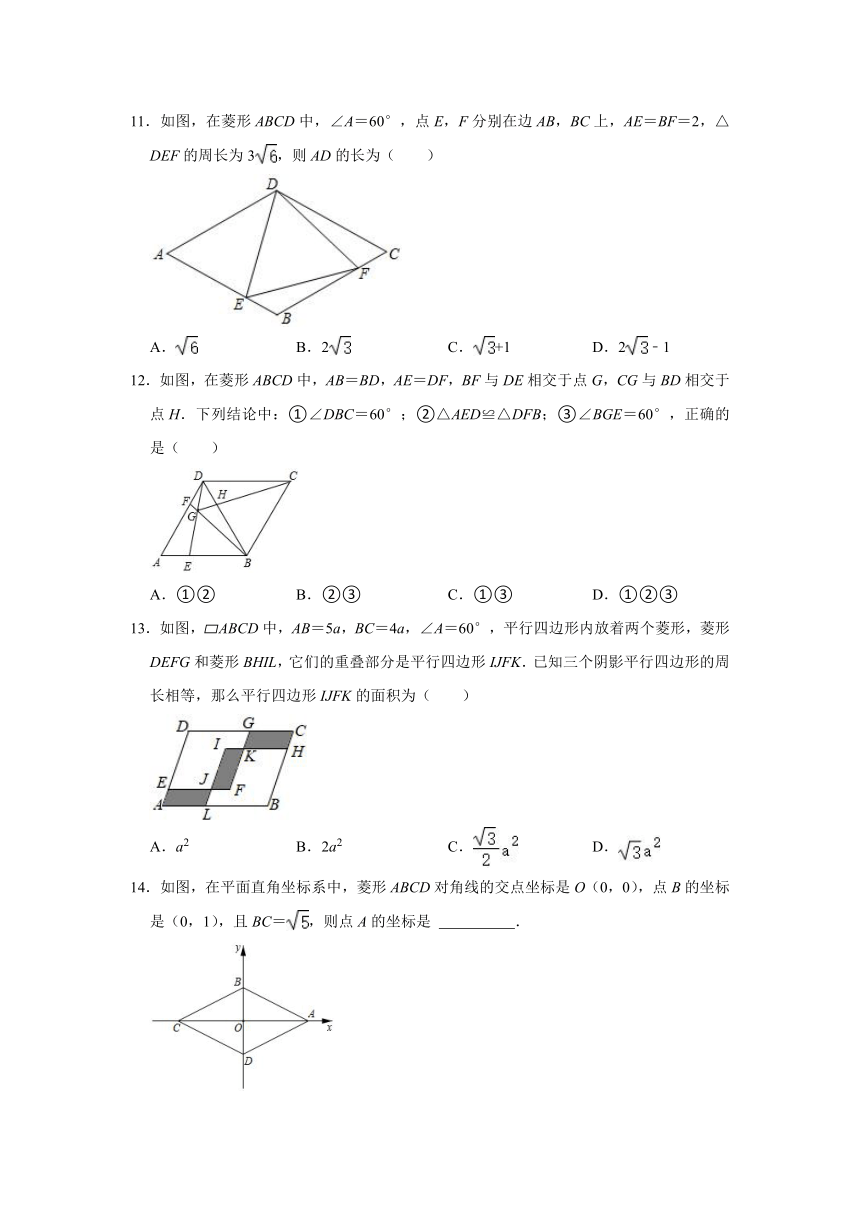
6.若菱形的两条对角线的长分别为6和10,则菱形的面积为( )
A.15
B.24
C.30
D.60
7.两张全等的矩形纸片ABCD,AECF按如图方式交叉叠放在一起,AB=AF,AE=BC.若AB=2,BC=6,则图中重叠(阴影)部分的面积为( )
A.
B.2
C.
D.
8.如图,在菱形ABCD中,AC与BD相交于点O,AB=AC,点E在BC上,且∠CAE=15°,AE与BD相交于F,下列结论不正确的是( )
A.∠EBF=30°
B.BE=BF
C.FA>EF
D.OE⊥BC
9.如图,在菱形ABCD中,点E、F分别是边BC、CD的中点,连接AE、AF、EF.若菱形ABCD的面积为8,则△AEF的面积为( )
A.2
B.3
C.4
D.5
10.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将四边形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )
A.5
B.7
C.8
D.6.5
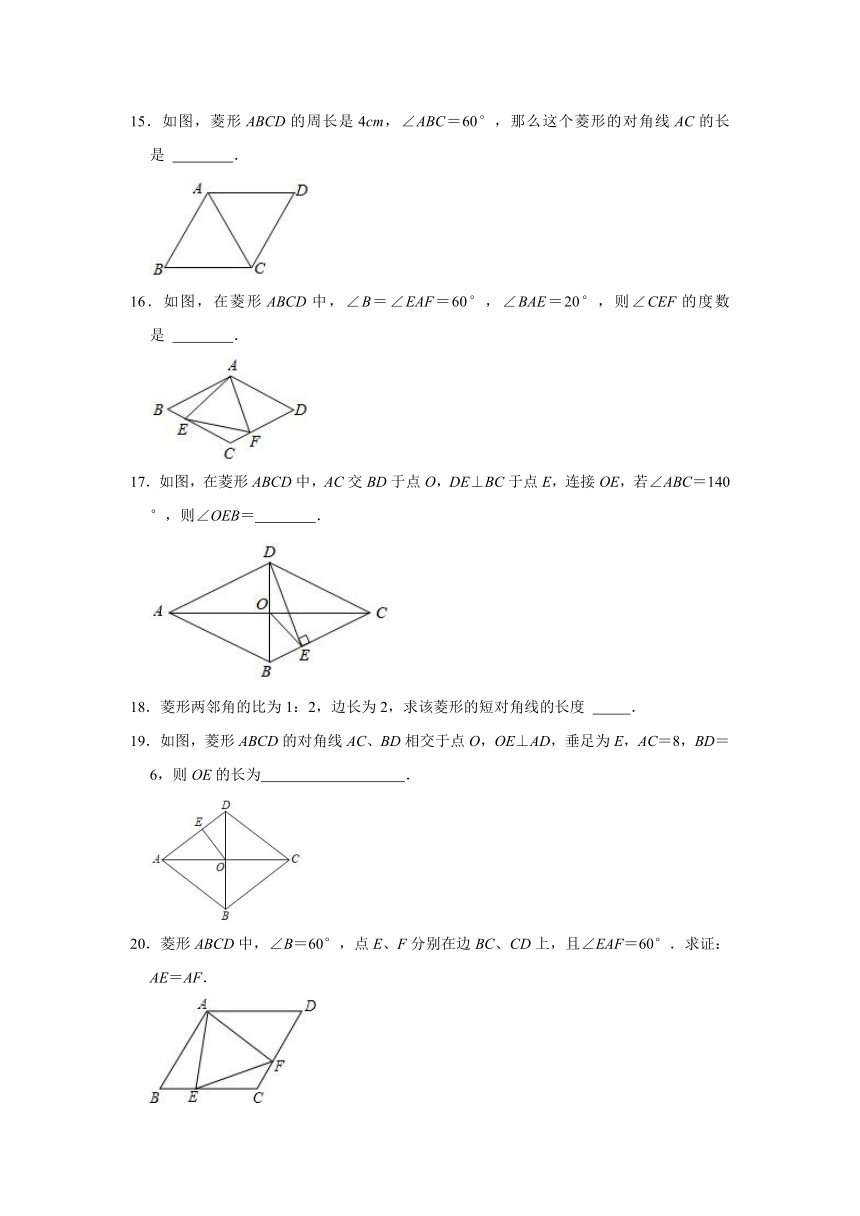
11.如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF=2,△DEF的周长为3,则AD的长为( )
A.
B.2
C.+1
D.2﹣1
12.如图,在菱形ABCD中,AB=BD,AE=DF,BF与DE相交于点G,CG与BD相交于点H.下列结论中:①∠DBC=60°;②△AED≌△DFB;③∠BGE=60°,正确的是( )
A.①②
B.②③
C.①③
D.①②③
13.如图,?ABCD中,AB=5a,BC=4a,∠A=60°,平行四边形内放着两个菱形,菱形DEFG和菱形BHIL,它们的重叠部分是平行四边形IJFK.已知三个阴影平行四边形的周长相等,那么平行四边形IJFK的面积为( )
A.a2
B.2a2
C.
D.
14.如图,在平面直角坐标系中,菱形ABCD对角线的交点坐标是O(0,0),点B的坐标是(0,1),且BC=,则点A的坐标是
.
15.如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是
.
16.如图,在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF的度数是
.
17.如图,在菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠ABC=140°,则∠OEB=
.
18.菱形两邻角的比为1:2,边长为2,求该菱形的短对角线的长度
.
19.如图,菱形ABCD的对角线AC、BD相交于点O,OE⊥AD,垂足为E,AC=8,BD=6,则OE的长为
.
20.菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上,且∠EAF=60°.求证:AE=AF.
21.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)证明四边形BEDF是菱形.
22.如图,已知AD平分∠BAC,AB=AC.
(1)求证:BD=CD;
(2)若点E在AD上,且BE=DC,求证:四边形BECD是菱形.
23.如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE、CF.
(1)求证:四边形AECF是菱形;
(2)若CF=2,∠FAC=30°,∠B=45°,求AB的长.
24.如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=CF,BC=6,求四边形AECF的面积.
25.如图,在Rt△ABC中,∠ACB=90°,D,E分别是边AB,BC的中点,连接DE并延长到点F,使EF=DE,连接CF,BF.
(1)求证:四边形CFBD是菱形;
(2)连接AE,若CF=,DF=2,求AE的长.
26.如图,已知四边形ABCD是菱形,点E,F,G,H分别在线段AB,AD,CD,BC上,BE=DF,EG∥BC,FH∥DC,EG与FH相交于点P.
(1)求证:四边形HCGP是菱形.
(2)若四边形BHPE是菱形,求证:点E是线段AB的中点.
参考答案
1.解:A.菱形的四条边相等,正确,不符合题意,
B.菱形的对角线互相垂直且平分,对角线不一定相等,不正确,符合题意,
C.菱形的对角线互相垂直且平分,正确,不符合题意,
D.菱形是轴对称图形,正确,不符合题意,
故选:B.
2.解:如图连接BD.
∵四边形ABCD是菱形,
∴AD=AB=8,
∵∠A=60°,
∴△ABD是等边三角形,
∴BA=AD=8,
∵PE=ED,PF=FB,
∴EF=BD=4.
故选:C.
3.解:∵四边形ABCD是菱形,
∴AB=BC=AD=CD,∠BAC=∠CAD=∠BAD=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=5=AD=CD,
∴菱形ABCD的周长=4×5=20,
故选:B.
4.解:连接BF,如图所示:
∵四边形ABCD是菱形,
∴∠DCF=∠BCF=∠BCD=35°,AC垂直平分BD,AD∥BC,
∴BF=DF,
∵EF是BC的垂直平分线,
∴BF=CF,
∴DF=CF,
∴∠CDF=∠DCF=35°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADC=180°﹣70°=110°,
∴∠ADF=110°﹣35°=75°,
故选:B.
5.解:∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,
∴∠BAD+∠ABC=180°,
∵AB=BC,
∴平行四边形ABCD是菱形,
∴AB=AD,
故选项A、B、C不符合题意,选项D符合题意,
故选:D.
6.解:菱形的面积=×6×10=30,
故选:C.
7.解:设BC交AE于G,AD交CF于H,如图所示:
∵四边形ABCD、四边形AECF是全等的矩形,
∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,
∴四边形AGCH是平行四边形,
在△ABG和△CEG中,
,
∴△ABG≌△CEG(AAS),
∴AG=CG,
∴四边形AGCH是菱形,
设AG=CG=x,则BG=BC﹣CG=6﹣x,
在Rt△ABG中,由勾股定理得:22+(6﹣x)2=x2,
解得:x=,
∴CG=,
∴菱形AGCH的面积=CG×AB=×2=,
即图中重叠(阴影)部分的面积为,
故选:C.
8.解:如图在菱形ABCD中,AB=CB=AD=CD,
∵AB=AC,
∴AB=CB=AD=CD=AC,
∴△ABC和△ADC都是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵BD=BD(公共边)
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD=∠ABC=30°;
∴∠EBF=30°.
∴A正确;
∵∠ABC=∠BAC=60°,∠CAE=15°,
∴∠BAE=60°﹣15°=45°,
∴∠BEF=180°﹣60°﹣45°=75°,
∴∠BFE=180°﹣30°﹣75°=75°,
∴∠BEF=∠BFE,
∴BE=BF.
∴B正确;
∴FA>EF,
∴C正确;
假设OE⊥BC正确,则∠BEO=90°,
∵∠BEF=75°,
∴∠OEA=90°﹣75°=15°=∠CAE,
∴OE=OA=OC,
∴∠OEC=∠OCE=60°,
∵∠OEC=60°与OE⊥BC相矛盾,
∴假设不成立,
∴OE⊥BC错误,
∴D不正确.故选:D.
9.解:连接AC、BD,交于点O,AC交EF于点G,
∵四边形ABCD是菱形,
∴AO=OC,菱形ABCD的面积为:,
∵点E、F分别是边BC、CD的中点,
∴EF∥BD,EF=BD,
∴AC⊥EF,AG=3CG,
设AC=a,BD=b,
∴=8,即ab=16,
S△AEF===ab=3.
故选:B.
10.解:作CH⊥AB于H,如图,
∵菱形ABCD的边AB=8,∠B=60°,
∴△ABC为等边三角形,
∴CH=AB=4,AH=BH=4,
∵PB=3,
∴HP=1,
在Rt△CHP中,CP===7,
∵梯形APQD沿直线PQ折叠,A的对应点A′,
∴点A′在以P点为圆心,PA为半径的弧上,
∴当点A′在PC上时,CA′的值最小,
∴∠APQ=∠CPQ,而CD∥AB,
∴∠APQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP=7.
故选:B.
11.解:如图,连结BD,作DH⊥AB,垂足为H,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∵∠A=60°,
∴△ABD是等边三角形,∠ABC=180°﹣∠A=120°,
∴AD=BD,∠ABD=∠A=∠ADB=60°,
∴∠DBC=∠ABC﹣∠ABD=120°﹣60°=60°,
∵AE=BF,
∴△ADE≌△BDF(SAS),
∴DE=DF,∠FDB=∠ADE,
∴∠EDF=∠EDB+∠FDB=∠EDB+∠ADE=∠ADB=60°,
∴△DEF是等边三角形,
∵△DEF的周长是3,
∴DE=,
设AH=x,则HE=2﹣x,
∵AD=BD,DH⊥AB,
∴∠ADH=∠ADB=30°,
∴AD=2x,DH=x,
在Rt△DHE中,DH?+HE?=DE?,
∴(x)?+(2﹣x)?=()?,
解得:x=(负值舍去),
∴AD=2x=1+,
故选:C.
12.解:∵ABCD为菱形,
∴AB=AD,
∵AB=BD,
∴△ABD为等边三角形,
∴∠A=∠BDF=60°=∠DBC,
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故①、②正确;
当点E,F分别是AB,AD中点时,
∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,为定值,
故③正确;
综上所述,正确的结论有①②③,
故选:D.
13.解:由题意?ABCD的周长为2(AB+BC)=18a,
又∵三个阴影平行四边形的周长相等,
∴由平移的性质可得:?EALJ的周长=?IJFK的周长=?GKHC的周长=×18a=6a,
∴IJ+JF=EJ+JL=GK+KH=3a,
∴IJ+JL+JF+EJ=6a,IJ+KH+GK+JF=6a,
又∵AB=5a,BC=4a,且四边形DEFG和四边形BHIL是菱形,
∴EF=IL=3a,AE=JF=a,IJ=2a,∠IJF=∠DEF=∠A=60°,
过点I作IP⊥EF,
∴在Rt△IJP中,
JP=IJ=a,IP==a,
∴平行四边形IJFK的面积为JF?IP=a2,
故选:D.
14.解:∵四边形ABCD是菱形,
∴∠BOC=90°,OC=OA,
∵点B的坐标是(0,1),
∴OB=1,
在直角三角形BOC中,BC=,
∴OC==2,
∴点C的坐标(﹣2,0),
∵OA与OC关于原点对称,
∴点A的坐标(2,0).
故答案为:(2,0).
15.解:∵四边形ABCD是菱形,AC是对角线,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,
∵菱形ABCD的周长是4cm,
∴AB=BC=AC=1cm.
故答案为:1cm.
16.解:连接AC,
在菱形ABCD中,AB=CB,
∵∠B=60°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∵∠EAF=60°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即:∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
又∠EAF=∠D=60°,则△AEF是等边三角形,
∴∠AFE=60°,
又∠AEC=∠B+∠BAE=80°,
则∠CEF=80°﹣60°=20°.
故答案为:20°.
17.解:∵四边形ABCD是菱形,
∴O为BD中点,∠DBE=∠ABC=70°.
∵DE⊥BC,
∴OE=OB=OD,
∴∠OEB=∠OBE=70°.
故答案为70°.
18.解:如图,
∵四边形ABCD是菱形,
∴AB∥CD,AB=AD=2,
∴∠A+∠ADC=180°,
∵∠A:∠ADC=1:2,
∴∠A=60°,∠ADC=120°,
∵AD=AB,
∴△ADB为等边三角形,
∴AD=BD=2,
故答案为2.
19.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,DO=BO,
∵AC=8,BD=6,
∴AO=4,DO=3,
∴AD===5,
又∵OE⊥AD,
∴,
∴,
解得OE=,
故答案为:.
20.证明:连接AC,如图,
∵四边形ABCD为菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠2=60°,∠1+∠4=60°,AC=AB,
∴∠ACF=60°,
∵∠EAF=60°,即∠3+∠4=60°,
∴∠1=∠3,
在△AEB和△AFC中,
,
∴△AEB≌△AFC,
∴AE=AF.
21.证明:(1)∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)如图,连接BD,交AC于O,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=CO,BO=DO,
∵AE=CF,
∴EO=FO,
∴四边形BEDF是平行四边形,
又∵BD⊥EF,
∴平行四边形BEDF是菱形.
22.证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD;
(2)∵BD=CD,BE=CD,
∴BD=BE,
∴∠BED=∠BDE,
∵△ABD≌△ACD,
∴∠ADB=∠ADC,
∴∠BED=∠ADC,
∴BE∥DC,
∴四边形BECD为平行四边形,
又∵BD=CD,
∴四边形BECD是菱形.
23.解:(1)证明:如图,
在△ABC中,点D是AC的中点,
∴AD=DC,
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED,
∴△AFD≌△CED(AAS),
∴AF=EC,
∴四边形AECF是平行四边形,
又EF⊥AC,点D是AC的中点,即EF垂直平分AC,
∴AF=FC,
∴平行四边形AECF是菱形.
(2)如图,过点A作AG⊥BC于点G,
由(1)知四边形AECF是菱形,又CF=2,∠FAC=30°,
∴AF∥EC,AE=CF=2,∠FAE=2∠FAC=60°,
∴∠AEB=∠FAE=60°,
∵AG⊥BC,
∴∠AGB=∠AGE=90°,
∴∠GAE=30°,
∴GE=AE=1,AG=GE=,
∵∠B=45°,
∴∠GAB=∠B=45°,
∴BG=AG=,
∴AB=BG=.
24.(1)证明:∵EF垂直平分AC,
∴FA=FC,EA=EC,
∴∠EAC=∠ECA,
∵AF∥BC,
∴∠FAC=∠ECA,
∴∠FAC=∠EAC,
∵EF⊥AC,
∴∠ADF=∠ADE=90°.
∴∠FAC+∠AFE=90°,∠EAC+∠AEF=90°.
∴∠AFE=∠AEF,
∴AF=AE,
∴AF=FC=CE=EA,
∴四边形AECF是菱形;
(2)解:由(1)得:AF=FC=CE=EA,四边形AECF是菱形,
∴∠EAC=∠ECA,
∵∠BAC=90°,
∴∠BAE+∠EAC=∠B+∠ECA=90°,
∴∠BAE=∠B,
∴AE=BE,
∵AB=CF,
∴AB=BE=AE=CE=BC=3,
∴AC===3,△ABE的面积=△ACE的面积,
∴菱形AECF的面积=2△ACE的面积=△ABC的面积=AB×AC=×3×3=.
25.证明:(1)∵点E为BC的中点,
∴CE=BE,
又∵EF=DE,
∴四边形CFBD是平行四边形,
∵D,E分别是边AB,BC的中点,∠ACB=90°,
∴DE∥AC,
∴∠DEB=∠ACB=90°,
即DF⊥CB,
∴四边形CFBD是菱形;
(2)∵D,E分别是边AB,BC的中点,
∴AC=2DE,
∵DF=2DE=2EF,DF=2,
∴AC=2,EF=1,
∵CF=,四边形CFDB是菱形,
∴∠CEF=90°,
∴CE===3,
∵∠ACE=90°,
∴AE===,
即AE的长是.
26.证明:(1)∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∵EG∥BC,FH∥DC,
∴四边形HCGP、四边形BCGE、四边形CDFH都是平行四边形,
∴BE=CG,CH=DF,
∵BE=DF,
∴CG=CH,
∴平行四边形HCGP是菱形;
(2)由(1)可知,BE=CG=CH,
∵四边形BHPE是菱形,
∴BE=BH,
∴BE=BH=CH=BC,
∵四边形ABCD是菱形,
∴AB=BC,
∴BE=AB,
∴点E是线段AB的中点
1.关于菱形的性质,以下说法不正确的是( )
A.四条边相等
B.对角线相等
C.对角线互相垂直
D.是轴对称图形
2.如图,在菱形ABCD中,∠A=60°,AD=8.P是AB边上的一点,E,F分别是DP,BP的中点,则线段EF的长为( )
A.8
B.2
C.4
D.2
3.如图,在菱形ABCD中,∠BAD=120°,AC=5,则菱形ABCD的周长是( )
A.25
B.20
C.15
D.10
4.如图,在菱形ABCD中,AC与BD相交于点O,BC的垂直平分线EF分别交BC,AC于点E、F,连接DF,若∠BCD=70°,则∠ADF的度数是( )
A.60°
B.75°
C.80°
D.110°
5.如图,在?ABCD中,AB=BC,下列结论错误的是( )
A.四边形ABCD是菱形
B.AB=AD
C.AO=OC,BO=OD
D.∠BAD=∠ABC
6.若菱形的两条对角线的长分别为6和10,则菱形的面积为( )
A.15
B.24
C.30
D.60
7.两张全等的矩形纸片ABCD,AECF按如图方式交叉叠放在一起,AB=AF,AE=BC.若AB=2,BC=6,则图中重叠(阴影)部分的面积为( )
A.
B.2
C.
D.
8.如图,在菱形ABCD中,AC与BD相交于点O,AB=AC,点E在BC上,且∠CAE=15°,AE与BD相交于F,下列结论不正确的是( )
A.∠EBF=30°
B.BE=BF
C.FA>EF
D.OE⊥BC
9.如图,在菱形ABCD中,点E、F分别是边BC、CD的中点,连接AE、AF、EF.若菱形ABCD的面积为8,则△AEF的面积为( )
A.2
B.3
C.4
D.5
10.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将四边形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )
A.5
B.7
C.8
D.6.5
11.如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF=2,△DEF的周长为3,则AD的长为( )
A.
B.2
C.+1
D.2﹣1
12.如图,在菱形ABCD中,AB=BD,AE=DF,BF与DE相交于点G,CG与BD相交于点H.下列结论中:①∠DBC=60°;②△AED≌△DFB;③∠BGE=60°,正确的是( )
A.①②
B.②③
C.①③
D.①②③
13.如图,?ABCD中,AB=5a,BC=4a,∠A=60°,平行四边形内放着两个菱形,菱形DEFG和菱形BHIL,它们的重叠部分是平行四边形IJFK.已知三个阴影平行四边形的周长相等,那么平行四边形IJFK的面积为( )
A.a2
B.2a2
C.
D.
14.如图,在平面直角坐标系中,菱形ABCD对角线的交点坐标是O(0,0),点B的坐标是(0,1),且BC=,则点A的坐标是
.
15.如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是
.
16.如图,在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF的度数是
.
17.如图,在菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠ABC=140°,则∠OEB=
.
18.菱形两邻角的比为1:2,边长为2,求该菱形的短对角线的长度
.
19.如图,菱形ABCD的对角线AC、BD相交于点O,OE⊥AD,垂足为E,AC=8,BD=6,则OE的长为
.
20.菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上,且∠EAF=60°.求证:AE=AF.
21.如图,在菱形ABCD中,E,F是对角线AC上的两点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)证明四边形BEDF是菱形.
22.如图,已知AD平分∠BAC,AB=AC.
(1)求证:BD=CD;
(2)若点E在AD上,且BE=DC,求证:四边形BECD是菱形.
23.如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE、CF.
(1)求证:四边形AECF是菱形;
(2)若CF=2,∠FAC=30°,∠B=45°,求AB的长.
24.如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=CF,BC=6,求四边形AECF的面积.
25.如图,在Rt△ABC中,∠ACB=90°,D,E分别是边AB,BC的中点,连接DE并延长到点F,使EF=DE,连接CF,BF.
(1)求证:四边形CFBD是菱形;
(2)连接AE,若CF=,DF=2,求AE的长.
26.如图,已知四边形ABCD是菱形,点E,F,G,H分别在线段AB,AD,CD,BC上,BE=DF,EG∥BC,FH∥DC,EG与FH相交于点P.
(1)求证:四边形HCGP是菱形.
(2)若四边形BHPE是菱形,求证:点E是线段AB的中点.
参考答案
1.解:A.菱形的四条边相等,正确,不符合题意,
B.菱形的对角线互相垂直且平分,对角线不一定相等,不正确,符合题意,
C.菱形的对角线互相垂直且平分,正确,不符合题意,
D.菱形是轴对称图形,正确,不符合题意,
故选:B.
2.解:如图连接BD.
∵四边形ABCD是菱形,
∴AD=AB=8,
∵∠A=60°,
∴△ABD是等边三角形,
∴BA=AD=8,
∵PE=ED,PF=FB,
∴EF=BD=4.
故选:C.
3.解:∵四边形ABCD是菱形,
∴AB=BC=AD=CD,∠BAC=∠CAD=∠BAD=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=5=AD=CD,
∴菱形ABCD的周长=4×5=20,
故选:B.
4.解:连接BF,如图所示:
∵四边形ABCD是菱形,
∴∠DCF=∠BCF=∠BCD=35°,AC垂直平分BD,AD∥BC,
∴BF=DF,
∵EF是BC的垂直平分线,
∴BF=CF,
∴DF=CF,
∴∠CDF=∠DCF=35°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADC=180°﹣70°=110°,
∴∠ADF=110°﹣35°=75°,
故选:B.
5.解:∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,
∴∠BAD+∠ABC=180°,
∵AB=BC,
∴平行四边形ABCD是菱形,
∴AB=AD,
故选项A、B、C不符合题意,选项D符合题意,
故选:D.
6.解:菱形的面积=×6×10=30,
故选:C.
7.解:设BC交AE于G,AD交CF于H,如图所示:
∵四边形ABCD、四边形AECF是全等的矩形,
∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,
∴四边形AGCH是平行四边形,
在△ABG和△CEG中,
,
∴△ABG≌△CEG(AAS),
∴AG=CG,
∴四边形AGCH是菱形,
设AG=CG=x,则BG=BC﹣CG=6﹣x,
在Rt△ABG中,由勾股定理得:22+(6﹣x)2=x2,
解得:x=,
∴CG=,
∴菱形AGCH的面积=CG×AB=×2=,
即图中重叠(阴影)部分的面积为,
故选:C.
8.解:如图在菱形ABCD中,AB=CB=AD=CD,
∵AB=AC,
∴AB=CB=AD=CD=AC,
∴△ABC和△ADC都是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵BD=BD(公共边)
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD=∠ABC=30°;
∴∠EBF=30°.
∴A正确;
∵∠ABC=∠BAC=60°,∠CAE=15°,
∴∠BAE=60°﹣15°=45°,
∴∠BEF=180°﹣60°﹣45°=75°,
∴∠BFE=180°﹣30°﹣75°=75°,
∴∠BEF=∠BFE,
∴BE=BF.
∴B正确;
∴FA>EF,
∴C正确;
假设OE⊥BC正确,则∠BEO=90°,
∵∠BEF=75°,
∴∠OEA=90°﹣75°=15°=∠CAE,
∴OE=OA=OC,
∴∠OEC=∠OCE=60°,
∵∠OEC=60°与OE⊥BC相矛盾,
∴假设不成立,
∴OE⊥BC错误,
∴D不正确.故选:D.
9.解:连接AC、BD,交于点O,AC交EF于点G,
∵四边形ABCD是菱形,
∴AO=OC,菱形ABCD的面积为:,
∵点E、F分别是边BC、CD的中点,
∴EF∥BD,EF=BD,
∴AC⊥EF,AG=3CG,
设AC=a,BD=b,
∴=8,即ab=16,
S△AEF===ab=3.
故选:B.
10.解:作CH⊥AB于H,如图,
∵菱形ABCD的边AB=8,∠B=60°,
∴△ABC为等边三角形,
∴CH=AB=4,AH=BH=4,
∵PB=3,
∴HP=1,
在Rt△CHP中,CP===7,
∵梯形APQD沿直线PQ折叠,A的对应点A′,
∴点A′在以P点为圆心,PA为半径的弧上,
∴当点A′在PC上时,CA′的值最小,
∴∠APQ=∠CPQ,而CD∥AB,
∴∠APQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP=7.
故选:B.
11.解:如图,连结BD,作DH⊥AB,垂足为H,
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∵∠A=60°,
∴△ABD是等边三角形,∠ABC=180°﹣∠A=120°,
∴AD=BD,∠ABD=∠A=∠ADB=60°,
∴∠DBC=∠ABC﹣∠ABD=120°﹣60°=60°,
∵AE=BF,
∴△ADE≌△BDF(SAS),
∴DE=DF,∠FDB=∠ADE,
∴∠EDF=∠EDB+∠FDB=∠EDB+∠ADE=∠ADB=60°,
∴△DEF是等边三角形,
∵△DEF的周长是3,
∴DE=,
设AH=x,则HE=2﹣x,
∵AD=BD,DH⊥AB,
∴∠ADH=∠ADB=30°,
∴AD=2x,DH=x,
在Rt△DHE中,DH?+HE?=DE?,
∴(x)?+(2﹣x)?=()?,
解得:x=(负值舍去),
∴AD=2x=1+,
故选:C.
12.解:∵ABCD为菱形,
∴AB=AD,
∵AB=BD,
∴△ABD为等边三角形,
∴∠A=∠BDF=60°=∠DBC,
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故①、②正确;
当点E,F分别是AB,AD中点时,
∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,为定值,
故③正确;
综上所述,正确的结论有①②③,
故选:D.
13.解:由题意?ABCD的周长为2(AB+BC)=18a,
又∵三个阴影平行四边形的周长相等,
∴由平移的性质可得:?EALJ的周长=?IJFK的周长=?GKHC的周长=×18a=6a,
∴IJ+JF=EJ+JL=GK+KH=3a,
∴IJ+JL+JF+EJ=6a,IJ+KH+GK+JF=6a,
又∵AB=5a,BC=4a,且四边形DEFG和四边形BHIL是菱形,
∴EF=IL=3a,AE=JF=a,IJ=2a,∠IJF=∠DEF=∠A=60°,
过点I作IP⊥EF,
∴在Rt△IJP中,
JP=IJ=a,IP==a,
∴平行四边形IJFK的面积为JF?IP=a2,
故选:D.
14.解:∵四边形ABCD是菱形,
∴∠BOC=90°,OC=OA,
∵点B的坐标是(0,1),
∴OB=1,
在直角三角形BOC中,BC=,
∴OC==2,
∴点C的坐标(﹣2,0),
∵OA与OC关于原点对称,
∴点A的坐标(2,0).
故答案为:(2,0).
15.解:∵四边形ABCD是菱形,AC是对角线,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,
∵菱形ABCD的周长是4cm,
∴AB=BC=AC=1cm.
故答案为:1cm.
16.解:连接AC,
在菱形ABCD中,AB=CB,
∵∠B=60°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∵∠EAF=60°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即:∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
又∠EAF=∠D=60°,则△AEF是等边三角形,
∴∠AFE=60°,
又∠AEC=∠B+∠BAE=80°,
则∠CEF=80°﹣60°=20°.
故答案为:20°.
17.解:∵四边形ABCD是菱形,
∴O为BD中点,∠DBE=∠ABC=70°.
∵DE⊥BC,
∴OE=OB=OD,
∴∠OEB=∠OBE=70°.
故答案为70°.
18.解:如图,
∵四边形ABCD是菱形,
∴AB∥CD,AB=AD=2,
∴∠A+∠ADC=180°,
∵∠A:∠ADC=1:2,
∴∠A=60°,∠ADC=120°,
∵AD=AB,
∴△ADB为等边三角形,
∴AD=BD=2,
故答案为2.
19.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,DO=BO,
∵AC=8,BD=6,
∴AO=4,DO=3,
∴AD===5,
又∵OE⊥AD,
∴,
∴,
解得OE=,
故答案为:.
20.证明:连接AC,如图,
∵四边形ABCD为菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠2=60°,∠1+∠4=60°,AC=AB,
∴∠ACF=60°,
∵∠EAF=60°,即∠3+∠4=60°,
∴∠1=∠3,
在△AEB和△AFC中,
,
∴△AEB≌△AFC,
∴AE=AF.
21.证明:(1)∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)如图,连接BD,交AC于O,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=CO,BO=DO,
∵AE=CF,
∴EO=FO,
∴四边形BEDF是平行四边形,
又∵BD⊥EF,
∴平行四边形BEDF是菱形.
22.证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD;
(2)∵BD=CD,BE=CD,
∴BD=BE,
∴∠BED=∠BDE,
∵△ABD≌△ACD,
∴∠ADB=∠ADC,
∴∠BED=∠ADC,
∴BE∥DC,
∴四边形BECD为平行四边形,
又∵BD=CD,
∴四边形BECD是菱形.
23.解:(1)证明:如图,
在△ABC中,点D是AC的中点,
∴AD=DC,
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED,
∴△AFD≌△CED(AAS),
∴AF=EC,
∴四边形AECF是平行四边形,
又EF⊥AC,点D是AC的中点,即EF垂直平分AC,
∴AF=FC,
∴平行四边形AECF是菱形.
(2)如图,过点A作AG⊥BC于点G,
由(1)知四边形AECF是菱形,又CF=2,∠FAC=30°,
∴AF∥EC,AE=CF=2,∠FAE=2∠FAC=60°,
∴∠AEB=∠FAE=60°,
∵AG⊥BC,
∴∠AGB=∠AGE=90°,
∴∠GAE=30°,
∴GE=AE=1,AG=GE=,
∵∠B=45°,
∴∠GAB=∠B=45°,
∴BG=AG=,
∴AB=BG=.
24.(1)证明:∵EF垂直平分AC,
∴FA=FC,EA=EC,
∴∠EAC=∠ECA,
∵AF∥BC,
∴∠FAC=∠ECA,
∴∠FAC=∠EAC,
∵EF⊥AC,
∴∠ADF=∠ADE=90°.
∴∠FAC+∠AFE=90°,∠EAC+∠AEF=90°.
∴∠AFE=∠AEF,
∴AF=AE,
∴AF=FC=CE=EA,
∴四边形AECF是菱形;
(2)解:由(1)得:AF=FC=CE=EA,四边形AECF是菱形,
∴∠EAC=∠ECA,
∵∠BAC=90°,
∴∠BAE+∠EAC=∠B+∠ECA=90°,
∴∠BAE=∠B,
∴AE=BE,
∵AB=CF,
∴AB=BE=AE=CE=BC=3,
∴AC===3,△ABE的面积=△ACE的面积,
∴菱形AECF的面积=2△ACE的面积=△ABC的面积=AB×AC=×3×3=.
25.证明:(1)∵点E为BC的中点,
∴CE=BE,
又∵EF=DE,
∴四边形CFBD是平行四边形,
∵D,E分别是边AB,BC的中点,∠ACB=90°,
∴DE∥AC,
∴∠DEB=∠ACB=90°,
即DF⊥CB,
∴四边形CFBD是菱形;
(2)∵D,E分别是边AB,BC的中点,
∴AC=2DE,
∵DF=2DE=2EF,DF=2,
∴AC=2,EF=1,
∵CF=,四边形CFDB是菱形,
∴∠CEF=90°,
∴CE===3,
∵∠ACE=90°,
∴AE===,
即AE的长是.
26.证明:(1)∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∵EG∥BC,FH∥DC,
∴四边形HCGP、四边形BCGE、四边形CDFH都是平行四边形,
∴BE=CG,CH=DF,
∵BE=DF,
∴CG=CH,
∴平行四边形HCGP是菱形;
(2)由(1)可知,BE=CG=CH,
∵四边形BHPE是菱形,
∴BE=BH,
∴BE=BH=CH=BC,
∵四边形ABCD是菱形,
∴AB=BC,
∴BE=AB,
∴点E是线段AB的中点
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
