2021-2022学年九年级数学北师大版上册《1.2矩形的判定与性质》同步能力达标训练(word版含解析)
文档属性
| 名称 | 2021-2022学年九年级数学北师大版上册《1.2矩形的判定与性质》同步能力达标训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 863.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 20:40:00 | ||
图片预览


文档简介
2021年北师大版九年级数学上册《1.2矩形的判定与性质》同步能力达标训练(附答案)
1.如图,在矩形ABCD中,∠AOB=120°,AD=3,则AC=( )
A.6
B.
C.5
D.
2.矩形的三个顶点坐标分别是(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),那么第四个顶点坐标是( )
A.(1,﹣4)
B.(﹣8,﹣4)
C.(1,﹣3)
D.(3,﹣4)
3.下列性质中菱形有矩形不一定具有的性质是( )
A.对角线互相垂直
B.对角线互相平分
C.对角线相等
D.既是轴对称图形又是中心对称图形
4.如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( )
A.5
B.2.5
C.2.4
D.3
5.在四边形ABCD中,AC,BD交于点O.在下列各组条件中,不能判定四边形ABCD为矩形的是( )
A.∠A=∠C,∠B+∠C=180°,AC⊥BD
B.AO=CO,BO=DO,∠A=90°
C.∠A=∠B=90°,AC=BD
D.AB=CD,AD=BC,AC=BD
6.如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )
A.10
B.11
C.12
D.13
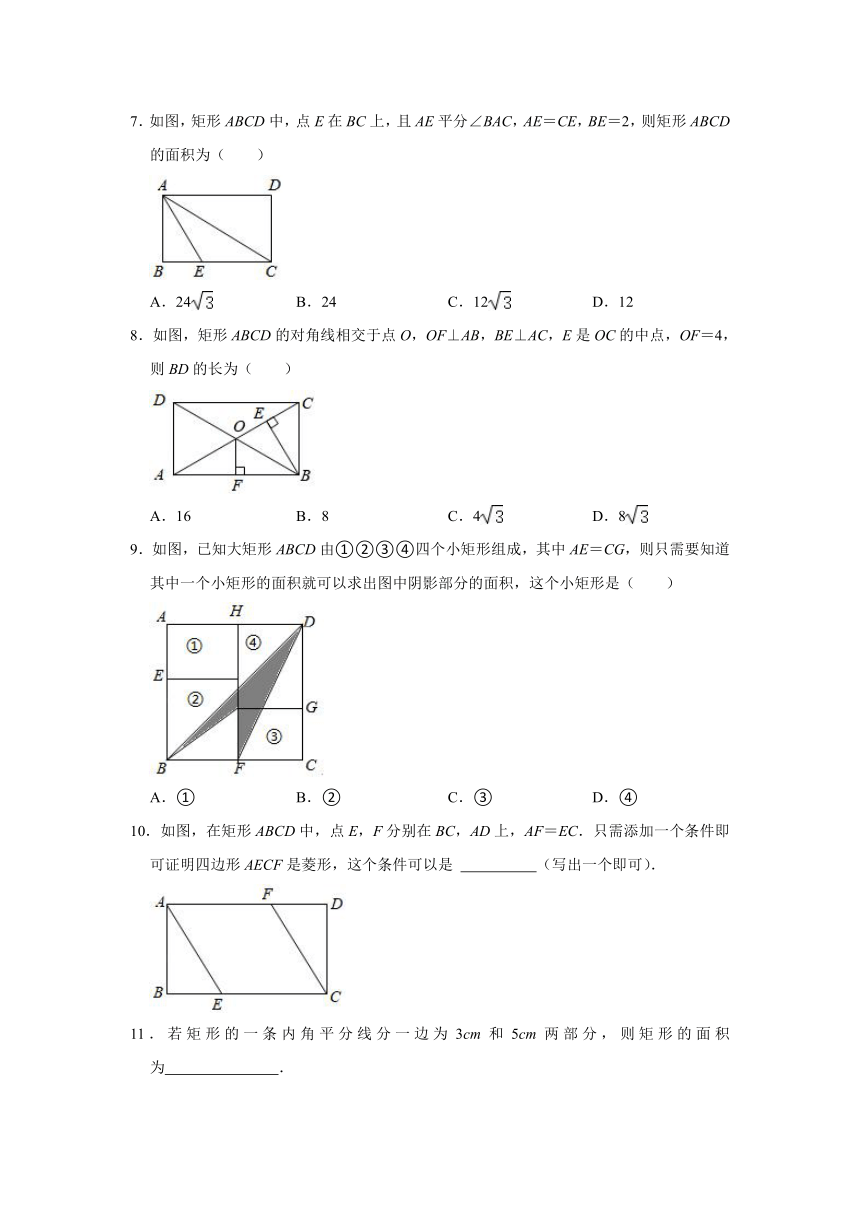
7.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24
B.24
C.12
D.12
8.如图,矩形ABCD的对角线相交于点O,OF⊥AB,BE⊥AC,E是OC的中点,OF=4,则BD的长为( )
A.16
B.8
C.4
D.8
9.如图,已知大矩形ABCD由①②③④四个小矩形组成,其中AE=CG,则只需要知道其中一个小矩形的面积就可以求出图中阴影部分的面积,这个小矩形是( )
A.①
B.②
C.③
D.④
10.如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC.只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是
(写出一个即可).
11.若矩形的一条内角平分线分一边为3cm和5cm两部分,则矩形的面积为
.
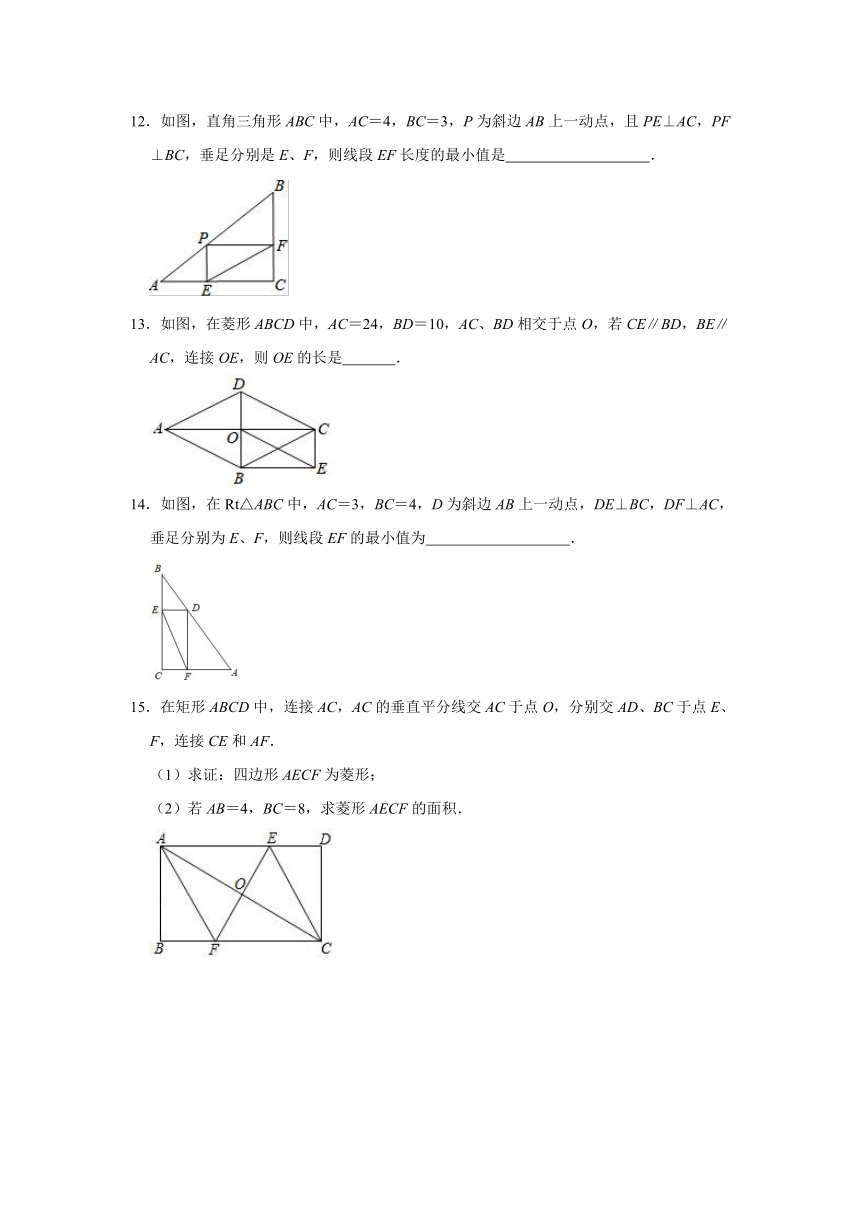
12.如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是
.
13.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE∥BD,BE∥AC,连接OE,则OE的长是
.
14.如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F,则线段EF的最小值为
.
15.在矩形ABCD中,连接AC,AC的垂直平分线交AC于点O,分别交AD、BC于点E、F,连接CE和AF.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形AECF的面积.
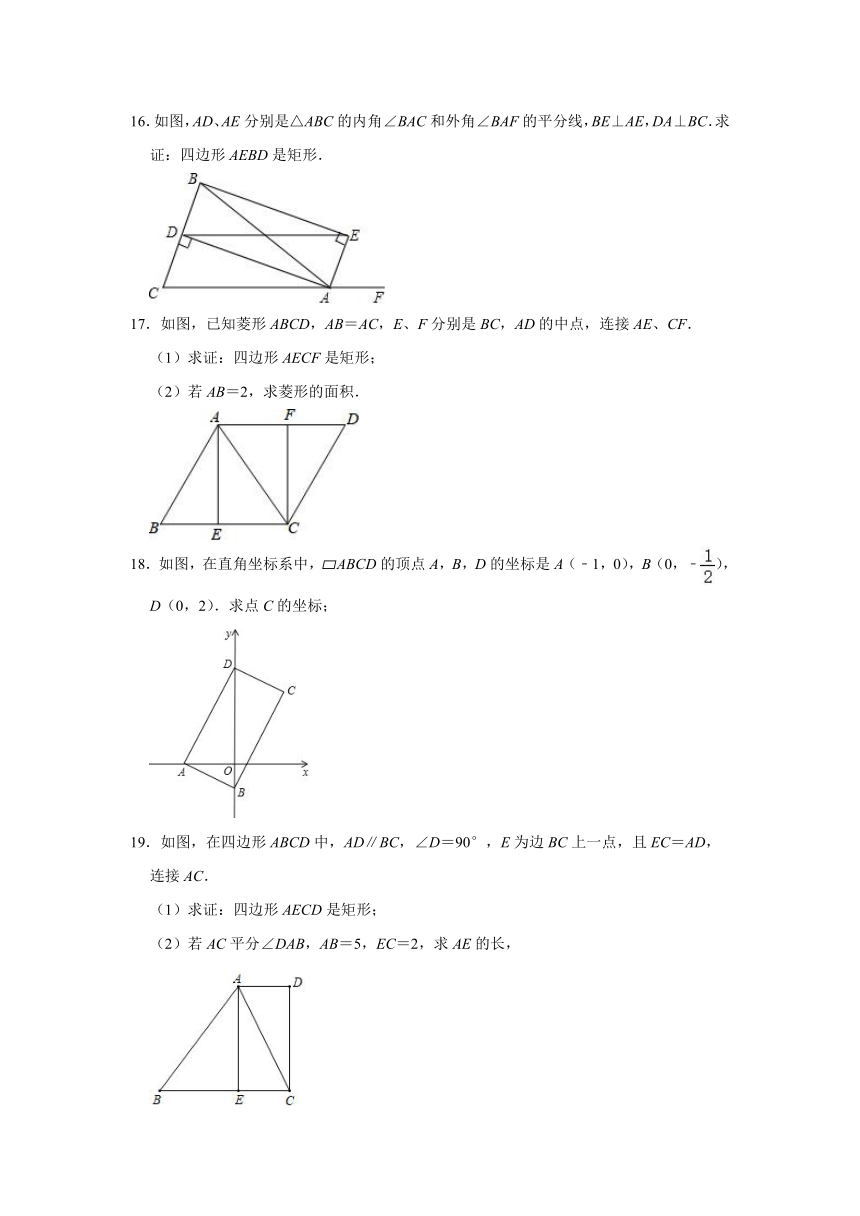
16.如图,AD、AE分别是△ABC的内角∠BAC和外角∠BAF的平分线,BE⊥AE,DA⊥BC.求证:四边形AEBD是矩形.
17.如图,已知菱形ABCD,AB=AC,E、F分别是BC,AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=2,求菱形的面积.
18.如图,在直角坐标系中,?ABCD的顶点A,B,D的坐标是A(﹣1,0),B(0,﹣),D(0,2).求点C的坐标;
19.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连接AC.
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
20.如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度(AE=CF)向C、A运动,其速度为0.5cm/s.
(1)当E与F不重合时,求证:四边形DEBF是平行四边形;
(2)点E,F在AC上运动过程中,求当运动时间t为何值时,以D、E、B、F为顶点的四边形是矩形.
参考答案
1.解:∵∠AOB=120°,
∴∠AOD=60°,
∵矩形对角线相等且互相平分,
∴AO=DO,
∴△ADO为等边三角形,
∴AO=AD,AC=2AO=2AD=6.
故选:A.
2.解:如图所示:
∵矩形ABCD中,A、B、D三点的坐标分别(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),
∴点C的横坐标与B的横坐标相等,纵坐标与D的纵坐标相等,
即C的坐标是(1,﹣4).
故选:A.
3.解:菱形的对角线互相平分、垂直、对角线平分一组对角,
矩形的对角线互相平分、相等,
故菱形具有而矩形不具有的性质是两条对角线互相垂直,
故选:A.
4.解:连接OP,如图所示:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OD=BD,AC=BD,
∴OA=OD,
BD===5,
∴OA=OD=,
∵△OAP的面积+△ODP的面积=△AOD的面积=矩形ABCD的面积,
即OA?PF+OD?PE=OA(PF+PE)=AB?AD=×4×3=3,
(PE+PF)=6
∴PE+PF==2.4,
故选:C.
5.解:∵∠B+∠C=180°,
∴AB∥DC,
∵∠A=∠C,
∴∠B+∠A=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴A不符合题意;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形,
∴B不符合题意;
∵∠A=∠B=90°,
∴∠A+∠B=180°,
∴AD∥BC,如图所示:
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形,
∴C不符合题意;
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,
∴D符合题意;
故选:A.
6.解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC,
∵AP=CQ,
∴AD﹣AP=BC﹣CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=6,连接PE,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∵BE=2AB=12,BC=AD=5,
∴CE==13.
∴PC+PB的最小值为13.
故选:D.
7.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
8.解:∵E是OC的中点,BE⊥AC,
∴直线BE是线段OC的垂直平分线,
∴BO=BC,
∵四边形ABCD为矩形,
∴BO=CO,
∴BO=BC=CO,
∴△OBC为等边三角形,
∴∠CBO=60°,
∵四边形ABCD为矩形,
∴AO=BO,∠ABC=∠DAB=90°,
∵OF⊥AB,
∴AF=BF,
∴OF为△BAD的中位线,
∴AD=2OF=8,
在Rt△BAD中,∠DBA=90°﹣60°=30°,
∴BD=2AD=16.
故选:A.
9.解:如图所示:
∵四边形ABCD和四边形③是矩形,
∴AB=CD,FP=CG,
∵AE=CG,
∴BE=DG,
∴阴影部分的面积=△BFD的面积﹣△BFP的面积=BF×CD﹣BF×FP=BF×(CD﹣CG)=BF×DG=BF×BE=矩形②面积,
故选:B.
10.解:这个条件可以是AE=AF,
理由:∵四边形ABCD是矩形,
∴AD∥BC,
即AF∥CE,
∵AF=EC,
∴四边形ABCD是平行四边形,
∵AE=AF,
∴四边形AECF是菱形,
故答案为:AE=AF.
11.解:如图,
∵四边形ABCD是矩形
∴AD∥BC,
∴∠AEB=∠EBC
又∵BE平分∠ABC,即∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE.
当AE=3cm,DE=5cm时,AD=BC=8cm,AB=CD=AE=3cm.
∴矩形ABCD的面积是:3×8=24cm2;
当AE=5cm,DE=3cm时,AD=BC=8cm,AB=CD=AE=5cm,
∴矩形ABCD的面积是:5×8=40cm2;
故答案为:24cm2或40cm2.
12.解:连接PC.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,
∴AB=5,
∴AC?BC=AB?PC,
∴PC=.
∴线段EF长的最小值为;
故答案为:.
13.解:∵CE∥BD,BE∥AC,
∴四边形OBEC是平行四边形,
∵四边形ABCD是菱形,
∴OC=OA=AC=12,OB=OD=BD=5,AC⊥BD,
∴∠BOC=90°,
∴BC===13,
∵四边形OBEC是平行四边形,
∴平行四边形OBEC是矩形,
∴OE=BC=13,
故答案为:13.
14.解:①当∠CFP=90°时,
∵△PCF为直角三角形,
∴∠CFP=90°,
∴∠CFD+∠PFA=90°,
∵四边形ABCD为矩形,
∴∠CAB+∠PAF=90°,
∵PE⊥AD,点A与点F关于PE对称,
∴PE=PA,EF=EA,
∴∠PFA=∠PAF,
∴∠CAB=∠CFD,
在△CBA和△CDF中
∴△CBA∽△CDF,
∴,
∵AB=CD=6,BC=8,
∴,
即DF=,
∴AE=(AD﹣DF)
=(8﹣)
=.
②当∠PCF=90°时,
∵∠ACB=∠CAF,∠B=∠ACF=90°,
∴△ACB∽△FAC,
∴=,
∴AF=,
∴AE=AF=
故答案为:或.
15.(1)证明:∵EF是AC的垂直平分线,
∴EF⊥AC,AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△EAO和△FCO中
,
∴△EAO≌△FCO(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF为平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形;
(2)解:∵四边形AECF为菱形,
∴AF=CF,
设AF=CF=x,
∵四边形ABCD是矩形,
∴∠B=90°,
由勾股定理得:AB2+BF2=AF2,
即42+(8﹣x)2=x2,
解得:x=5,
即CF=AF=5,
∵AB=4,
∴菱形AECF的面积S=CF×AB=5×4=20.
16.证明:∵AD、AE分别是∠BAC和∠BAF和外角的平分线,
∴∠DAB=∠CAB,∠BAE=∠BAF,
∴∠DAE=∠DAB+∠BAE=(∠CAB+∠ABF)=×180°=90°,
∵AE⊥BE,
∴∠AEB=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形.
17.(1)证明:∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一),
∴∠AEC=90°,
∵E、F分别是BC、AD的中点,
∴AF=AD,EC=BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形),
又∵∠AEC=90°,
∴四边形AECF是矩形(有一个角是直角的平行四边形是矩形);
(2)在Rt△ABE中,AE=,
所以,S菱形ABCD=2×=2.
18.解:作CE⊥OD于E,如图所示:
则∠CED=90°=∠AOB,
∵A(﹣1,0),B(0,﹣),D(0,2),
∴OA=1,OB=,OD=2,
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠CDE=∠ABO,
在△CDE和△ABO中,
,
∴△CDE≌△ABO(AAS),
∴CE=AO=1,DE=OB=,
∴OE=OD﹣DE=2﹣=,
∴点C的坐标为(1,);
19.解:(1)证明:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
(2)∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=3.
∴在Rt△ABE中,AE===4.
20.(1)证明:∵E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∴OA﹣AE=OC﹣CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)解:点E,F在AC上运动过程中,以D、E、B、F为顶点的四边形能为矩形,理由如下:
分为两种情况:
①∵四边形DEBF是矩形,
∴BD=EF=12cm,
即AE=CF=0.5tcm,
则16﹣0.5t﹣0.5t=12,
解得:t=4;
②当E到F位置上,F到E位置上时,AE=AF=0.5tcm,
则0.5t﹣12+0.5t=16,
解得:t=28,
即当运动时间t为4s或28s时,以D、E、B、F为顶点的四边形是矩形
1.如图,在矩形ABCD中,∠AOB=120°,AD=3,则AC=( )
A.6
B.
C.5
D.
2.矩形的三个顶点坐标分别是(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),那么第四个顶点坐标是( )
A.(1,﹣4)
B.(﹣8,﹣4)
C.(1,﹣3)
D.(3,﹣4)
3.下列性质中菱形有矩形不一定具有的性质是( )
A.对角线互相垂直
B.对角线互相平分
C.对角线相等
D.既是轴对称图形又是中心对称图形
4.如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( )
A.5
B.2.5
C.2.4
D.3
5.在四边形ABCD中,AC,BD交于点O.在下列各组条件中,不能判定四边形ABCD为矩形的是( )
A.∠A=∠C,∠B+∠C=180°,AC⊥BD
B.AO=CO,BO=DO,∠A=90°
C.∠A=∠B=90°,AC=BD
D.AB=CD,AD=BC,AC=BD
6.如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )
A.10
B.11
C.12
D.13
7.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24
B.24
C.12
D.12
8.如图,矩形ABCD的对角线相交于点O,OF⊥AB,BE⊥AC,E是OC的中点,OF=4,则BD的长为( )
A.16
B.8
C.4
D.8
9.如图,已知大矩形ABCD由①②③④四个小矩形组成,其中AE=CG,则只需要知道其中一个小矩形的面积就可以求出图中阴影部分的面积,这个小矩形是( )
A.①
B.②
C.③
D.④
10.如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC.只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是
(写出一个即可).
11.若矩形的一条内角平分线分一边为3cm和5cm两部分,则矩形的面积为
.
12.如图,直角三角形ABC中,AC=4,BC=3,P为斜边AB上一动点,且PE⊥AC,PF⊥BC,垂足分别是E、F,则线段EF长度的最小值是
.
13.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE∥BD,BE∥AC,连接OE,则OE的长是
.
14.如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F,则线段EF的最小值为
.
15.在矩形ABCD中,连接AC,AC的垂直平分线交AC于点O,分别交AD、BC于点E、F,连接CE和AF.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形AECF的面积.
16.如图,AD、AE分别是△ABC的内角∠BAC和外角∠BAF的平分线,BE⊥AE,DA⊥BC.求证:四边形AEBD是矩形.
17.如图,已知菱形ABCD,AB=AC,E、F分别是BC,AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=2,求菱形的面积.
18.如图,在直角坐标系中,?ABCD的顶点A,B,D的坐标是A(﹣1,0),B(0,﹣),D(0,2).求点C的坐标;
19.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连接AC.
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
20.如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度(AE=CF)向C、A运动,其速度为0.5cm/s.
(1)当E与F不重合时,求证:四边形DEBF是平行四边形;
(2)点E,F在AC上运动过程中,求当运动时间t为何值时,以D、E、B、F为顶点的四边形是矩形.
参考答案
1.解:∵∠AOB=120°,
∴∠AOD=60°,
∵矩形对角线相等且互相平分,
∴AO=DO,
∴△ADO为等边三角形,
∴AO=AD,AC=2AO=2AD=6.
故选:A.
2.解:如图所示:
∵矩形ABCD中,A、B、D三点的坐标分别(﹣2,﹣3),(1,﹣3),(﹣2,﹣4),
∴点C的横坐标与B的横坐标相等,纵坐标与D的纵坐标相等,
即C的坐标是(1,﹣4).
故选:A.
3.解:菱形的对角线互相平分、垂直、对角线平分一组对角,
矩形的对角线互相平分、相等,
故菱形具有而矩形不具有的性质是两条对角线互相垂直,
故选:A.
4.解:连接OP,如图所示:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OD=BD,AC=BD,
∴OA=OD,
BD===5,
∴OA=OD=,
∵△OAP的面积+△ODP的面积=△AOD的面积=矩形ABCD的面积,
即OA?PF+OD?PE=OA(PF+PE)=AB?AD=×4×3=3,
(PE+PF)=6
∴PE+PF==2.4,
故选:C.
5.解:∵∠B+∠C=180°,
∴AB∥DC,
∵∠A=∠C,
∴∠B+∠A=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴A不符合题意;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形,
∴B不符合题意;
∵∠A=∠B=90°,
∴∠A+∠B=180°,
∴AD∥BC,如图所示:
在Rt△ABC和Rt△BAD中,
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形,
∴C不符合题意;
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,
∴D符合题意;
故选:A.
6.解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC,
∵AP=CQ,
∴AD﹣AP=BC﹣CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=6,连接PE,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∵BE=2AB=12,BC=AD=5,
∴CE==13.
∴PC+PB的最小值为13.
故选:D.
7.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
8.解:∵E是OC的中点,BE⊥AC,
∴直线BE是线段OC的垂直平分线,
∴BO=BC,
∵四边形ABCD为矩形,
∴BO=CO,
∴BO=BC=CO,
∴△OBC为等边三角形,
∴∠CBO=60°,
∵四边形ABCD为矩形,
∴AO=BO,∠ABC=∠DAB=90°,
∵OF⊥AB,
∴AF=BF,
∴OF为△BAD的中位线,
∴AD=2OF=8,
在Rt△BAD中,∠DBA=90°﹣60°=30°,
∴BD=2AD=16.
故选:A.
9.解:如图所示:
∵四边形ABCD和四边形③是矩形,
∴AB=CD,FP=CG,
∵AE=CG,
∴BE=DG,
∴阴影部分的面积=△BFD的面积﹣△BFP的面积=BF×CD﹣BF×FP=BF×(CD﹣CG)=BF×DG=BF×BE=矩形②面积,
故选:B.
10.解:这个条件可以是AE=AF,
理由:∵四边形ABCD是矩形,
∴AD∥BC,
即AF∥CE,
∵AF=EC,
∴四边形ABCD是平行四边形,
∵AE=AF,
∴四边形AECF是菱形,
故答案为:AE=AF.
11.解:如图,
∵四边形ABCD是矩形
∴AD∥BC,
∴∠AEB=∠EBC
又∵BE平分∠ABC,即∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE.
当AE=3cm,DE=5cm时,AD=BC=8cm,AB=CD=AE=3cm.
∴矩形ABCD的面积是:3×8=24cm2;
当AE=5cm,DE=3cm时,AD=BC=8cm,AB=CD=AE=5cm,
∴矩形ABCD的面积是:5×8=40cm2;
故答案为:24cm2或40cm2.
12.解:连接PC.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,
∴AB=5,
∴AC?BC=AB?PC,
∴PC=.
∴线段EF长的最小值为;
故答案为:.
13.解:∵CE∥BD,BE∥AC,
∴四边形OBEC是平行四边形,
∵四边形ABCD是菱形,
∴OC=OA=AC=12,OB=OD=BD=5,AC⊥BD,
∴∠BOC=90°,
∴BC===13,
∵四边形OBEC是平行四边形,
∴平行四边形OBEC是矩形,
∴OE=BC=13,
故答案为:13.
14.解:①当∠CFP=90°时,
∵△PCF为直角三角形,
∴∠CFP=90°,
∴∠CFD+∠PFA=90°,
∵四边形ABCD为矩形,
∴∠CAB+∠PAF=90°,
∵PE⊥AD,点A与点F关于PE对称,
∴PE=PA,EF=EA,
∴∠PFA=∠PAF,
∴∠CAB=∠CFD,
在△CBA和△CDF中
∴△CBA∽△CDF,
∴,
∵AB=CD=6,BC=8,
∴,
即DF=,
∴AE=(AD﹣DF)
=(8﹣)
=.
②当∠PCF=90°时,
∵∠ACB=∠CAF,∠B=∠ACF=90°,
∴△ACB∽△FAC,
∴=,
∴AF=,
∴AE=AF=
故答案为:或.
15.(1)证明:∵EF是AC的垂直平分线,
∴EF⊥AC,AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△EAO和△FCO中
,
∴△EAO≌△FCO(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF为平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形;
(2)解:∵四边形AECF为菱形,
∴AF=CF,
设AF=CF=x,
∵四边形ABCD是矩形,
∴∠B=90°,
由勾股定理得:AB2+BF2=AF2,
即42+(8﹣x)2=x2,
解得:x=5,
即CF=AF=5,
∵AB=4,
∴菱形AECF的面积S=CF×AB=5×4=20.
16.证明:∵AD、AE分别是∠BAC和∠BAF和外角的平分线,
∴∠DAB=∠CAB,∠BAE=∠BAF,
∴∠DAE=∠DAB+∠BAE=(∠CAB+∠ABF)=×180°=90°,
∵AE⊥BE,
∴∠AEB=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形.
17.(1)证明:∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一),
∴∠AEC=90°,
∵E、F分别是BC、AD的中点,
∴AF=AD,EC=BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形),
又∵∠AEC=90°,
∴四边形AECF是矩形(有一个角是直角的平行四边形是矩形);
(2)在Rt△ABE中,AE=,
所以,S菱形ABCD=2×=2.
18.解:作CE⊥OD于E,如图所示:
则∠CED=90°=∠AOB,
∵A(﹣1,0),B(0,﹣),D(0,2),
∴OA=1,OB=,OD=2,
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠CDE=∠ABO,
在△CDE和△ABO中,
,
∴△CDE≌△ABO(AAS),
∴CE=AO=1,DE=OB=,
∴OE=OD﹣DE=2﹣=,
∴点C的坐标为(1,);
19.解:(1)证明:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
(2)∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=3.
∴在Rt△ABE中,AE===4.
20.(1)证明:∵E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∴OA﹣AE=OC﹣CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)解:点E,F在AC上运动过程中,以D、E、B、F为顶点的四边形能为矩形,理由如下:
分为两种情况:
①∵四边形DEBF是矩形,
∴BD=EF=12cm,
即AE=CF=0.5tcm,
则16﹣0.5t﹣0.5t=12,
解得:t=4;
②当E到F位置上,F到E位置上时,AE=AF=0.5tcm,
则0.5t﹣12+0.5t=16,
解得:t=28,
即当运动时间t为4s或28s时,以D、E、B、F为顶点的四边形是矩形
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
