高一数学任意角和弧度制及任意角的三角函数
文档属性
| 名称 | 高一数学任意角和弧度制及任意角的三角函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 245.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-05 00:00:00 | ||
图片预览










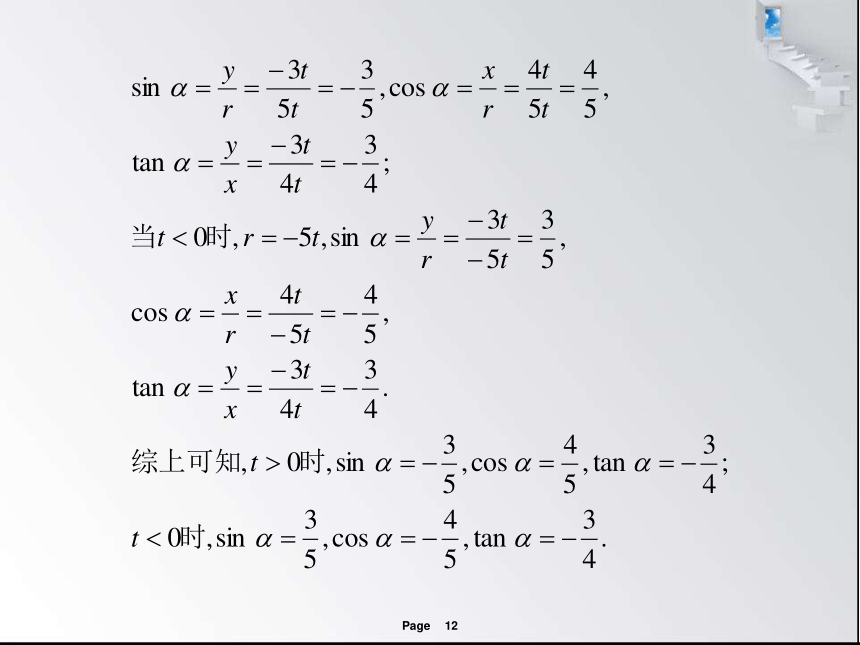
文档简介
(共44张PPT)
要点梳理
1.任意角
(1)角的概念的推广
①按旋转方向不同分为 、 、 .
②按终边位置不同分为 和 .
(2)终边相同的角
终边与角 相同的角可写成 .
第四编 三角函数、解三角形
§4.1 任意角和弧度制及任意角的三
角函数
正角
负角
零角
象限角
轴线角
(k∈Z)
基础知识 自主学习
(3)弧度制
①1弧度的角:_______________________________
叫做1弧度的角.
②规定:正角的弧度数为 ,负角的弧度数为
,零角的弧度数为 , ,l是以角
作为圆心角时所对圆弧的长,r为半径.
③用“弧度”做单位来度量角的制度叫做弧度制.比值 与所取的r的大小 ,仅与 .
④弧度与角度的换算:360°= 弧度;180°=
弧度.
⑤弧长公式: ,
扇形面积公式:S扇形= = .
把长度等于半径长的弧所对的圆心角
无关
角的大小有关
正数
负数
零
2.任意角的三角函数
(1)任意角的三角函数定义
设 是一个任意角,角 的终边上任意一点
P(x,y),它与原点的距离为r (r>0),那么角
的正弦、余弦、正切分别是:
它们都是以角为自
,以比值为 的函数.
(2)三角函数在各象限内的符号口诀是:
.
,
,
,
变量
函数值
一全
正、二正弦、三正切、四余弦
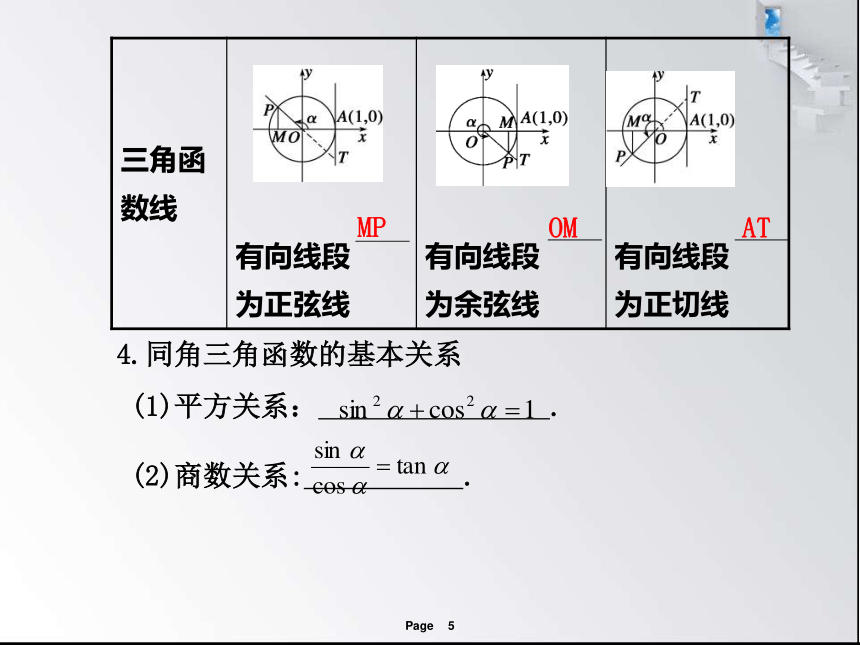
3.三角函数线
设角 的顶点在坐标原点,始边与x轴正半轴重
合,终边与单位圆相交于点P,过P作PM垂直于x
轴于M,则点M是点P在x轴上的 .由三角
函数的定义知,点P的坐标为 ,
即 ,其中 = ,
单位圆与x轴的正半轴交于点A,单位圆在A点
的切线与 的终边或其反向延长线相交于点
T,则 .我们把有向线段OM、
MP、AT叫做 的 、 、 .
OM
,
MP
AT
余弦线
正弦线
正切线
正射影
4.同角三角函数的基本关系
(1)平方关系: .
(2)商数关系: .
三角函
数线
有向线段
为正弦线
有向线段
为余弦线
有向线段
为正切线
MP
OM
AT
基础自测
1.若 =k·180°+45° (k∈Z),则 在( )
A.第一或第三象限 B.第一或第二象限
C.第二或第四象限 D.第三或第四象限
解析 当k=2m+1 (m∈Z)时,
=2m·180°+225°=m·360°+225°,故 为
第三象限角;当k=2m (m∈Z)时,
=m·360°+45°,故 为第一象限角.
A
2.角 终边过点(-1,2),则cos 等于( )
解析
C
3.已知角 的终边经过点( ,-1),则角 的最
小正值是( )
解析
B
4.已知扇形的周长是6 cm,面积是2 cm2,则扇形
的圆心角的弧度数是( )
A.1 B.4 C.1或4 D.2或4
解析 设此扇形的半径为r,弧长为l,
C
5.已知 为第四象限角,且
解 ∵ 为第四象限角,且
题型一 三角函数的定义
已知角 的终边在直线3x+4y=0上,求
的值.
本题求 的三角函数值.依据三角函
数的定义,可在角 的终边上任取一点P(4t,-3t)
(t≠0),求出r,由定义得出结论.
思维启迪
【例1】
解
题型分类 深度剖析
某角的三角函数值只与该角终边所在
位置有关,当终边确定时三角函数值就相应确定.
但若终边落在某条直线上时,这时终边实际上有
两个,因此对应的函数值有两组要分别求解.
知能迁移1 设 为第四象限角,其终边上的一个
点是P(x,- ),且
解 ∵ 为第四象限角,∴x>0,且
题型二 三角函数值的符号及判定
(1)如果点P(sin ·cos ,2cos )位
于第三象限,试判断角 所在的象限.
(2)若 是第二象限角,试判断 的符
号.
(1)由点P所在的象限可知
的符号,进而判断 所在的象限.
(2)由 可判断 的范围,把
看作一个角,再判断
的符号.
解
(1)熟练掌握三角函数的符号法则是
解决此类问题的关键.
(2)由三角函数符号判断角所在象限,在写角的
集合时,注意终边相同的角.
知能迁移2 若 则
角 的终边落在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析
C
题型三 三角函数线及其应用
在单位圆中画出适合下列条件的角 的
终边的范围,并由此写出角 的集合:
作出满足
的角的终边,然后根据已知条件确定角 终边的
范围.
解 (1)作直线 交单位圆于A、B
两点,连结OA、OB,则OA与OB围
成的区域即为角 的终边的范围,
故满足条件的角 的集合为
(2)作直线 交单位圆于C、D两点,
连结OC、OD,则OC与OD围成的区域
(图中阴影部分)即为角 终边的范围.
故满足条件的角 的集合为
本题的实质是解三角不等式的问题:
(1)可以运用单位圆及三角函数线;
(2)也可以用三角函数图象.
体现了数形结合的数学思想方法.
知能迁移3 求下列函数的定义域:
解
由三角函数线画出x满足条件的终边
范围(如图阴影所示).
利用三角函数线画出x满足条件的终边范围(如右图阴影),
题型四 同角三角函数的基本关系式
(12分)已知 是三角形的内角,且
(1)求tan 的值;
(2) 用tan 表示出来,并求其值.
(1)由
解 (1)方法一
2分
3分
6分
方法二
3分
6分
(1)对于
这三个式子,已知其中一个式子的值,其余二式的
值可求.转化的公式为
(2)关于sin x,cos x的齐次式,往往化为关于
tan x的式子.
10分
12分
知能迁移4 分别求 的值:
解
思想方法 感悟提高
方法与技巧
1.在利用三角函数定义时,点P可取终边上任一点,
如有可能则取终边与单位圆的交点.|OP|=r一定
是正值.
2.在解决 的问题时,常
常用到
3.在解简单的三角不等式时,利用单位圆及三角
函数线是一个小技巧.
失误与防范
1.注意易混概念的区别:第一象限角、锐角、小
于90°的角是概念不同的三类角.第一类是象
限角,第二、第三类是区间角.
2.角度制与弧度制可利用180°= rad进行互化,
在同一个式子中,采用的度量制度必须一致,
不可混用.
3.注意熟记0°~360°间特殊角的弧度表示.
一、选择题
1.若角 和角 的终边关于x轴对称,则角 可以用
角 表示为 ( )
A. (k∈Z) B. (k∈Z)
C. (k∈Z) D. (k∈Z)
解析 因为角 和角 的终边关于x轴对称,所
以 (k∈Z).所以 (k∈Z).
定时检测
B
2.已知点P 在第三象限,则角 的终边在
第几象限 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ∵P 在第三象限,
由tan <0,得 在第二、四象限,
由cos <0,得 在第二、三象限,
∴ 在第二象限.
B
3.若扇形圆心角的弧度数为2,且扇形弧所对的弦长
也是2,则这个扇形的面积为 ( )
解析 由题意得扇形的半径为 又由扇形面
积公式得,该扇形的面积为
A
4.已知角 的终边过点P(-8m,-6sin 30°),且
则m的值为 ( )
解析
B
5.已知角 是第二象限角,且 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
解析 由 是第二象限角知, 是第一或第三
象限角.
C
6.已知 是第一象限角, 等于( )
解析
B
二、填空题
7.若点P(m,n)(n≠0)为角600°终边上一点,则
等于 .
解析 由三角函数的定义知
8.已知P在1秒钟内转过的角度为θ(0°<θ<180°),
经过2秒钟达到第三象限,经过14秒钟后又恰好回到
出发点,则θ = .
解析 ∵0°<θ<180°且
k·360°+180°<2θ则必有k=0,于是90°<θ<135°,
又14θ=n·360°(n∈Z),
9.若角 的终边落在直线y=-x上,则
的值等于 .
解析
∵角 的终边落在直线y=-x上,
∴角 是第二或第四象限角.
0
三、解答题
10.角 终边上的点P与A(a,2a)关于x轴对称(a≠0),
角 终边上的点Q与A关于直线y=x 对称,求
的值.
解 由题意得,点P的坐标为(a,-2a),
点Q的坐标为(2a,a).
11.设 为第三象限角,试判断
解
12. 求下列各式的值:
解 由已知得
返回
要点梳理
1.任意角
(1)角的概念的推广
①按旋转方向不同分为 、 、 .
②按终边位置不同分为 和 .
(2)终边相同的角
终边与角 相同的角可写成 .
第四编 三角函数、解三角形
§4.1 任意角和弧度制及任意角的三
角函数
正角
负角
零角
象限角
轴线角
(k∈Z)
基础知识 自主学习
(3)弧度制
①1弧度的角:_______________________________
叫做1弧度的角.
②规定:正角的弧度数为 ,负角的弧度数为
,零角的弧度数为 , ,l是以角
作为圆心角时所对圆弧的长,r为半径.
③用“弧度”做单位来度量角的制度叫做弧度制.比值 与所取的r的大小 ,仅与 .
④弧度与角度的换算:360°= 弧度;180°=
弧度.
⑤弧长公式: ,
扇形面积公式:S扇形= = .
把长度等于半径长的弧所对的圆心角
无关
角的大小有关
正数
负数
零
2.任意角的三角函数
(1)任意角的三角函数定义
设 是一个任意角,角 的终边上任意一点
P(x,y),它与原点的距离为r (r>0),那么角
的正弦、余弦、正切分别是:
它们都是以角为自
,以比值为 的函数.
(2)三角函数在各象限内的符号口诀是:
.
,
,
,
变量
函数值
一全
正、二正弦、三正切、四余弦
3.三角函数线
设角 的顶点在坐标原点,始边与x轴正半轴重
合,终边与单位圆相交于点P,过P作PM垂直于x
轴于M,则点M是点P在x轴上的 .由三角
函数的定义知,点P的坐标为 ,
即 ,其中 = ,
单位圆与x轴的正半轴交于点A,单位圆在A点
的切线与 的终边或其反向延长线相交于点
T,则 .我们把有向线段OM、
MP、AT叫做 的 、 、 .
OM
,
MP
AT
余弦线
正弦线
正切线
正射影
4.同角三角函数的基本关系
(1)平方关系: .
(2)商数关系: .
三角函
数线
有向线段
为正弦线
有向线段
为余弦线
有向线段
为正切线
MP
OM
AT
基础自测
1.若 =k·180°+45° (k∈Z),则 在( )
A.第一或第三象限 B.第一或第二象限
C.第二或第四象限 D.第三或第四象限
解析 当k=2m+1 (m∈Z)时,
=2m·180°+225°=m·360°+225°,故 为
第三象限角;当k=2m (m∈Z)时,
=m·360°+45°,故 为第一象限角.
A
2.角 终边过点(-1,2),则cos 等于( )
解析
C
3.已知角 的终边经过点( ,-1),则角 的最
小正值是( )
解析
B
4.已知扇形的周长是6 cm,面积是2 cm2,则扇形
的圆心角的弧度数是( )
A.1 B.4 C.1或4 D.2或4
解析 设此扇形的半径为r,弧长为l,
C
5.已知 为第四象限角,且
解 ∵ 为第四象限角,且
题型一 三角函数的定义
已知角 的终边在直线3x+4y=0上,求
的值.
本题求 的三角函数值.依据三角函
数的定义,可在角 的终边上任取一点P(4t,-3t)
(t≠0),求出r,由定义得出结论.
思维启迪
【例1】
解
题型分类 深度剖析
某角的三角函数值只与该角终边所在
位置有关,当终边确定时三角函数值就相应确定.
但若终边落在某条直线上时,这时终边实际上有
两个,因此对应的函数值有两组要分别求解.
知能迁移1 设 为第四象限角,其终边上的一个
点是P(x,- ),且
解 ∵ 为第四象限角,∴x>0,且
题型二 三角函数值的符号及判定
(1)如果点P(sin ·cos ,2cos )位
于第三象限,试判断角 所在的象限.
(2)若 是第二象限角,试判断 的符
号.
(1)由点P所在的象限可知
的符号,进而判断 所在的象限.
(2)由 可判断 的范围,把
看作一个角,再判断
的符号.
解
(1)熟练掌握三角函数的符号法则是
解决此类问题的关键.
(2)由三角函数符号判断角所在象限,在写角的
集合时,注意终边相同的角.
知能迁移2 若 则
角 的终边落在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析
C
题型三 三角函数线及其应用
在单位圆中画出适合下列条件的角 的
终边的范围,并由此写出角 的集合:
作出满足
的角的终边,然后根据已知条件确定角 终边的
范围.
解 (1)作直线 交单位圆于A、B
两点,连结OA、OB,则OA与OB围
成的区域即为角 的终边的范围,
故满足条件的角 的集合为
(2)作直线 交单位圆于C、D两点,
连结OC、OD,则OC与OD围成的区域
(图中阴影部分)即为角 终边的范围.
故满足条件的角 的集合为
本题的实质是解三角不等式的问题:
(1)可以运用单位圆及三角函数线;
(2)也可以用三角函数图象.
体现了数形结合的数学思想方法.
知能迁移3 求下列函数的定义域:
解
由三角函数线画出x满足条件的终边
范围(如图阴影所示).
利用三角函数线画出x满足条件的终边范围(如右图阴影),
题型四 同角三角函数的基本关系式
(12分)已知 是三角形的内角,且
(1)求tan 的值;
(2) 用tan 表示出来,并求其值.
(1)由
解 (1)方法一
2分
3分
6分
方法二
3分
6分
(1)对于
这三个式子,已知其中一个式子的值,其余二式的
值可求.转化的公式为
(2)关于sin x,cos x的齐次式,往往化为关于
tan x的式子.
10分
12分
知能迁移4 分别求 的值:
解
思想方法 感悟提高
方法与技巧
1.在利用三角函数定义时,点P可取终边上任一点,
如有可能则取终边与单位圆的交点.|OP|=r一定
是正值.
2.在解决 的问题时,常
常用到
3.在解简单的三角不等式时,利用单位圆及三角
函数线是一个小技巧.
失误与防范
1.注意易混概念的区别:第一象限角、锐角、小
于90°的角是概念不同的三类角.第一类是象
限角,第二、第三类是区间角.
2.角度制与弧度制可利用180°= rad进行互化,
在同一个式子中,采用的度量制度必须一致,
不可混用.
3.注意熟记0°~360°间特殊角的弧度表示.
一、选择题
1.若角 和角 的终边关于x轴对称,则角 可以用
角 表示为 ( )
A. (k∈Z) B. (k∈Z)
C. (k∈Z) D. (k∈Z)
解析 因为角 和角 的终边关于x轴对称,所
以 (k∈Z).所以 (k∈Z).
定时检测
B
2.已知点P 在第三象限,则角 的终边在
第几象限 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ∵P 在第三象限,
由tan <0,得 在第二、四象限,
由cos <0,得 在第二、三象限,
∴ 在第二象限.
B
3.若扇形圆心角的弧度数为2,且扇形弧所对的弦长
也是2,则这个扇形的面积为 ( )
解析 由题意得扇形的半径为 又由扇形面
积公式得,该扇形的面积为
A
4.已知角 的终边过点P(-8m,-6sin 30°),且
则m的值为 ( )
解析
B
5.已知角 是第二象限角,且 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
解析 由 是第二象限角知, 是第一或第三
象限角.
C
6.已知 是第一象限角, 等于( )
解析
B
二、填空题
7.若点P(m,n)(n≠0)为角600°终边上一点,则
等于 .
解析 由三角函数的定义知
8.已知P在1秒钟内转过的角度为θ(0°<θ<180°),
经过2秒钟达到第三象限,经过14秒钟后又恰好回到
出发点,则θ = .
解析 ∵0°<θ<180°且
k·360°+180°<2θ
又14θ=n·360°(n∈Z),
9.若角 的终边落在直线y=-x上,则
的值等于 .
解析
∵角 的终边落在直线y=-x上,
∴角 是第二或第四象限角.
0
三、解答题
10.角 终边上的点P与A(a,2a)关于x轴对称(a≠0),
角 终边上的点Q与A关于直线y=x 对称,求
的值.
解 由题意得,点P的坐标为(a,-2a),
点Q的坐标为(2a,a).
11.设 为第三象限角,试判断
解
12. 求下列各式的值:
解 由已知得
返回
