11.1.2三角形的高、中线与角平分线暑期学情跟踪练习 2021—2022学年人教版数学八年级上册(word版含答案)
文档属性
| 名称 | 11.1.2三角形的高、中线与角平分线暑期学情跟踪练习 2021—2022学年人教版数学八年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 19:29:48 | ||
图片预览


文档简介
11.1.2三角形的高、中线与角平分线暑期学情跟踪练习
一、选择题
1.三角形的重心是指(
)
A.三个内角平分线的交点
B.三边上的高的交点
C.三条中线的交点
D.三边垂直平分线的交点
2.在△ABC中,D是BC上的一点,且△ABD的面积与△ADC的面积相等,则线段AD为△ABC的(???
).
A.高??
???
B.角平分线??
????
C.中线?
???????
D.不能确定
3.如图
AD⊥BC
于
D,GC⊥BC
于
C,CF⊥AB
于
F,图中是△ABC
的高的线段有(
).
A.1
条
B.2
条
C.3
条
D.4
条
4.如图,AM是△ABC的中线,△ABC的面积为2acm2,则△AMC面积为(???)
A.4acm2
?B.2acm2?
C.acm2
????
D.以上答案都不正确
5.如图,的中线、相交于点F,下列结论正确的有(
)
①S△ABD=S△DCA;②S△AEF=S△BDF;③S四边形EFDC=3S△AEF;④S△ABC=S△ABF.
A.1个
B.2个
C.3个
D.4个
6.已知是△ABC的中线,,,且的周长为11,则的周长是(
)
A.14
B.9
C.16
D.不能确定
7.能将三角形面积平分的是三角形的(
)
A.角平分线
B.高
C.中线
D.外角平分线
8.如图,在中,是高,是中线,是角平分线,交于点,交于点,下面说法①的面积的面积;②;③;④正确的是(
)
A.①②③④
B.①②③
C.①②④
D.③④
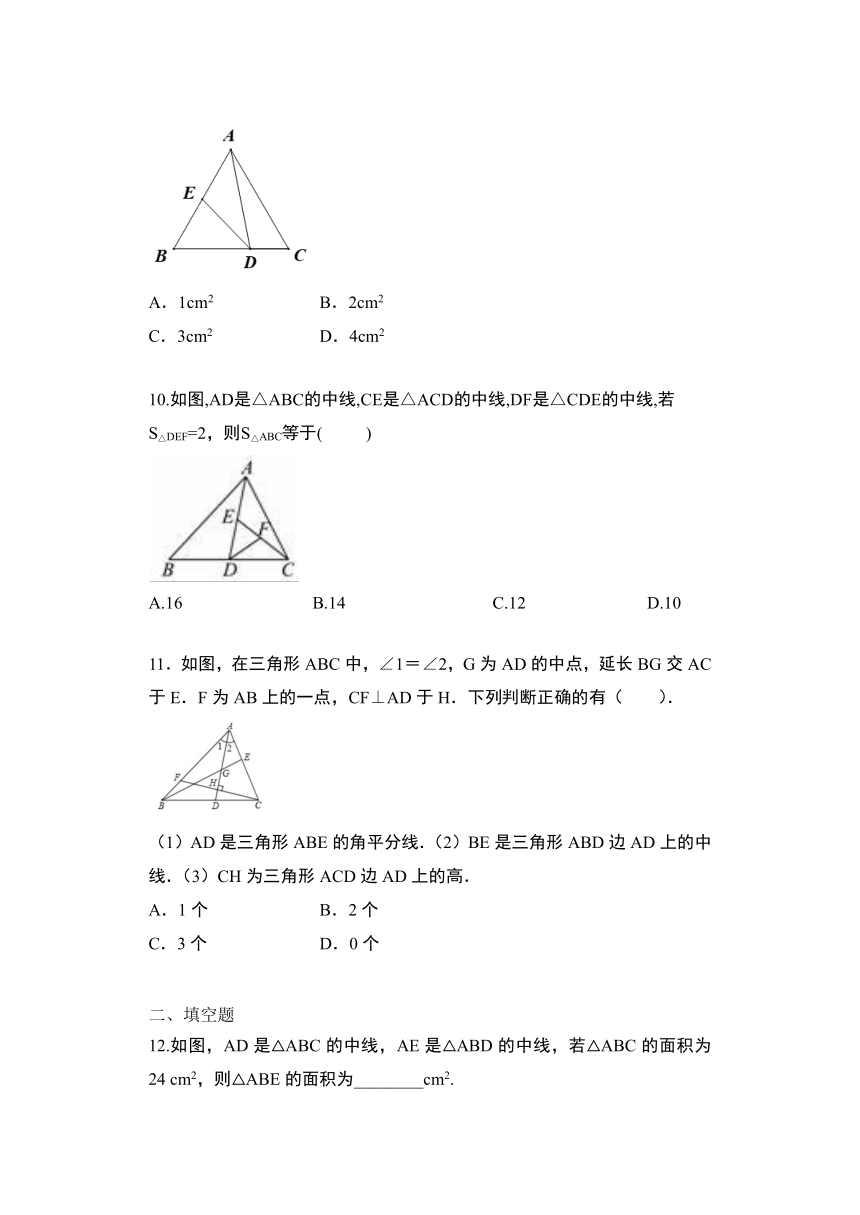
9.如图,在△中,已知,点是的中点,且△的面积为9cm2,则△的面积为(
)
A.1cm2
B.2cm2
C.3cm2
D.4cm2
10.如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=2,则S△ABC等于(
)
A.16
B.14
C.12
D.10
11.如图,在三角形ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有(??????
).
(1)AD是三角形ABE的角平分线.(2)BE是三角形ABD边AD上的中线.(3)CH为三角形ACD边AD上的高.
A.1个
B.2个
C.3个
D.0个
二、填空题
12.如图,AD是△ABC的中线,AE是△ABD的中线,若△ABC的面积为24
cm2,则△ABE的面积为________cm2.
13.如图,点O在△ABC内部,且OB平分∠ABC,OC平分∠ACB.且∠A=70°,则∠BOC=______°.
14.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=6,则S1﹣S2=___.
15.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为_____.
三、解答题
16.在△ABC中,AB=2BC,AD、CE分别是
BC、AB
边上的高,试判断
AD和
CE的大小关系,并说明理由.
17.如图,ADBC,,求三角形ABC与三角形ACD的面积之比.
18.已知等腰三角形一腰上的中线把这个三角形的周长分成
9cm和
15cm两部分,求这个三角形的腰长。
19.如图,BM是△ABC的中线,AB=5cm,BC=3cm,那么△ABM与△BCM的周长的差是多少?
20.如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到,图中标出了点B的对应点.根据下列条件利用网格点和三角板(或直尺)画图:
(1)补全△A`B`C`;
(2)画出△ABC中AB边上的中线CD;
(3)画出△ABC中BC边上的高线AE;
21.如图,已知长方形中,,,点是的中点,点从点出发在上以每秒1cm的速度向点运动,运动时间设为秒.(假定)
(1)当秒时,求阴影部分(即三角形)的面积;
(2)用含的式子表示阴影部分的面积;并求出当三角形的面积等于3时,阴影部分的面积是多少?
(3)过点作交于点,过点作交于点,请直接写出在点运动过程中,和的数量关系.
答案
一、选择题
1.
C
2.
C
3.
B
4.
C
5.
C
6.
B
7.
C
8.
B
9.
C
10.
A
11.
A
二、填空题
12.
6
13.
125
14.
1
15.
14°
三、解答题
16.
解:设BC=a
AB=2a
CE=c
AD=d
根据三角形面积相等可得:ad=2ac
化简得:d=2c
故:AD=2CE
17.
18.
解:设腰xcm,底边ycm。则
(1)x+x/2=9
x/2+y=15∴x=6
y=12∴2x=y∴舍去
(2)x+x/2=15.
x/2+y=9∴x=10
y=4∴2x>y∴符合
答:腰长10cm,底边4cm
19.
2cm.
20.
解:(1)先根据平移的特点找出,再顺次连接点即可得,如图所示:
(2)先找出AB边的中点,再连接CD即可得,如图所示:
(3)过点A作BC所在直线的垂线即为BC边上的高线AE,如图所示:
21.
(1);(2);;(3)
试卷第8页,总8页
一、选择题
1.三角形的重心是指(
)
A.三个内角平分线的交点
B.三边上的高的交点
C.三条中线的交点
D.三边垂直平分线的交点
2.在△ABC中,D是BC上的一点,且△ABD的面积与△ADC的面积相等,则线段AD为△ABC的(???
).
A.高??
???
B.角平分线??
????
C.中线?
???????
D.不能确定
3.如图
AD⊥BC
于
D,GC⊥BC
于
C,CF⊥AB
于
F,图中是△ABC
的高的线段有(
).
A.1
条
B.2
条
C.3
条
D.4
条
4.如图,AM是△ABC的中线,△ABC的面积为2acm2,则△AMC面积为(???)
A.4acm2
?B.2acm2?
C.acm2
????
D.以上答案都不正确
5.如图,的中线、相交于点F,下列结论正确的有(
)
①S△ABD=S△DCA;②S△AEF=S△BDF;③S四边形EFDC=3S△AEF;④S△ABC=S△ABF.
A.1个
B.2个
C.3个
D.4个
6.已知是△ABC的中线,,,且的周长为11,则的周长是(
)
A.14
B.9
C.16
D.不能确定
7.能将三角形面积平分的是三角形的(
)
A.角平分线
B.高
C.中线
D.外角平分线
8.如图,在中,是高,是中线,是角平分线,交于点,交于点,下面说法①的面积的面积;②;③;④正确的是(
)
A.①②③④
B.①②③
C.①②④
D.③④
9.如图,在△中,已知,点是的中点,且△的面积为9cm2,则△的面积为(
)
A.1cm2
B.2cm2
C.3cm2
D.4cm2
10.如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=2,则S△ABC等于(
)
A.16
B.14
C.12
D.10
11.如图,在三角形ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有(??????
).
(1)AD是三角形ABE的角平分线.(2)BE是三角形ABD边AD上的中线.(3)CH为三角形ACD边AD上的高.
A.1个
B.2个
C.3个
D.0个
二、填空题
12.如图,AD是△ABC的中线,AE是△ABD的中线,若△ABC的面积为24
cm2,则△ABE的面积为________cm2.
13.如图,点O在△ABC内部,且OB平分∠ABC,OC平分∠ACB.且∠A=70°,则∠BOC=______°.
14.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=6,则S1﹣S2=___.
15.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为_____.
三、解答题
16.在△ABC中,AB=2BC,AD、CE分别是
BC、AB
边上的高,试判断
AD和
CE的大小关系,并说明理由.
17.如图,ADBC,,求三角形ABC与三角形ACD的面积之比.
18.已知等腰三角形一腰上的中线把这个三角形的周长分成
9cm和
15cm两部分,求这个三角形的腰长。
19.如图,BM是△ABC的中线,AB=5cm,BC=3cm,那么△ABM与△BCM的周长的差是多少?
20.如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到,图中标出了点B的对应点.根据下列条件利用网格点和三角板(或直尺)画图:
(1)补全△A`B`C`;
(2)画出△ABC中AB边上的中线CD;
(3)画出△ABC中BC边上的高线AE;
21.如图,已知长方形中,,,点是的中点,点从点出发在上以每秒1cm的速度向点运动,运动时间设为秒.(假定)
(1)当秒时,求阴影部分(即三角形)的面积;
(2)用含的式子表示阴影部分的面积;并求出当三角形的面积等于3时,阴影部分的面积是多少?
(3)过点作交于点,过点作交于点,请直接写出在点运动过程中,和的数量关系.
答案
一、选择题
1.
C
2.
C
3.
B
4.
C
5.
C
6.
B
7.
C
8.
B
9.
C
10.
A
11.
A
二、填空题
12.
6
13.
125
14.
1
15.
14°
三、解答题
16.
解:设BC=a
AB=2a
CE=c
AD=d
根据三角形面积相等可得:ad=2ac
化简得:d=2c
故:AD=2CE
17.
18.
解:设腰xcm,底边ycm。则
(1)x+x/2=9
x/2+y=15∴x=6
y=12∴2x=y∴舍去
(2)x+x/2=15.
x/2+y=9∴x=10
y=4∴2x>y∴符合
答:腰长10cm,底边4cm
19.
2cm.
20.
解:(1)先根据平移的特点找出,再顺次连接点即可得,如图所示:
(2)先找出AB边的中点,再连接CD即可得,如图所示:
(3)过点A作BC所在直线的垂线即为BC边上的高线AE,如图所示:
21.
(1);(2);;(3)
试卷第8页,总8页
