山东省菏泽市某重点高中2012届高三下学期5月高考冲刺题 数学文
文档属性
| 名称 | 山东省菏泽市某重点高中2012届高三下学期5月高考冲刺题 数学文 |

|
|
| 格式 | zip | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-06 00:00:00 | ||
图片预览




文档简介
山东省菏泽市某重点高中2012届高三下学期5月高考冲刺题
文 科 数 学
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页,满分150分。考试用时120分钟。
参考公式:
柱体的体积公式:,其中表示柱体的底面积,表示柱体的高.
圆柱的侧面积公式:,其中c是圆柱的底面周长,是圆柱的母线长.
球的体积公式V=, 其中R是球的半径.
球的表面积公式:S=4π,其中R是球的半径.
用最小二乘法求线性回归方程系数公式 .
如果事件互斥,那么.
第I卷 (选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知全集,集合,,那么集合 ( )
A. B.
C. D.
2.已知复数,是z的共轭复数,则的模等于 ( )
A. B.2 C.1 D.
3.已知平面向量等于 ( )
A.9 B.1 C.-1 D.-9
4.设等差数列的前n项和为,若,,则当取最小值时,n等于
A.6 B.7 C.8 D.9
5.若不等式组所表示的平面区域被直线分为面积相等的两部分,则的值是 ( )A. B. C. D.
6.如果执行右面的框图,输入N=6,则输出的数等于 ( )
A. B.
C. D.
7.设偶函数满足(x0),则= ( )
A.
B.
C.
D.
8.甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,,分别表示甲乙两名运动员这项测试成绩的平均数,,分别表示甲乙两名运动员这项测试成绩的标准差,则有 ( )
A. B.
C. D.
9.已知a>0且a≠1,若函数f (x)= loga(ax2 –x)在[3,4]是增函数,则a的取值范围是( )
A.(1,+∞) B. C. D.
10.删去正整数数列1,2,3,……中的所有完全平方数,得到一个新数列,这个新数列的第2003项是 ( )
A.2048 B.2049 C.2050 D.2051
11.设函数,曲线处的切线方程为,则曲线处的切线方程为 ( )
A. B.
C. D.
12.已知为椭圆的两个焦点,P为椭圆上一点且,则此椭圆离心率的取值范围是 ( )
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题:(每小题4分,共16分,把正确答案填写在答卷相应的横线上)
13.设长方体的长、宽、高分别为2、、,其顶点都在一个球面上,则该球的表面积为 _________.
14.设函数的定义域为D,若存在非零数使得对于任意有且,则称为M上的高调函数。
现给出下列命题:
①函数为R上的1高调函数;
②函数为R上的高调函数
③如果定义域为的函数为上高调函数,那么实数的取值范围是
其中正确的命题是 。(写出所有正确命题的序号)
15.某人午休醒来,发觉表停了,他打开收音机想收听电台整点报时,则他等待的时间短于分钟的概率为 .
16.若直角坐标平面内两点P、Q满足条件:①P、Q都在函数的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数则的“友好点对”、
有 个.
三、解答题:(本大题共6小题,满分74分.解答须写出文字说明、证明过程和演算步骤)
17.(本小题满分12分)
已知函数(),相邻两条对称轴之间的距离等于.
(Ⅰ)求的值;
(Ⅱ)当时,求函数的最大值和最小值及相应的x值.
18.(本小题满分12分)
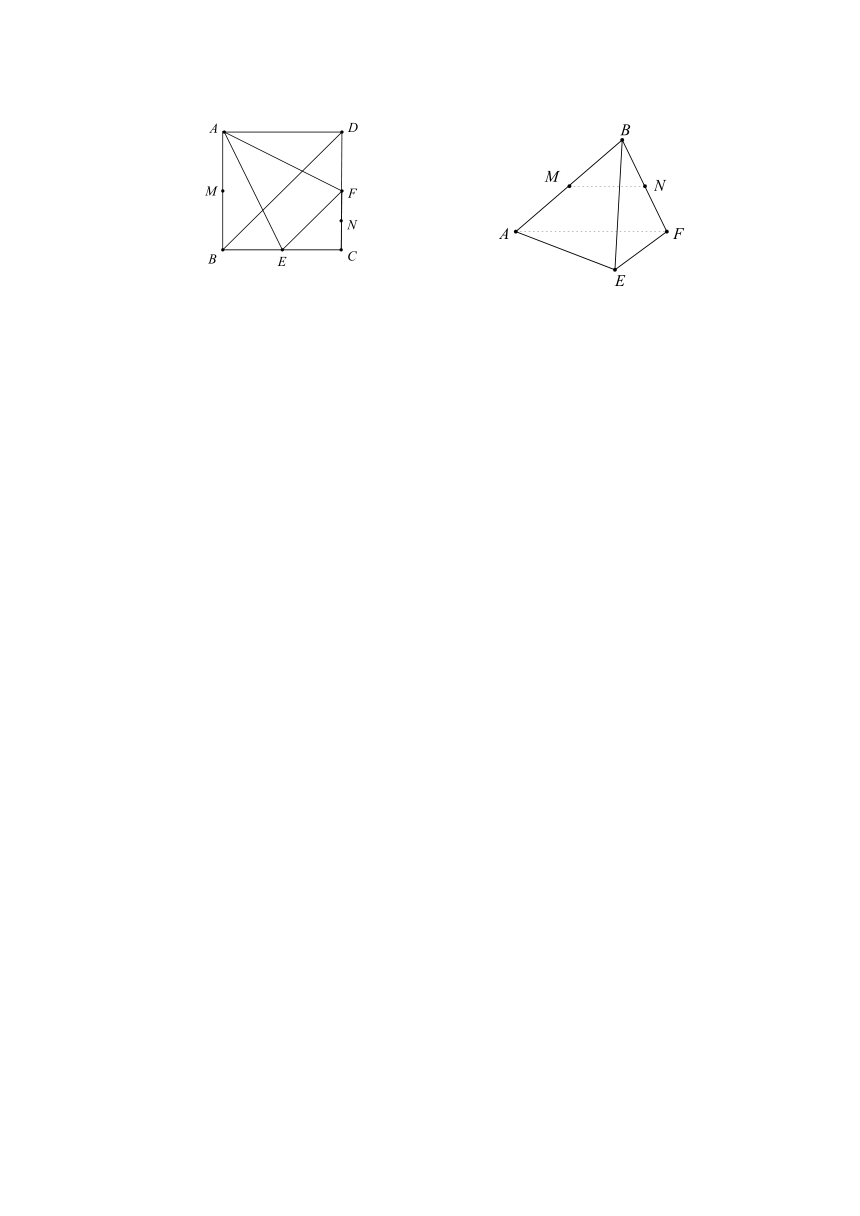
在边长为的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(I)判别MN与平面AEF的位置关系,并给出证明;
(II)求多面体E-AFMN的体积.
19.(本小题满分12分)
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男生身高频数分布表
身高(cm) [160,165) [165,170) [170,175) [175,180) [180,185) [185,190)
频数 2 5 14 13 4 2
表2:女生身高频数分布表
身高(cm) [150,155) [155,160) [160,165) [165,170) [170,175) [175,180)
频数 1 7 12 6 3 1
(I)求该校男生的人数并完成下面频率分布直方图;
(II)估计该校学生身高在的概率;
(III)从样本中身高在180190cm之间的男生中任选2人,求至少有1人身高在185190cm之间的概率。
20.(本小题满分12分)
设函数.
(I)求的单调区间;
(II)当021.(本小题满分12分)
已知点为圆上的动点,且不在轴上,轴,垂足为,线段中点的轨迹为曲线,过定点任作一条与轴不垂直的直线,它与曲线交于、两点。
(I)求曲线的方程;
(II)试证明:在轴上存在定点,使得总能被轴平分
22.(本小题满分14分)
已知点列满足:,其中,又已知,.
(I)若,求的表达式;
(II)已知点B,记,且成立,试求a的取值范围;
(III)设(2)中的数列的前n项和为,试求: 。
文科数学答案
1-5BCDAB 6-10DBBAA 11—12 BC
13.62 14.②③ 15. 16.2
17.(Ⅰ).
因为 ,所以 ,. ………………… 3分
所以 .
所以 ………………………7分
(Ⅱ)
当 时, , ………………………9分
所以 当,即时,, ………………11分
当,即时,. ………………………12分
18.(1)因翻折后B、C、D重合(如图),
所以MN应是的一条中位线,………………3分
则.………6分
(2)因为平面BEF,……………8分
且,
∴,………………………………………10分
又 ∴.…………………………………12分
19.(1)样本中男生人数为40 ,
由分层抽样比例为10%可得全校男生人数为400.----2分
频率分布直方图如右图示:---------------------------------------4分
(2)由表1、表2知,样本中身高在的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的频率-----------------------------------------6分
故由估计该校学生身高在的概率.--------------------8分
(3)样本中身高在180185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:
--10分
故从样本中身高在180190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185190cm之间的可能结果数为9,因此,所求概率.---------------12分
20.(I)定义域为. ………………………1分
.
令,则,所以或. ……………………3分
因为定义域为,所以.
令,则,所以.
因为定义域为,所以. ………………………5分
所以函数的单调递增区间为,
单调递减区间为. ………………………7分
(II) ().
.
因为0所以函数在上为减函数,在上为增函数.
①当,即时,
在区间上,在上为减函数,在上为增函数.
所以. ………………………10分
②当,即时,在区间上为减函数.
所以.
综上所述,当时,;
当时,. ………………12分
21.(1)设为曲线上的任意一点,则点在圆上,
∴,曲线的方程为. ………………2分
(2)设点的坐标为,直线的方程为, ………………3分
代入曲线的方程,可得 ,……5分
∵,∴,
∴直线与曲线总有两个公共点.(也可根据点M在椭圆的内部得到此结论)
………………6分
设点,的坐标分别, ,则,
要使被轴平分,只要, ………………9分
即,, ………………10分
也就是,,
即,即只要 ………………12分
当时,(*)对任意的s都成立,从而总能被轴平分.
所以在x轴上存在定点,使得总能被轴平分.
22.(1)∵,,∴,
∴,∴,∴. …3分
(2)∵,∴.
∵
∴要使成立,只要,即∴为所求. ……6分
(3)∵
,∴ ……9分
∴
………………11分
∵,∴,∴…13分∴ ……14分
文 科 数 学
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页,满分150分。考试用时120分钟。
参考公式:
柱体的体积公式:,其中表示柱体的底面积,表示柱体的高.
圆柱的侧面积公式:,其中c是圆柱的底面周长,是圆柱的母线长.
球的体积公式V=, 其中R是球的半径.
球的表面积公式:S=4π,其中R是球的半径.
用最小二乘法求线性回归方程系数公式 .
如果事件互斥,那么.
第I卷 (选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知全集,集合,,那么集合 ( )
A. B.
C. D.
2.已知复数,是z的共轭复数,则的模等于 ( )
A. B.2 C.1 D.
3.已知平面向量等于 ( )
A.9 B.1 C.-1 D.-9
4.设等差数列的前n项和为,若,,则当取最小值时,n等于
A.6 B.7 C.8 D.9
5.若不等式组所表示的平面区域被直线分为面积相等的两部分,则的值是 ( )A. B. C. D.
6.如果执行右面的框图,输入N=6,则输出的数等于 ( )
A. B.
C. D.
7.设偶函数满足(x0),则= ( )
A.
B.
C.
D.
8.甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,,分别表示甲乙两名运动员这项测试成绩的平均数,,分别表示甲乙两名运动员这项测试成绩的标准差,则有 ( )
A. B.
C. D.
9.已知a>0且a≠1,若函数f (x)= loga(ax2 –x)在[3,4]是增函数,则a的取值范围是( )
A.(1,+∞) B. C. D.
10.删去正整数数列1,2,3,……中的所有完全平方数,得到一个新数列,这个新数列的第2003项是 ( )
A.2048 B.2049 C.2050 D.2051
11.设函数,曲线处的切线方程为,则曲线处的切线方程为 ( )
A. B.
C. D.
12.已知为椭圆的两个焦点,P为椭圆上一点且,则此椭圆离心率的取值范围是 ( )
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题:(每小题4分,共16分,把正确答案填写在答卷相应的横线上)
13.设长方体的长、宽、高分别为2、、,其顶点都在一个球面上,则该球的表面积为 _________.
14.设函数的定义域为D,若存在非零数使得对于任意有且,则称为M上的高调函数。
现给出下列命题:
①函数为R上的1高调函数;
②函数为R上的高调函数
③如果定义域为的函数为上高调函数,那么实数的取值范围是
其中正确的命题是 。(写出所有正确命题的序号)
15.某人午休醒来,发觉表停了,他打开收音机想收听电台整点报时,则他等待的时间短于分钟的概率为 .
16.若直角坐标平面内两点P、Q满足条件:①P、Q都在函数的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数则的“友好点对”、
有 个.
三、解答题:(本大题共6小题,满分74分.解答须写出文字说明、证明过程和演算步骤)
17.(本小题满分12分)
已知函数(),相邻两条对称轴之间的距离等于.
(Ⅰ)求的值;
(Ⅱ)当时,求函数的最大值和最小值及相应的x值.
18.(本小题满分12分)
在边长为的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(I)判别MN与平面AEF的位置关系,并给出证明;
(II)求多面体E-AFMN的体积.
19.(本小题满分12分)
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男生身高频数分布表
身高(cm) [160,165) [165,170) [170,175) [175,180) [180,185) [185,190)
频数 2 5 14 13 4 2
表2:女生身高频数分布表
身高(cm) [150,155) [155,160) [160,165) [165,170) [170,175) [175,180)
频数 1 7 12 6 3 1
(I)求该校男生的人数并完成下面频率分布直方图;
(II)估计该校学生身高在的概率;
(III)从样本中身高在180190cm之间的男生中任选2人,求至少有1人身高在185190cm之间的概率。
20.(本小题满分12分)
设函数.
(I)求的单调区间;
(II)当0
已知点为圆上的动点,且不在轴上,轴,垂足为,线段中点的轨迹为曲线,过定点任作一条与轴不垂直的直线,它与曲线交于、两点。
(I)求曲线的方程;
(II)试证明:在轴上存在定点,使得总能被轴平分
22.(本小题满分14分)
已知点列满足:,其中,又已知,.
(I)若,求的表达式;
(II)已知点B,记,且成立,试求a的取值范围;
(III)设(2)中的数列的前n项和为,试求: 。
文科数学答案
1-5BCDAB 6-10DBBAA 11—12 BC
13.62 14.②③ 15. 16.2
17.(Ⅰ).
因为 ,所以 ,. ………………… 3分
所以 .
所以 ………………………7分
(Ⅱ)
当 时, , ………………………9分
所以 当,即时,, ………………11分
当,即时,. ………………………12分
18.(1)因翻折后B、C、D重合(如图),
所以MN应是的一条中位线,………………3分
则.………6分
(2)因为平面BEF,……………8分
且,
∴,………………………………………10分
又 ∴.…………………………………12分
19.(1)样本中男生人数为40 ,
由分层抽样比例为10%可得全校男生人数为400.----2分
频率分布直方图如右图示:---------------------------------------4分
(2)由表1、表2知,样本中身高在的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的频率-----------------------------------------6分
故由估计该校学生身高在的概率.--------------------8分
(3)样本中身高在180185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:
--10分
故从样本中身高在180190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185190cm之间的可能结果数为9,因此,所求概率.---------------12分
20.(I)定义域为. ………………………1分
.
令,则,所以或. ……………………3分
因为定义域为,所以.
令,则,所以.
因为定义域为,所以. ………………………5分
所以函数的单调递增区间为,
单调递减区间为. ………………………7分
(II) ().
.
因为0
①当,即时,
在区间上,在上为减函数,在上为增函数.
所以. ………………………10分
②当,即时,在区间上为减函数.
所以.
综上所述,当时,;
当时,. ………………12分
21.(1)设为曲线上的任意一点,则点在圆上,
∴,曲线的方程为. ………………2分
(2)设点的坐标为,直线的方程为, ………………3分
代入曲线的方程,可得 ,……5分
∵,∴,
∴直线与曲线总有两个公共点.(也可根据点M在椭圆的内部得到此结论)
………………6分
设点,的坐标分别, ,则,
要使被轴平分,只要, ………………9分
即,, ………………10分
也就是,,
即,即只要 ………………12分
当时,(*)对任意的s都成立,从而总能被轴平分.
所以在x轴上存在定点,使得总能被轴平分.
22.(1)∵,,∴,
∴,∴,∴. …3分
(2)∵,∴.
∵
∴要使成立,只要,即∴为所求. ……6分
(3)∵
,∴ ……9分
∴
………………11分
∵,∴,∴…13分∴ ……14分
同课章节目录
